基于ANSYS/LS-DYNA水下钻孔爆破数值模拟
2021-10-14刘兵兵季日臣吕生玺
刘兵兵, 季日臣*, 吕生玺
(1.兰州交通大学土木工程学院, 兰州 730070; 2.甘肃省水利水电勘测设计研究院有限责任公司, 兰州 730000)
随着时代步伐的加快,爆破工程技术发展的脚步也在不断提升。目前,中国用于水下爆破最有效的方法是水下钻孔爆破技术,广泛运用于港口工程建设、航道的疏浚、水下建(构)筑物的拆除及清障等[1]。在水下爆破技术中,炮孔堵塞材料和起爆方式是决定爆破效果的重要因素。由于起爆方式的不同,爆轰波沿着装药轴线传播的时间不同,从而将对爆炸应力特征产生一定的影响,表现为岩石爆破之后产生的应力波的大小和传播方向不同,引起的振动响应也有所不同[2]。对于炮孔堵塞,其作用主要有两方面内容:①保证炮孔内炸药能够充分反应,将炸药化学能以最大程度转化为机械能;②提高炸药的热效率,将更多的热能转化为机械能,提高炸药能量的利用率[3]。所以选用合适的堵塞材料就能够降低炸药用量,有效提高爆破效果。无论是对起爆方式的研究还是对堵塞材料的研究,目前中外大多是基于露天爆破下对起爆方式和堵塞材料的模拟研究,对于该条件下水下钻孔爆破的模拟研究相对较少。高明涛等[4]运用ANSYS/LS-DYNA对水下钻孔爆破产生的地震动水压力和冲击波的传播规律进行了分析研究。王劲翔等[5]针对传统炮泥封堵易发生“冲孔”的问题,提出了以水泥浆为封堵材料,并经理论计算、数值模拟及现场实验对其合理封堵长度进行了研究。李洪伟等[6]认为采用不同起爆方式对岩石柱状装药爆破作用的影响较大,反向起爆较于正向起爆和双向起爆效果更佳。孟庆山等[7]模拟研究了珊瑚礁灰岩在三种水深情况下的单孔爆破试验,结果表明珊瑚礁灰岩的表观裂纹的数量、宽度以及爆破块度会随着水深的变化而变化,且符合Swebrec 分布函数。
虽然在应用不同堵塞材料或者不同起爆方式作用下岩石钻孔爆破的研究已取得一些成果,但同时考虑不同起爆方式和堵塞材料作用下对于水下钻孔爆破效果的研究相对较少,且该领域内的研究大多基于对实际工程的总结与分析,在理论研究及数值模拟技术等方面的研究提供的参考仍然有限。现运用ANSYS/LS-DYNA显示动力分析软件,结合不同堵塞材料研究水下岩体单点与多点起爆对炸药能量的利用及岩石破碎情况进行数值模拟,得出在该条件下对岩石爆破效果的影响。
1 数值模拟技术
1.1 计算软件的选取
近年来,利用数值模拟技术在爆破工程中取得了很多成果,建立了一些有效的数值模型,在实际工程中发挥了非常重要的作用[8]。ANSYS/LS-DYNA拥有目前世界上分析功能最齐全的显式动力分析程序包,可以利用ANSYS的仿真分析环境进行模型的建立,还可以利用ANSYS/LS-DYNA自带求解器(LS-DYNA SOLVER)进行K文件的求解,其中后处理模块可以运用专门为有限元动力仿真求解器LS-DYNA开发的后处理软件LS-Prepost进行数据分析。在爆炸分析模块,ANSYS/LS-DYNA不但能够提供相应的炸药材料模型和状态方程,还可以够模拟冲击波的传播过程和结构的瞬态响应过程[9]。因此,本文中将选取ANSYS/LS-DYNA进行模拟研究。
1.2 软件模拟过程
(1)模型建立:主要包括单元类型的选择、材料属性的定义、建立模型、网格划分、创建part、定义(对称)约束及(无反射)边界条件、能量设置、求解时间控制和输出K文件。
(2)修改K文件:在LS-Prepost中打开K文件,进行K文件的修改。主要包括材料、状态方程、单元算法、起爆初始条件、流固耦合等K文件的修改。
(3)求解:将修改好的K文件重新保存,并导入ANSYS/LS-DYNA求解器中求解,求解完成后将结果文件保存,用来记录应力、速度、加速度和变形情况以及绘制各种云图[10]。
(4)结果后处理查看:利用LS-Prepost后处理软件打开结果文件中的D3plot进行求解结果的查看。
2 模型建立
2.1 模型物理参数
若基于真实爆破情况,应考虑岩体本身属性、纹理、裂隙、断层、周边条件等多项因素的干扰,但实际分析过程不可能同时考虑到这些因素[11]。因此,在数值模拟过程中只需研究影响爆破效能的主导因素即可。因而将对本模型作如下假定与取值。
(1)水深取3 m,且只考虑水重的影响。
(2)所有材料单元均为实体单元SOLID164。
(3)为减少计算量,本文选用1/4对称模型进行模拟分析,正面和右面为对称面,设为对称边界,施加对称法向约束。
(4)将模型左、后和下边界设为无反射边界条件以模拟无限岩体和无限水域[10],水面为自由面。
(5)数值模拟单位采用cm-g-μs进行计算。
(6)考虑到整个爆破扩展持续时间,本文中模型求解时间设为2 000 μs。
模型中水体尺寸:500 cm×100 cm×300 cm(长×宽×高),岩体尺寸:500 cm×100 cm×400 cm;炮孔为高300 cm,直径10 cm的长方体。模拟时采用连续装药,上部堵塞段50 cm,炸药装填深度为250 cm。
2.2 材料参数及算法
本文中主要材料有:岩石、炸药、水和炮泥。其中岩石和泡泥采用Lagrange算法,炸药和水采用ALE算法。模型计算采用多物质ALE流固耦合算法,使得网格不致出现严重的畸变[12]。
在本模型中岩体和炮泥均采用各向同性双线性弹塑性模型(*MAT_PLASTIC_KINEMATIC),主要参数[13]见表1。

表1 岩石材料参数Table 1 Rock material parameters
炸药参数采用乳化炸药参数,模型为高能炸药材料模型(*MAT_HIGH_EX-PLOSIVE_BURN),状态方程用JWL (Jone-Wilkins-Lee)物态方程[14]进行描述,状态方程表达式[15]为
(1)
式(1)中:E0为初始内能密度;P为压力;V为相对体积;A、B、R1、R2、ω均为材料常数。炸药材料及状态方程参数[13]见表2。

表2 炸药材料及状态方程参数Table 2 Explosive materials and state equation parameters
水材料模型用ANSYS/LS-DYNA自带的材料本构模型(*MAT_NULL),状态方程用Gruneisen进行描述[16]为
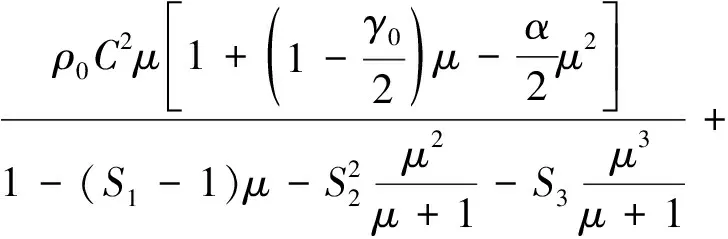
(γ0+αμ)E0
(2)
式(2)中:ρ0为材料初始密度;C为剪切-压缩波速曲线截距;μ为动力黏滞系数,μ=ρ/ρ0-1;γ0为常数;α为体积修正量;S1、S2、S3为常数。水材料及状态方程参数见表3。

表3 水材料及状态方程参数Table 3 Water material and state equation parameters
2.3 计算工况
本文中讨论在同一水深条件下,不同堵塞材料及不同起爆点作用下水下岩石爆破数值模拟,分为以下3种工况6种情况进行模拟,模型示意图如图1所示。
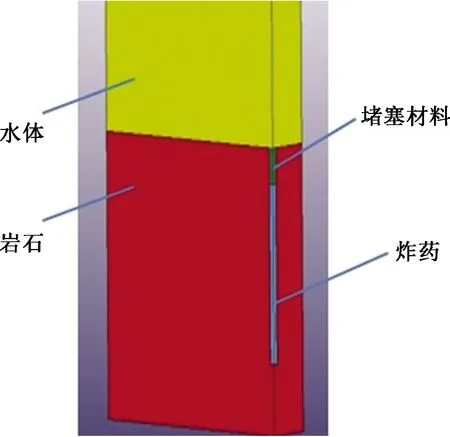
图1 模型示意图Fig.1 Schematic diagram of the model
工况一:炸药中心起爆(水和炮泥堵塞);
工况二:炸药两端同时起爆(水和炮泥堵塞);
工况三:炸药顶端、中心和底端同时起爆(水和炮泥堵塞)。
3 模拟结果及分析
3.1 平行炮轴线单元应力分析
分别在近堵塞段、装药段中部、装药段底部选取1325号、590号和2号单元,在岩-水接触面选取1435号单元,其具体位置如图2所示。分析在3种起爆方式下水和炮泥堵塞时1325号、590号和2号单元的压力时程曲线图,如图2所示。
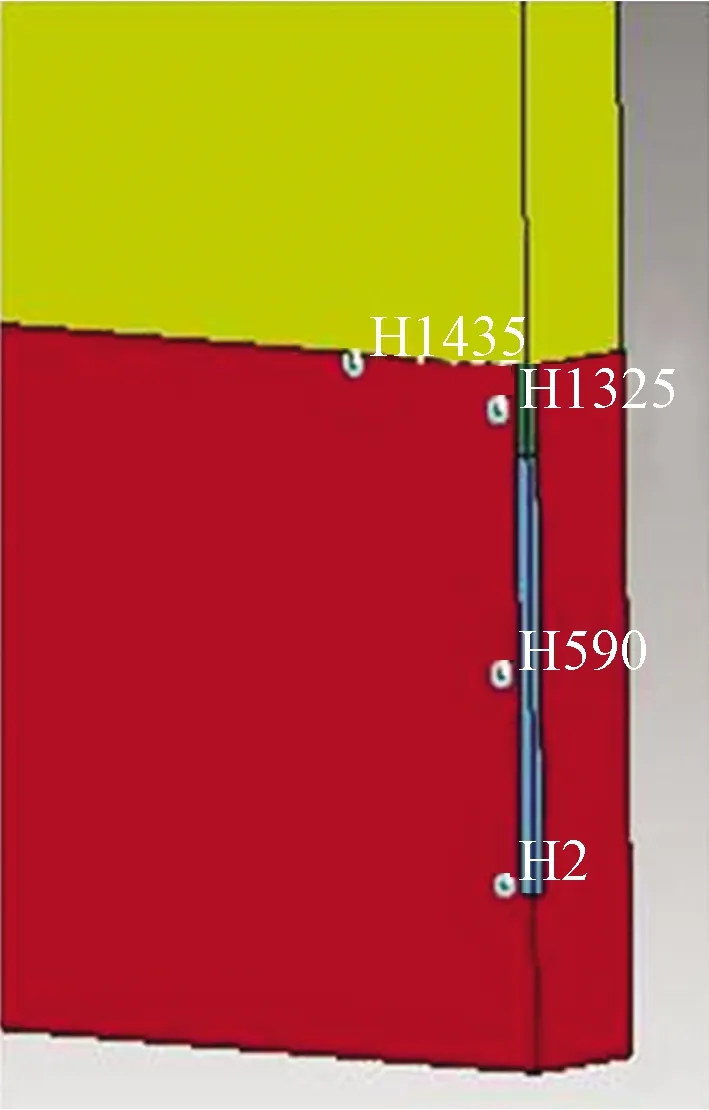
图2 爆破取样点位置示意图Fig.2 Schematic diagram of the location of blasting sampling points
如图3所示,对于中心起爆,水材料堵塞下A单元在418 μs达到拉应力峰值535 MPa,B单元在159 μs达到拉应力峰值135 MPa,C单元在376 μs达到拉应力峰值445 MPa;炮泥堵塞下A单元在418 μs达到拉应力峰值619 MPa,B单元在159 μs达到拉应力峰值135 MPa,C单元在376 μs达到拉应力峰值445 MPa。可以看出,中心起爆条件下,在堵塞段附近,炮泥堵塞对于岩石的爆破效果更佳。

图3 中心起爆各单元压力时程曲线图Fig.3 Pressure time history curve diagram of each unit of central detonation
如图4所示,对于两端同时起爆,水材料堵塞下A单元在674 μs达到拉应力峰值236 MPa,B单元在374 μs达到拉应力峰值878 MPa,C单元在619 μs达到拉应力峰值206 MPa;炮泥堵塞下A单元在674 μs达到拉应力峰值201 MPa,B单元在374 μs达到拉应力峰值881 MPa,C单元在609 μs达到拉应力峰值204 MPa。可以看出,两端起爆条件下,各单元拉应力峰值基本一致,堵塞段附近水封条件下爆破效果稍佳,其他部位水堵塞与炮泥堵塞条件下爆破效果基本相同。
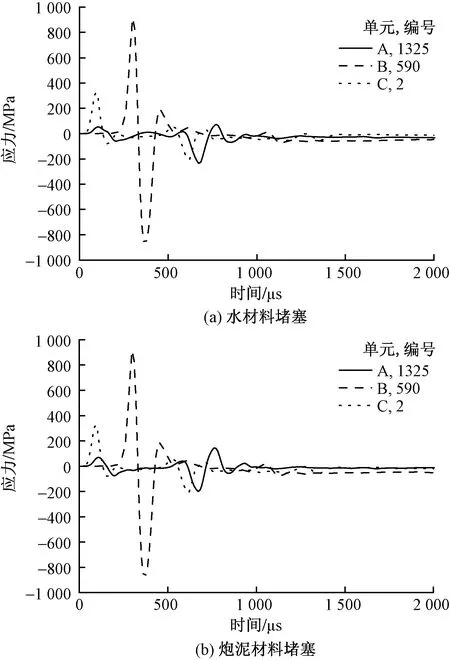
图4 炸药两端同时起爆各单元压力时程曲线图Fig.4 The pressure time history curve of each unit initiating the explosive at both ends simultaneously
如图5所示,对于三点同时起爆,水材料堵塞下A单元在407 μs达到拉应力峰值187 MPa,B单元在353 μs达到拉应力峰值513 MPa,C单元在342 μs达到拉应力峰值260 MPa;炮泥堵塞下A单元在407 μs达到拉应力峰值213 MPa,B单元在353 μs达到拉应力峰值514 MPa,C单元在342 μs达到拉应力峰值260 MPa。可以看出,三点同时起爆条件下,各单元拉应力峰值差距不大,堵塞段附近炮泥堵塞条件下爆破效果稍佳,其他部位水堵塞与炮泥堵塞条件下爆破效果基本相同。
如图3~图5所示,在同一堵塞材料作用下,相对于两端起爆和三点起爆,炸药中心起爆对岩石的爆破效果更佳。但在炸药中心附近岩石,由于应力波的叠加作用,两端起爆和三点起爆爆破效果明显比中心起爆效果更好。
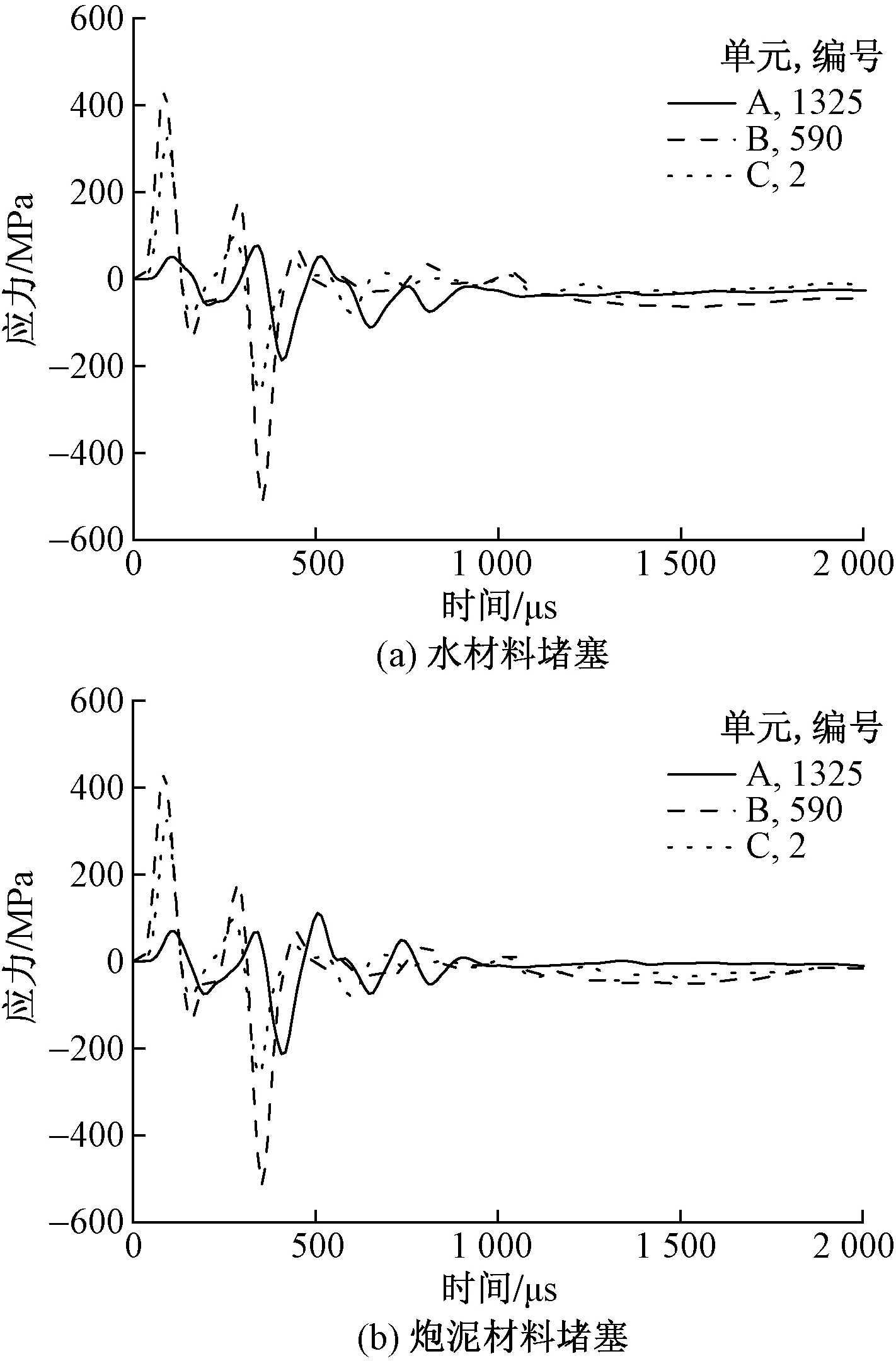
图5 三点同时起爆各单元压力时程曲线图Fig.5 Three-point simultaneous detonation pressure time history curve of each unit
3.2 节点速度分析
为分析考虑水体作用下岩石爆破后波速的变化情况,在炸药上部岩-水接触面分别取8305号、8312和8319号节点,其具体位置如图6所示。分析在三种起爆方式下(水和炮泥堵塞)各点的速度时程曲线图,如图7~图9所示。

图6 取样节点位置示意图Fig.6 Schematic diagram of sampling node location
如图7所示,炸药中心起爆,水材料堵塞下A、B、C三点速度峰值分别为36.9、14.4、7.77 m/s;炮泥材料堵塞下A、B、C三点速度峰值分别为45.5、15.2、7.77 m/s,说明在炮泥堵塞下,炸药能量更能够充分反应,提高了能量利用率。
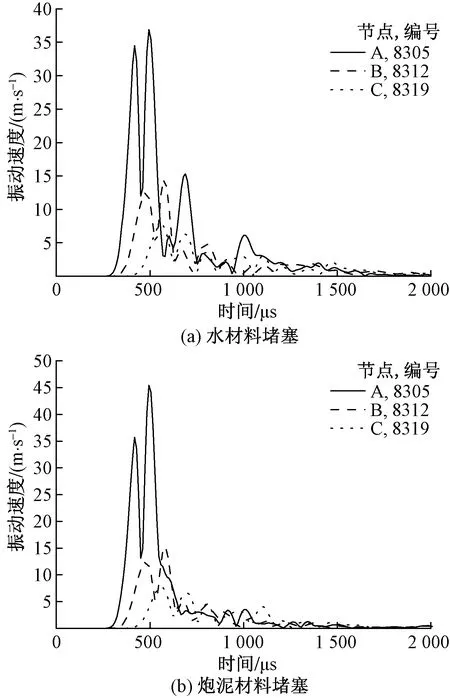
图7 中心起爆各点速度时程曲线图Fig.7 Time history curve of velocity at each point of central detonation
如图8所示,炸药两端同时起爆,水材料堵塞下A、B、C三点速度峰值分别为20.8、15.0、11.7 m/s;炮泥材料堵塞下A、B、C三点速度峰值分别为21.3、15.1、11.2 m/s。说明两端同时起爆下,水材料堵塞比炮泥堵塞作用下对炸药能量的利用略有优势。
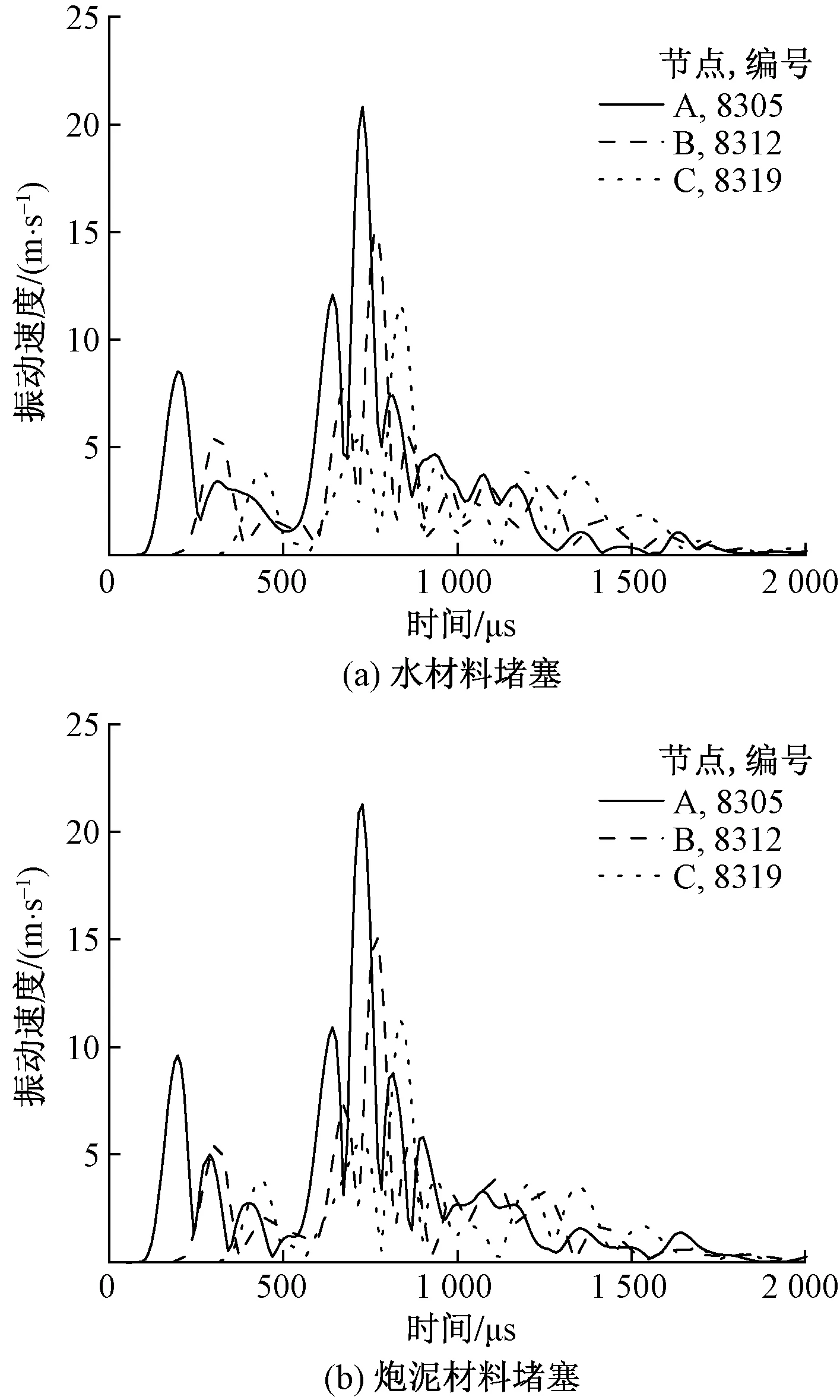
图8 炸药两端同时起爆各点速度时程曲线图Fig.8 Time-history curve of velocity at each point of explosive detonation at both ends simultaneously
如图9所示,三点同时起爆,水材料堵塞下A、B、C三点速度峰值分别为18.3、12.8、7.86 m/s;炮泥材料堵塞下A、B、C三点速度峰值分别为21.1、12.4、7.73 m/s。说明三点同时起爆下,炮泥堵塞作用下炸药能量利用效果稍优于水材料堵塞。
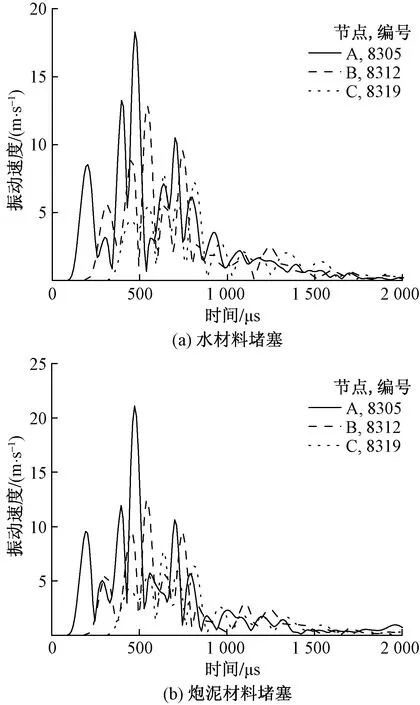
图9 三点同时起爆各点速度时程曲线图Fig.9 Three-point simultaneous detonation speed time history curve diagram of each point
由图7~图9可知,在同一堵塞材料下,中心起爆振动速度峰值大于两端起爆和三点起爆,且随着距离炮孔距离的增大不断衰减,最终慢慢趋于一致。说明在同一堵塞材料堵塞下,整体情况中心起爆对炸药能量的利用较两端起爆和三点起爆更为充分。
3.3 药包上侧岩-水接触面单元应力分析
选取药包上侧岩-水接触面1435号单元分析其竖向应力变化情况。具体位置如图1所示。
图10所示曲线图分别为在水封条件和炮泥堵塞条件下三种起爆方式时药包上侧岩体和水体交接处单元的应力时间曲线图,在爆破过程中,岩体的受力首先从压缩变为拉伸,然后又从拉伸变为压缩状态,又转变成为拉伸状态,最后一直在一个相对稳定的数值上下波动。起始状态的压缩应力波在传播至岩-水交接面时,由于水体的作用产生了反射应力波,从而使得药包上方局部区域岩体内的应力状况产生较大变化,较大程度提升了岩体的破坏程度。
如图10可知,在水材料和炮泥堵塞情况下,前期中心起爆和三点起爆使得岩体爆破产生的应力波动较大,但在整个爆破过程中,两端起爆使得岩体爆破产生的应力扰动较为均匀,且持续性强,因而整体爆破效果好。
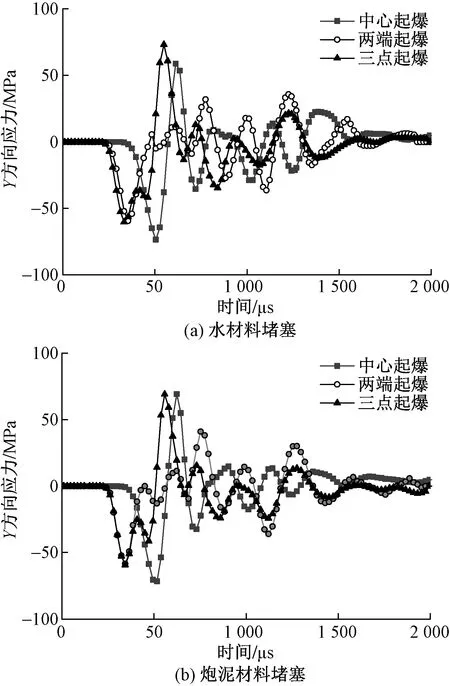
图10 药包上侧岩-水接触面单元应力时间历时曲线图Fig.10 Stress time duration curve of the upper side rock-water contact surface of the medicine packet
4 结论
(1)在同一起爆方式下,不同堵塞材料对水下岩体爆破效果不同,而且不同部位其爆破效果也有差异。而在同一堵塞材料作用下,相对于两端起爆和三点起爆,炸药中心起爆对岩石的爆破效果更佳。
(2)在不同起爆方式、不同堵塞材下岩石爆破对炸药的能量利用情况不同。炸药中心起爆和三点起爆,炮泥堵塞具有较高的爆炸能量利用率;两端起爆,水材料堵塞对炸药能量的利用率较高。
(3)在岩-水接触面位置,水材料和炮泥材料对于岩石的爆破效果的影响并不明显,两种堵塞方式下两端起爆相对于岩石的爆破效果更好。
