基于FBCREAM方法的飞机驾驶人因可靠性评估模型

郭云东， 孙有朝

(南京航空航天大学民航学院， 南京 210016)

随着先进航空电子技术的不断涌现和机载设备可靠性的提高，与飞机机电系统有关的航空事故发生率在最近几十年已急剧下降[1]。但是，与人为差错相关的航空不安全事件/事故发生率尚未得到很好的控制。国际民用航空组织的事故统计数据表明，超过70%的不安全事件/事故与人为差错直接或间接相关[2-3]。因此，复杂飞行任务中飞行员的人因可靠性评估(human reliability assessment, HRA)对于识别关键人为差错，提高飞行安全至关重要。HRA是一种用于量化人因可靠性的工具，其主要目的是通过预测人为差错概率和评估人为差错对人机系统的退化来确定操作员对系统可靠性的影响[4]。

目前，研究学者们已开发出多种HRA方法，主要包括第一代HRA和第二代HRA[5-6]。20世纪70年代末至90年代初的第一代HRA方法将人视作像机械、电气或结构部件一样具有固有的失效概率，其中THERP (technique of human error rate prediction)是最具代表性的方法之一，该方法在核电、轨道交通等领域广泛应用[7-8]，但第一代HRA没有考虑到外界情境环境的影响以及人的认知特性，如感知、判断、决策等。20世纪90年代末至今的第二代HRA方法认为情境环境是影响人的绩效的关键因素，结合人的认知过程，建立了环境与人为差错之间的关系模型[9]。典型的第二代HRA方法有ATHEANA (a technique for human error analysis)和CREAM (cognitive reliability and error analysis method)[10]，其中，ATHEANA主要应用于核电领域，而CREAM方法已在航空、航天、海事、地面交通、核电等领域得到了广泛应用。例如，罗凤娥等[11]考虑到陆空通话影响签派员和飞行员之间的沟通和交流，对CREAM方法中给出的认知行为和认知功能进行了改进，用于确定签派员与飞行员间的人因可靠性。裴立冠等[12]通过优化人为差错形成因素(error shaping factor，ESF)的水平等级，改进人为差错形成条件因子依赖规则，量化飞行员的人因可靠性。Calhoun等[13]考虑了航天飞行的极其复杂性并改进了人为差错形成条件，根据人为差错形成条件的状态不同为每个ESF分配一个权重因子，从而计算航天员的人因可靠性。王彦富等[14]引入模糊推理对ESF进行模糊评价，结合多元线性回归方法建立ESF与控制模式间的对应关系，实现了海洋平台作业的人因可靠性量化。李蒙等[15]提出了CREAM与灰色关联相结合的方法，用于评估导致核电厂人因失误的因素，并根据关联度对这些因素进行排序，识别出与人因失误关联度较大的因素。虽然上述方法在各自领域得到了较好应用，但是这些方法没有考虑人为差错形成条件的不确定性以及人为差错模式的不确定性，且飞机驾驶的情境环境不同于航海、航天、核电工业等，因此，它们不能直接应用于飞机驾驶人因可靠性评估。

为解决飞机驾驶人机交互过程中人为差错形成条件的不确定性以及人为差错模式的不确定性问题，现提出一种基于FBCREAM(fuzzy Bayesian CREAM)方法的飞机驾驶人因可靠性评估模型。首先，对原始CREAM方法中给出的人为差错形成条件进行改进优化，使其更符合实际飞行情境。其次，针对人为差错形成条件的不确定性以及人为差错模式的不确定性问题，引入模糊逻辑方法对人为差错形成条件进行模糊化处理，将其作为贝叶斯网络的输入参数，通过贝叶斯网络模型推理和重心法解模糊化技术，计算得出人为差错概率精确值，为航空安全评估提供支持。

1 基于FBCREAM的飞机驾驶人因可靠性评估模型

1.1 CREAM方法

1.1.1 人为差错形成条件

为核电厂概率安全评估开发的原始CREAM方法定义了九个绩效影响因素，也称作人为差错形成条件，用于描述操作员发生错误行为的原因[16]。这些人为差错形成条件包括：组织的充分性、人机界面的充分性、工作条件、程序的可用性、同时目标的数量、可用时间、工作时间(白天或者夜晚)、训练/经验和团队协作质量。然而，飞机驾驶情境环境显然不同于核电厂情境环境，尤其是长时间飞行和陆空通信等地面支持的情境因素。在长时间飞行中，每个飞行员必须熟悉各种飞行状况信息，如飞机状态、故障预定信息、备用机场、机场天气和航线等。在长时程飞行的每个阶段，飞行员需要在合适时间内准确执行大量的操作程序。与此同时，机组人员必须通过无线通信与地面的空中交通管制员进行定期通信，以确保飞行安全。这些烦琐的操作给飞行的生理和心理都带来了极大的挑战，可能会进一步影响飞行员的表现，甚至导致人为差错。因此，基于原始CREAM方法给出的ESF，结合飞机驾驶情境环境特点，通过航空事故分析和专家分析判断，从人-机-环系统角度出发提出一组合理的ESF用于描述飞行情境环境中飞机驾驶人为差错形成条件，如表1所示。每个ESF涉及3个状态水平，即高、中、低。其中，ESF1～ESF6从低到高的状态水平对飞行员效能的影响分别为降低、正常、提升；为了便于统一表述，ESF7、ESF8分别为负任务负荷、负认知压力，表示负任务负荷和负认知压力越高，越提升飞行员效能的影响。

表1 人为差错形成条件及对飞行员效能的影响

1.1.2 人为差错模式

在上述ESF共同作用下，飞行员可能出现不同差错模式。引入原始CREAM方法中反映人的可靠性状态的四种控制模式，即人为差错模式，包括战略模式、战术模式、机会模式和错乱模式[16]。战略控制模式是指操作员有足够的时间来考虑整个情况并做出相应的计划；战术控制模式是指操作员按照标准程序或规则执行任务计划；机会控制模式是指下一步行动取决于当前环境特征，而不是取决于更稳定的意图或目标，操作员很少做计划或预期，可能是因为没有清楚理解情境环境，或是因为时间非常有限；错乱控制模式是指操作员对当前的情况不熟悉，在任务需求非常高的情况下失去态势感知。每个控制模式都有相应的人为差错概率(human error reliability，HEP)区间，具体如表2所示。

表2 人为差错模式及其取值范围

1.1.3 人为差错形成条件与人为差错模式映射关系

原始CREAM方法中给出了9个ESF与4个人为差错模式的映射关系，然而本文只有8个ESF，因此需要对其进行调整，图1展示了调整后的飞机驾驶人为差错形成条件与人为差错模式的映射关系，x轴表示降低人绩效的ESF数量之和，y轴表示提升人绩效的ESF数量之和。每个ESF有三个状态水平，对飞行员效能的影响分别是提升、正常、降低，假定降低人的绩效的ESF数量之和为i，提升人的绩效的ESF数量之和为j，则通过元组(i,j)(i,j=0,1,…,8)可确定飞行员的人为差错模式，且i与j的组合共有45种，如图1所示。例如，在飞机单发失效情境环境下，假定有6个ESF会降低飞行员操作效能，2个ESF会提升飞行员操作效能，则(x,y)=(6,2)表明飞行员的人为差错模式为机会型控制模式，且人为差错概率值落在区间(1×10-2,5×10-1)。

图1 人为差错形成条件与人为差错模式映射关系Fig.1 Mapping relation between human error shaping factor and human error mode

1.2 模糊逻辑

1.2.1 模糊化

模糊化是将一个系统的输入变量分解成一个或多个模糊集，从而产生多个输入的模糊感知数。模糊数是一个凸模糊集，其特征是在给定的实数区间，每个区间的隶属度在0～1之间。8个ESF的定性描述高(提升)、中(正常)、低(降低)对应的取值范围如表1所示，人为差错模式定性描述及对应的概率区间如表2所示，选取三角形隶属函数与梯形隶属函数，构建人为差错形成条件和人为差错模式的隶属函数，结果如图2所示。为了便于图形化显示人为差错模式区间范围值采用了对数运算处理。将每个ESF不同状态水平的隶属度作为贝叶斯网络的输入，通过贝叶斯网络模型得出四种人为差错模式的隶属度。

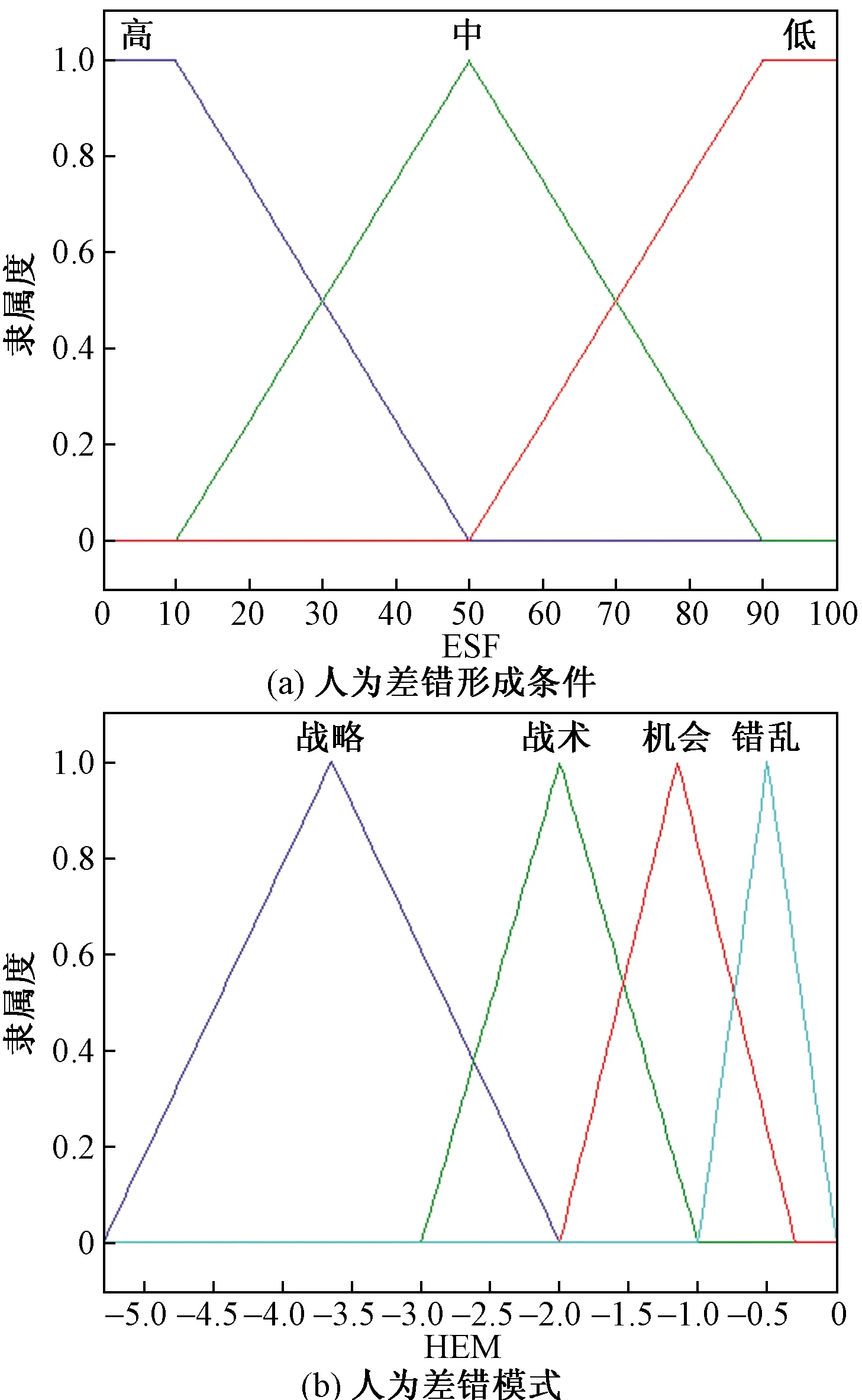
图2 人为差错形成条件与人为差错模式的隶属函数Fig.2 Membership function of human error shaping factor and human error mode

其中，人为差错形成条件的隶属函数表达式为

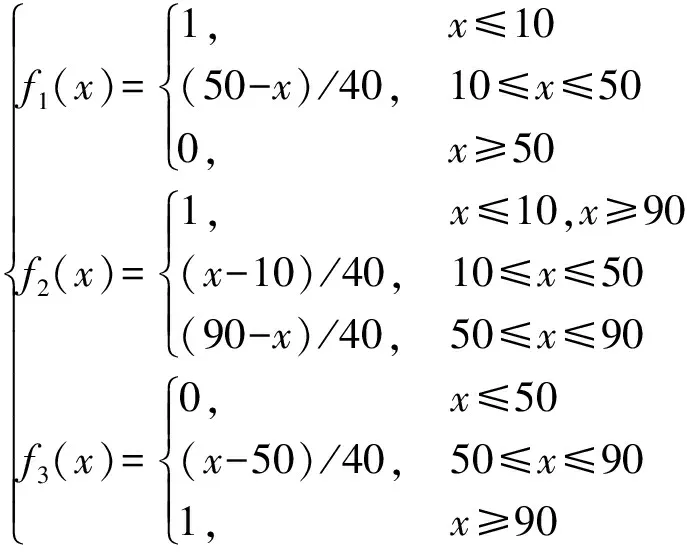
(1)

人为差错模式的隶属函数表达式为

(2)

2.2.2 解模糊化

解模糊化就是将模糊输出转化为精确值。目前研究学者已开发出多种解模糊化方法，如最大隶属度法、重心法和加权平均法等[17]。选择相对准确的重心法计算精确值，具体表达式为

(3)

式(3)中：CV为精确值；f(x)=f战略(x)+f战术(x)+f机会(x)+f错乱(x)。

则人为差错概率HEP的计算表达式为

HEP=10CV

(4)

1.3 贝叶斯网络

原始CREAM方法是一种简单且易于使用的人为差错概率评估方法，但原始CREAM方法主要缺陷是没有考虑人为差错形成条件的不确定性和人为差错模式的不确定性。为了解决原始CREAM法的局限性，引入贝叶斯网络将这些不确定性反映到网络中，通过贝叶斯网络推理得到飞机驾驶人为差错模式的隶属度，将其用于解模糊化分析。基于人为差错形成条件与人为差错模式的关系构造贝叶斯网络，如图3所示。

图3 人为差错模式贝叶斯网络Fig.3 Bayesian network of human error mode

图3中第一层是8个ESF，也是贝叶斯网络的输入层，可以通过模糊逻辑方法计算得到。每个ESF有3个状态水平，对飞行员效能有三种影响，共有8个ESF，那么有38=6 561个可能状态，然而，过多状态会导致计算过于复杂。因此，将8个ESF分为3组：组织管理类、环境类、工作负荷类，以此降低计算复杂性。其中属于组织管理类的人为差错形成条件包括ESF1(陆空通信)、ESF2(机组资源管理)、ESF3(组织充分性)、ESF4(机组训练/经验)；属于环境类的人为差错形成条件包括ESF5(人机界面性能)、ESF6(驾驶舱环境)；属于工作负荷类的人为差错形成条件包括ESF7(负任务负荷)、ESF8(负认知压力)。第三层是人为差错模式，也是网络的输出层。

2 实例分析

为了验证本文模型在飞机驾驶人为差错概率评估的适用性，选择了单发故障情境下的飞行任务进行实验研究。

2.1 实验及数据

本文实验在南京航空航天大学人机工效与适航技术研究中心进行，以研究中心搭建的飞行模拟器为实验平台，选取6名南京航空航天大学民航学院/飞行学院的飞行学员作为被试人员。6名飞行学员被邀请在飞行模拟器上进行单发故障情境下飞行任务执行实验，任务结束后需要对8个ESF进行自我评估并填写ESF问卷，从0～100进行打分，分值越高该ESF负面影响越大。为了尽量减少未知因素影响，每天9:00—11:00邀请两名飞行学员进行实验，实验进行3 d，实验过程如图4所示。表3为记录的实验结果，根据获取的实验结果，通过8个ESF的隶属函数计算每个ESF的隶属度，并将其作为构建的贝叶斯网络模型的输入参数。

2.2 人为差错概率评估

由于使用了6名飞行学员进行实验，且每个人的人为差错模式隶属度及HEP计算过程是类似的，本部分仅以飞行学员1的实验为例进行计算演示。基于构建的人为差错形成条件隶属函数计算每个ESF隶属度，结果如表4所示，结合建立的贝叶斯网络模型(图3)，计算得出飞行学员1的人为差错模式隶属度，如图5所示。

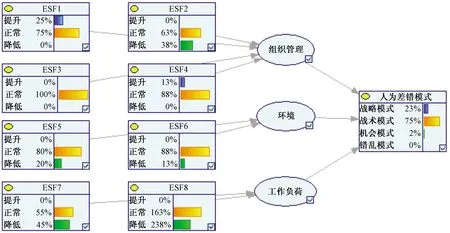
图5 飞行学员1的贝叶斯网络推理结果Fig.5 Reasoning result of No.1 pilot cadet

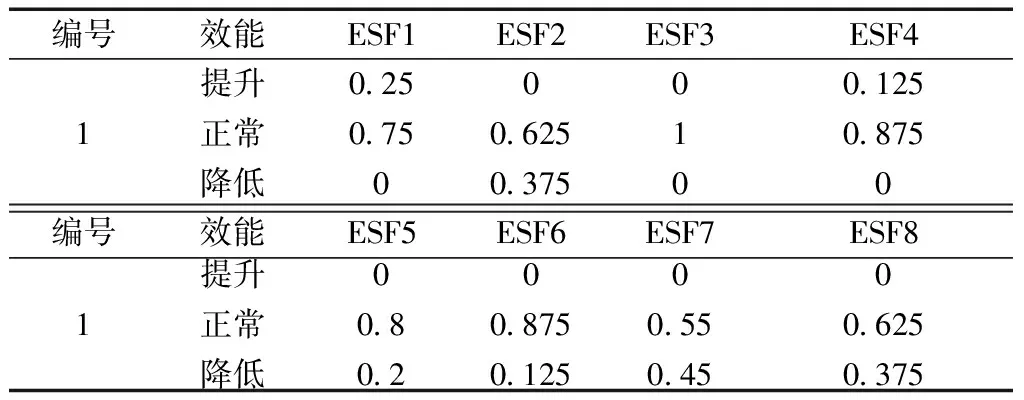
表4 飞行学员1的人为差错形成条件隶属度

由图5可知，飞行学员1的人为差错模式的隶属度为(0.23, 0.75, 0.02, 0)，结合式(2)～式(4)，通过重心法解模糊化计算输出的精确值CV，进而求得飞行学员1的HEP，具体计算过程为

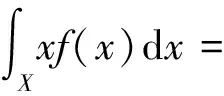
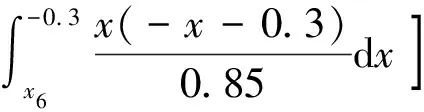
(5)

(6)

(7)

HEP=10CV=3.14×10-3

(8)

类似地，通过上述方法依次计算求得其他5名飞行学员的人为差错概率，最终结果如表5所示。

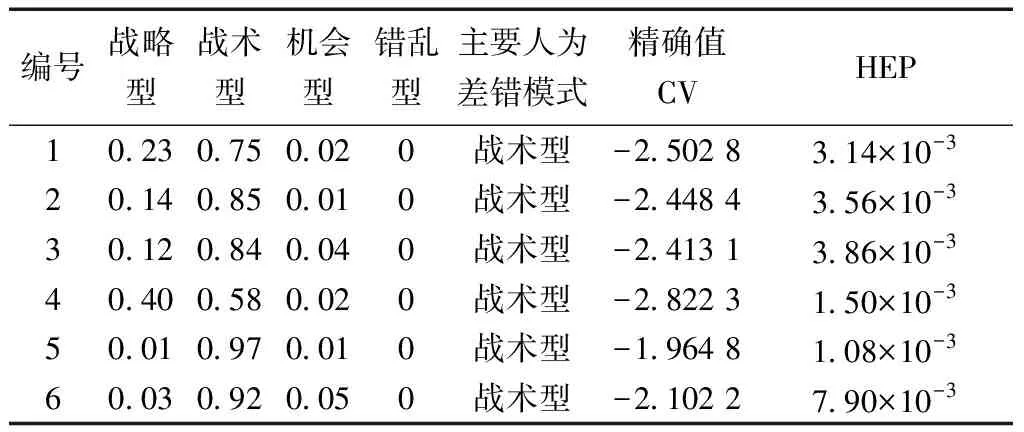
表5 被试飞行学员的人为差错模式隶属度及HEP

2.3 结果讨论

飞行学员的人为差错模式隶属度及HEP结果表明飞行学员的主要人为差错模式均为战术型控制模式，这意味着他们是根据飞行程序或计划有序地进行任务操作。飞行学员4的人为差错概率为1.50×10-3，是所有飞行学员中的最低值，表明飞行学员4在飞行学习过程中较好地掌握了飞行知识和操作技能，针对事故情境下的飞行任务处理能力也要高于其他被试飞行学员。相反，飞行学员5的操作绩效表现最差，其人为差错概率为1.08×10-2，是所有被试人员中发生差错概率最高的人员，表明该飞行学员较为缺乏非正常事件应对操作的经验，需加强在特殊情况下的应急反应和操作技能训练。飞行学员1、2、3的人为差错模式隶属度比较接近，因此，针对此三人求得的精确值和人为差错概率也很接近，可以用于检验模型的灵敏性。飞行学员6相比于飞行学员1、2、3也具有较高的人为差错概率，其人为差错模式隶属度与飞行学员5类似，表明该飞行学员在单发故障情境下的飞行任务操作能力仍有不足，在处理突发事件情境下具有较高的任务负荷与认知压力，需进一步提升自身的认知能力，积累更多飞行经验。

基于原始CREAM方法的观点，本次实验的6名飞行学员的操作绩效均处于可接受且适当的区域，通过模糊逻辑和贝叶斯网络建模方法得出的结果落在原始CREAM给出的概率区间范围内，验证了本模型在飞机驾驶人为差错评估的适用性与合理性。同时，改进后的飞机驾驶人为差错评估模型较原始CREAM方法能够更加精确计算人为误差概率值，为事件树或故障树分析等其他定量航空安全风险评估提供了确定值。

3 结论

(1)提出了一种基于FBCREAM方法的飞机驾驶人为差错评估模型，用于量化飞行任务执行过程中的飞行员人因可靠性。

(2)考虑到飞机驾驶的特殊情境环境，改进了原始CREAM方法中的人为差错形成条件，使其更加真实地反映飞机驾驶舱中飞行员的人因特点和任务情境环境。引入模糊逻辑方法来构建人为差错形成条件和人为差错模式的隶属函数，并将每个ESF不同状态水平的隶属度作为贝叶斯网络模型的输入参数，通过贝叶斯网络推理计算获得不同人为差错模式的隶属度，结合解模糊化方法求得人为差错概率。选取了单发故障情境下飞行员任务操作进行了实验研究，结果表明本次被试飞行学员的人因可靠性基本上是可以接受的且符合实际情况，他们的主要人为差错模式是战术型控制方式，与原始CREAM给出的概率区间相比，得到的结果是令人满意的，并且在预期范围内。

(3)所提出的方法和模型可应用于航空安全风险评估领域，为减少人为差错，确保飞行安全提供了重要支持。