七人表决逻辑电路的设计与实现

孙宇舸，叶 柠，李景宏

（东北大学 信息科学与工程学院，辽宁 沈阳 110819）

表决逻辑在实际生活中具有广泛的应用。如何设计表决逻辑电路是组合逻辑电路的重要研究内容。

在大部分表决逻辑电路的分析与设计中，通常都是以三人表决逻辑电路的设计[1-4]为例来说明组合逻辑电路的设计方法，很少涉及五人以上的表决逻辑电路的设计。因为当逻辑变量个数较多时，输入输出的逻辑关系以及逻辑函数的化简和电路设计都比较复杂。但是在实际的生产和生活当中，多人表决逻辑具有广泛的需求[5]，本文就是以七人表决逻辑电路设计为例，说明多人表决逻辑的设计方法和电路实现。

本文主要研究了七变量的表决电路的逻辑关系，提出了简易的七变量表决逻辑卡诺图的化简方法，将原本复杂而庞大的七变量卡诺图分解为4个四变量卡诺图，实现化繁为简，从而得出七人表决逻辑的逻辑函数表达式，通过对逻辑函数表达式的分析与变换，通过数据选择器进一步简化电路，实现了七人表决逻辑电路的设计。

1 设计方法

表决逻辑电路是根据输入状态决定输出状态，因此属于组合逻辑电路。组合逻辑电路的设计步骤[6]如图1所示。

图1 组合逻辑电路的设计步骤

1.1 基于逻辑功能的描述，分析事件的因果关系，确定电路的输入逻辑变量和输出逻辑变量

通常把事件的起因定义为输入逻辑变量，事件的结果定义为输出逻辑变量，并用二值逻辑的0和1对输入和输出变量进行逻辑赋值[5]。

七人表决逻辑的逻辑功能为：由七人投票决定决议是否通过。当多数人投票同意时，即同意人数大于等于4人时，表示决议通过；当同意人数小于4人时，表示决议不被通过。因此该电路输入变量为7个，即参与投票的7人，分别用字母A、B、C、D、E、F、G表示，“同意”定义为1，“不同意”定义为0。输出变量表示决议是否被通过，用字母Y表示，“通过”定义为1，“不通过”定义为0。

1.2 由文字描述的逻辑功能的因果关系，列出真值表或卡诺图

卡诺图（Karnaugh map）是数字逻辑电路设计中的一种常用数学工具，是逻辑函数的一种图形化表示方法，和真值表一样可以表示逻辑函数和输入逻辑变量之间的逻辑关系，与真值表具有一一对应的关系，可以看做是真值表的一种变形。画卡诺图时，需要注意要将逻辑上相邻的最小项变成几何位置上相邻的方格图，做到逻辑相邻和几何相邻的一致性[6]。

在七人表决逻辑中，由于输入变量为7个，因此输入变量的取值组合一共有27=128种，可见无论是七变量的真值表还是卡诺图都会相当复杂，因此本文针对表决逻辑，提出一种将七变量卡诺图转换为4个四变量卡诺图的方法。

将三个输入变量E、F、G单独考虑，则可以将七人表决逻辑功能分为四种情况：

（1）当EFG三个变量都为0时，即EFG=000，则A、B、C、D四个变量都为1时，输出Y=1，其他取值组合输出Y=0，对应的卡诺图如图2所示。

图2 七人表决逻辑卡诺图（EFG=000）

（2）当EFG三个变量中有一个变量为1时，即EFG=001/010/100时，则A、B、C、D四个变量中至少有三个变量为1时，输出Y=1，其他取值组合输出Y=0，对应的卡诺图如图3所示。

图3 七人表决逻辑卡诺图（EFG=001/010/100）

（3）当EFG三个变量中有两个变量为1时，即EFG=011/101/110，则A、B、C、D四个变量至少有两个变量为1时，输出Y=1，其他取值组合输出Y=0，对应的卡诺图如图4所示。

图4 七人表决逻辑卡诺图（EFG=011/101/110）

（4）当EFG三个变量都为1时，即EFG=111时，则A、B、C、D四个变量中至少有一个变量为1时，输出Y=1，其他取值组合输出Y=0，对应的卡诺图如图5所示。

图5 七人表决逻辑卡诺图（EFG=111）

1.3 化简卡诺图，获得最简逻辑函数表达式

由于卡诺图用几何位置的相邻表示了构成函数的各个最小项在逻辑上的相邻性，因此可以方便地求出逻辑函数的最简与或式，进而实现逻辑电路。

卡诺图化简逻辑函数的基本原则[7]为：

（1）圈1方格得逻辑原函数，圈0方格得逻辑反函数。

（2）包围圈必须覆盖所有的1方格。

（3）包围圈中1的个数必须是2n个相邻的1。

（4）包围圈的个数必须最少（乘积项最少）。

（5）包围圈越大越好（消去的变量多）。

（6）每个包围圈至少包含一个新的最小项。

根据上述原则，分别对图2-图5的卡诺图进行化简，具体的包围圈的画法如图中所示：

（1）当EFG三个变量都为0时，化简图2卡诺图的包围圈，得逻辑函数表达式为：

（2）当EFG三个变量中有一个变量为1时，化简图3卡诺图的包围圈，得逻辑函数表达式为：

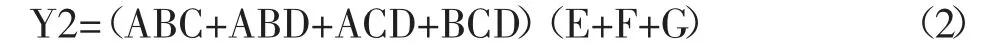
（ABC+ABD+ACD+BCD）（E'F'G+E'FG'+EF'G'）。

（3）当EFG三个变量中有两个变量为1时，化简图4卡诺图的包围圈，得逻辑函数表达式为：

（4）当EFG三个变量都为1时，化简图5卡诺图的包围圈，得逻辑函数表达式为：

综上所述，则七人表决逻辑的最简逻辑函数的与或表达式为：

基于七人表决逻辑的逻辑功能描述，当大于等于4人同意时，决议通过，按照排列组合的方法可以确定一共有C74=35种组合，在逻辑函数表达式（5）中，逻辑函数为35个与项的或，与分析一致。

1.4 由化简后的逻辑函数表达式画出逻辑图

逻辑图是利用逻辑门来完成逻辑功能的电路图。基于逻辑函数表达式（5），利用35个8输入与门，4个8输入或门，1个3输入或门和1个5输入或门即可实现七人表决逻辑的逻辑函数，基于基本逻辑门的七人表决逻辑的逻辑图如图6所示。

图6 基于基本逻辑门的七人表决逻辑的逻辑图

2 基于数据选择器的电路设计与实现

由图6可以看出，基于基本逻辑门实现的七人表决逻辑电路需要使用41个不同输入变量的基本逻辑门，逻辑门数量众多，电路复杂，可考虑进一步对电路进行简化。

逻辑函数表达式（5）可以改写为：

+（A+B+C+D+C）EFG。

根据八选一数据选择器的逻辑函数：

将EFG三个变量看做八选一数据选择器的地址输入端A2A1A0，则有：

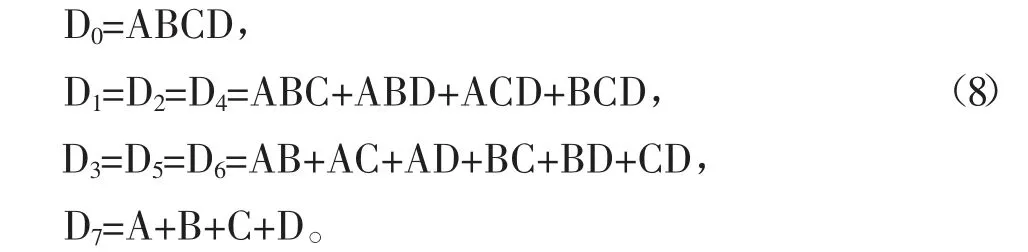
由此基于八选一数据选择器74LS151实现的七人表决逻辑电路的电路图如图7所示。

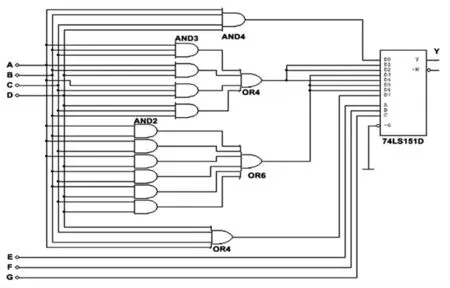
图7 基于数据选择器的七人表决逻辑电路图

采用数据选择器将大大减少基本逻辑门的数量，大大简化了电路结构，使电路更为稳定并具有一定的可扩展性。

3 结束语

本文研究了数字逻辑电路中的七人表决逻辑电路的设计方法，提出了基于表决逻辑的多变量卡诺图的化简方法，分别采用基本逻辑门电路和数据选择器两种方式实现了七人表决逻辑电路。文章的研究方法可向多变量表决逻辑电路扩展，为组合逻辑电路的分析与设计提供了新思路。