大跨度铁路悬索桥模态参数研究

郭 辉,胡所亭,董振升,韦庆冬,金 花,苏朋飞

(1.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081； 2.高速铁路轨道技术国家重点实验室,北京 100081；3.中国铁道科学研究院集团有限公司,北京 100081； 4.中国铁路上海局集团有限公司,上海 200071)

引言

悬索桥的模态参数(自振频率、振型和阻尼比)是开展抗风、抗震分析以及车桥耦合振动分析的基础。由于铁路悬索桥数量明显少于公路悬索桥，对其模态参数特征的相关研究，特别是现场实测的研究很少。日本对已建大跨度铁路悬索桥如大鸣门桥、南备赞濑户大桥进行了现场模态参数测试，为该试验专门研制了起振器，通过强迫振动以激发结构较大振幅，根据振幅峰值及振动衰减曲线求出桥梁的自振频率和阻尼比[1-2]。香港理工大学、清华大学先后针对香港青马大桥在钢梁合龙、桥面铺装完成两个阶段进行了现场振动测试，分别识别出桥梁19阶、67阶自振频率和振型；在大桥运营阶段，根据大桥安装的健康监测系统(WASHMS)，中国香港特别行政区政府路政署WONG Kaiyuen识别出青马大桥在0～3.8 Hz内的145阶模态频率[3-4]。与自振频率和振型不同，桥梁阻尼只能通过现场实测的手段得到，由于其影响因素众多，机理复杂，准确测定非常困难[5]。李鹏飞等分析了国内114座公路桥梁(含钢桥20座、钢筋混凝土桥87座、钢混组合梁桥7座)的阻尼比实测数据，结果较为离散，其中3座悬索桥的阻尼比均小于1.5%[6]。何玉珊、张劲泉等采用半功率带宽法实测了单跨888 m钢箱梁悬索桥-虎门大桥的结构阻尼比，加劲梁1阶对称侧弯基频对应阻尼比在1.66%～4.43%变化，平均值为2.48%；加劲梁1阶反对称竖弯基频对应阻尼比在0.79%～2.48%变化，平均值为1.32%；加劲梁1阶反对称扭转基频对应阻尼比在0.24%～0.58%变化，平均值为0.36%，实测结果表明高阶模态的结构阻尼要小很多[7]。华旭刚等开展了基于连续跳车激振的大跨度桥梁阻尼识别研究，结果表明：车辆频率、环境噪声均对模态阻尼比识别结果存在影响；设置合适的障碍物距离和行车速度，可以激振起桥梁的大幅振动[8]。

以连镇铁路五峰山长江大桥等国内外铁路悬索桥为工程背景，采用对比分析、数值模拟、现场实测等手段，对铁路悬索桥的自振频率和振型分布特征，以及模态阻尼比特性等进行了研究。

1 工程概况

五峰山长江大桥采用5跨连续、单跨悬吊的钢桁梁结构，承载4线铁路(设计速度250 km/h)、8车道高速公路，主缆跨度布置为(350+1 092+350) m，加劲梁跨径布置为(84+84+1092+84+84) m，设计成桥状态下，主缆跨中理论垂度为109.2 m，垂跨比为1/10，如图1所示[9-10]。

图1 五峰山长江大桥主桥立面布置(单位：m)

桥梁采用半漂浮体系。塔、梁间在扬州侧/镇江侧各设4组纵向黏滞阻尼器，阻尼器的基本设计参数为：最大阻尼力F=3 000 kN，阻尼行程S=±700 mm，非线性指数α=0.2，阻尼系数C=4 000 kN·(s/m)α。

边墩、辅助墩墩顶及主塔处主桁下部支座均为多向活动支座，竖向承载力分别为25 000，65 000 kN和82 000 kN；塔、墩处加劲梁横向外侧均设横向抗风支座，抗风支座预压力1 600 kN，抗压刚度310 kN/mm，边墩与辅助墩处抗风支座弹性压缩量5 mm，主塔处抗风支座弹性压缩量10 mm；主桥端横梁中部下方设置多向活动球型支座，竖向承载力5 000 kN[11]。

2 铁路悬索桥模态参数测试与识别

2.1 桥梁自振频率与振型分析

在进行现场模态参数测试前，首先建立桥梁整体有限元模型，通过动力特性分析提取桥梁各阶自振频率和振型，作为现场布置测点的依据，同时通过与实测结果对比，验证计算模型的合理性。采用Midas Civil建立全桥空间有限元模型，其中索塔和加劲梁采用梁单元模拟，共26 788个；主缆和吊索采用索单元模拟，共414个。桥墩处双向活动支座采用一般支承模拟，横向抗风支座采用折线本构模型模拟；吊索与加劲梁之间的连接、塔顶主缆与主塔间的连接均采用刚性连接。将结构二期恒载转化为质量，塔梁间阻尼器按弹性连接模拟，连接刚度按等效刚度考虑。计算时考虑缆索垂度、大位移等几何非线性[11]。

给出大桥前10阶的自振频率和振型计算结果，如表1所示[12]。从表1可知，本桥第1阶振型为对称横弯，自振频率0.095 Hz；第2阶振型为正对称竖弯，自振频率0.165 Hz；第3阶振型为反对称竖弯+加劲梁纵漂，自振频率0.178 Hz，以上自振频率与本桥抗风研究中给出的0.093，0.164，0.182 Hz比较吻合[9]。本桥第6阶首次出现加劲梁扭转，与主缆横摆及主塔侧弯耦合(主缆横摆为主)，自振频率0.291 Hz，与本桥风-车-线-桥耦合振动研究中给出的0.301 Hz(桥面板按板单元模拟)、0.298 Hz(将桥面板简化为梁单元)基本一致[9]。本桥第2阶扭转振型出现在第11阶，对应自振频率0.336 Hz，同样与主缆横摆耦合，之后第12阶、13阶振型均为主缆横摆+加劲梁扭转，自振频率分别为0.356，0.359 Hz。其中，第13阶自振频率与本桥抗风研究中给出的0.369 Hz接近[9]。综上所述，本文计算的自振频率和振型与既有研究结果比较吻合，可作为后续振动测点布置和模态实测结果相互验证的依据。

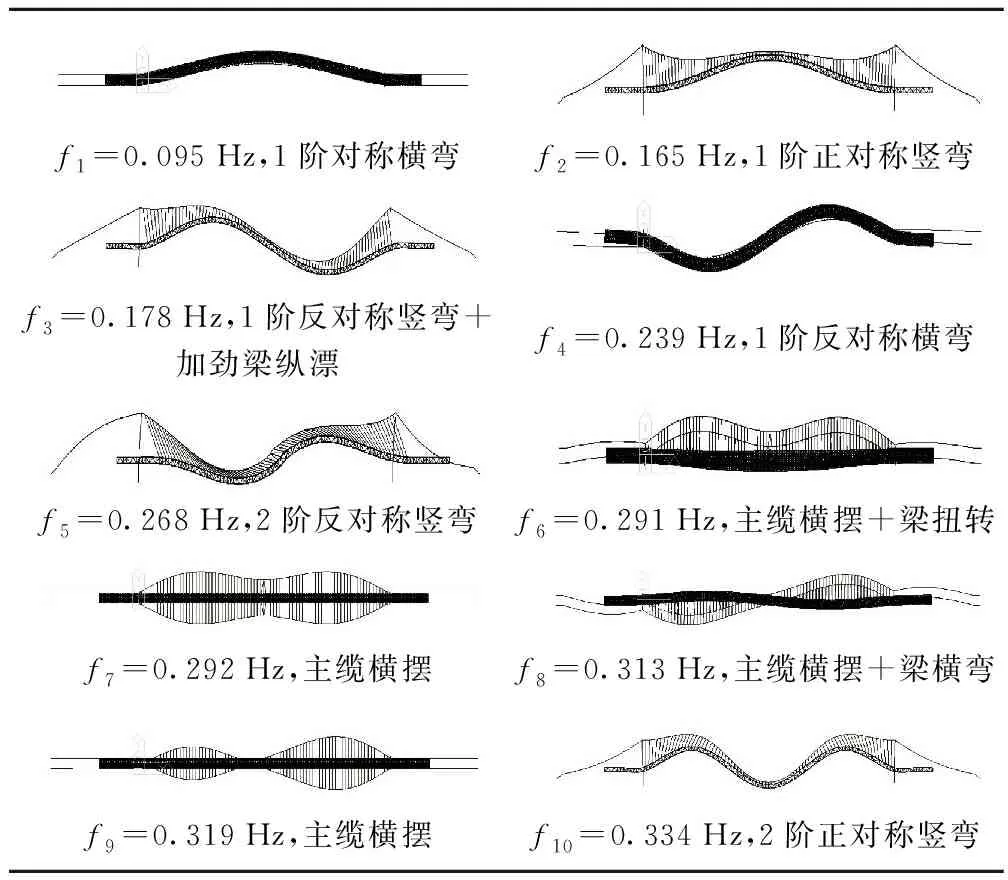
表1 五峰山长江大桥前10阶自振频率与振型计算结果

2.2 桥梁模态参数测试方案

(1)环境激励法测试

五峰山桥模态参数测试属于桥梁动载试验的内容之一，首先采用环境激励法进行桥梁自振频率、振型和阻尼比的测试(脉动法)。根据有限元计算结果和关注的加劲梁竖向、横向和扭转模态，在大桥主跨16等分点、边跨和辅助跨4等分点共布置89个测点，其中横向振动测点31个、竖向振动测点54个，纵向振动测点4个。两桥塔纵、横向各布置2个测点，共4个测点。脉动试验共布置93个测点[12]。

(2)移动加载车定点加载测试(图2)

图2 移动式线路动载加载试验车定点加载测试

考虑到不同激励方式、振幅大小等对阻尼比的影响，除环境激励法，测试时还采用铁科院自主研发的移动式线路动态加载试验车对桥梁按一定频率施加定点激励，根据桥梁振动响应的衰减特性获取桥梁不同加载频率对应阻尼比(强迫振动法)。加载试验车由动力加载车、仪器车组成，其中仪器车SY999319为铁路统型25T车辆，动力加载车SYJZ0001为东风8B基础上改制而成的新型专用车辆，车载检测系统包含了MTS液压加载系统、加载机构及测力轮对、激光测量系统、速度里程系统、探地雷达系统等[12-13]。动力加载车SYJZ0001整备质量126 t，轴重21 t，换长2.2；仪器车SY999319自重51.3 t，载重4 t，换长2.4。移动加载车垂向最大加载力(单轮)250 kN，最大加载频率可达45 Hz；横向最大加载力(单轴)150 kN，最大加载频率可达15 Hz。

移动加载车定点加载测试阻尼比的原理为：在环境激励法测得桥梁自振频率和振型基础上，加载车在对应振型响应最大的位置施加以桥梁自振频率变化的正弦动态荷载，使桥梁能够以此频率对应的振型振动，然后停止动态加载车的激励，使桥梁以此频率对应的振型衰减，通过分析桥梁的振动衰减信号得出桥梁对应振型的阻尼比。

2.3 环境激励法测试结果

采用环境激励法实测得到大桥前16阶振型，对应自振频率从0.109 Hz变化至1.185 Hz。部分实测自振频率与计算值的对比如图3所示。从图3可见，实测值与计算值基本在45°等值线附近，实测自振频率与计算值比较接近，实测值略大于计算值。进一步给出各阶频率对应的阻尼比实测值，如表2所示。从表2可见，不同振型对应阻尼比存在较大差别，加劲梁1阶对称横弯振型的阻尼比为0.75%～1.04%，平均值为0.90%；加劲梁1阶对称竖弯振型的阻尼比为0.50%～0.65%，平均值为0.58%；加劲梁1阶扭转振型的阻尼比为0.23%～0.45%，平均值为0.34%，表明3个基本振型对应的阻尼比横弯最高，竖弯次之，扭转居末。另外还注意到，高阶振型对应的阻尼比普遍较小，如加劲梁横向2阶(对应第4阶计算自振频率)实测阻尼比为0.25%～0.32%，平均值0.29%；加劲梁竖向3阶(对应第10阶计算自振频率)实测阻尼比为0.28%～0.30%，平均值0.29%，明显小于加劲梁竖弯基频对应阻尼比。

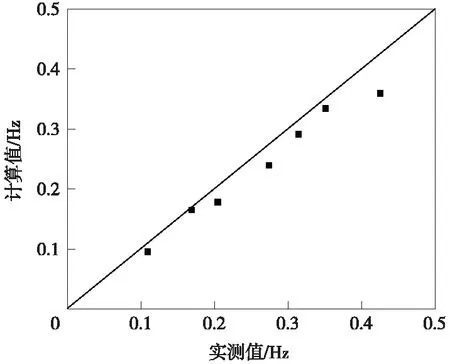
图3 环境激励法实测自振频率实测值与计算值

2.4 定点加载阻尼比测试结果

根据环境激励法实测的大桥自振频率结果确定移动加载车的定点加载具体方案。根据不同振型对应振动响应的最大位置，动态加载试验车在主跨跨中定点加载0.169，0.314，0.425 Hz的正弦动态激励力，分别激励桥梁的竖向1阶正对称振型、扭转与横弯耦合振型、扭转1阶振型，测试响应最大的主跨跨中位置的振动信号；在主跨L/4处加载0.204，0.705 Hz 的正弦动态激励力，分别激励桥梁竖向2阶反对称振型、扭转2阶反对称振型，测试响应最大的主跨L/4处的振动信号；在辅助跨跨中加载0.169，0.314，0.425 Hz的正弦动态激励力，分别激励桥梁的竖向1阶正对称振型、扭转和横向耦合振型、扭转1阶振型，测试辅助跨响应较大的跨中位置的振动信号。以上3种不同的定点加载工况，加载车竖向加载激励力均为(85±65) kN，最大激励力为150 kN，在下行线单线加载(图2)。因主要关注本桥竖向和扭转振型阻尼比，同时桥梁恒载较重，移动加载车未在横向施加作用力。

在以一定加载频率施加正弦动态激励力过程中，桥梁均以此频率对应的振型振动，表明环境激励法测试自振频率结果的准确性。以大桥主跨跨中施加0.314 Hz的正弦激励力为例，给出其振动激励和衰减波形实测结果，如图4所示。针对本桥，由于辅助跨仅84 m，在辅助跨跨中进行定点加载时，桥梁振动信号较弱，阻尼比计算误差较大，故不再给出此工况对应结果。

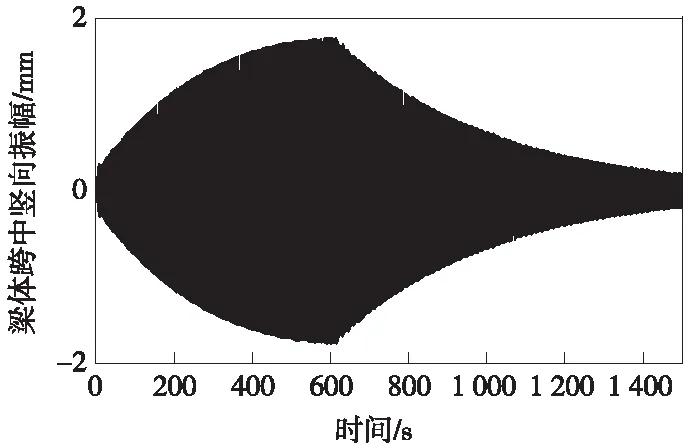
图4 主跨跨中竖向振动时程(加载频率0.314 Hz)

定点加载得到的桥梁振动阻尼比与脉动阻尼比实测值的对比结果如表3所示。从表3可见，1阶正对称竖弯振型(0.169 Hz)对应的定点加载测试阻尼比为0.85%～0.99%，平均值为0.92%，较脉动阻尼比0.58%大；但1阶反对称竖弯振型(0.204 Hz)对应的定点加载测试阻尼比又比脉动法实测阻尼比小。其余加载频率均对应扭转振型，定点加载阻尼比总体比脉动阻尼比更大些，其中主缆横摆+加劲梁扭转振型(0.314 Hz)对应的定点加载测试阻尼比为0.25%～0.69%，平均值为0.47%，大于脉动阻尼比平均值0.34%；加劲梁1阶扭转振型(0.425 Hz)对应的定点加载测试阻尼比为0.22%，与脉动阻尼比平均值0.27%接近；加劲梁2阶扭转振型(0.705 Hz)对应的定点加载测试阻尼比为0.24%～0.28%，平均值为0.26%，大于脉动阻尼比平均值0.19%。

表3 定点加载桥梁阻尼比实测值与脉动阻尼比汇总

3 国外铁路悬索桥模态参数测试分析

3.1 美国代表性铁路悬索桥动力特性测试

美国在19世纪末、20世纪初建造了几座代表性的铁路(轨道交通)悬索桥，典型的如1883年建成的纽约布鲁克林桥、1909年建成的曼哈顿桥。以布鲁克林桥为例，对其动力特性测试和结果进行分析[14]。布鲁克林桥为主跨487 m的悬索桥，因增加了部分斜拉索提高了结构冗余度，保证了该桥在吊杆和拉索发生严重腐蚀而需更换时不必中断交通。大桥早期承载2线有轨电车、4车道机动车和人行道，之后调整为4线铁路轨道，后又全部改为机动车道和人行道，纽约市交通运输部在2003年8月对该桥进行了动力性能现场测试，此时距离大桥运营已121年。采用ANSYS 7.0建立该桥3D有限元模型，通过模态分析得到该桥的1阶横弯、竖弯和扭转振型，对应自振频率分别为0.180，0.318，0.401 Hz[14]。大桥动力特性现场测试由里海大学大型复杂结构国家工程研究中心(ATLSS)负责，分别开展了环境振动监测和强迫振动试验，其中环境振动测试提取了35阶模态振型，自振频率从0.0～2.5 Hz，有34阶在有限元模型中被识别，实测值与计算值比较吻合，最大误差在8%左右。进一步针对人致振动敏感的频率范围进行了强迫振动试验，其中竖向激振频率为1.5～2.5 Hz，横向激振频率为0.5～1.5 Hz。采用美国陆军工程兵团研究与发展中心(ERDC)提供的电液式激振器，质量为6.5 t，可施加25 kN激振力，激振器在主跨跨中、L/4以及边跨跨中进行激振试验，采集横向和竖向振动响应。通过扫频试验获取每一个共振频率，之后进行共振试验。待得到结构稳态响应后，快速停止激振使桥梁自由振动，采用自由振动衰减法计算阻尼比，以主跨3阶横弯为例(在主跨L/4处激振，自振频率0.58 Hz)，实测阻尼比为0.85%，如图5所示。采用此方法对18阶振型进行了实测，实测阻尼比变化范围0.7%～3%[14]。

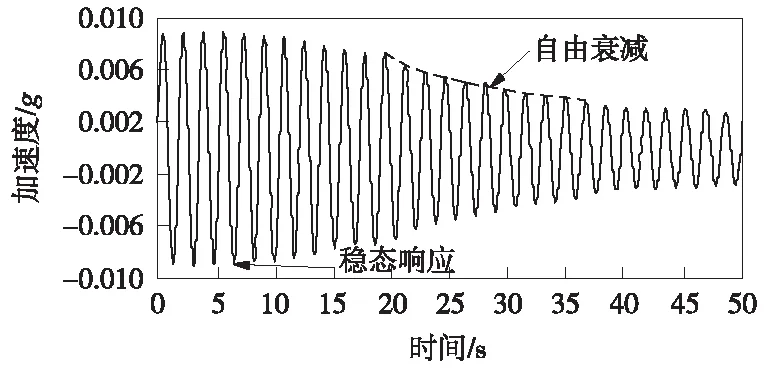
图5 布鲁克林桥主跨3阶横弯共振响应[14](f=0.58 Hz)

3.2 日本代表性铁路悬索桥的动力特性测试

日本针对南备赞濑户大桥、大鸣门桥等大跨度悬索桥开展了详细的动力性能现场实测。南备赞濑户大桥主桥跨径布置为(274+1 100+274) m，采用双塔三跨连续加劲钢桁梁结构型式，承载双线铁路、4车道公路，铁路桥面主桁宽30 m，桁高13 m，加劲梁自重314 kN/m；大鸣门桥主桥跨径布置为(93+330+876+330) m，采用双塔三跨两铰加劲钢桁梁结构型式，承载双线铁路、6车道公路，铁路桥面主桁宽34 m，桁高12.5 m，加劲梁自重235 kN/m。两座铁路悬索桥设计速度均为160 km/h[2]。

根据本州—四国桥梁风洞试验指南的规定，用于评估结构阻尼的参考振幅标准，在弯曲振动中应不小于梁宽的1/200，则对应南备赞濑户大桥振幅应不小于150 mm，对应大鸣门桥振幅应不小于170 mm；在扭转振动中不小于0.5°。为此，采用特别研制的起振器，两个起振器分别布置于公路桥面的左右两侧，单个总重约840 kN，激振频率0.1～2.0 Hz，最大激振力200 kN(0.5 Hz)。实测结果表明，在较低振幅条件下，多数振型阻尼比随振幅增大而增大，当振幅增加到一定量值后，阻尼比基本保持不变。两座大桥模态参数的计算和现场实测结果如表4、表5所示[2]。

表4 南备赞濑户大桥模态参数结果

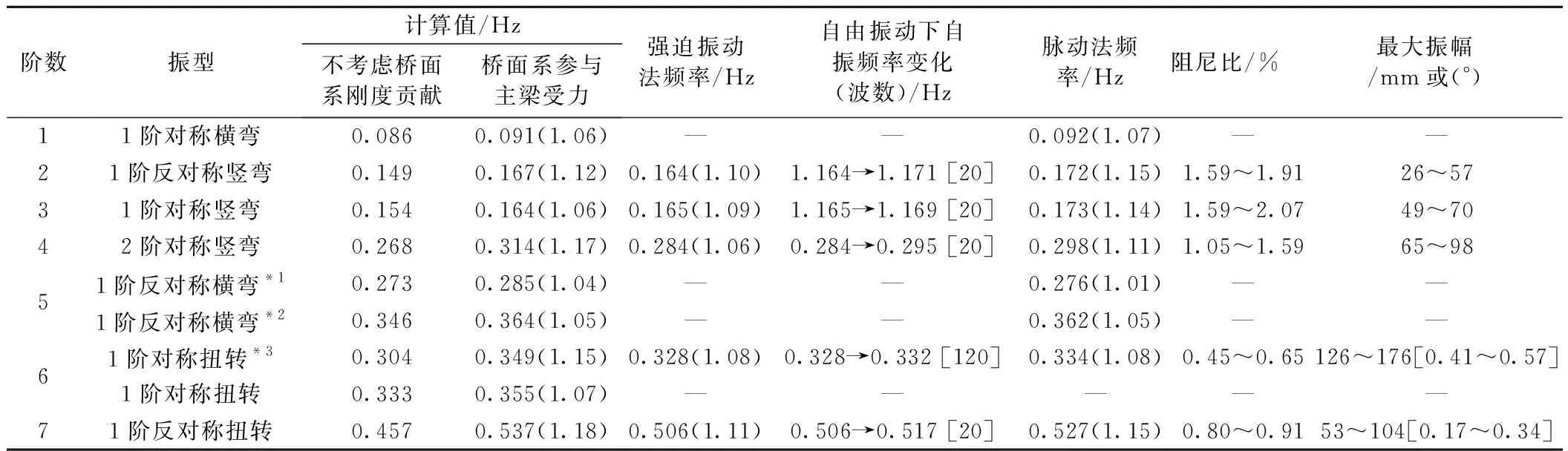
表5 大鸣门桥模态参数结果

从表4、表5可见，竖弯振型对应阻尼比明显大于扭转振型阻尼比，南备赞濑户大桥竖弯振型对应阻尼比变化0.64%～1.75%，均值1.2%，1阶到4阶竖弯振型阻尼比差别不大；大鸣门桥竖弯振型阻尼比变化1.05%～2.07%，均值1.56%；南备赞濑户大桥、大鸣门桥的扭转振型阻尼比变化分别是0.48%～0.70%、0.45%～0.91%，均大于五峰山桥的阻尼比。从表中还可见，激振器能够激发的最大振幅普遍小于本州-四国桥梁风洞试验指南中规定的参考振幅标准。从自振频率看，两座桥梁的实测自振频率与计算值均比较吻合，如图6所示，表明有限元模型能够合理反映大桥的动力特性。

图6 日本两座铁路悬索桥的自振频率实测值与计算值

4 铁路悬索桥模态参数分布特征初步统计

根据上述结果，研究铁路悬索桥自振频率和阻尼比的分布特征，并给出初步估算公式。《公路桥梁抗风设计规范》给出了公路双塔悬索桥反对称竖向弯曲基频、对称竖向弯曲基频、反对称和对称扭转基频等的基频估算公式，其中，关于竖弯基频的公式较为简洁，而扭转基频公式比较复杂[15]。但由于铁路悬索桥刚度一般较公路悬索桥大[16-17]，相关公式不能直接用于铁路悬索桥。以主跨跨径500 m以上双塔悬索桥的反对称竖弯振型为例，其基频估算公式如下[15]

(1)

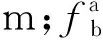
为此，统计了多座公路、铁路悬索桥反对称竖弯基频的实测值[2-4，7，12，18-24]，并与式(1)结果进行对比，结果如图7所示。从图7可见，公路悬索桥实测值与规范值总体符合较好，表现为主跨800～1 000 m内相对误差在10%以内，规范值略小；主跨1 300 m以上规范值略大，相对误差也在10%以内；按式(1)计算的铁路悬索桥1阶反对称竖弯频率均小于现场实测值，其中香港青马大桥相对误差为9.96%，差别最小(实测值0.114 Hz，规范值0.104 Hz)；五峰山长江大桥相对误差最大，为83.77%(实测值0.204 Hz，规范值0.111 Hz)；日本两座铁路钢桁梁悬索桥对应相对误差在30%左右。这主要是由于五峰山桥为高速铁路钢桁梁悬索桥，整体刚度更大些。

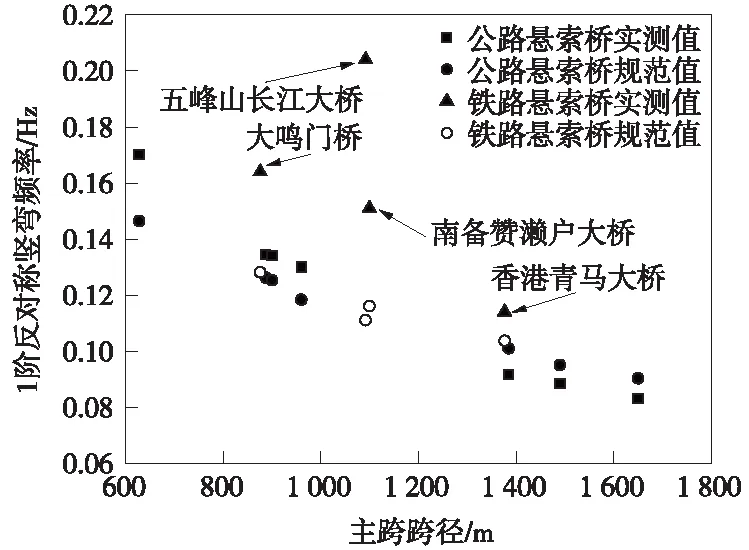
图7 1阶反对称竖弯基频实测值与规范值对比

统计了纽约布鲁克林桥、日本大鸣门桥和南备赞濑户大桥、我国香港青马大桥和五峰山长江大桥等5座铁路悬索桥的基频值[2-4，12]，初步给出关于主跨跨径的基频估算公式及相关系数，结果如图8所示。从图8可见，1阶对称横弯基频、1阶对称竖弯基频与主跨跨径之间的关系均可以表达为幂函数形式，1阶扭转基频与主跨跨径之间的关系可以表达为线性函数形式，相关性均较强。

图8 铁路悬索桥基频经验公式(初步拟合)

进一步统计了五峰山长江大桥、日本两座铁路悬索桥阻尼比实测数据与自振频率之间的关系，如图9所示。从图9可见，对五峰山长江大桥，采用不同激励方式得到的阻尼比随自振频率增大总体上表现为逐渐减小的趋势，对大鸣门桥也具有类似趋势，但南备赞濑户大桥的阻尼比分布比较杂乱。我国公路悬索桥设计规范针对钢桁加劲梁悬索桥的结构阻尼比分别给出下限值0.3%和上限值0.5%，是在结合现场实测结果和日本规范基础上给出的，其中下限值对应高阶振动模态，上限值对应1阶或低阶振动模态[25]。从铁路钢桁梁悬索桥的实测结果来看，0.3%～0.5%的阻尼比是在考虑高阶模态阻尼较低基础上对结构阻尼偏于保守的一个估计，这对于评价悬索桥高阶模态涡激振动及其他结构动力响应是必要的。

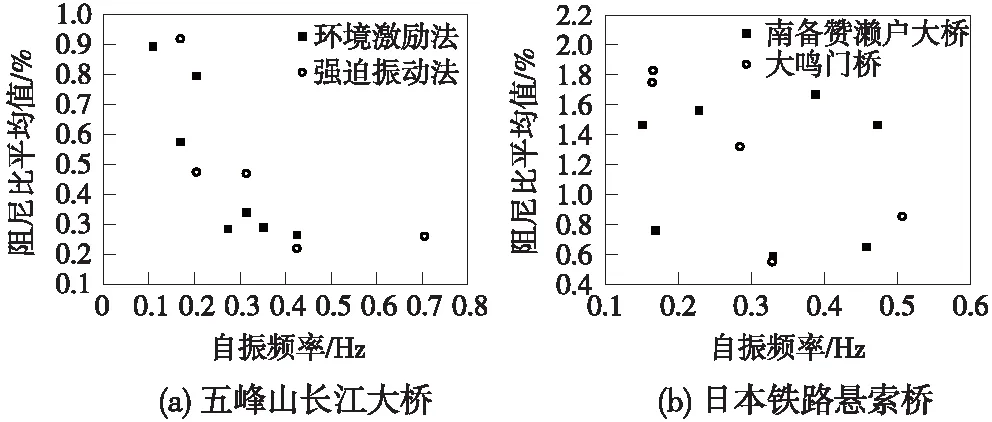
图9 铁路悬索桥实测阻尼比与自振频率关系

5 结论

以连镇铁路五峰山长江大桥为工程背景，从理论分析、现场实测两方面，对其自振频率和振型特征进行了研究，分别采用环境激励法、强迫振动法(定点加载)测试了大桥阻尼比，并与国外铁路悬索桥的模态结果进行了对比，主要研究结论如下。

(1)采用环境激励法、强迫振动法得到的铁路悬索桥自振频率和振型，与理论计算值吻合较好，五峰山长江大桥实测自振频率略大于理论计算值。美国布鲁克林桥，日本南备赞濑户大桥、大鸣门桥等几座代表性铁路悬索桥对应自振频率实测值与理论计算值也比较吻合。

(2)对铁路悬索桥，1阶对称横弯、竖弯基频的估算公式可采用关于主跨跨径的幂函数形式；1阶扭转基频与主跨跨径线性相关；1阶反对称竖弯基频大于公路悬索桥经验公式计算值，且不同的铁路悬索桥差别较大(公轨两用、公铁两用、高速铁路+公路)，相对偏差9.96%～83.77%。

(3)铁路悬索桥阻尼比与激励方式、振型阶数、振型类型、振幅大小等众多因素相关，准确确定的难度很大。从五峰山长江大桥阻尼比实测结果来看，强迫振动法获取的结构阻尼比整体上要大于环境激励法结果，但强迫振动法振幅较小，也会对阻尼比测试精度带来一定影响。根据环境激励法，横弯基频对应为0.9%，竖弯基频对应为0.58%，扭转基频为0.34%；强迫振动法对应的竖弯基频阻尼比为0.92%，扭转基频阻尼比为0.47%。同时，五峰山长江大桥阻尼比随自振频率增大趋于降低。与五峰山桥比较，日本两座铁路悬索桥阻尼比的实测结果整体更大一些。

(4)本文首次在国内通过采用移动加载设备定点加载的方式完成了悬索桥基于强迫振动法的阻尼比测试，得出较脉动法更大的阻尼比实测结果。从现场试验情况来看，由于本桥质量和刚度均较大，加载车激发出的振幅并不大。针对不同的大跨度铁路桥梁，研发易于移动、质量相对较轻的激振器设备，并建立大跨度铁路桥梁模态参数特别是阻尼比的测试标准，是下一步努力方向。