基于制动工况的地铁车轮热负荷研究

李洪晓, 孙培文, 郝润之, 贾一君, 朱爱华

(1.北京建筑大学 机电与车辆工程学院， 北京 100044；2.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室， 北京 100044；3.汉唐技术有限公司， 浙江 杭州 310003)

随着现代化城市的快速发展，地铁成为人们必不可少的出行工具。为人们提供方便的同时，地铁车辆短时间内进行频繁制动所产生的热负荷对车轮造成了严重的损伤，作为地铁车辆走行部的关键构件，保证车轮的运行性能尤为重要。

针对车轮制动热负荷，研究人员从理论、仿真、试验等方面进行了大量的研究。郭奇宗[1]通过分析某型高速动车组紧急制动工况的试验数据，针对该型动车组制动盘比热容和导热系数的曲线特性进行了对比，搭建了符合该型动车组的制动盘热负荷仿真计算平台。TUDOR等[2]分析了轮和闸瓦以及轮轨之间的热量分配系数，并据此建立了用于评估车轮和制动闸瓦温度场的模型。关莹等[3]对120 km/h、140 m/h和160 km/h速度标尺下的温度场与应力场数据进行了分析。王京波[4]分析了货运列车的闸瓦类型对车轮的热影响，确定了合成闸瓦的适用范围。TEIMOURIMANESH等[5]研究了铁路踏面制动过程中的摩擦热以及轮轨接触时的热量传递过程，确定了轮轨接触条件下钢轨的冷却效应，发现钢轨的冷却效应对踏面的局部温度影响较大。张宗威[6]通过ANSYS有限元软件建立货车新轮三维有限元模型,针对坡道长度10～20 km连续延展的不同坡长工况,进行货运列车匀速下坡制动热负荷分析。王治颖[7]在ABAQUS软件中建立跨座式单轨车辆制动盘和摩擦片有限元仿真模型，研究温度场分布情况以及变化规律。赵凯凯[8]以某地铁车辆为研究对象，基于传热学和断裂力学理论，利用热力耦合有限元方法分析并计算了闸瓦制动下车轮的温度场和应力场分布情况以及制动热对踏面表面热裂纹的影响，发现车轮踏面与闸瓦的接触面积对踏面热裂纹扩展的影响非常显著。张萍[9]利用ANSYS建立车轮踏面制动热负荷模型，对比分析了制动形式、制动加速度、闸瓦材料、辐板结构等条件对车轮热负荷的影响。VERNERSSON[10]将踏面制动的二维有限元热模型应用于车轮和制动块之间温度的常规计算，实现了对整个火车路线温度的模拟。李言义等[11]对新型100 km/h地铁列车踏面制动的可靠性进行了有限元分析，发现踏面制动不能满足其对踏面损伤的要求，需采用盘式制动。尹志凯等[12]使用MSC.MARC软件，采用直接热- 机耦合的方式来分析不同工况下的踏面温度和应力。赵长龙[13]建立了上海地铁A型地铁车轮有限元模型，在偏向实际的曲线、直线、道岔3种工况下，分析其制动时的热应力。杨智勇等[14]通过分析北京地铁10号线列车紧急制动和全程往返制动2种极端情况，评估地铁列车车轮的服役安全性。张琪等[15]通过对比研究不同闸瓦宽度、辐板形式、轮辋厚度对热负荷的影响，提出基于较小制动热负荷的车轮几何参数建议。路象群[16]对广州地铁A5型车在电空制动情况下电制动退出时的速度值进行了实际测量，得出电制动的退出速度值在4.0 km/h左右。龚熙恒[17]通过电制动制动至零(Electric Brake to 0，EB0)模式对电空转换的过程进行控制，证明了电空制动控制技术能满足列车自动驾驶系统对准确停车的控制要求,并降低了闸瓦和车轮间的磨损。李云峰等[18]通过对地铁车辆进行数据实测，验证了电空配合关系。张建国[19]对新旧轮在不同制动工况下的制动热负荷进行评估，证明新旧车轮的制动性能均符合标准。

以上研究确实解决了车轮热负荷的多数问题，但忽略了不同制动材料在不同初速度以及不同制动减速度下的热负荷响应。因此，本文以高磨合成闸瓦和中磷铸铁闸瓦作为研究对象，研究2种闸瓦材料在不同制动初速度和不同制动减速度的条件下对车轮热负荷的影响。

1 模型搭建

1.1 车轮有限元模型

模型的建立分为2步，首先使用CAD软件建立车轮剖面模型，再把CAD二维图导入到ANSYS软件中，输入参数建立模型。ANSYS有限元分析是把1个整体拆分成若干个网格来进行网格内的分析，网格划分的越细，结果就会越精确，但是计算量也会越大。本次模拟试验采用自由网格划分方式，划分为376个节点，308个网格。自由网格划分用于空间自由曲面和复杂实体，采用三角形、四边形、四面体进行划分。

图1为地铁车轮有限元模型，车轮选用Φ 840 mm的标准地铁车轮新轮，辐板选用S型辐板，车轮踏面类型为LM型。由于地铁车轮具有对称性，考虑到轮对的结构，建模时只建立单个车轮模型。常温下CL 60钢[20]的参数见表1。

表1 地铁车轮材料的热物理参数

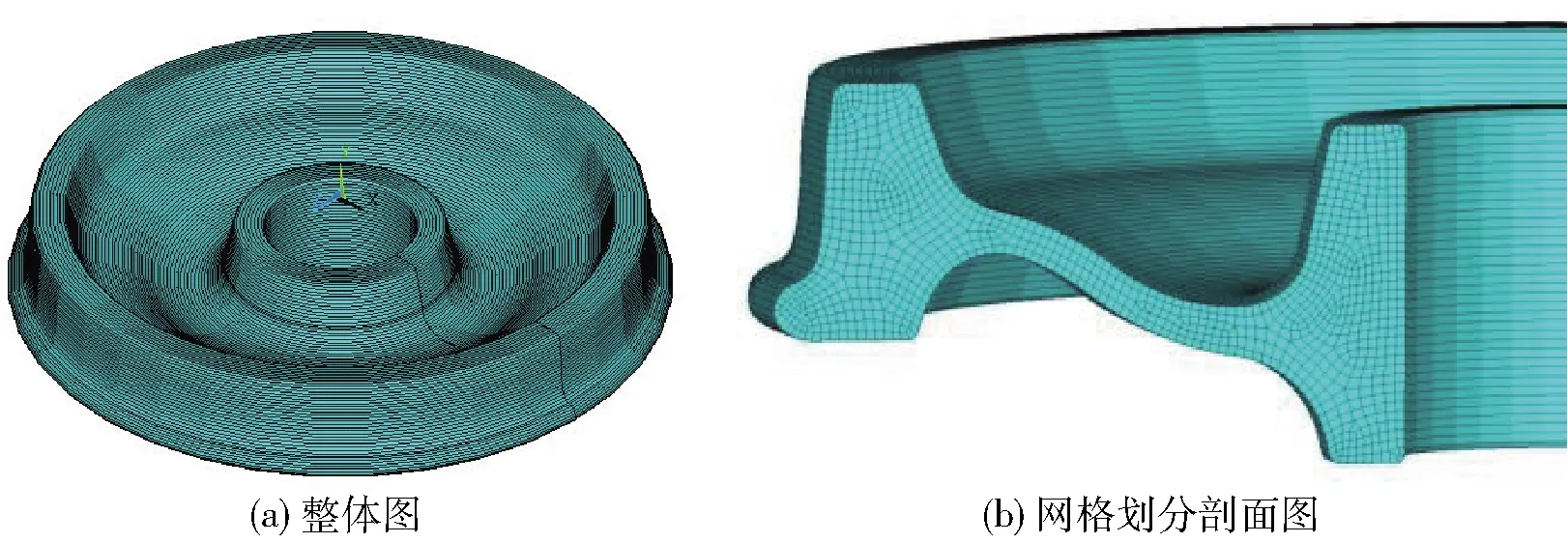
图1 车轮模型Fig.1 Wheel model

1.2 热分析边界条件

在地铁车辆制动阶段，主要有2种热分析边界条件。一种是热的输入，即在闸瓦与车轮直接接触时所产生的热；另一种是热的输出，即车轮和闸瓦上的热量主要通过对流进入空气中。决定以上2种热分析的重要参数为热流密度和对流换热系数。同时，均布热源法是一种简化方案，由于地铁列车车轮转速快，闸瓦和车轮之间摩擦产生的热量可以视为在车轮踏面上均匀分布的热量。以闸瓦中线与名义滚动圆处对齐后的相对位置作为加载位置。

由热力学知识可知，单位时间内通过某一面积的热量称为热流量，单位时间内通过单位面积的热流量称为热流密度。在如今的研究中，根据能量守恒定律，主要采用能量转化法计算地铁车辆轮对的热流密度。

在能量转化法中，以理想状态下车辆的动能全部转化为热能来计算踏面的热流密度值。则在车辆制动时闸瓦与轮对的摩擦热量Q(t)为：

(1)

式中：v0为制动阶段的初速度，单位为m/s；m为每个车轮的载荷，即轴重的二分之一，单位为kg；t为制动所需的时间，单位为s；ab为制动阶段的列车加速度，单位为m/s2。

由式(1)求导数可知理论热流密度Pd(t)为[21]：

(2)

但是实际的制动过程，会比理想情况复杂许多，闸瓦会吸收一部分热量，这时就需要考虑闸瓦和车轮间的热量分配比例关系，需要引入新概念热流分配系数η：

(3)

式中：λw、λb、aw、ab分别是车轮导热系数、闸瓦导热系数、车轮导温系数和闸瓦导温系数。

即实际状态下，地铁车轮的实际踏面热流密度q(t)为：

(4)

式中：S为踏面与车轮之间的摩擦带面积， 单位为mm2，大小为3.01×104mm2。

由上述可知，制动初速度与实际踏面热流密度成正比，摩擦带面积与实际踏面热流密度成反比。

对流换热是指，流体流过固体表面时，2个物体表面之间热量的传递。对流换热量φ为[22]：

φ=hAΔt

(5)

式中：Δt为两者之间的温度差值，单位为℃；A为对流换热接触面的面积，单位为mm2；h为对流换热系数。

在制动过程中，空气的转动速度对空气流过车轮表面进行热传递起着决定性作用，因此在不同的车速条件下，对流换热系数h的数值模型有所差异。在传统的研究中，确定对流换热系数的方法主要有理论法和试验法。理论法是在建立的对流换热方程组的基础上，通过数学运算求得对流换热系数的数值或表达式。而试验法是在试验台进行测试并整理数据，求得各特征数之间的函数关系。因为影响地铁车轮对流换热系数的主要因素是车辆运行速度。所以本文在计算对流换热系数h时采用试验法所得到的经验公式[23]：

h=0.382 8+14.39v(t)

(6)

式中：v(t)为地铁列车的运行速度，单位为m/s。

2 不同工况下地铁车轮制动热负荷分析

由表2可知，地铁车轮使用的中磷铸铁闸瓦与高磨合成闸瓦热扩散系数和对流换热系数相差较大，闸瓦类型可能会对车轮热负荷造成较大影响。同时由式(3)和式(4)可知，列车制动时的初速度与减速度也对热流密度有影响。因此，这3组数据可以作为模拟试验中的变量进行分析。

表2 地铁车轮闸瓦材料的热物理参数

在实际运营中，地铁列车的制动减速度主要为常用制动减速度和紧急制动减速度，分别为0.8 m/s2和1.0 m/s2，因此选择以上2种制动减速度研究对车轮温度的影响。同时我国三动三拖或四动两拖六编组地铁列车的最高速度为80 km/h，即约22 m/s，而在有小半径曲线等限速条件下，列车速度会被限制为55～60 km/h，即约16 m/s，因此选择以上2种制动初速度研究其对车轮温度的影响。

由上述分析可得出，应选择不同闸瓦类型、不同制动减速度、不同制动初速度3组变量共8组数据做对照试验。模拟试验中取列车轴重为14 t，闸瓦横向宽度为86 mm，给定车轮与闸瓦的初始温度为40 ℃，具体模拟试验见表3。

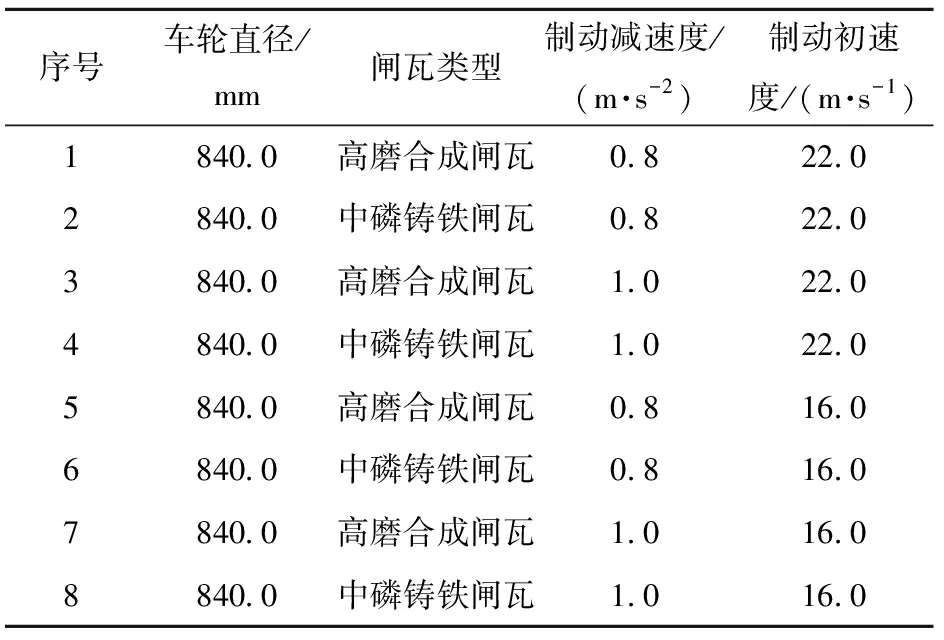
表3 模拟试验组

2.1 温度场计算结果

表4为8种工况下的运算结果，数据选取了制动时间、最终点温度、最高点时间和最高温度。

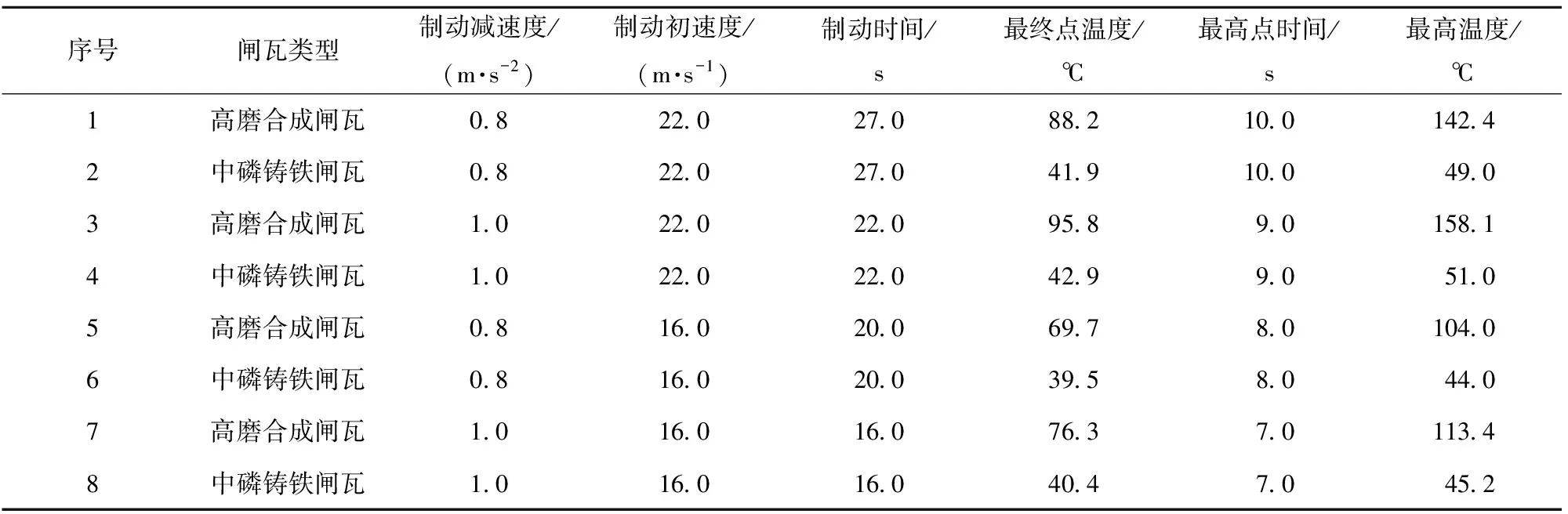
表4 Ansys模拟试验结果

以工况1和工况6为例，图2为2种工况对应的输出结果云图，图中红色位置即为车轮踏面的最终点温度，工况1对应的最终点温度为88.2 ℃，工况6对应的最终点温度为39.5 ℃。

图2中明显可以看出闸瓦与车轮踏面的接触位置温度最高，特别是名义滚动圆附近的红色区域是整个车轮在基础制动过程中温度最高的部分，制动热量在此产生并以此为中心向外辐射。

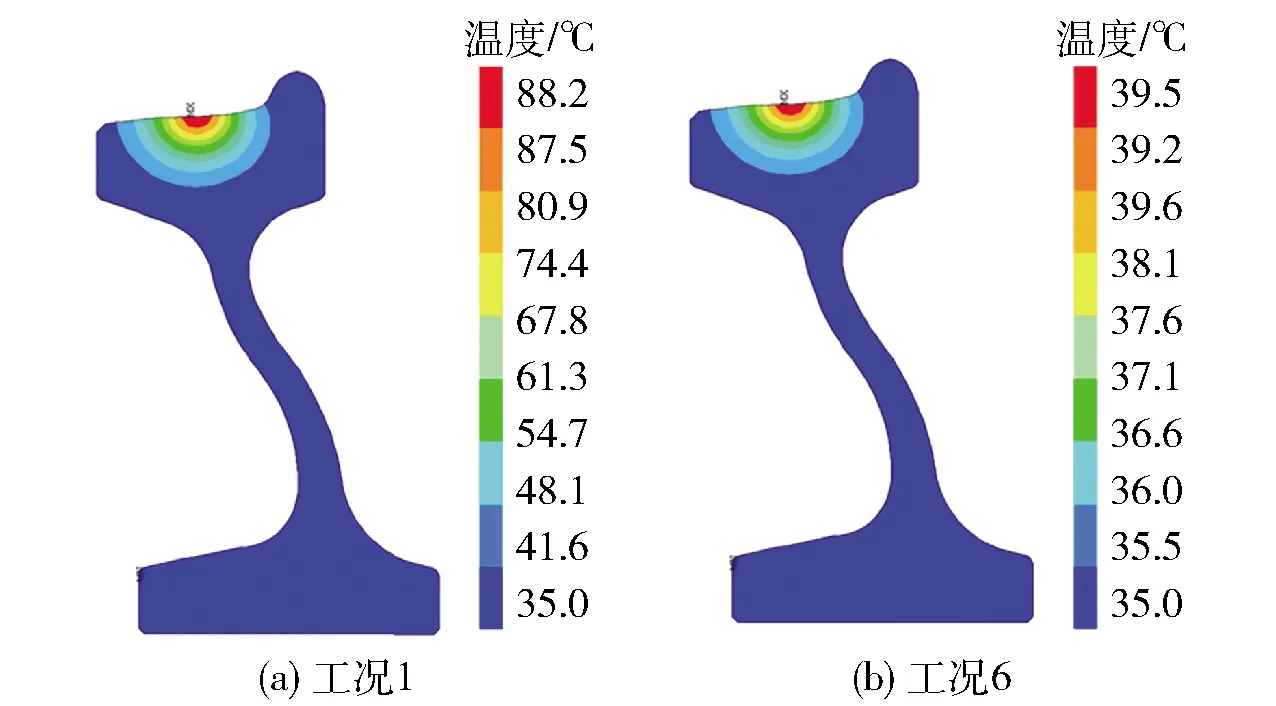
图2 车轮最终点温度分布云图Fig.2 The temperature distribution cloud map at the final point of the wheel

2.2 不同闸瓦类型对车轮温度曲线的影响

研究不同闸瓦类型对车轮温度曲线的影响，需要固定制动减速度和制动初速度2组数据，将闸瓦类型作为唯一变量。为了保证结果分析的准确性，不止研究其中一对数据，而是将4组数据全部对比。这样可以尽可能消除偶然误差，使结果更加准确。

图3为不同闸瓦类型对应的车轮热负荷变化。由图3可知，4组数据的变化趋势基本相同，均是高摩合成闸瓦对应的车轮温度远远高于中磷铸铁闸瓦，且随着制动初速度以及制动减速度的变化，相对中磷铸铁闸瓦，高磨合成闸瓦对应的车轮温度变化较大。究其原因，在表2中可知，中磷铸铁闸瓦的热流分配系数为49.3%，高磨合成闸瓦的热流分配系数为93.4%。在闸瓦与车轮摩擦制动的过程中，高磨合成闸瓦会将绝大部分产生的热量传递给车轮，而中磷铸铁闸瓦约传递一半，这就使得高磨合成闸瓦的车轮温度远高于中磷铸铁闸瓦。但是车轮温度高并不代表性能差，高磨合成闸瓦的热扩散系数和热流分配系数远大于中磷铸铁闸瓦，散热更快，且最高温度控制在170 ℃以下，低于车轮材料的许用温度400 ℃。由此可看出高磨合成闸瓦更适用于地铁列车制动工况。

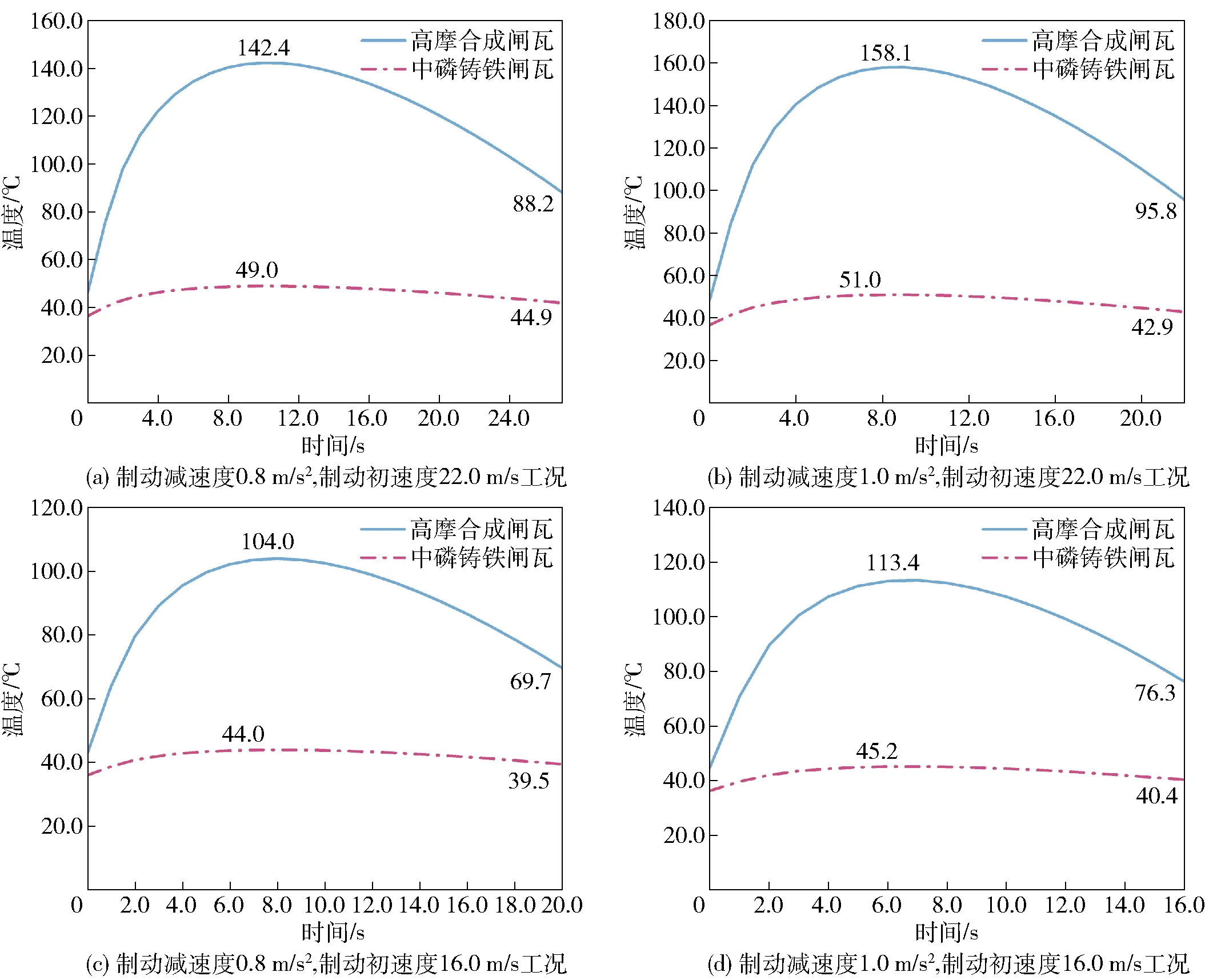
图3 不同闸瓦类型对应的车轮热负荷变化Fig.3 Wheel thermal load changes corresponding to different brake shoe types

2.3 不同制动减速度对温度曲线的影响

图4为不同制动减速度对应的车轮热负荷变化。由图4可知，在相同初速度时，制动减速度为1.0 m/s2时对应的车轮最高温度均高于0.8 m/s2组。同时制动减速度为1.0 m/s2与0.8 m/s2时对应的温度变化均是先增加后减少，其中高磨合成闸瓦对制动减速度的变化反应比较明显。如图4(a)所示，初速度为22.0 m/s时，2种制动减速度对应的车轮最高温度相差达15.7 ℃；中磷铸铁闸瓦对应的车轮温度差异较小，2种减速度对应的车轮最高温度差仅为2.0 ℃。由此可以看出，在运用高磨合成闸瓦的地铁列车上，相对于制动减速度为1.0 m/s2，制动减速度为0.8 m/s2时能显著降低车轮温度。

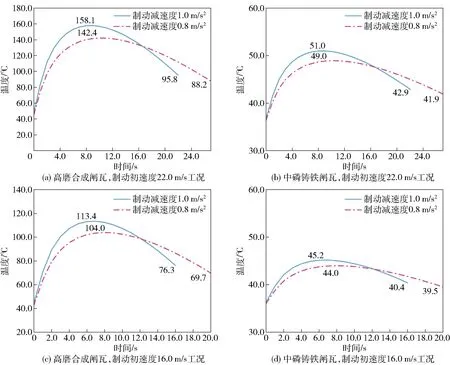
图4 不同制动减速度对应的车轮热负荷变化Fig.4 Wheel thermal load changes corresponding to different braking deceleration

2.4 不同制动初速度对温度曲线的影响

图5为不同制动初速度对应的车轮热负荷变化。由图5可知，制动初速度为22.0 m/s与16.0 m/s时对应的温度变化均是先增加后减少。相对于制动初速度为16.0 m/s，制动初速度为22.0 m/s时的车轮温度更高，制动时车轮温度大约在9.0 s左右达到温度最高点。且高磨合成闸瓦相比于中磷铸铁闸瓦的温度变化更大，制动减速度为1.0 m/s2时，如图5(c)所示，2种制动初速度对应的最高温度差异达到44.7 ℃。

图5 不同制动初速度对应的车轮热负荷变化Fig.5 Wheel thermal load changes corresponding to different initial braking speeds

3 不同制动减速度下的对照试验结果分析

通过研究不同工况下的地铁车轮热负荷情况，得到了可以有效降低地铁车轮制动热效应的3种方法，分别为使用高磨合成闸瓦、降低制动初速度、降低制动减速度。

地铁实际运行时采用的是电空制动，即车速较高时使用电制动，当车速降低导致电制动效能衰退时切换为空气制动。而通过延长电制动作用时间，从而降低空气制动开始时初速度的方法，将会导致地铁制动的可靠性降低，危及行车安全，所以降低制动初速度这项举措是不可取的。与之相比，虽然减小地铁基础制动时的减速度会相对延长地铁制动的时间，但是对于实际运营的地铁线路来说则更具有实际应用价值。因此，在下文中设置了使用不同制动减速度的对照试验进行研究。

2组模拟试验均采用高磨合成闸瓦，制动初速度为4 m/s的初始工况，对照组选取制动减速度为0.8 m/s2，模拟试验组选取制动减速度0.4 m/s2。表5为对照组与模拟试验组在不同制动减速度下的运算结果，数据选取了制动时间、最终点温度、最高点时间和最高温度。图6为对照组与模拟试验组在不同制动减速度下完成基础制动过程时的车轮最终点温度分布云图，其制动时最高点温度分布情况如图7所示。

表5 ANSYS模拟试验结果

图6 车轮最终点温度分布云图Fig.6 The final point temperature distribution cloud map of the wheel

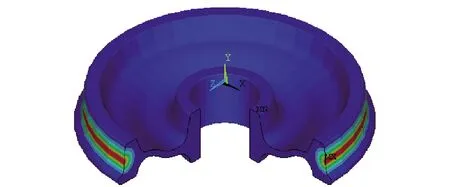
图7 车轮温度最高点分布云图Fig.7 Distribution cloud map of the highest point of wheel temperature

图6、图7中均显示出高摩合成闸瓦与车轮踏面的接触位置温度最高，特别是名义滚动圆附近的红色区域是整个车轮在基础制动过程中温度最高的部分，制动热量在此产生并以此为中心向外辐射。将模拟试验组和对照组的模拟数据进行提取后，2组车轮温度随时间变化的折线如图8所示。

图8 2组车轮的温度对比Fig.8 Temperature comparison of two sets of wheels

地铁制动距离s(t)为：

(7)

式(7)中：s(t)为地铁制动距离，单位为m；v0为地铁列车的制动初速度，单位为m/s；ab为地铁列车的制动减速度，单位为m/s2。

通过以上的对比试验，可以得到在使用高摩合成闸瓦，制动初速度为4 m/s的工况下，将基础制动阶段减速度由0.8 m/s2降低到0.4 m/s2，会使制动阶段最高温度降低2.1 ℃，而制动时间相应延长5 s，根据式(7)计算得到其制动距离会相应延长约5 m，极限温度始终低于车轮许用温度400 ℃。

4 结论

通过建立地铁车轮热负荷模型，研究不同闸瓦类型、不同制动初速度以及不同制动减速度对车轮动态热负荷的影响规律。仿真分析结论如下：

1)高磨合成闸瓦和中磷铸铁闸瓦均能满足地铁基础制动时的热负荷要求。虽然中磷铸铁闸瓦在地铁基础制动期间的车轮温度更低，但由于车轮本身体积远大于闸瓦体积，这使得热量将集中于闸瓦本身。且中磷铸铁闸瓦本身散热效果较差，使得热量更多地传回车轮，反而不利于控制车轮基础制动时的温升。因此，高摩合成闸瓦更适合地铁的制动工况。

2)地铁实际运行时采用的是电空制动，即车速较高时使用电制动，车速降低时切换为空气制动。因此，通过延长电制动作用时间来降低空气制动开始时的初速度，将会导致地铁电制动作用后期制动的不足，这会对制动可靠性以及行车安全造成不利影响。

3)虽然降低制动减速度会略微延长制动时间，但对于1条单程约20站的常规地铁线路，利用以上模拟结果计算后可得其全程增加的时间不超过2分钟，这对于地铁的运营调度影响较小。

综上所述，在不影响实际线路运行的情况下，选择降低地铁基础制动时的减速度，将有效降低车轮所承受的热负荷，对于延长车轮寿命，保障地铁车辆运行安全性具有一定的指导意义。