离散奇异随机Markov跳变系统的N人Nash博弈
2021-10-13周海英
周海英
(广州航海学院港口与航运管理学院,广州 510725)
1 引言与研究背景
现实实际中的许多系统在结构和参数等方面往往都表现出随机变化的规律,当这种规律服从Markov过程时,这样的系统被称为Markov跳变系统[1]。Krasovskii和Lidskii在1961年首次提出了Makov跳变系统的概念,随后,Sworder基于随机最大值原理讨论了带Makov跳变参数的混合线性系统并成功将其应用到实际控制问题。此后,Markov跳变系统因其在制造系统、飞行控制器系统、机器人操作系统、通信系统、神经网络中的分析仿真等方面都有着非常实际的应用背景,引起了国内外学者们的广泛关注。近些年,Markov跳变系统逐渐成为研究热点,相应的研究成果日益丰富[2-6]。一般地,仅由微分方程描述的系统,称为正常系统;由微分代数方程(组)描述的系统,称为奇异系统。奇异系统相较正常系统,更具广泛适用性,其实际应用背景丰富,如电网系统,化工过程,核能源反应堆以及社会经济领域等等。因此,学者们也越来越重视对奇异Markov跳变系统的分析以及研究。Tao等研究了时滞奇异随机Markov跳变系统的容许性问题[7],Chávez-Fuentes等探讨了离散奇异Markov跳变系统的正则和稳定性条件[8],Yu等探讨了时变奇异马尔可夫跳跃系统的观测控制问题[9],Zhang等探讨了奇异Markov跳变系统的控制问题[10]。
另一方面,微分博弈理论由于在经济、管理、自动控制等领域应用广泛[11-13],备受关注。虽然确定性微分博弈向不确定随机微分博弈的过渡是项艰巨的任务,但却是更符合客观实际的。随着时间的推进,微分博弈的相关研究已从一般系统扩展到奇异随机系统、Markov跳变系统等更为复杂的系统。
Moon等研究了马尔可夫跳跃系统线性二次随机零和微分博弈的充分条件[14]。Zhou等用配方法研究了连续时间和离散时间奇异随机系统的线性二次微分博弈问题,得到均衡策略存在的条件[15-16]。Mukaidani等给出了奇异随机系统的Pareto策略及其数值求解算法[17]。Song等研究了Markov跳变系统二人零和微分博弈均衡策略[18]。Zhang等系统的研究了线性Markov跳变系统连续时间和离散时间下的Nash博弈均衡策略,并给出了其在金融保险中的应用[19]。Cao等研究了连续时间奇异随机Markov跳变系统的Nash博弈问题,给出了N人Nash均衡策略存在的条件及其显式表达式[20]。纵观上述文献,关于随机奇异系统、Markov跳变系统微分博弈问题已有一定成果,而关于奇异Markov跳变系统随机微分博弈问题的研究还处于起步阶段。
基于此,本文对离散奇异随机线性Markov跳变系统的N人Nash博弈问题进行分析,得到有限时间和无限时间下Nash均衡策略存在的条件及显式表达式,并将所得结果应用于随机H2/H∞控制问题。本文讨论N人博弈问题,相较于两人博弈问题,实际应用范围更广且更具一般性;其次,讨论的受控系统为离散奇异随机Markov跳变系统,充实了微分博弈的理论研究;最后,将所得结果应用现代鲁棒控制中的随机H2/H∞控制问题,丰富了微分博弈的应用研究。
2 预备知识
考虑一类离散奇异随机线性Markov跳变系统:
{Ex(t+1)=A(rt)x(t)+C(rt)x(t)w(t),
x(0)=x0∈n
(1)
其中,x(t)∈n是状态变量,w(t)是在给定的完备概率空间(Ω,F,P)上的实随机变量序列,且满足ε(w(t))=0和ε(w(t)w(s))=δts,δts为克罗内克算子。rt是一个取值于状态空间Ξ={1,2,…l}的离散时间Marko过程,其转移概率为Pr{rt+1=j/rt=i}=πij,转移概率矩阵为Λ={πij}l×l,其中πij≥0且对于任意的i,j∈Ξ满足和w(t)相互独立。(x0,r0)∈n×Ξ是初始状态,E∈n×n是给定的奇异矩阵,rank(E)≤n,A(rt)、C(rt)为适维常数矩阵,当rt=i(i∈Ξ)时,A(rt)=A(i),C(rt)=C(i)。
为保证系统(1)解存在的唯一性,给出下述引理1。
引理1[21]对所有的i∈Ξ,如果存在一对非奇异矩阵U(i),V(i)使得对三元组式(E,A(i),C(i))满足下述条件之一,则系统(1)存在唯一解。
(2)
其中A1(i),C1(i)∈r×r,C2(i)∈r×(n-r),C3(i)∈(n-r)×(n-r)。
其中Nn2(i)∈n2×n2是幂零的,且n1×n1,C2(i)∈n1×n2,n1+n2=n。
定义1[22]离散奇异随机Markov跳变系统(1)是:
(Ⅰ) 正则的,如果对所有的i∈Ξ,det(sE-A)不恒为0;
(Ⅱ) 无脉冲的,如果对所有的i∈Ξ,deg(det(sE-A))=rank(E);
(Ⅲ) 均方稳定的,如果对任意的初始条件(x0,r0)∈n×Ξ,都有
(Ⅳ) 均方容许的,如果它是正则,无脉冲和均方稳定的。
引理2[21]离散奇异随机Markov跳变系统(1)是均方容许的,如果存在矩阵P(i)=P′(i),使得对每一个i∈Ξ,下式成立:
E′P(i)E≥0,
(3)
3 有限时间N人Nash博弈
3.1 问题描述
考虑以下离散奇异随机线性Markov跳变系统:
(4)
其中,x(t)∈n表示状态变量,uk(t)表示博弈人k(k=1,2,…,N)的控制策略,其容许策略空间记为Uk。w(t)是实随机变量序列,且满足ε(w(t))=0和ε(w(t)w(s))=δts。rt是一个取值于状态空间Ξ={1,2,…,l}的Markov过程,rt和w(t)相互独立。当rt=i,i∈Ξ时,系数矩阵A(t,rt)=A(t,i),A1(t,rt)=A1(t,i),Bk(t,rt)=Bk(t,i)。
对于博弈人k,其性能指标取经典的线性二次型:
(5)
当rt=i,i∈Ξ时,Rk(t,rt)=Rk(t,i)≥0∈Snk,Qk(t,rt)=Qk(t,i)≥0∈Sn;当rT=i时,Mk(rT)=Mk(i)≥0∈Sn。
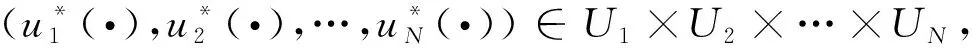
我们将研究限定博弈人的控制策略均为线性状态反馈情形,即uk(t)=Kk(t,rt)x(t),其中Kk(t,rt)是适维矩阵。
3.2 主要结论
利用配方法,我们给出上述有限时间N人随机Nash博弈问题均衡策略的显式表达和最优性能指标值。
定理1如果下述差分方程组(6)存在解Pk(t,rt)=Pk(t,i)∈Sn(i,j∈Ξ),
(6)
其中
则有限时间内,系统(4)-(5)的N人博弈问题的Nash均衡策略集存在,其显式表达式为
(7)
且最优性能指标值为
(8)
证明考虑任一博弈人k的最优策略,其面临的最优化问题为
s.t.Ex(t+1)=A-k(t,rt)x(t)+Bk(t,rt)uk(t)+A1(t,rt)x(t)w(t)
(9)

从而有:
(10)
(11)
对式(11)中的加和项进行配方,得
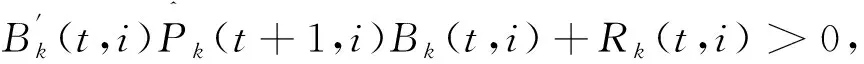
(12)
此时,最优控制策略和最优性能指标值如式(7)和(8)所示。
4 无限时间N人Nash博弈
4.1 预备知识
首先介绍无限时间随机最优控制中的一个重要概念——随机稳定性。
考虑如下离散奇异随机Markov跳变系统:
Ex(t+1)=A(rt)x(t)+B(rt)u(t)+A1(rt)x(t)w(t),t=1,2,…
(13)
其中,x(t)∈n是状态变量,u(t)是容许控制过程,w(t)是实随机变量序列,且满足ε(w(t))=0和ε(w(t)w(s))=δts。
定义2[23]给定任意初始状态x(0)=x0,r0=i,系统(13)是(均方意义下)随机稳定的,如果存在一个反馈控制u(t)=K(i)x(t)(i∈Ξ),其中K(i)均为常数矩阵,使得闭环系统Ex(t+1)=[A(rt)+B(rt)K(rt)]x(t)+A1(rt)x(t)w(t)是渐近均方稳定的,即limt→∞ε[‖x(t)‖2]=0。
需要注意的是,与有限时间情形相比较,无限时间情形的不同之处表现为
(ⅰ) 系统(13)是时不变的且性能指标中的权重矩阵为常数;
(ⅱ) 当T→∞时,Mk(rT)=0;
(ⅲ) 要求系统(13)是均方稳定的。
4.2 主要结论
考虑式(14)所示的奇异线性Markov跳变系统:
(14)
其中,x(t)∈n是状态变量,uk(t)是第k(k=1,2,…,N)个容许控制过程,表示博弈人k的控制策略,其容许策略空间记为Uk。w(t)是实随机变量序列,且满足ε(w(t))=0和ε(w(t)w(s))=δts。rt是取值于状态空间Ξ={1,2,…,l}的Markov过程,rt和w(t)相互独立。当rt=i(i∈Ξ)时,系数矩阵A(rt)=A(i),A1(rt)=A1(i),Bk(rt)=Bk(i)为适维常数矩阵。对于任一博弈人k,其性能指标取经典的线性二次型:
(15)
当rt=i(i∈Ξ)时,Rk(rt)=Rk(i)≥0∈Snk,Qk(rt)=Qk(i)≥0∈Sn。

∈U1×U2×…×UN,使下式成立:
同样地,我们将研究限定博弈人的控制策略均为线性状态反馈情形。
假定1[20]系统(14)是均方可稳的。
利用配方法,得到无限时间离散随机奇异Markov跳变系统N人Nash博弈问题的均衡策略如定理2所示。
定理2在假定1成立的基础上,若如下代数方程组(16)存在解Pk(rt)=Pk(i)∈Sn(i,j∈Ξ),
(16)
其中,
则无限时间内,系统(14)-(15)的N人博弈的Nash均衡策略集存在,其显式表达式为
且最优性能指标值为
定理2的证明过程与定理1类似,此处不再赘述。
5 应用于随机H2/H∞控制
现代鲁棒控制理论越来越广泛应用于工程实践及社会科学领域,随机H2/H∞控制获得广泛关注[17]。近年来,将Nash博弈方法应用于H2/H∞控制问题,成为了一种有效的方法[24]。其基本思路是将控制策略设计者和随机干扰性(不确定性)视为博弈的双方,H2/H∞控制问题就是控制策略设计者如何在预期到各种随机干扰(不确定性)策略情况下设计自己的策略,在实现与随机干扰性(不确定性)均衡的同时又使自己的目标最优,这样就可以把H2/H∞控制问题转化成Nash博弈问题[24-25],利用Nash均衡策略得到相应的鲁棒控制策略。
本部分拟将前文所得结果应用于离散奇异Markov跳变系统的随机H2/H∞控制问题。为分析简单,本文仅探讨有限时间情形,无限时间情形可类似分析。
考虑如下的受控系统:
(17)
受控输出:
式中,x(t)∈n是状态变量,uk(t)是第k个容许控制过程,v(t)表示外界干扰。当rt=i(i∈Ξ)时,系数矩阵A(t,rt)=A(t,i),A1(t,rt)=A1(t,i),Q(t,rt)=Q(t,i)≥0,Bk(t,rt)=Bk(t,i),Qk(t,rt)=Qk(t,i)≥0。rt和w(t)相互独立,v(t)和w(t)互不相关,且初始值r0与w(t)相互独立。其他符号含义如上文。L2(Ω,n)表示n值平方可和随机向量空间。l2(NT,q)表示所有有限序列y(t)构成的空间,其中y(t)∈L2(Ω,q)且对t∈NT是可测的,空间l2(NT,q)满足
下面给出有限时间随机H2/H∞控制的定义:
定义3[25]对于任意给定的γ>0,0 (ⅰ) ∀v(t)≠0∈l2(NT,v),初始状态x(0)=x0∈n的闭环系统(17)的状态过程满足: (ⅱ) 当最坏干扰v*(t)∈l2(NT,v)存在时,把v*(t)代入系统,同时使性能泛函 ‖uk(t)‖2]达到最小。 引入表示干扰抑制水平的标量γ>0,定义如下性能指标: 根据定理1,可得有限时间随机H2/H∞控制的最优策略以及最坏干扰的结果如定理3所示。 定理3对系统(17),如果下述差分方程组存在解Pk(t,rt)=Pk(t,i)∈Sn,P(t,i)∈Sn(i,j∈Ξ) 针对噪声依赖于状态与控制的离散奇异随机Markov跳变系统,分别讨论其在有限时间和无限时间情形下的N人Nash博弈问题,得到均衡解存在的条件及显式表达式,并将所得结果应用于相应的H2/H∞控制问题,得到了最优策略存在的条件,充实了微分博弈理论和应用研究。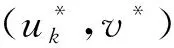
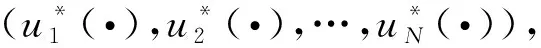
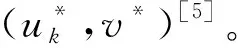
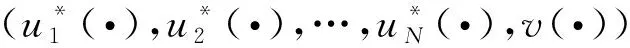
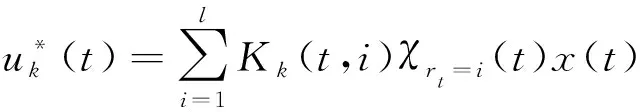
6 结论
