掺铒光纤激光器的动力学分析及电路实现

汪 杰 洋， 齐 兴 华， 刘 俊 俏， 马 晨 光

( 1.大连工业大学 信息科学与工程学院， 辽宁 大连 116034；2.大连工业大学 管理学院， 辽宁 大连 116034 )

0 引 言

混沌是一种普遍存在于自然界中的运动状态，对初始条件敏感，变化具有随机性，长期行为具有不可预测性。其宏观上虽呈现出无规则的状态，但其本质是一种有序运动[1-3]。混沌在各个领域皆有应用，例如图像与文字加密[4]；微弱分析与检测中的添加白噪声、高斯噪声[5]；机电耦合中的电机控制系统、换能系统与风电转换系统等[6-7]。研究者根据混沌系统的特性建立起对应的动力学方程，并通过软件仿真，硬件实现等手段对其进行研究，如Ruelle与Takens在研究奇怪吸引子的基础上，提出湍流理论，成为混沌实现的重要基础理论[8]。混沌电子电路的硬件实现是研究中的一种重要手段，是非线性科学中的一门前沿课题，其理论主要起源于对Lorenz系统和Chua系统的电路设计和研究[8-10]。

光纤激光器的介质材料通常使用掺杂少量稀土元素的光纤。作为一种典型的固体激光器，其大多利用光泵浦作为激发源(用1束强光照射激光器的基质材料，激励原子使其跃迁到更高的能级)，当泵浦光耦合到光纤中时，容易在直径较小的光纤中形成高功率密度，发生粒子数反转，进而与光学谐振器配合产生激光振荡。相比于其他种类光纤，掺杂铒离子的光纤在低损耗第三通信窗口具有更高的增益[11]。得益于其性质特点，掺铒光纤激光器具有可用带宽较宽、与光纤元件兼容性好、信噪比高以及与光纤通信最低损耗窗口相匹配等特点[12]。铒离子的亚稳态寿命最高可达10 ms，并且光纤芯功率密度高，使用掺杂铒离子的光纤作为激光介质的激光器对光信号具有放大作用并且可以由连续工作状态过渡到混沌状态[13-14]。光纤激光器是一种非线性系统，根据Arecchi以弛豫时间作为标准的分类方式可分为A、B和C三类[15]。其中A类和B类产生混沌的方式是引入一个新的自由度，而C类激光器不需要引入自由度便可以独立产生混沌行为[16]。本研究所使用的单模双环掺铒光纤激光器是一种以掺铒光纤作为基质材料的激光发生装置，是一种C类激光器[17]。

1965年，Snitzer完成了掺铒光纤激光器的硬件实现。自1985年，南安普顿大学对掺铒光纤的研究取得巨大进展后，研究人员开始对掺铒光纤激光器的动力学特征从理论和实验进行研究[18-21]。掺铒光纤激光器产生混沌的方法主要有：利用双环耦合作用；利用非线性克尔效应进行泵浦或损耗调制；利用高掺杂光纤中的铒离子对作用等[22-23]。本研究利用双环耦合作用，将两个单环掺铒光纤激光器耦合，使其产生混沌现象。单模双环掺铒光纤激光器混沌行为的研究需要投入较高的成本，现阶段尚未出现对其进行系统全面的研究。本研究所提出的模拟电路可以表现出与单模双环掺铒光纤激光器相同的动力学行为，其简单的电路结构为激光器混沌行为的分析提供了一种新的研究方法。

1 系统原理

单模双环掺铒光纤激光器由两个掺铒光纤激光器耦合而成，其表现出的非线性动力学特征由激光器中两激光场的实部和虚部正交偏振的耦合效应所产生，结构原理如图1所示。单环掺铒光纤激光器a和激光器b通过定向耦合器M0形成一个三能级激光器系统。Ipa，Ipb分别为两个环的泵浦场强，Ea，Eb分别为两激光器归一化输出激光场强度。Wdm为波分复用器，能将部分谐振腔内的激光耦合到谐振腔的外部，同时将多种波长的泵浦光耦合到掺杂了铒离子的介质光纤中。当激光器内部的激光强频率锁定后，a环与b环中的激光光场通过耦合器M0实现互通。

单模双环掺铒光纤激光器是三能级激光系统，所以激光在通过耦合器M0会产生相位变化。通过对其反转粒子数和输出激光场的动力学行为进行分析，可以得到其动力学方程，一个新的四维自治动力学方程组，如式(1)所示。

(1)

式中：Da，Db分别为激光器a和激光器b的反转粒子数；kα，kβ分别为激光器a和激光器b的损耗系数；gα，gβ分别为激光器a和激光器b的增益系数；δ0是光耦合器的耦合系数。

对式(1)进行无量纲处理，令ka=a，δ0=b，gα=c，kb=d，gβ=e，Ipa=l，Ipb=g，得到式(2)所示无量纲方程。

(2)

单模双环掺铒光纤激光器中的耦合项存在非线性耦合效应，可以通过改变参数使系统以倍周期方式进入混沌状态，稳定表现出混沌系统的特征。以最大李雅普诺夫指数L1作为判断依据，当L1>0时，系统处于混沌状态，在对其进行分析后确定混沌态时的系统参数。

设无量纲化动力学方程中的各项参数为a=8.2，b=0.2，c=10，d=10，e=5，g=5，h=5，计算出该参数条件下4个李雅普诺夫指数为L1=0.122 7，L2=-0.014 4，L3=-0.566 4，L4=-0.966 7。系统相图如图2所示。

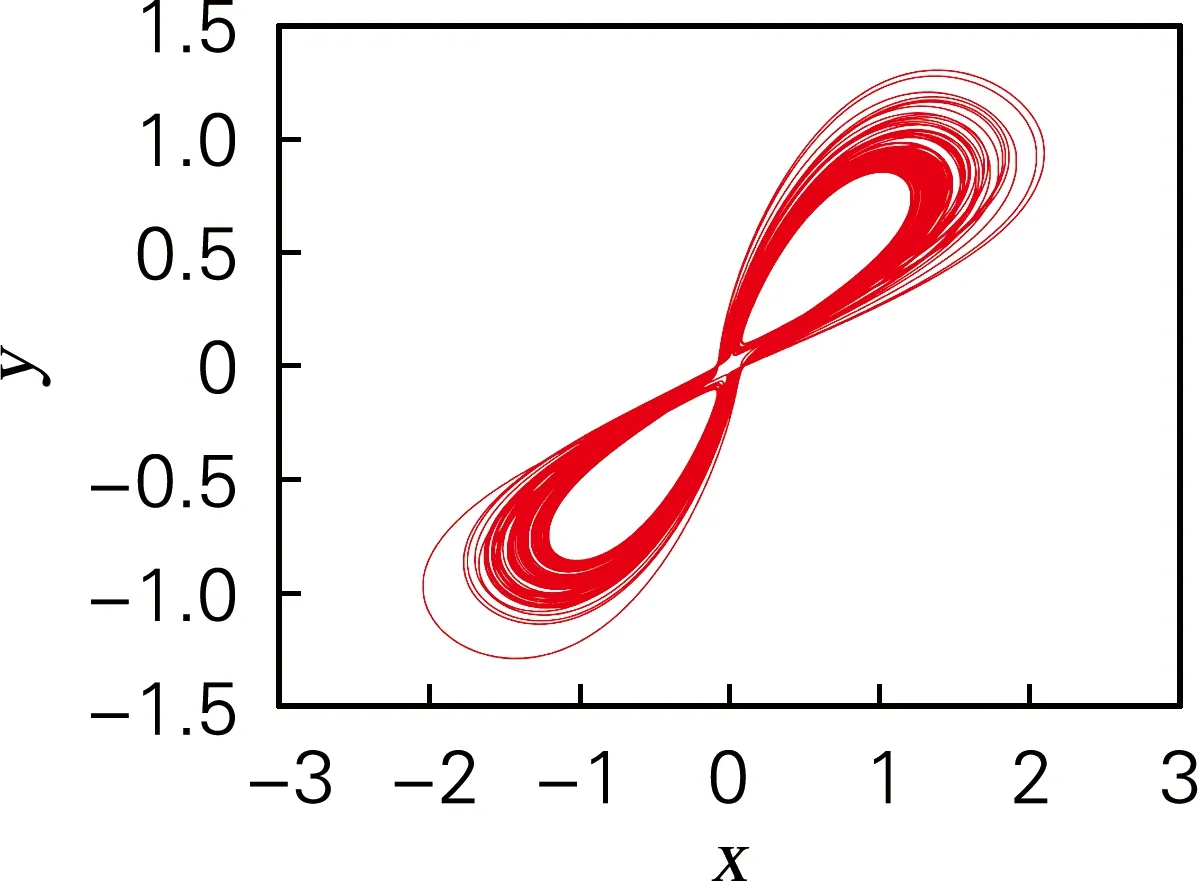
(a) x-y平面相图

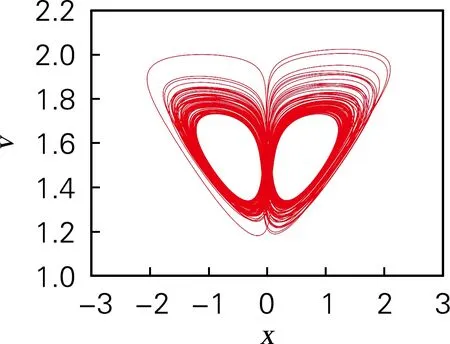
(b) x-v平面相图

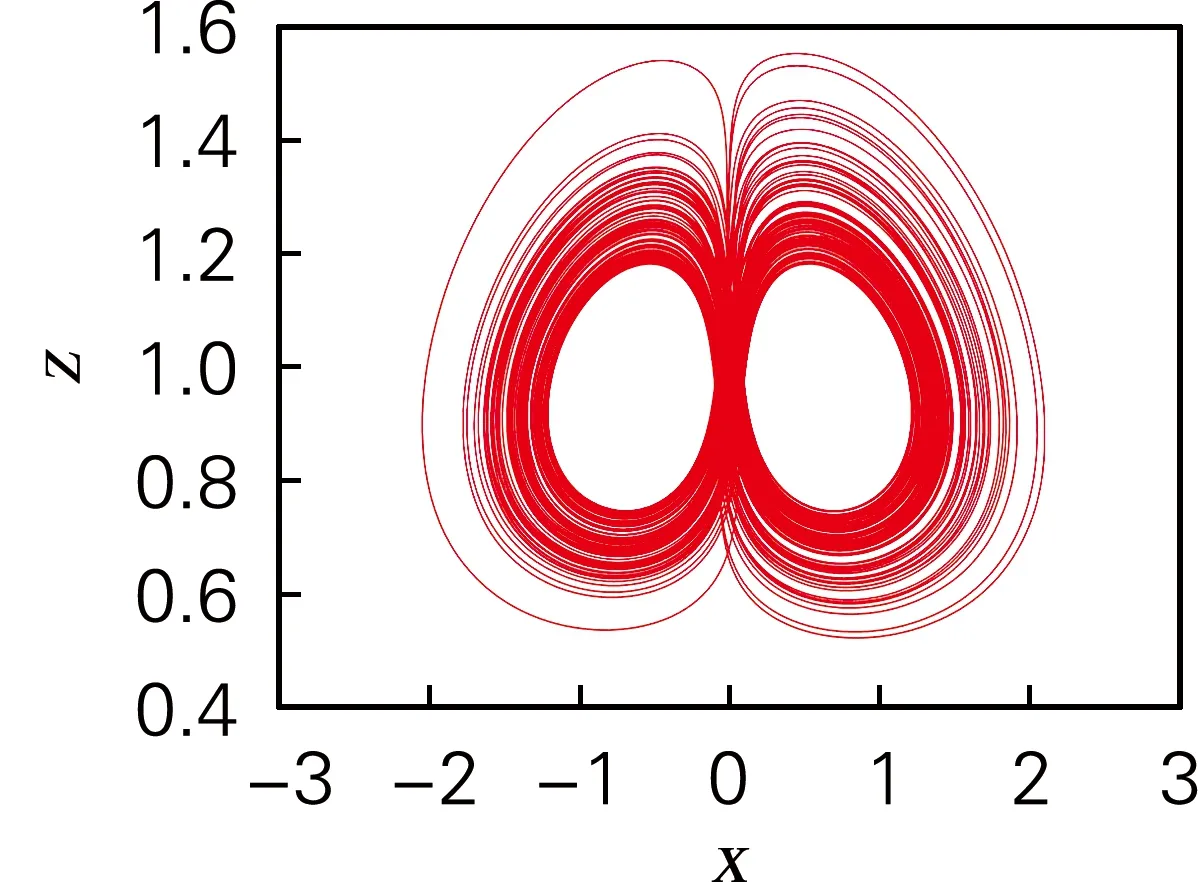
(c) x-z平面相图

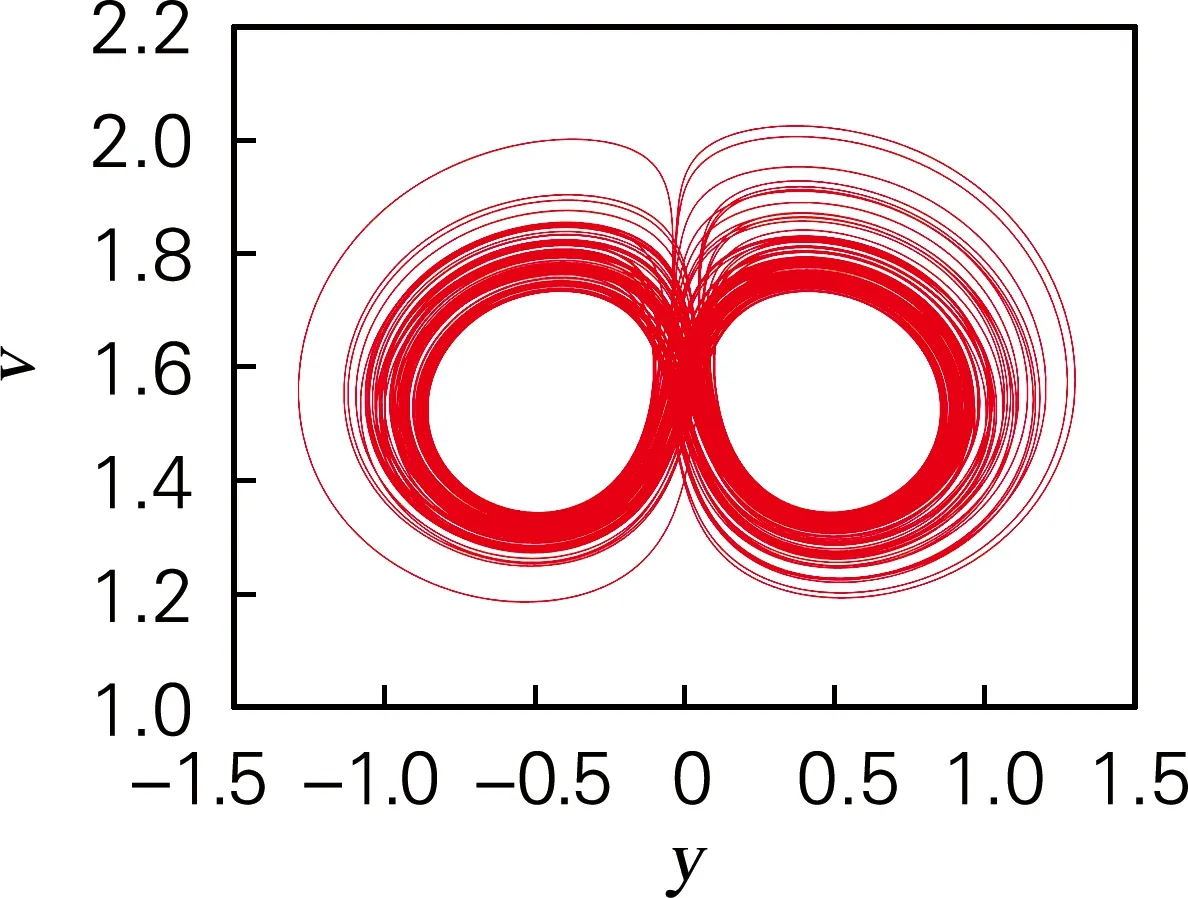
(d) y-v平面相图

2 系统动力学分析

2.1 系统的平衡点分析

令动力学方程组式(2)各项等于0，得到系统的3个平衡点为S1(0，0，6.666 7，6.666 7)，S2(-0.602 7，-0.459 5，0.945 0，1.475 3)，S3(-0.602 7，-0.459 5，0.945 0，1.475 3)。

在平衡点Sj(x，y，z，v)(j=1，2，3)处线性化得到其Jacobian矩阵，如式(3)所示。

(3)

Jacobian矩阵特征多项式为

f(λ)=A4λ4+A3λ3+A2λ2+A1λ+A0

式中：

A4=1

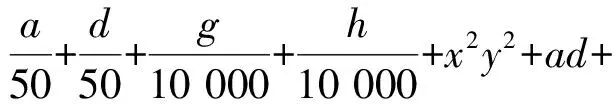
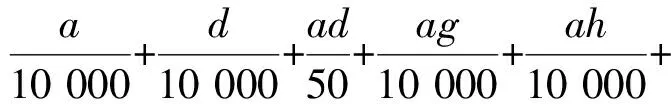
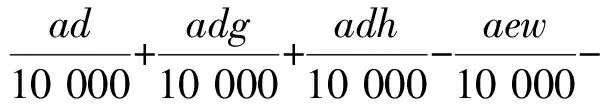
根据劳斯-赫尔维茨判据，若平衡点稳定，应满足条件

经计算，当系统参数取a=8.2，b=0.2，c=10，d=10，e=5，g=5，h=5时，S1，S2和S3都为不稳定的平衡点。

2.2 系统的分岔图及李雅普诺夫指数谱

以参数a和d作为变量，分别对应单模单环掺铒光纤激光器a的损耗系数kα与光耦合器的耦合系数δ0。设定系统初值为(0.1，0.1，0.1，0.1)，取步长为h=0.01，固定方程的剩余参数，比较不同参数下的状态。

取a∈[7，12]，令a=8.2，b=0.2，c=10，d=10，e=5，g=5，h=5，李雅普诺夫指数谱和分岔图如图3所示。由图3可知，当a∈[7.0，7.4]时，最大李雅普诺夫指数L1小于0，系统此时表现为周期窗口。当a∈[7.4，11.4]时，最大李雅普诺夫指数L1始终大于0，并且没有其他指数大于0，所以这时系统表现出混沌状态。a∈[11.4，12.0]时，4个李雅普诺夫指数L1、L2、L3和L4均小于0，系统此时表现为稳定状态。

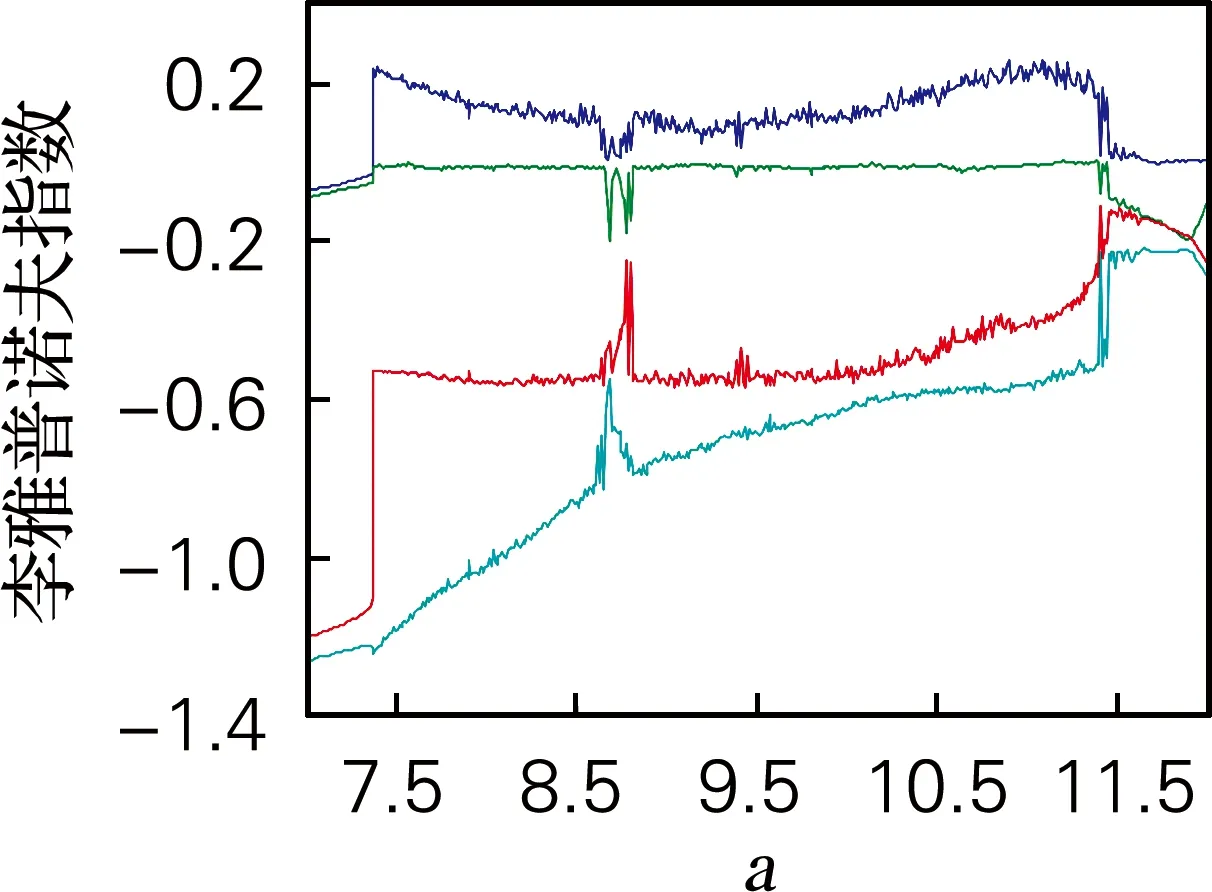
(a) 李雅普诺夫指数谱

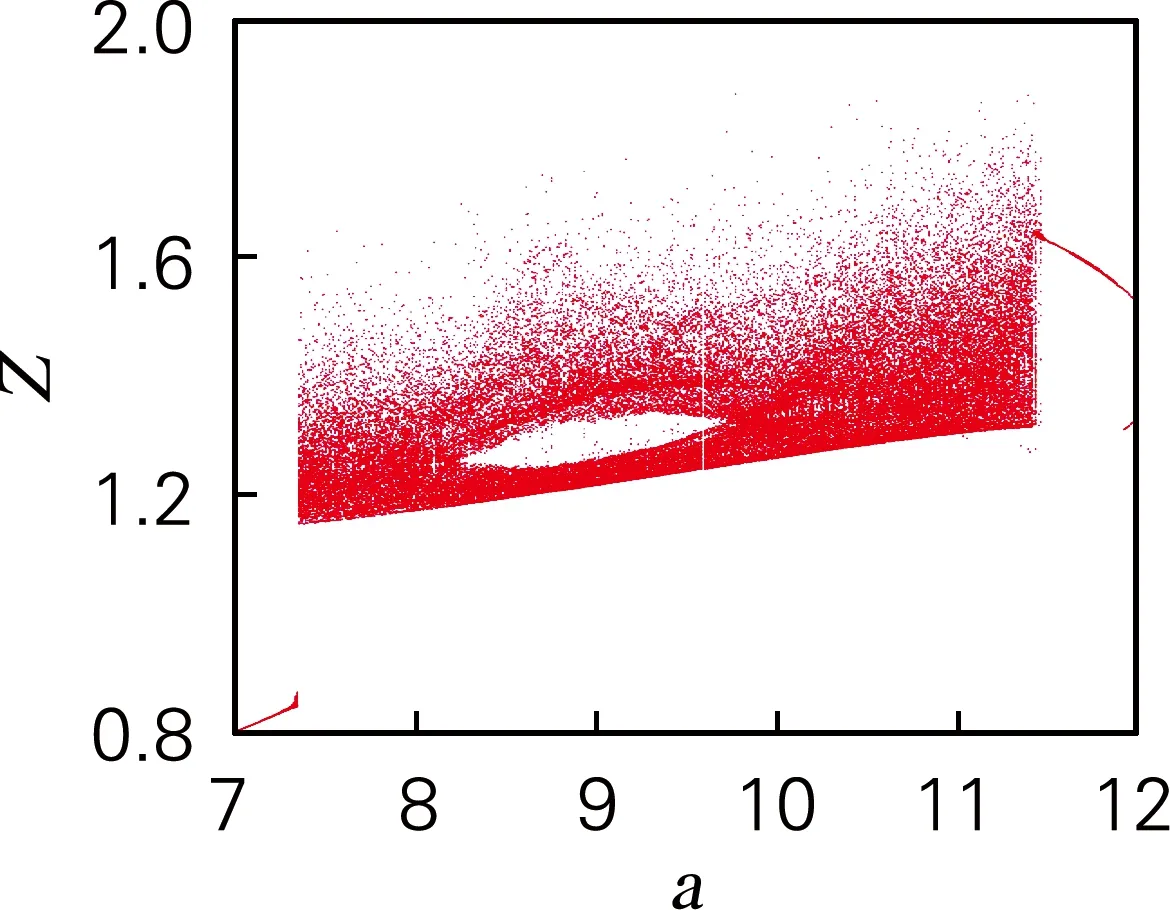
(b) 分岔图

随着a的增大，系统由周期态演变成混沌态又退化为稳定的极限环。图4分别示出当参数固定取b=0.2，c=10，d=10，e=5，g=5，h=5，a分别取7.0，8.2和11.5时系统的x-y平面相图。当a=7.0时，相图为周期状态，由李雅普诺夫指数谱可知，此时系统的4个指数均小于0，系统处于周期状态；当a=8.2时，相图为混沌状态，此时系统的3个指数小于0，一个大于0，系统处于混沌状态；当a=11.5时，相图为极限环状态，此时系统的3个指数小于0，一个等于0，系统处于极限环状态，分析可知，相图与分岔图和李雅普诺夫指数谱完全对应。

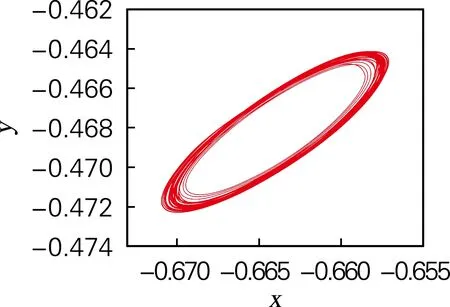
(a) a=7.0

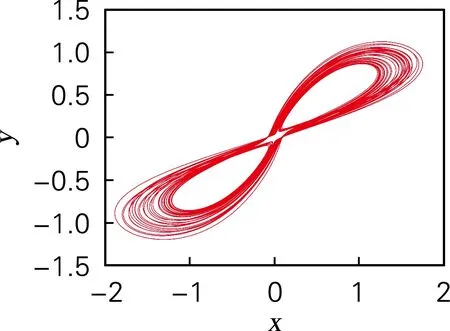
(b) a=8.2

(c) a=11.5图4 系统以a为变量的x-y平面相图Fig.4 The x-y phase diagrams when system takes a as variable

取d∈[7，12]，a=8.2，b=0.2，c=10，e=5，g=5，h=5，该条件下李雅普诺夫指数谱和分岔图如图5所示。当d∈[7.0，7.6]时，最大李雅普诺夫指数L1等于0，系统此时表现为极限环。当d=7.7时，系统开始出现倍周期分岔现象。当d∈[7.8，11.5]时，最大李雅普诺夫指数L1大于0，并且没有其他指数大于0，此时系统表现出混沌状态。当d∈[11.5，12.0]，4个李雅普诺夫指数L1，L2，L3和L4均小于0，系统此时表现为稳定的周期态。

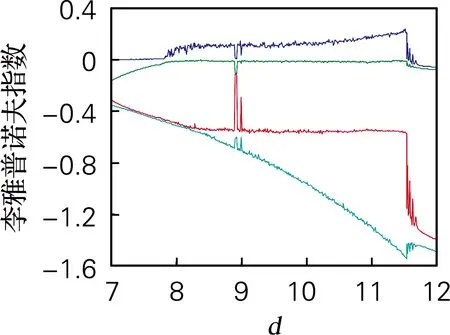
(a) 李雅普诺夫指数谱

图6为a=8.2，b=0.2，c=10，e=5，g=5，h=5，d分别取7.5，8.1和11.5的x-y相图，当d=7.5时，相图为极限环，由李雅普诺夫指数谱可知，此时系统的3个指数小于0，一个等于0，系统处于周期状态；当d=8.1和d=11.5时，相图均为混沌状态，此时系统的李雅普诺夫指数均为3个小于0，一个大于0，处于混沌状态，不同的是，在d=11.5时，最大李雅普诺夫指数远大于d取8.1时，此时系统表现出的混沌特性要远高于d=8.1时。该结果与图5所示分岔图与李雅普诺夫指数谱完全对应。

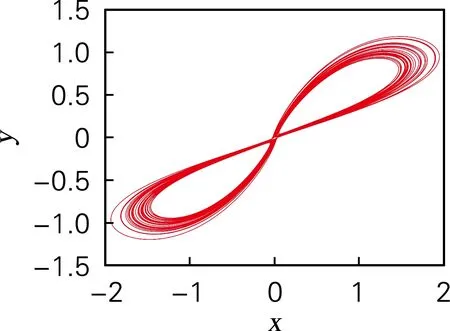
(c) d=11.5

2.3 系统复杂度分析

混沌系统的复杂性表示系统与随机序列的接近程度，其复杂度大小是待测序列随机程度的表征。

复杂度分析包含行为复杂度和结构复杂度，两种分析方法在变化趋势上具有一致性。行为复杂度大多使用ApEn，SampEn和FuzzyEn等算法，这类算法在处理短数据和连续数据时，能达到很好的衡量效果，但当数据变长时，计算速度就会明显下降。结构复杂度在处理长数据时具有较好的表现，本研究将利用SE算法和C0算法对结构复杂度进行分析。

SE(谱熵)算法主要采用傅里叶变换，通过傅里叶变换域内能量分布，结合香农熵得出谱熵值。C0算法主要思想是将序列分解为规则和不规则部分，对其中非规则部分比例进行测量得到结果。

本研究以参数a作为变量对系统的复杂度进行分析，其他参数取值：b=0.2，c=10，d=10，e=5，g=5，h=5。a∈[7，12]时仿真结果如图7所示。

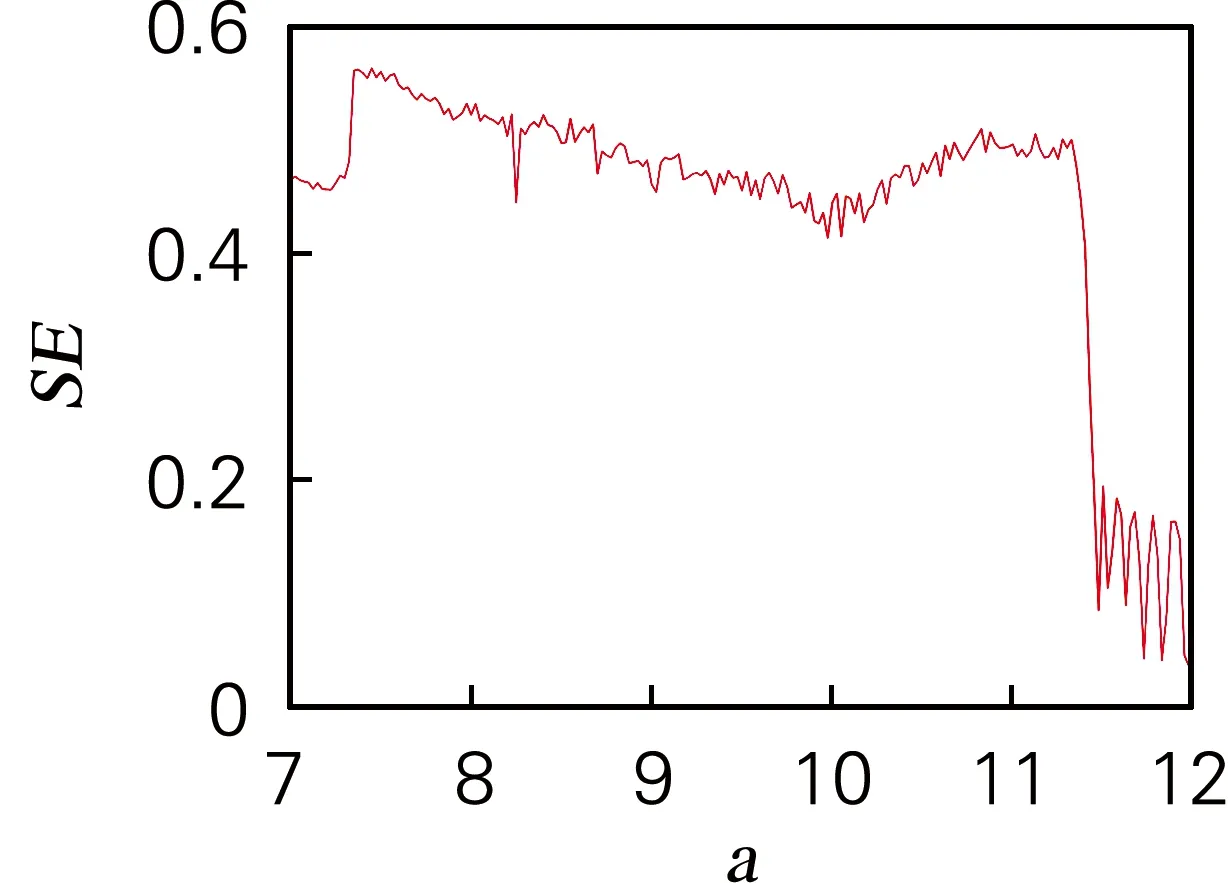
(a) SE复杂度

(b) C0复杂度

由图7可知，SE算法和C0算法具有高度的同步性，当a<7.4时，系统处于周期状态，当a∈[7.4，11.4]时，系统处于混沌状态，当a>11.4 时，系统退化为极限环状态。通过分析SE复杂度图和C0复杂度图可以发现，当系统处于周期态时复杂度处于低点，当系统进入混沌态时复杂度明显增大，所呈现出的结果与图3所示李雅普诺夫指数谱和分岔图相吻合。

3 电路设计与仿真

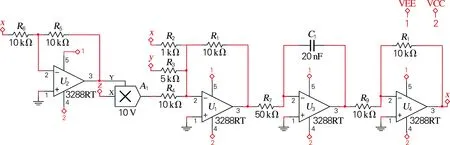
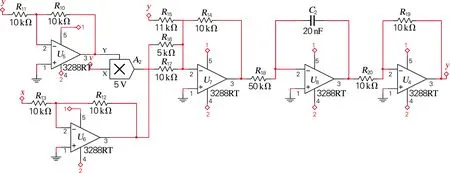
混沌理论在实际工程中往往需要物理实现。本研究根据单模双环掺铒光纤激光器系统的动力学方程组及电路理论设计出模拟电路模型，利用Multisim对其进行验证分析，模拟电路结构如图8所示。本电路采用线性电阻、线性电容、模拟乘法器和3288RT运算放大器等元器件。根据电子元件的基本逻辑功能，电路分别使用了反向加法比例运算电路，反向比例运算电路，反相器和反向积分器等利用运算放大器完成的模拟运算电路。该电路通过对输入信号(x，y，z，v)的加减运算，乘积运算，变号和积分运算表现出与单模双环掺铒光纤激光器相同的动力学特征。

图8电路中所示元件取值如表1所示。

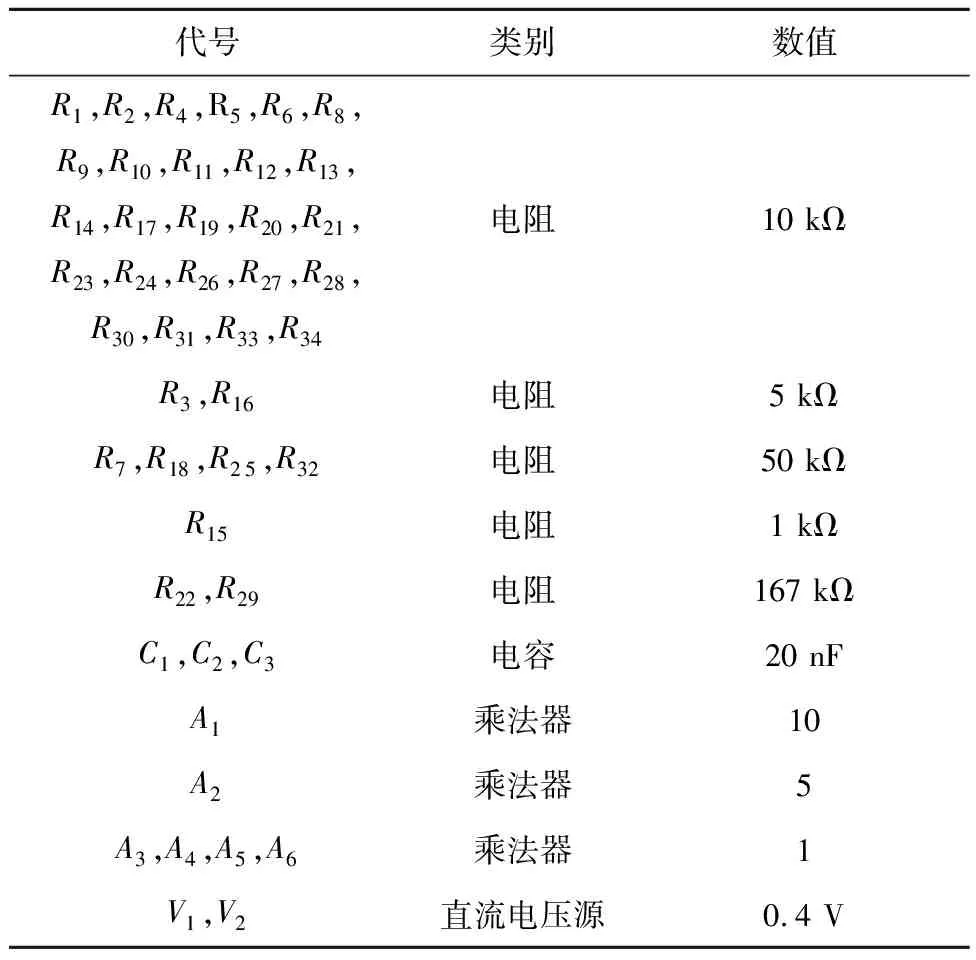
表1 电路元件取值表Tab.1 Circuit element value list

根据图8所示电路模型，使用Multisim进行搭建仿真，通过改变相应电阻的取值使系统状态改变，得到的x-y相图如图9所示，分别对应图6的3个相图。

4 系统DSP仿真

虽然单模双环掺铒光纤激光器的模拟电路可以实现，但在实际电路中相关特征条件较难准确控制，容易因为外部扰动产生误差。本研究在DSP平台上对本系统进行仿真，表现出的混沌现象将更加稳定。

所使用的DSP仿真芯片为f28335，设定参数a=8.2，b=0.2，c=10，d=10，e=5，g=5，h=5，得到如图10所示的图像。

固定参数a=8.2，b=0.2，c=10，e=5，g=5，h=5，取参数d作为变量，得到如图11所示的结果，分别对应参数d取7.5，8.1和9.5时的3个相图。

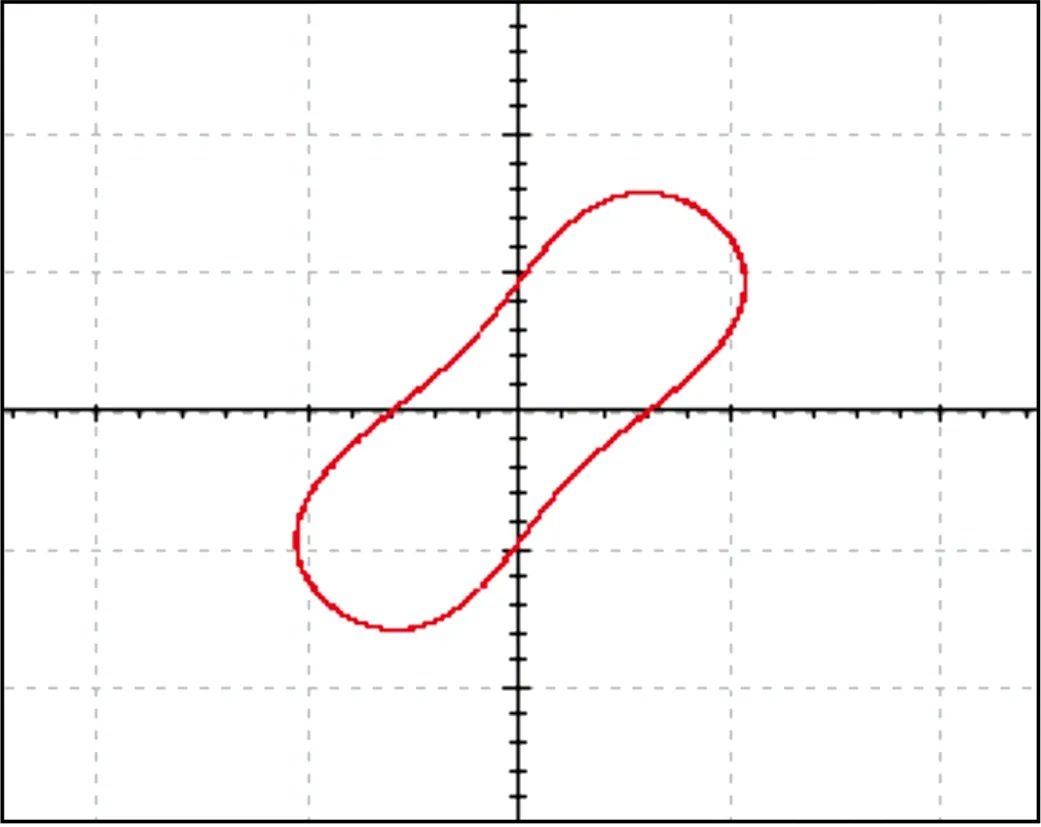
(a) d=7.5

(b) d=8.1

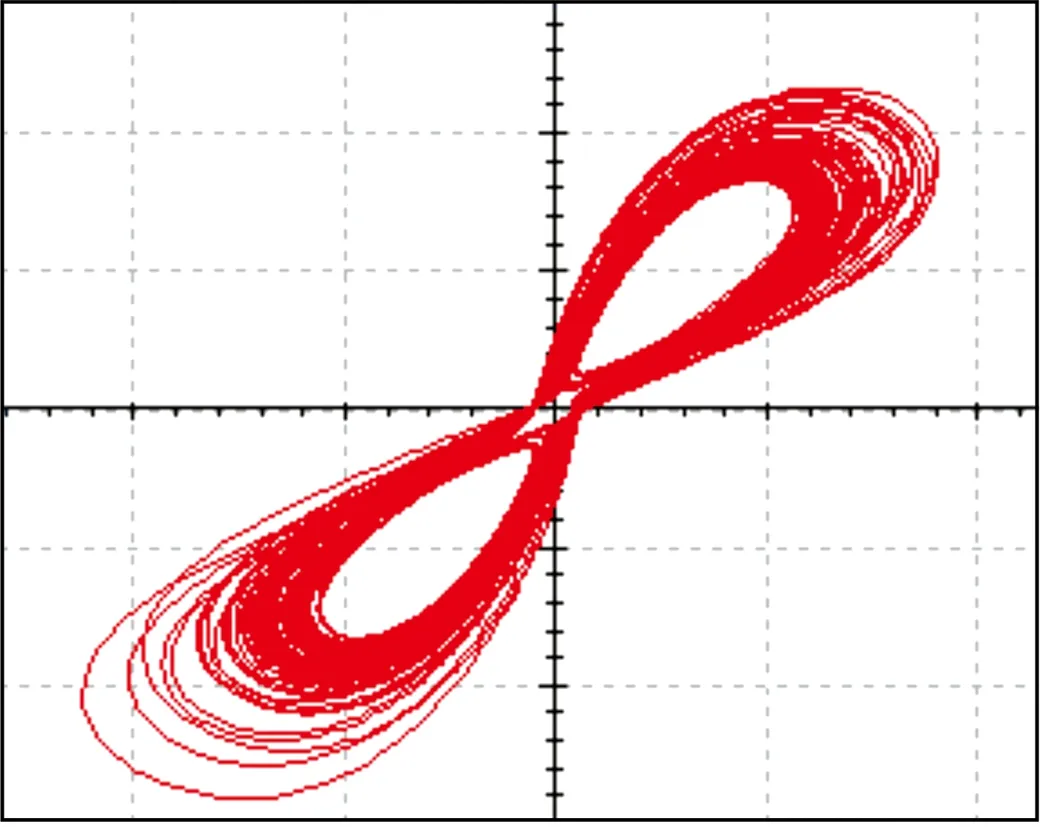
(c) d=11.5图9 系统随d变化的Multisim仿真x-y平面相图Fig.9 Multisim simulation x-y phase diagrams of the system changing with d

(c) x-z图10 DSP仿真各平面相图Fig.10 DSP simulation of the plane phase diagrams

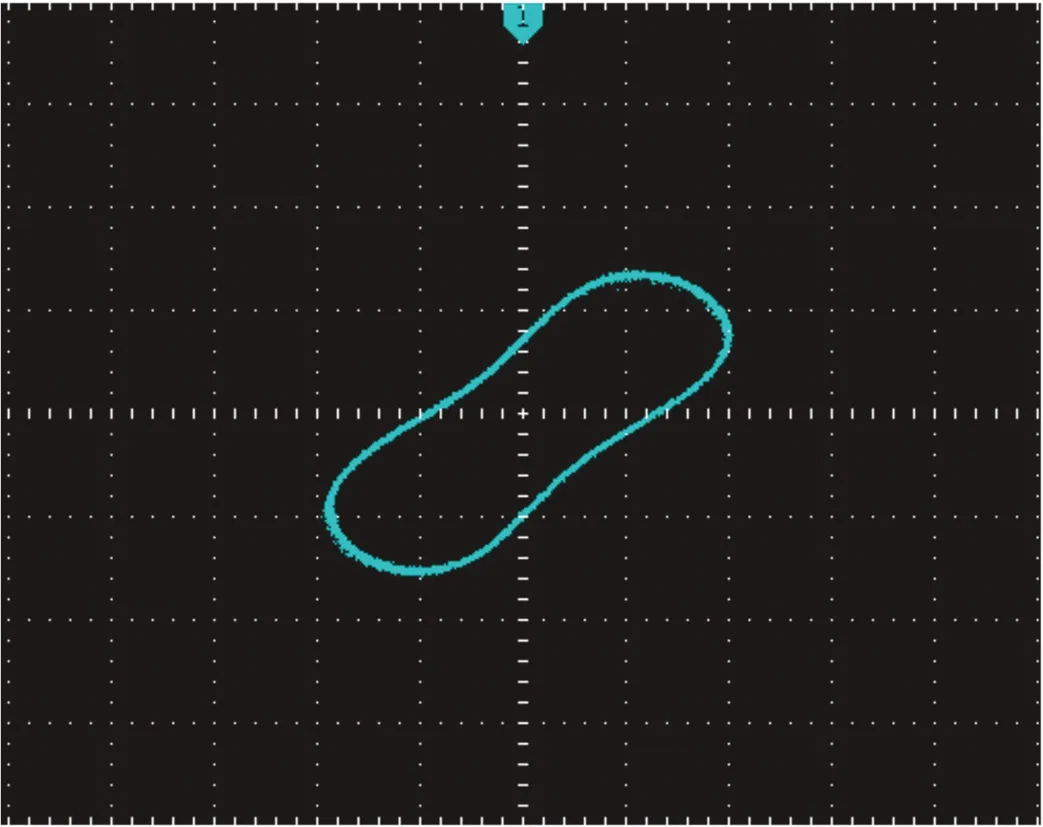
(a) d=7.5

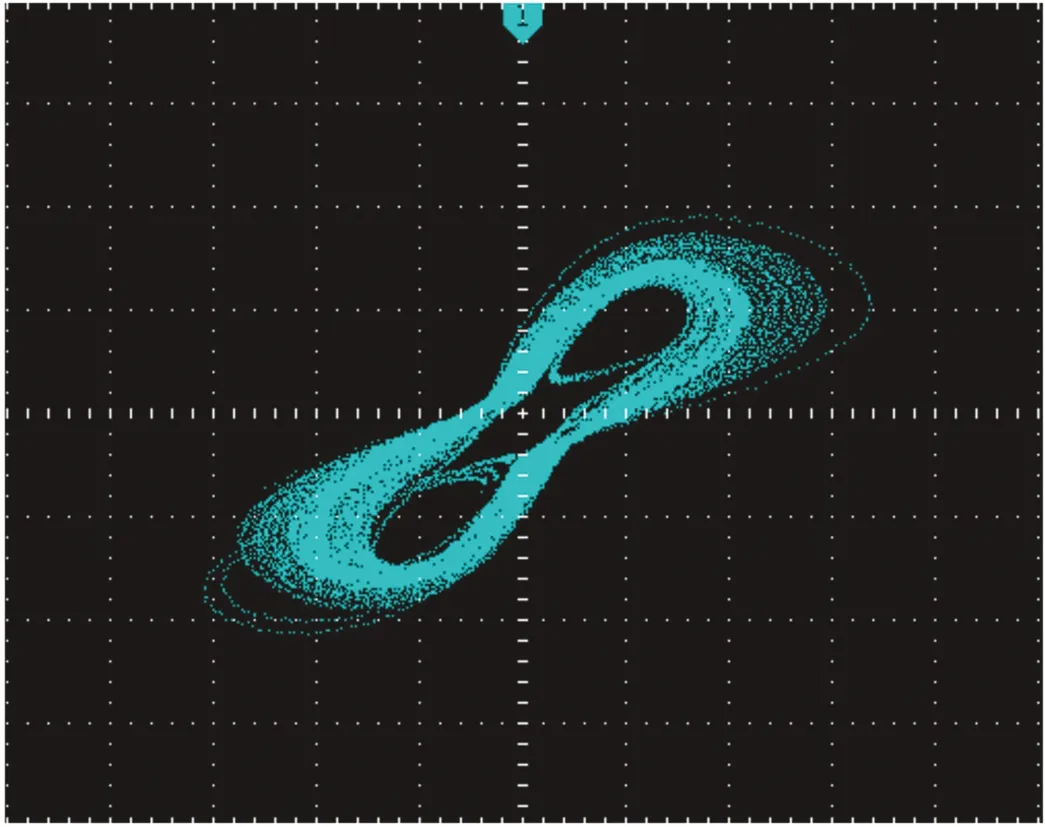
(b) d=8.1

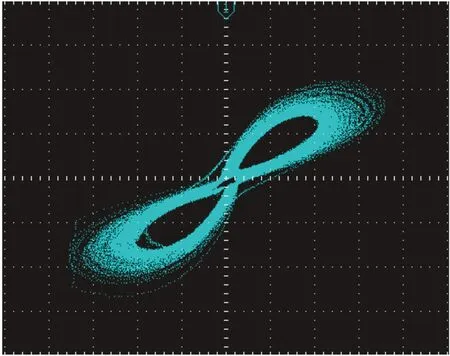
(c) d=11.5图11 系统随d变化的DSP x-y平面仿真相图Fig.11 DSP simulation x-y phase diagrams changing with d

系统DSP仿真所用的f28335芯片及示波器如图12所示。

图12 DSP仿真实物图Fig.12 The physical picture of DSP simulation

5 结 论

通过对单模双环掺铒光纤激光器进行分析，获得一组四维动力学方程。利用相图，分岔图和李雅普诺夫指数谱对本系统的动力学特征进行分析。结合电路原理设计出一套模拟电路，并利用Multisim和DSP平台对其进行验证。实验表明，单模双环掺铒光纤激光器系统在特定参数条件下能够表现出稳定的混沌现象。根据系统方程组设计出的模拟电路在元件取值设定合理的情况下，能实现单模双环掺铒光纤激光器同步变化。证实本模拟电路可以作为研究单模双环掺铒光纤激光器的辅助手段。本文的研究结果为单模双环掺铒光纤激光器的研究提供了新的思路，具有较高的应用价值。