从光的单缝衍射分析动量与坐标的不确定关系

[摘 要]如何理解不确定关系是量子力学教学中的难点之一，初学者对其存在一定困惑。文章从经典物理中易理解的光的单缝衍射条纹特点出发，进一步分析了量子力学中的不确定关系并展开讨论，助力学生对知识点的理解与掌握。

[关键词]光的单缝衍射;条纹特点;动量与坐标;不确定关系

[中图分类号] O 413.1 [文献标识码] A [文章编号] 2095-3437（2021）10-0112-03

量子力学作为近代物理两大支柱之一，其产生和发展都给经典物理学带来巨大的冲击与变革，几乎颠覆了以牛顿力学为代表的经典物理理论，也不断促使人们对物理的认识不断深入。可以说，现代物理学的分支及相关的边缘学科无一不是建立在量子力学基础之上的[1]。

一、从经典到量子的学习困惑

量子力学的研究对象主要是微观世界物质的运动，量子力学中许多概念与经典物理有着根本性的区别，相应的原理也自然不同， 如何“摆脱”经典物理思想去理解量子力学是学生面临的第一难题[2]。而且量子力学所包含的新概念、新思想与经典力学差别大。普遍认为量子力学提出的概念有悖于日常生活的物理直觉，初学者要抛弃原有经典物理的一些观点， 从不同角度重新理解自然界的本质[3]。量子力学中很多理论难以与从日常生活经验所得出的结论相对应，而且有些理念往往与现实生活所得到的结论相违背，要让学生在有限的时间内完成长期以来形成的经典物理理论向量子力学新理念的转变，无疑是很难做到的，加之在对其学习的过程中需要一定的数学功底，使得大部分学习此科目的学生感到困难和迷惑，甚至有的学生在学了一段时期量子力学后仍对所学知识持怀疑态度。如何在有限的时间内入门是初学者在由经典向量子过渡过程中遇到的瓶颈。不确定关系（又称测不准原理）是德国物理学家海森堡于1927年进行的量子物理实验得出，并因此获得了1932年的诺贝尔物理奖，这是由于微观粒子具有波动和粒子两重性，体现在量子力学中，一个微粒的某些物理量，不可能同时具有确定的数值，其中一个量越确定，另一个量的不确定程度就越大，这就是测不准原理[4]。坐标是描述物体位置的物理量，动量是指的物体的质量与其速度的乘积，是一个表示物质运动状态的物理量，在经典力学中，质点的动量与坐标是可以同时精确测定的，质点的动能、势能等其他物理量是坐标和动量的函数，只要坐标的动量有确定的值，其他物理量的值也就确定了。故在经典物理中，通常借助于质点的坐标和动量（或速度）来描述质点的运动状态。但对于微观世界而言，例如电子，同时测量其位置和动量却成为不可能。海森堡所提出的量子不确定性原理和矩阵力学奠定了现代量子力学坚实的基础，并凸顯了经典力学和量子力学的本质不同[5]。不确定关系作为量子力学基本原理作为量子力学的一个基本原理，原子零点振动的存在就充分认证了不确定关系的正确性。本文从经典物理中的光的单缝衍射出发，通过类比和推导的方式来分析坐标与动量的不确定关系，让学生更好地理解量子力学的这一基本原理。

二、单缝衍射条纹特点

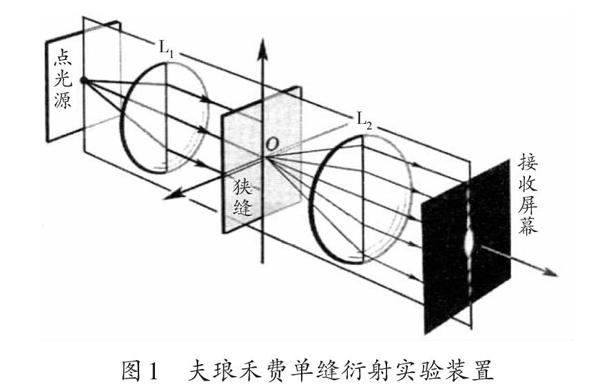
如图1所示，是在实验室中夫琅禾费衍射装置，其中L1和L2是两个凸透镜，接收屏幕位于透镜L2的焦平面处，点光源通过透镜L1折射后变为一束平行光，照在狭缝（衍射屏）上，狭缝开口处的波前向各个方向发出次波（衍射光线），方向相互平行的衍射光线在经过透镜L2后汇聚在其像方焦平面的同一点上。在研究这个问题上，常用的方法是利用菲涅尔的子波波源思想将波阵面分割成多个面积相等的波带，并且满足相邻波带对应的子波到观察点的光程差为半个波长（又称之为菲涅尔半波带法）。于是，偶数个半波带相互干涉的总效果，是在观察点相干减弱，使得观察点呈现暗纹中心;若波面被分为奇数个半波带，此时相邻两个半波带上各对应点的子波相互干涉抵消后，只剩下一个半波带的子波到达观察点时没有被抵消，因此观察点一般是明纹中心，其结论如下[6]：

暗纹中心满足： [Bsinθ=±2kλ2=±kλ，k=1，2，...] （1）         明纹中心满足：[Bsinθ=±2k+1λ2，k=1，2，3...]  （2）

通常情况下，单缝衍射条纹的衍射角很小，[sinθ≈tanθ]，则条纹在屏上距离中心的距离可表示为：                      [Y=ftanθ]                                                        （3）

由式（1）-（3）可得，中央明纹宽度：

[ΔY0=2λfB]                                                     （4）

其他明纹宽度： [ΔY=λfB]                               （5）

其中[B]为缝宽，[θ]为衍射角，规定竖直方向为[y]方向。

由式（5）可以看出，对于一定频率的入射光而言，缝宽与条纹宽度成反比，即：

[B↓→ΔY↑B↑→ΔY↓]                                                         （6）

这也与单缝衍射过程中所观察到的实验现象相吻合。在传统的教学中，学生对这一部分知识点的理解和掌握情况远好于“不确定关系”，相关调研情况如下：

表1和图2是所显示的是对一个76人的教学班级调查情况，从图表中的定量描述可以看出，采用如上所述的菲涅尔半波带法，构思非常巧妙，有效地避免了烦琐的数学推导，便能得出单缝衍射条纹的特点，学生易理解，掌握情况也较好;而按照传统的先后顺序对于不确定关系的授课效果就不乐观。

三、单缝衍射与不确定关系对比分析

为了让学生更好地理解坐标与动量的不确定关系，下面从单缝衍射的条纹特点出发，用类比的方法分析量子力学中坐标与动量的不确定关系。为了更加直观，我们用如图3表示的粒子单缝衍射光路，光粒子从位于凸透镜焦点处点光源O发出后经过凸透镜折射，成为平行光，并以确定的动量[P0]射向带有单缝的屏，单缝处于y方向，令狭缝的宽度

[B≡Δy]                                                                （7）

显然，式（7）决定了粒子坐标在狭缝屏上在y方向上的变动范围，在其后的观察屏出现的是衍射条纹，可以认为，观察屏上所显示的衍射条纹的宽度，所体现的是粒子在y方向上的动量[Py]的变化范围[ΔPy]，由式（6）可知，狭缝越窄（即[Δy]越小），衍射条纹的宽度就会越宽（即[ΔPy]越大）。对于一般的光的单缝衍射而言，其衍射角、波长和狭缝宽度均有如下关系：

[α≈λ2πB=λ2πΔy]                                                   （8）

其中，[λ2π]又称之为圆波长。

在衍射角不太大时，衍射角与入射粒子的动量[P0]及在[y]方向上的动量变化范围[ΔPy]的关系为：

[α≈ΔPyP0]                                                                   （9）

由德布罗依关系可得[7]：

[λ=hP0]                                                                   （10）

其中[h]为普朗克常数（[h≈6.626×10-34J?s]），由式（8）-（10），可得

[Δy?ΔPy≈h2π]                                                      （11）

通常情況下，如果把衍射图样的次级也纳入考虑范围之内，式（11）应修正为：

[Δy?ΔPy≥h2π]                                                      （12）

式（12）即为粒子在[y]方向上的坐标与动量的不确定关系。这表明：粒子的坐标与动量二者不能同时确定，也可以认为，一个量越确定（即变化范围越小），另一个量不确定程度就会越大（即变化范围越大），即

[Δy↓→ΔPy↑Δy↑→ΔPy↓]                                                     （13）

對比式（6）与式（13）物理量之间的对应关系如表1所示：

通过表2中所示的单缝衍射和不确定关系各个物理量之间的对比可以通过对光的单缝衍射实验特点与规律更好的理解量子力学中的不确定关系，通过在实际的教学过程当中分析也易得，采用对比法的讲解效果明显优越于传统法，如下表3及图4所示。

四、结束语

不确定关系反映了微观粒子运动的基本规律，是微观粒子具有波动性和粒子性两重性的必然体现，也是物理学的重要原理之一，微观粒子除了坐标和动量满足不确定关系外，有些其他的物理量如方位角与动量矩、时间和能量等也都满足不确定性关系。其集中反映了量子力学规律的特点，规定了经典力学轨道概念的适用程度[8]。在经典力学看来，质点都有一定的运动轨道，在任意时刻都有确定的位置和动量，即[Δy=0]，[ΔPy=0];从不确定关系看来，粒子的位置越确定，即[Δy]越小（[Δy→0]），动量的涨落[ΔPy]就会越大（[ΔPy→∞]），反之，动量测得越准确（[ΔPy→0]），位置的测量不确定范围就会越大（[Δy→∞]）。然而，在式（12）的限制下，如果[Δy]与[ΔPy]都很小，此时可以忽略不计，则轨道概念仍可近似成立，形成了由量子力学向经典力学之间的过渡。总之，不确定度关系给我们指出了使用经典粒子概念的一个限度，这个限度用Plank常量[h]来表征，当[h→0]时，量子力学将回到经典力学，或者说量子效应可以忽略[9]。不确定关系的确立，显示并无绝对“客观”，即与探测者完全无关的自然事物，它在很多领域中有其广泛的应用，如在理论前沿、科技、经济、哲学等方面[10]。在大学物理中有关近代物理的教学中，学生是否理解这一基本原理是其能否踏入量子之门的关键。在教学安排上，光的衍射部分在经典物理的教授范围，并且还配有相关的实验教学，是学生先行学到的内容，且容易掌握，这样通过对单缝衍射特点和规律来理解和掌握不确定关系，更符合学生的认知规律、从而达到相应的教学效果。

[ 参 考 文 献 ]

[1] 曾谨言.量子力学教学与创新人才培养[J].物理，2000（7）：436-438.

[2] 宫昊，程荣龙. 量子力学课程教学中的困惑与思考[J].广西物理，2016（2）：42-44.

[3] 张立彬.中外量子力学教材中有关“波函数的统计诠释”论述的区别与思考[J].大学物理，2013（5）：29-33.

[4] 金石琦. 量子调控物理学[M].北京：科学出版社，2015：6.

[5] 肖运龙. 量子测不准原理以及单边信息理论[R].广州：华南理工大学，2017.

[6] 马文蔚. 物理学[M].北京：高等教育出版社，2014：8.

[7] 苏如铿. 量子力学[M].北京：高等教育出版社，2002：12.

[8] 钱伯初. 量子力学[M].北京：高等教育出版社，2006：1.

[9] 曾谨言. 量子力学[M].北京：科学出版社，2013：10.

[10] 袁爱芳，刘迪迪. 浅析量子力学中的不确定性原理[J].大学物理，2011（11）：44-49.

[责任编辑：张 雷]

[收稿时间]2020-05-18

[基金项目]浙江省教育厅一般科研项目（Y201737504）。

[作者简介]张玉强（1977-），男，山东临沂人，武警海警学院副教授，博士，主要从事量子物理研究和物理教学研究工作。