基于决策树算法的热毒宁注射液金银花青蒿醇沉过程质量控制研究

丁 鸿，徐芳芳，杜 慧，张 欣,3，徐 冰，吴 云,3，王振中,3，肖 伟,3*

1.南京中医药大学，江苏 南京 210023

2.江苏康缘药业股份有限公司，江苏 连云港 222001

3.中药制药过程新技术国家重点实验室，江苏 连云港 222001

4.北京中医药大学 中药信息学系，北京 102400

热毒宁注射液是由金银花、青蒿和栀子3 种中药提取精制而成[1-2]，其前提取精制过程包括金银花提取浓缩、青蒿提取浓缩、栀子提取浓缩、金银花青蒿（金青）醇沉、金青萃取、栀子萃取等工序，均在中药数字化提取精制工厂中完成[3]。中药数字化提取工厂配备集散控制系统（distributed control system，DCS）、车间制造执行系统（manufacturing execution system，ΜES）等，可实现对中药前提取设备传感器实时数据以及生产过程数据的抓取。在工业数据的挖掘与分析中，机器学习是常用的方法之一[4]。杜慧等[5]以金银花和青蒿浓缩浸膏醇沉工序为研究对象，采用偏最小二乘法（partial least squares，PLS）进行数据挖掘，PLS 需要对预测变量和目标变量进行降维投影处理[6]，不利于直观解释生产规律，该研究筛选了关键变量但未划分变量的控制范围，不便于生产的实际调控。决策树算法是机器学习中一个树状预测模型，适用于多阶段决策、表查找和最优化等问题，能够直观解释决策过程，目前已成功应用于医疗、广告、交通和金融等多个领域[7-8]。本实验采用决策树及其相关算法对历史数据进行分析，深入挖掘并寻找关键变量的优化控制范围，期望提升热毒宁注射液的质量控制水平。

1 材料

建模数据由江苏康缘药业股份有限公司数字化提取工厂提供，金青中间体批次为170105 至180905共205 批；数据的训练集和测试集的划分应用Python 的Scikit-Learn 工具实现。建模算法均在Salford Predictive Μodeler 8.3（美国Μinitab 公司）实现，单值过程控制图在Μinitab 19（美国Μinitab公司）绘制。

2 方法

2.1 目标变量的确定

金青醇沉工段由金青浸膏分配、金青浸膏醇沉、上清液暂存和上清液回收4 个过程组成。金银花和青蒿的水提浓缩浸膏通过称量罐称定质量后分配至2 个醇沉罐（醇沉罐1 和醇沉罐2），在醇沉过程中，向分配浸膏的2 个醇沉罐中分3 个阶段按不同的体积流量加入一定量的乙醇并不断搅拌，搅拌停止静置一段时间并将醇沉上清液通过真空泵转入浓缩罐，刮板浓缩后得金青醇沉浸膏。金青醇沉工段简图如图1所示，各过程主要参数如表1所示。前期辨识出金青醇沉工段的关键因素为金青醇沉上清液和上清液传料体积、金青总质量、醇沉罐1 及醇沉罐2 金银花浸膏质量[5]。上清液传料体积为上清液暂存罐传送至浓缩罐的上清液体积；醇沉上清液为上清液暂存罐收集的上清液体积；金青浸膏总质量为2 个醇提罐加入金银花和青蒿总质量；醇沉罐1和醇沉罐2 金银花质量为分配至2 个醇沉罐的金银花质量。所筛选的参数均为金青浸膏醇沉过程输入物料及输出物料的质量和体积参数，醇沉过程工艺较复杂，涉及影响因素较多，为进一步挖掘潜在规律，本研究选择金青浸膏醇沉过程为研究目标建立过程模型。

表1 金青醇沉4 个过程的主要参数Table 1 Main parameters of four processes of LA alcohol precipitation

图1 金青醇沉回收工段流程简化图Fig.1 Data map for LA alcohol precipitation process

为消除过程物料质量体积相关性对模型的影响，本研究拟以浸膏醇沉过程收率为目标变量。将金青浸膏醇沉收率和金青醇沉工段收率进行相关性分析，相关图如图2所示，相关系数（r）为0.653。控制浸膏醇沉过程对提高金青醇沉工段的生产效率十分重要。综上，本实验以金青浸膏醇沉收率作为目标变量，建立浸膏醇沉过程模型。

图2 金青浸膏醇沉收率与金青醇沉工段收率相关图Fig.2 Correlation diagram between yield of LA extract alcohol precipitation and yield of LA alcohol precipitation section

2.2 建模数据准备

本实验建模数据主要来源于批记录及数字化提取工厂数据库集成数据。批记录为手动录入，主要为原料药、中间体物料相关数据；数据库收集的数据主要从DCS 系统中收集各个设备传感器实时生产过程中抓取的时序数据，抓取频率为每分钟1 次。中药生产环境复杂，不同时间点内时序参数相关性强，前期对DCS 数据进行数据清洗和特征提取后得到建模特征参数[6]。本实验在建模特征参数中选择30 个醇沉罐传感器数据参数纳入建模数据集，考虑到浸膏质量和加醇体积间存在较强的相关性，本实验将金银花浸膏质量、青蒿浸膏质量和加醇量转化为金青浸膏质量比和加醇料液比。在中药制剂的过程中，中药材的质量差异会传递至处方药味、中间体及成品，直接影响中药制剂批间质量的稳定[9]。为考察药材及金银花浸膏及青蒿浸膏的各生产阶段可能对醇沉过程的影响，收集药材质量参数、药材厂商及药材至浓缩浸膏各过程工序的收率作为预测变量，样本收集时间为2017年1月—2018年9月，共205 批历史数据。以批号关联建模参数，建模参数共49 个，最终得到205×49 的建模数据集，建模变量如表2所示。

表2 金青浸膏醇沉过程49 建模变量Table 2 Fourty-nine modeling variables in LA extract alcohol precipitation process

2.3 建模算法

决策树（decision tree）是一种基本的分类和回归方法，该学习方法主要包括特征选择、决策树生成和修剪，目前决策树学习常用的算法有ID3、C4.5和分类与回归树（classification and regression tree，CART）[10]。当单一决策树学习器不能很好地处理问题时，可尝试集成学习方法（ensemble learning）提高模型预测性能。集成学习通过训练多个学习器并进行组合来解决同一问题[11]。Bagging 算法和Boosting 算法是2 种经典的集成学习算法[12]。本实验采用CART 算法以及随机森林、TreeNet 2 种集成树算法进行建模。

2.3.1 CART CART 模型是应用广泛的决策树算法[13]，它是由特征选择、树的生成及剪枝组成，既可以用于分类，也可以用于回归[10]。相较于ID3，CART 算法选择基尼不纯度作为度量标准，并采用二分递归分割方法划分数据集，最终生成二叉决策树，二叉划分适用更加广泛，也更易处理数值型数据[6]。

2.3.2 随机森林（random forests，RF） RF 是由多个Bagging 算法训练的决策树组合而成[14]，在解决回归问题时，其以多个决策树的平均值为输出结果[12,15]。它是通过利用bootstrap 重抽样方法从原始样本中抽取多个样本，没有抽到的样本被称为带外数据（out-of-bag，OOB）[16]。OOB 误差估计是RF算法的一个无偏估计，可替代数据集的交叉验证，明显降低计算复杂性[12,17]。

2.3.3 TreeNet TreeNet 被称为随机梯度提升（stochastic gradient boosting）[18]。梯度提升是一种实现Boosting 的方法，其主要思想是每次建模都在前一模型损失函数（loss function）梯度下降方向进行[19]。TreeNet 在训练的过程中首先生成1 棵小树并计算该模型的预测残差，之后建立第2 棵树对第1 棵树的残差进行预测，第3 棵树对前2 棵树的残差进行预测。上步骤递归，新产生的小树对前面的模型进行不断修正，最终得到最佳模型。

2.4 数据集划分与训练

数据按3∶1 的比例随机划分为训练集和测试集。通过训练集的数据来训练数据，用测试集来评估模型。在训练模型的过程中需要训练不同模型参数的模型来筛选最佳模型，将保留训练集的一部分来评估各个模型的性能，新的保留集称为验证集。本实验采用10 折交叉验证来评估CART 和TreeNet的训练模型，RF 为OOB 误差估计。本实验以均方根误差（root mean square error，RΜSE）、平均绝对偏差（mean absolute difference，ΜAD）以及决定系数（R2）作为模型评价指标。RΜSE 及ΜAD 越接近0，R2越接近1 表示模型误差越小，性能越好。

n为校正集或验证集的样本数，t∈[1，n]，y为参考值，yi为预测值，为所有样品参考值的平均值

3 结果与分析

3.1 各模型性能评价

基于训练集数据分别建立CART、RF和TreeNet模型，并采用10 折交叉验证来评估不同超参数的CART 和TreeNet 训练模型性能，OOB 误差估计评估RF 模型性能。最终得到各模型最佳的超参数设置如表3所示，最优模型的性能评价指标如表4所示，各模型的预测变量重要性如表5所示。由表5中可知，与CART 算法相比，RF 和TreeNet 2 种集成树算法的验证集和预测集均方根更小，决定系数更大，模型效果更好。说明集成学习算法有效地提高了单一决策树算法模型的性能。

表3 3 种模型的超参数设置Table 3 Hyperparameter setting table of three models

表4 3 种最优模型的性能指标评价Table 4 Performance index evaluation of three models

由表5可知，3 种模型的共同重要变量为X16（罐1 料液比）、X34（罐2 料液比）和X5（金银花提取液浓缩收率）。以这3 个变量建立模型，其模型效果如表6所示。

表5 CART、RF 和TreeNet 模型变量重要性Table 5 Importance chart of predicted table of CART,RF and TreeNet

表6 筛选后3 种模型的性能指标评价Table 6 Performance index evaluation of three models after screening

由变量筛选后模型性能观察比较可知，变量筛选后测试集和预测集的模型误差及R2变化较小，均保持较好的模型性能。说明醇沉罐1 料液比、醇沉罐2 料液比以及金银花提取液浓缩收率为金青浸膏醇沉过程的关键变量。

3.2 关键变量依存性分析

为进一步描述3 个关键变量与目标变量的潜在规律。对TreeNet 模型的3 个关键变量的变量依存度图（partial dependency plots，PDPs）进行分析，单变量依存性散点图如图3所示。

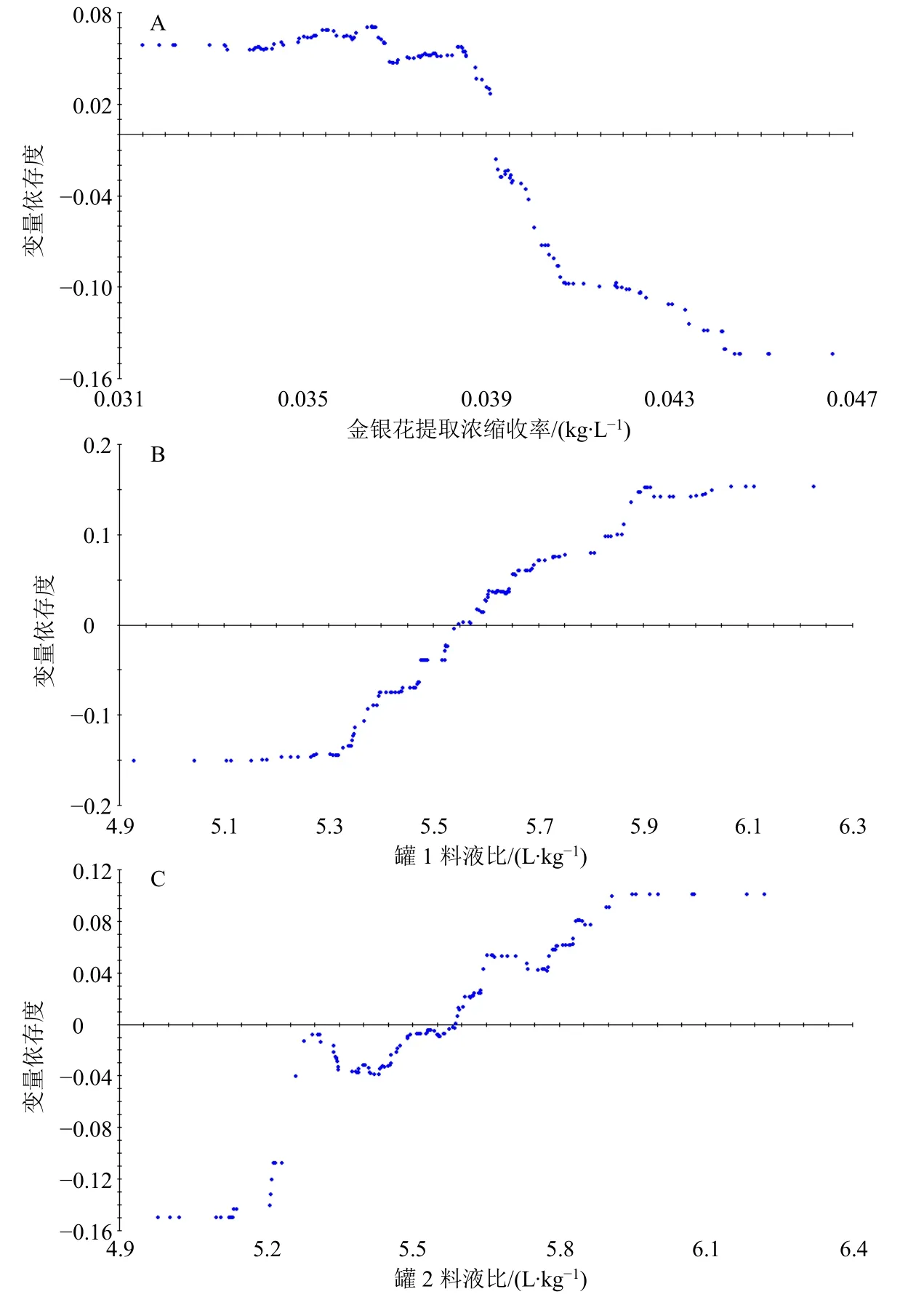
图3 关键变量为金银花提取液浓缩收率 (A)、罐1 料液比 (B) 及罐2 料液比 (C) 单变量依存度散点图Fig.3 PDPs of univariate dependency with key variable were concentration yield of honeysuckle extract liquid (A) and solidliquid ratios in extraction tank 1 (B) and that in tank 2 (C)

通过对3 个关键变量的PDPs 分析，各变量与其部分依存度不是简单的线性关系。变量依存度分析以响应值的正负表示对转化率影响的好坏，将工艺优化问题转化为计算问题。当金银花提取液浓缩收率小于0.039 kg/L 时，目标变量预测响应值为正值。醇沉罐1 和醇沉罐2 料液比的依存度随料液比的不断增加的变化可分为3 个范围：料液比较低，当料液比较小时依存度为负值，较小的料液比将降低目标变量的预测响应值；料液比居中，随着料液比的不断增加依存度也逐渐提高并转为正值；料液比较高，当增加到一定范围时，料液比的增加对目标变量预测响应值的影响不变。将料液比控制在合适区间，在提高金青浸膏醇沉的收率同时可避免加入过量乙醇，降低生产成本。

模型结果中醇沉罐1 的料液比控制范围大约为5.54～5.91 L/kg，醇沉罐2 的范围大约为5.58～5.91 L/kg。对2 罐的范围进行中位数检验，分析2 罐间是否存在差异，以便于确定是否需要分罐控制。结果如表7所示。

表7 不同提取罐料液比中位数Table 7 Median of solid-liquid ratios in different extraction tanks

醇沉罐1 和醇沉罐2 相比，P值＞0.05，总体中位数相等，醇沉罐1 和醇沉罐2 间料液比优化范围无显著差异。综上，醇沉罐1 和醇沉罐2 可统一控制，为控制金青浸膏醇沉过程的收率，需主要对金银花提取液浓缩收率和各罐料液比进行控制。

3.3 关键变量过程控制

上文筛选影响金青浸膏醇沉的关键变量为金银花提取液浓缩收率和料液比，金银花醇沉上清液浓缩收率的影响因素较多，涉及上一工段各工艺参数及设备过程参数，需另外建模研究。本实验主要对料液比的过程控制进行研究。

控制料液比主要控制金银花浸膏、青蒿浸膏和加醇量。通过收集落入优化范围内外的金银花浸膏、青蒿浸膏和加醇量，进行中位数检验分析差异。结果如表8所示。统计分析表明，影响料液比的变化主要是由于金银花浸膏质量和加醇量的波动引起的。企业内部控制标准中要求金银花浸膏浓缩至1.10～1.12 g/cm3（70～80 ℃），并分别对密度为1.10、1.11、1.12 g/cm3的浸膏的出膏量给出不同的控制范围。依存度分析优化范围内的金银花浸膏出膏温度均符合要求，浸膏密度分为1.11、1.12 g/cm3。分别对密度为1.11、1.12 g/cm3的金银花浸膏做控制图，控制图如图4所示。

图4 密度为1.11 g·cm-3 金银花浸膏质量 (A) 与加醇量 (B) 及密度为1.12 g·cm-3 金银花浸膏质量 (C) 与加醇量 (D) 的过程控制图Fig.4 Process control diagram of quality of honeysuckle extract with a density of 1.11 g·cm-3 (A),amount of alcohol (B),quality of honeysuckle extract with a density of 1.12 g·cm-3 (C),and amount of alcohol (D)

表8 不同料液比的相关变量中位数Table 8 Median of related variables for different solidliquid ratios

如控制图所示，通过筛选得到密度为1.11 的金银花浸膏分配控制范围为557.92～639.62 kg，加醇量的控制范围为3.370～3.828 m3；密度为1.12 的金银花浸膏的控制范围为540.4～616.9 kg，加醇量的控制范围为3.317～3.859 m3。综上分析，优化范围内加醇量的差异不大，金银花浸膏质量的波动是影响金青醇沉过程的重要因素。需加强对金银花浸膏质量的监控手段和方法，将金银花浸膏质量控制在稳定的优化范围内控制加醇量，从而控制醇沉过程高效稳定进行。

4 总结与展望

醇沉工序是中药提取精制过程的关键工序之一，在实际生产控制过程中对金青醇沉过程控制的稳定性还有待提高。本实验依托热毒宁提取精制生产大数据，收集金青醇沉过程历史数据，以金青浸膏醇沉上清液收率为目标变量，基于决策树算法进行建模分析，综合3 个模型建模结果，筛选出重要变量为金银花上清液浓缩收率和醇沉罐料液比；通过变量依存度分析，优选批次并作金银花质量及加醇量过程控制图优化控制范围。从热毒宁注射液工业数据中挖掘质量传递规律，有利于该产品质量的追溯与控制，促进制造过程的优化及持续改进[17]。

决策树算法在中药工业大数据的建模应用报道较少，本实验首次尝试应用于热毒宁注射液的醇沉过程，相较于PLS 算法，决策树算法在缺失值处理、变量筛选及优化参数范围的划分等方面更具优势，为热毒宁注射液的数据挖掘和质量控制提供新路径。本实验建模数据为生产历史数据，在后续的工作中，还需结合近红外快速检测技术收集中间体含量数据，多目标决策优选工艺参数控制范围。此外，还需持续收集生产数据，不断优化及验证工艺参数控制范围，提升金青醇沉过程的控制水平。

利益冲突所有作者均声明不存在利益冲突