污水管线渗漏诱发地面下陷数值分析

姬 建，夏嘉诚，张哲铭，张 童，李 圣

(1.河海大学土木与交通学院，江苏 南京 210098； 2.中国电力科学研究院有限公司，北京 100055)

地面下陷是指地面由于地下物质移动、强度降低等因素而发生局部渐进下陷或急剧下沉甚至坍塌的现象[1]。近年来，有关城市地面下陷的事故频发，严重威胁了市政基础设施、道路交通以及路面行人的安全。地面下陷的诱发因素有很多，胡聿涵等[2]对国内路面坍塌案例进行了统计分析，指出有55%的路面塌陷事故均是由管线破损渗漏引起的。Ji等[3-4]在研究地下浅埋管线腐蚀破坏及服役寿命预测问题时指出，管线在服役阶段会受到各种因素的影响，城市地区浅埋管线腐蚀现象严重，导致带病运行。由于我国在早期铺设的给排水管线质量较差，并且管线埋深较浅，经常受到各种类型的荷载及扰动，导致地下埋管发生破损、开裂和渗漏现象，并最终导致地面下陷甚至坍塌。由于地下管线隐蔽性强，破损渗漏发生后水体渗流侵蚀的过程难以观测，因此国内外学者多采用室内试验以及数值模拟的方法针对地下管线渗漏造成地面塌陷问题进行研究。

张成平等[5]利用自行设计的室内试验装置，通过不同工况模拟研究了有压给水管线渗漏水位置以及管内水压力变化对地面塌陷的影响规律，得到了泄漏范围越大将导致地面沉降值及沉降范围越大，渗漏水范围会随着渗漏时间、渗漏点位置、管线水压力的变化而变化等结论；张小玲等[6]利用DEM-CMD耦合数值模型，建立了细观数值模拟的力学模型，定性地描述了有压给水管线发生渗漏时造成地面下陷过程的演化规律，并得到地表塌陷模式在有压给水管线渗漏条件下呈圆锥形变化的结论；王越林等[7]将Fluent中的渗流场导入PFC3D的方式，从细观角度研究了无压地下管线裂缝尺寸和裂缝位置对地面沉降的影响。Cui等[8]利用基于耦合的DEM-LBM计算模型预测了有压给水管线发生破损渗漏时地面可能的下陷范围以及下陷形状。

Karoui等[9]通过室内试验，研究了污水管线开裂造成的地面沉降问题，并指出地下水流向、渗漏点周围的水力梯度和土体强度是导致地面沉降的主要因素；Ali等[10]利用室内模型试验模拟因地下污水管线渗漏引起的地表沉降，试验考虑了土壤类型、水流大小以及渗漏位置对地表沉降的影响，并指出地层土壤类型是造成地表沉降的主要原因，最后建立了回归模型对地面风险水平进行预测。

国内外学者较多关注有压给水管线泄漏对地面道路沉陷的影响。但Zaman等[11]指出，因为具有渗漏量在初期较小导致难以探测、渗漏发展时间较长、渗漏影响范围较大等特点，污水管线发生的小型渗漏可能对地面结构的稳定性危害更大，因此有必要研究污水管线泄漏对地面结构稳定性的影响。另外，李梦姿等[12-13]采用各自改进的双应力状态变量的非饱和土强度模型来模拟非饱和土过渡为饱和土时，因强度降低导致的地面下陷现象，计算结果较为准确，但由于各自改进的模型中存在较多难以准确获得的参数，不利于在实际工程中广泛应用，因此，需要用一种新的形式来反映土体强度随饱和度的变化关系。

本文针对城市污水管线渗漏造成的地面下陷现象，采用数值模拟手段对不同埋深的污水管线渗漏造成的影响进行研究，分析污水管线在破损范围不断扩大的情况下，渗漏水体在地层中的扩散规律以及不同管线埋深对地面稳定性造成的影响。

1 渗流与土体强度衰减耦合模型

1.1 非饱和土强度模型

对于同一种土体，当外界条件相同时，饱和度的改变会引起土体抗剪强度的变化，非饱和土的基质吸力在其中发挥着重要作用。为了较为准确地描述非饱和土的这种性质，Fredlund等[14]提出了非饱和土双应力状态变量抗剪强度公式：

τ=c′+(σ-ua)ftanφ′+(ua-uw)ftanφb

(1)

式中：c′——有效黏聚力；ua——破坏面上的孔隙气压力；(σ-ua)f——破坏面上的净法向应力状态；uw——孔隙水压力；(ua-uw)f——破坏面上的基质吸力；φ′——与净法向应变量相关的内摩擦角；tanφb——抗剪强度与基质吸力之间关系的变化速率。由式(1)可知，非饱和土双应力状态变量抗剪强度公式是对饱和土强度公式的修正，因此式(1)也称修正Mohr-Coulomb公式。图1为Fredlund等[14]提出的非饱和土抗剪强度包络面模型，该包络面为一平面且在纵轴剪应力上的截距为c′，斜率tanφb是一常数。

Gan等[15]指出，对于非饱和土的黏聚力，Mohr-Coulmb破坏包络面和剪应力-基质吸力平面有一相交线，该相交线的方程可表示为

c=c′+(ua-uw)ftanφb

(2)

式中：c——考虑基质吸力影响的黏聚力；c′——当净法向应力与基质吸力均为0时，引申的Mohr-Coulmb破坏包面与剪应力轴的截距。当基质吸力为0时，该截距即为有效黏聚力，即饱和状态时的黏聚力。

将式(2)代入式(1)可将经典的非饱和土强度理论与传统的Mohr-Coulmb强度理论统一起来，得到土体由非饱和状态过渡到饱和状态的土体广义强度公式：

τ=c+(σ-ua)ftanφ′

(3)

1.2 考虑渗流与土体强度衰减的耦合计算模型

利用式(3)来反映土体强度随饱和度升高而衰减的现象。由于ABAQUS在描述土体屈服所采用的Mohr-Coulomb准则在渗流计算时无法反映饱和度变化对土体强度参数产生的影响，进而使土体强度衰减的现象，因此需将土体强度参数衰减模型与理想弹塑性模型相结合来反映饱和土强度衰减现象。

在ABAQUS中实现土体强度随饱和度的升高而衰减，设置土体广义强度模型是通过USDFLD子程序实现的。在研究非饱和土抗剪切强度时，许多强度公式含有基质吸力等难以量测的物理项，使得这些公式不能得到广泛运用。因此，相关学者开展了一系列室内试验来确定土体抗剪强度随含水量(饱和度)变化的经验公式，在实际应用中取得了较为满意的结果[16-18]。蔡瑞卿[18]通过对黏性土进行大量的室内试验得到了土体有效强度参数与含水量w之间的经验公式：

(4)

该经验公式得到的黏聚力和内摩擦角随含水量的变化形式与文献[16-17]形式相似，具有较高的可信度。因此，针对黏性土的一般性质并结合实际工程经验，假设该耦合计算模型中土体孔隙比e为0.7，土颗粒相对密度ds=2.7。根据饱和度Sr与含水量w的转化关系：

(5)

将式(5)代入式(4)得到土体有效强度参数与饱和度之间的经验公式：

(6)

强度参数与饱和度的函数关系如图2所示。

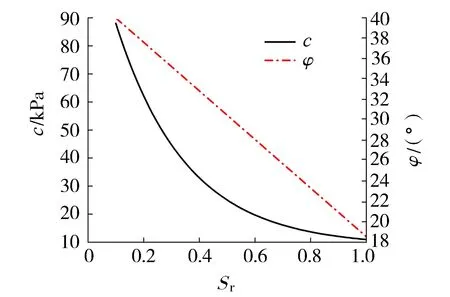
图2 强度参数随饱和度变化关系Fig.2 Relationship between strength parameters and saturation

式(6)的适用范围应与室内试验的情况接近，即土体类型为黏性土，土体饱和度在0.4～1.0之间。在USDFLD子程序中，将每一计算步得到的土体单元饱和度数据赋值给场变量，再将土体强度指标与场变量按式(6)的关系进行设定，即可实现土体强度指标在流固耦合计算过程中更新的效果，达到土体强度随饱和度升高而衰减的目的。

2 数值模拟方法

为了研究污水管线破损渗漏情况下对地面稳定性的影响，采用ABAQUS 6.14软件对因管线渗漏造成土体强度弱化现象进行模拟，结合不同的埋设深度进行数值计算，并探究渗漏水体在地层中的扩散规律以及在土体强度逐渐丧失的条件下地面稳定性情况。

根据污水管线设计规范，管线最小覆土深度应根据外部荷载、管材强度等条件设定，在车行道下管线最小埋深不得小于0.7 m，应根据各地实际情况自行设计。因此，对于模型几何条件的设置，将污水管线的基础埋深设定为1 m，并改变不同管线埋深，参照邹昌喜等[19]的研究，将污水管线直径设为500 mm且保持不变。为了便于计算，将地层简化为均一的非饱和地层，按照平面应变问题进行处理。土体屈服准则采用Mohr-Coulomb准则，由于研究主要针对城市地下排水管线渗漏引发的地面下陷问题，因此管线选择城市地下排水管线多选用的混凝土管线，土体选用城市道路下常见的粉质黏土。模型材料参数见表1，其中内摩擦角和黏聚力均是在饱和度为0.5时根据式(6)得到。

表1 模型材料参数

为了减小边界效应对计算分析区域的影响，将模型尺寸设定为30 m×15 m，将网格设置为四边形单元，对管线周边网格进行加密处理，模型共5 414个节点，5 262个单元。模型采用位移边界条件，模型两侧约束x方向位移，模型底部约束x、y方向位移，模型顶部为自由面。在管线上方10 m范围内设置有20 kPa的均布荷载，用来模拟路面车辆荷载。模型几何尺寸以及网格划分效果如图3所示。

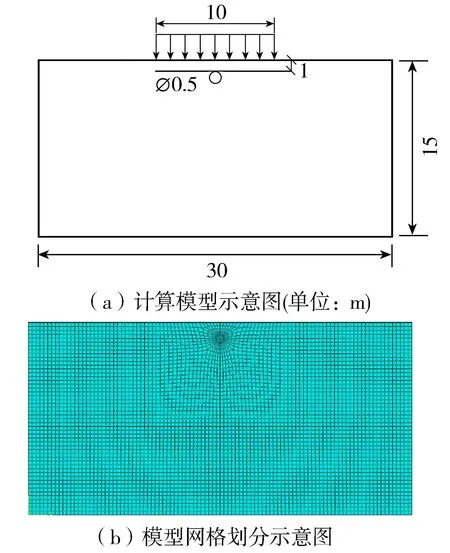
图3 有限元模型示意图Fig.3 Schematic diagram of finite element model

多数学者在研究管线渗漏时，均假定管线的渗漏破损区域不变并以持续的水压向外渗漏，而实际上一旦管线破损口发生渗漏，由于其周围处于非常薄弱的状态[20]，破损口会在短时间内发生扩张现象，导致破损范围扩大。为了模拟管线破损渗漏且破损范围逐渐扩大的效果，根据污水管线设计规范，管径在500～900 mm之间的污水管线，其最大设计充满度为0.7。因此针对本文所采用的管线尺寸，污水管线内水面最高位于管线中心以上100 mm，角度大约为22°，具体如图4所示。

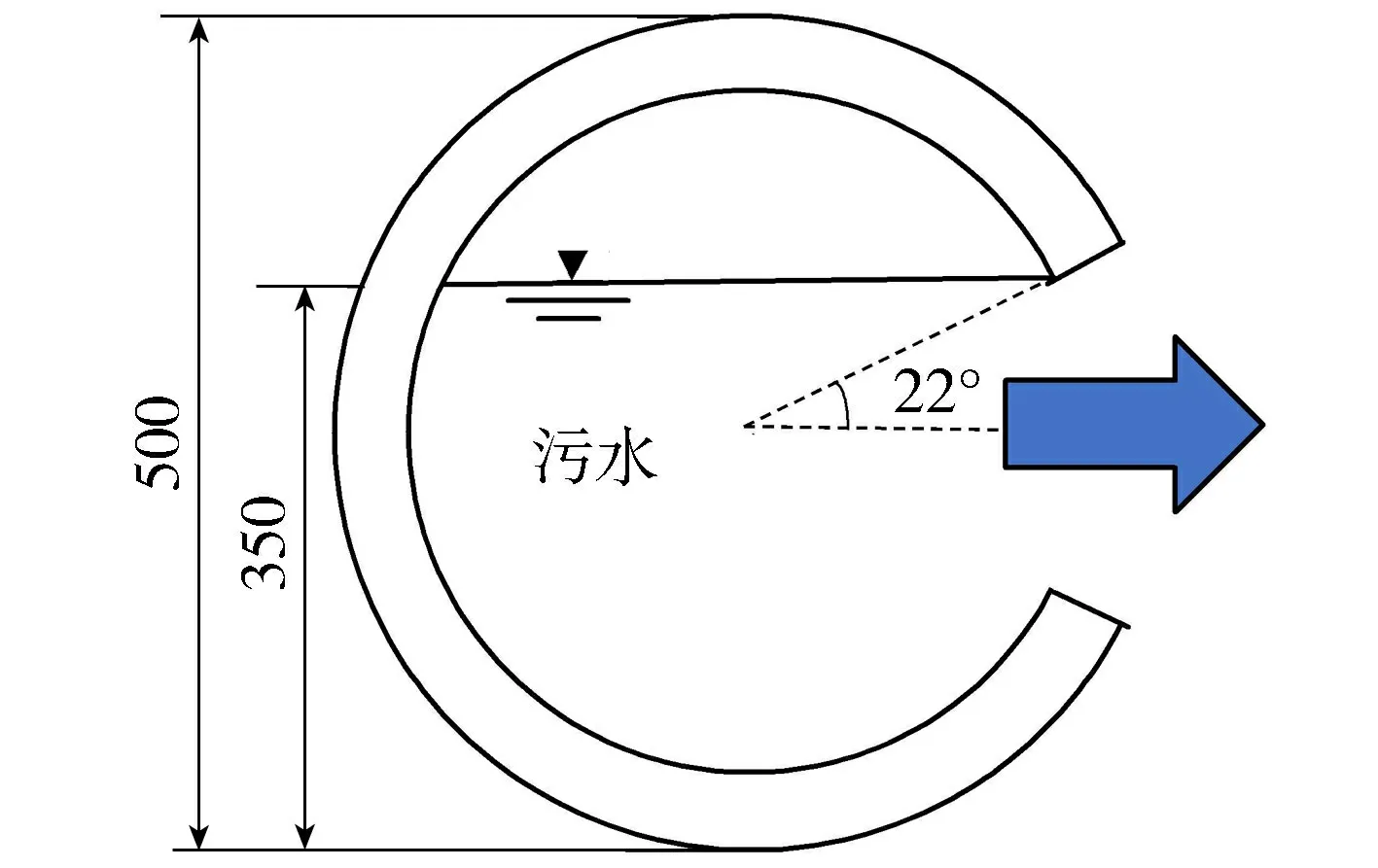
图4 污水管线渗漏示意图(单位：mm)Fig.4 Leakage diagram of sewage pipeline (unit: mm)

采用孔压约束条件模拟管线渗漏。由于污水管线属于低压管线，其内部水压不得超过100 kPa。郑源等[21]指出，孔口渗漏压力与破损范围成正相关，因此将初始孔口渗漏压力设为50 kPa，渗漏位置选择在管线右侧壁中部，渗漏时间为7 d；随后破损范围向上、下各扩展10°，孔口渗漏压力达60 kPa，渗漏时间为7 d；最后破损范围继续向上、下扩展10°，其中上部接近最高设计水位，孔口渗漏压力达到70 kPa，渗漏时间为5 d。

根据蔡瑞卿[18]的研究成果，选择VGM模型作为该类非饱和土的SWCC曲线，同时根据一般路基土体所处的环境，将模型中土体的初始饱和度设定为0.5。

3 结果与分析

3.1 污水管线渗漏条件下土中水体扩散规律

根据不同的渗漏时间观察渗漏水体在地层中的扩散形式，了解渗漏发生后受影响的土体区域，有助于判断污水管线渗漏可能造成的地面下陷范围以及下陷量的大小。图5为当污水管线发生渗漏破坏且破坏范围逐渐扩大时，不同渗漏时间土体饱和度的变化情况。

图5 饱和区域随渗漏时间的发展云图Fig.5 Development of saturated area with leakage time

由图5可知，在污水管线发生渗漏且破损范围逐渐扩大的情况下，污水管线周围土体含水率不断提高，土体饱和区域以渗漏位置为起点向四周持续扩散。在污水管线发生渗漏19 d后，如果没有及时发现并干预，管线上方约10 m范围的地面土体将全部变为饱和土。由于土体从初始状态变为饱和状态时抗剪强度下降明显，很容易导致地面下陷、失稳，对地面的稳定性、地上结构物甚至人民生命财产安全造成影响。

确定地面饱和区范围有助于更好地了解由于污水管线渗漏造成地面沉降的大致影响区域，因此有必要研究地面饱和区的发展过程。图6为埋深1 m时，地面饱和区范围随时间的发展规律。

图6 地面饱和区范围随渗漏时间的发展Fig.6 Development of saturated area in ground surface with leakage time

由图6可知，在渗漏发生的第1天内地面土体处于非饱和状态，并未形成饱和区；渗漏发生的第2天，由于土体内部渗流通道的发展，地面开始出现饱和区，随后饱和区不断扩展；渗漏发生第8天时，地面饱和区突然扩大至5 m，并且随着渗漏时间的推移，饱和区范围逐渐扩大并在第14天时饱和区范围扩展至7 m；在渗漏发生的第15天，饱和区范围再次突变，并在19 d后扩展至10.2 m。从图6可以看出，污水管线渗漏形成的地面饱和区范围随渗漏时间以近似线性方式扩展，随着破损范围的扩大，地面饱和区范围会发生突变，并且相应的扩展速率也将提高，因此考虑管线破损范围的发展是有必要的。

为了探究污水管线埋深与饱和区的关系，研究了管线埋深从1 m变化到5 m时，地面饱和区的发展情况(图7)。从图7可以看出，随着污水管线埋深的增加，地面开始出现饱和区的时间延后。这主要是由于污水管线埋深增加导致渗径增长，渗漏水体到达地面的时间必然增加。当污水管线埋深为2 m时，地面饱和区范围最大，渗漏发生19 d后可达11 m；除埋深为2 m的工况外，地面饱和区范围与污水管线埋深近似呈反比关系，管线埋设越深，地面饱和区范围越小，当埋深为5 m时，渗漏发生19 d后地面饱和区范围仅为1 m埋深对应范围的55%，表明埋设较浅的污水管线渗漏造成的影响范围较大，而埋设较深的污水管线渗漏则较为隐蔽，产生的影响范围较小。

图7 污水管线埋深对地面饱和区发展的影响Fig.7 Influence of buried depth of pipelines on development of saturation area of ground surface

3.2 污水管线渗漏对地面稳定性的影响

为了反映在路面荷载作用下，土体由于污水管线渗漏从非饱和状态过渡为饱和状态强度降低进而导致地面逐渐下陷的现象，利用FORTAN语言编写了USDFLD子程序，将土体强度参数与饱和度的函数关系在ABAQUS有限元模型中实现。

图8为污水管线埋深为1 m时地表沉降量与渗漏时间的关系。从图8可以看出，随着渗漏时间的发展，虽然路面荷载保持不变，但由于污水管线周围土体逐渐从非饱和状态过渡为饱和状态，土体强度降低，使得地面随着渗漏时间的推移而逐渐下陷；并且由于污水管线渗漏位置的不对称，造成地面沉降趋势的不对称，这可能比均匀的地面沉降产生更加严重的后果。表2为污水管线正上方土体因污水渗漏导致地表湿陷的情况。

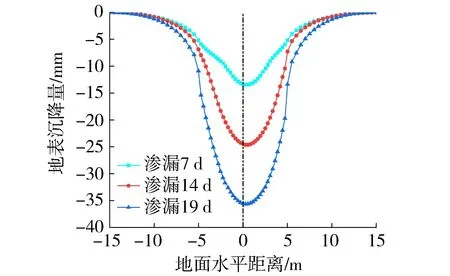
图8 污水管线埋深为1 m时地表沉降量与 渗漏时间的关系Fig.8 Relationship between surface subsidence and leakage time with buried depth of 1 m

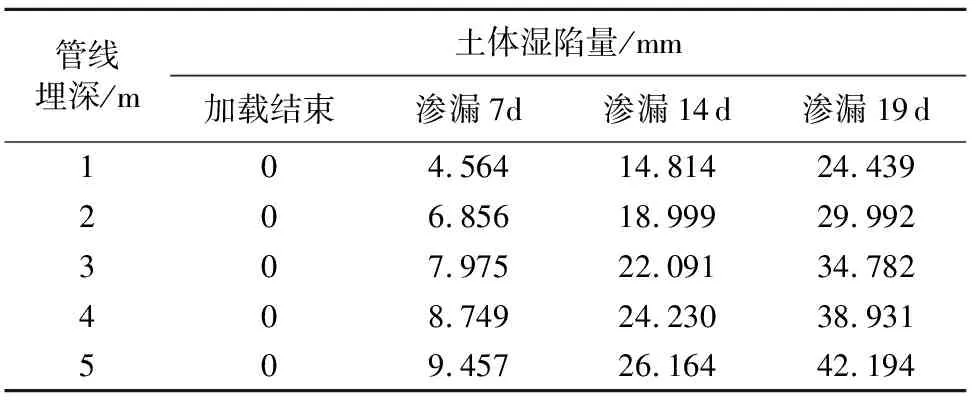
表2 污水管线正上方土体湿陷量

从表2可以看出，随着渗漏时间增长，渗漏量不断加大，土体饱和度逐渐提升，土体强度不断降低，加剧了地面的下陷程度；虽然最后渗漏阶段只持续了5 d，但由于破损范围的扩大，其产生的下陷速度明显高于前两阶段，造成了显著的地面下陷，这也说明考虑破损范围随渗漏的发展不断扩大是很有必要的。同时，随着污水管线埋深的增加，管线渗漏造成的地面下陷量不断增大，地面稳定性不断降低。这主要是因为管线埋深越大，渗漏水体向上渗流至地表的距离越远，地面下受影响的土体范围越大，因此地表将产生更大的下陷量，更容易发生失稳现象。

结合国内外地铁施工量测数据管理标准，将地表最大湿陷量为30 mm设定为地表失稳的判据，图9为不同埋深的污水管线发生渗漏时，地表安全系数随渗漏时间的变化。

图9 地表安全系数与渗漏时间的关系Fig.9 Relationship between safety factor of ground surface and leakage time

由图9可知，不同污水管线埋深对应的地表安全系数在渗漏发生的前10 d内变化明显，埋深越浅其安全系数越大。埋深为1 m的污水管线对应的地表安全系数明显高于其他埋深条件下的地表安全系数，并且在研究时间内，地表安全系数均大于1，地面结构相对比较稳定。埋深为2～5 m的污水管线在渗漏后期所对应的地表安全系数差别不大，在渗漏发生的第15～19 d内，不同埋深管线对应的地表安全系数相继小于1，按照选择的失稳判据可认为地表已经失稳，并且埋深越浅地表发生失稳的时间越晚。同时，这也反映出污水管线等小压力管线的渗漏存在隐蔽性、渗漏从发生到失效的周期较长、失效时造成的影响较大等特点。

4 结 论

a.污水管线发生渗漏时，由于其初始规模较小，形成的影响范围比较有限。随着破损范围的扩大以及时间的增长，管线渗漏将在地面以下形成大面积饱和区，降低土体强度，影响地面稳定性。

b.污水管线埋深不同，渗漏造成的影响范围也不尽相同：管线埋深5 m时，渗漏造成的影响范围最小；管线埋深2 m时，渗漏造成的影响范围最大。

c.将地面最大沉降量为30 mm作为地面失稳判据，比较不同埋深污水管线对应的地面稳定性随渗漏时间的变化关系。污水管线埋深为1 m时，地面始终保持稳定，埋深为2～5 m时，地面稳定性在渗漏后期差别较小，在渗漏发生15～19 d内，各埋设深度的污水管线对应的地表安全系数由深至浅依次小于1，地面发生失稳现象。

综上所述，污水管线发生渗漏与给水管线发生渗漏对地下土体饱和区的发展、地面稳定性的影响是有很大差别的。当地下污水管线的埋深不同时，周边地面受到的影响范围、地面稳定性随渗漏时间的变化情况亦有差别。这为今后地面塌陷检测和预防工作提供了很好的思路，除了关注给水管线的渗漏外，还应加强对污水管线的检查力度。通过对地面饱和度等参数进行反分析，可对地面失稳问题进行提前预判，为城市道路安全管理提供参考。