初中数学探究式课堂教学的几种体现模式
2021-10-11陈先锋
陈先锋
摘 要:所谓探究性教学是以探究为主的教学,是指教学过程在教师的启发诱导下,以学生独立学习和讨论为前提,以现行教材为基本探究内容,现行初中数学教材特别增加了探究性活动内容,以学生周围世界和生活实际为参照对象,为学生提供充分自由表达。质疑、探究、讨论问题的机会,让学生通过个人、小组、集体等多种解难释疑尝试活动,将自己所学知识应用于解决问题的一种教学形式。通过探究获取直接经验和体验,能养成科学精神和科学态度,能掌握基本的科学方法,提高运用知识发现问题、分析问题和解决问题的能力。探究性课堂教学是在教师指导下,学生运用探究方法进行学习,主动获取知识,发展能力的课堂活动。教学程序是:从问题出发,通过探究、猜想、归纳、证明,从而使问题得到解决。
关键词:探究猜想;归纳;证明;灵活运用公式
下面就谈谈数学教学中,常见的概念课、定理课、公式课、习题课四种不同类型课堂教学的体现形式。
1.数学概念课的探究性教学模式:情景→探究→形成概念→深化→应用
在概念教学中,关键在于要有好的教学方法,在教法改革中充分运用知识迁移的原理,突出基本概念的教学,加强知识间的内在联系,适时进行渗透,使前面的学习为顺利地学习后面的知识打好基础,把新旧知识联系起来,使学生形成一个最佳的认知结构。 例如,对九年级第二十二章二次函数中的“二次函数”概念教学
①创设问题情景,增加感性体验
出示问题:(1)如果改变正方形的棱长为x,那么正方体的表面积y会随之变化,y和x之间有什么关系呢?
(2)n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数与球队数n有什么关系?
问题(1)尝试由学生解决,问题由学生完成问题;问题(2)师生共同完成,利用多媒体有序揭示意图,学生小组讨论
②形成新概念
通过观察实际问题引出的函数定义二次函数,
③深化概念
讨论:(1)二次项系数为什么不等于0?
(2)一次项系数,常数项是否也有限制?
④应用概念
设计一些开放性的题目,培养学生思维的发散性。比如,让一些同學写几个函数,其他同学来判断是不是二次函数。
⑤反思概念(略)
通过对一系列问题的讨论、探讨,将概念纳入到学生已有的知识结构中去,不仅使学生有效地突破难点,准确、全面地理解概念,而且学习了科学抽象、概括等思维方法。
2.数学定理课的探究性的教学模式:观察→猜想→证明→应用
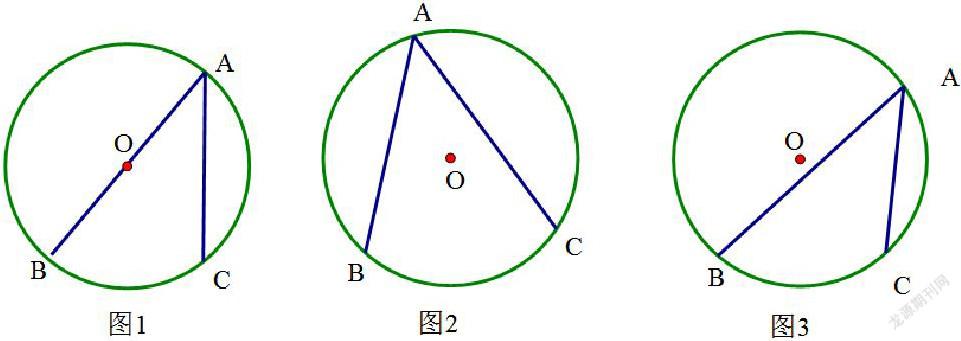
数学定理在初中教材中经常出现,定理课堂教学的形式多种多样,进行探究性课堂教学有助于学生掌握教材中重点、难点,比如:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
①动手探究、观察问题
让学生动手任意画⊙O和⊙O的一个圆周角∠BAC
问题1:当AB为直径时,大家观察∠BAC和∠BOC有什么关系?
问题2:改变∠BAC的大小,当O在角的内部时,大家观察∠BAC和∠BOC有什么关系?
问题3:改变∠BAC的大小,当O在角的外部时大家观察∠BAC和∠BOC有什么关系?
②归纳、猜想、证明定理
通过学生动手观察,小组交流讨论、归纳、猜想实验得出来的结论,让学生口答,并用命题的形式表达出来,然后让学生证明猜想。
③正确理解和应用定理
④深化和拓宽定理的应用
3.数学公式课的探究性教学模式:猜想→实验→证明→运用
公式是一种特殊形式的数学命题,利用探究性教学能呈现公式的由来,指导学生根据公式的外形特点进行记忆并应用。
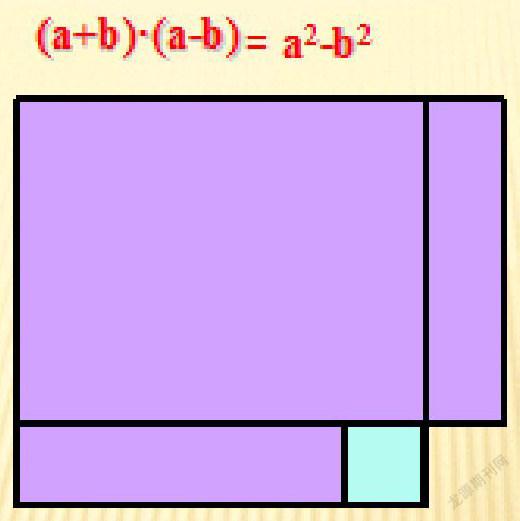
例如“平方差公式”:
①观察、猜想问题,学生小组讨论交流,归纳、猜想,得出结论
计算下列多项式的积.
②实验验证(可以用右图证明)
③数学证明(用多项式的乘法证明)
④应用公式并深化、灵活运用公式。
拓展延伸 利用平方差公式计算:
(1)1992×2008 (2)996×1004
(3)(a+b-c)(a-b+c) (4)(a-2b+3)(a-2b-3)
通过学生自己的观察、思考、比较、猜想、构造及证明,发现了规律,使学生体会到发现和解决问题的重要的方法,尝到了探索成功的喜悦。
4.数学习题课的探究性教学模式:尝试→交流→拓展反思
数学教学中,习题课是巩固课堂知识、查漏补缺、学会解题、发展思维的一种重要课型。习题课是新知课之后,教师有目的、有计划地指导学生运用已学过的知识解决一系列问题的教学活动。因此教师在习题教学时为学生提供自己探究的时空,尽可能放手让学生“动”起来,才能让学生“活”起来,有效的办法是:变“先讲后练”为“不讲先试”。
比如:求证:顺次连结四边形,四条边的中点所得的四边形是平行四边形
①独立尝试
(1)对原题作如下处理:“我们来共同探索一个十分有趣的问题,请大家在草稿本上画一个一般四边形,分别取四边中点,再顺次连结这四个点,请观察,得到的四边形有什么特点?由此会发现一个什么样的结论呢?你能证明你发现的结论成立吗?比赛一下,看谁又快又好?”
(2)学生迫不及待地画图、观察、独立探究,教师巡视,发现学生都能正确地画出图形,并准确判断出是平行四边形,而且有相当部分还完成证明。
②合作交流
由于独立尝试,探究效果好,在小组暂短交流后,就开始全班讨论刚才两位的解答,一位是连结两对角线,用平行四边形定义进行判定:另一位是只连一条对角线,用“一组对边平行且相等”来证,还有同学连两对角线,用“两组对边分别相等”证,在及时肯定他们的同时,留下少许时间让学生讨论、深化,也为中差生提供一个再学习、再消化的时空。
③拓展反思
(1)引导学生及时总结本题蕴含重要知识:三角形中位线性质、平行四边形判定;挖掘解题思想:四边形问题常转化为三角形问题解;提炼解题规律:遇到中点,考虑中位线。
(2)在学生自主探索,并有成功愉悦之时,顺势引导拓展:将“一般四边形”分别改为矩形、菱形,结论有什么变化?为什么?让学生画图→观察→探求后,推出三组问题:
①顺次连结平行四边形、等腰梯形、正方形各边中点,得到四边形分别是________、 ________、 _________;
②当一般四边形两对角线分别满足什么条件,顺次连结各边中点所得四边形是矩形?菱形?正方形?会是梯形吗?为什么?;
③一般四边形的对边中点的连线段有什么特点?平行四边形、矩形、菱形、正方形、等腰梯形呢?为什么?
总之,在课堂教学中,运用探究式教学方法极大的体现了探究的优势和重要作用,激发了他们的学习主动性,促进他们的思维活动,开发了他们的智力,不断为学生创设一个实践、探索、发现、创新的宽松、平等的教学环境,从而使学生在教师的引导、帮助下不断获得成功。
参考文献:
[1]王立贺.活用公式,提升数学课堂教学效率[J].中学教学参考,2015(32):22.
[2]姚婷.授人以渔重思考 循循诱之兴味长——以“函数y=Asin(ωx+φ)的图象”教学为例[J].中学数学月刊,2021(05):20-22.
