面向满应力准则的非线性连续结构截面尺寸优化设计理论与分析

吴 山，何浩祥，周钰婧

（北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124）

结构优化设计是指在给定的约束条件下，按某种优化目标（如重量最轻、成本最低、刚度最大等）获得最优方案的设计方法。根据设计变量的类型，工程结构优化可以分为不同的层次[1]:①尺寸优化，在给定结构类型、材料、布局和几何尺寸的情况下，确定各构件的最优截面尺寸，从而实现结构优化目标，是难度较低、应用最广泛的优化方式[2]；②形状优化，在限定物理参数范围的前提下，将构件的截面形状、节点的空间位置以及连续体的形状等作为设计变量，实现设计区域几何形状的改变，从而优化结构力学性能；③拓扑优化，以材料在设计域内的空间分布作为设计变量，使结构在指定条件下满足性能需求或优化准则。结构优化求解的方法大致包括准则法、数学规划法及智能算法等。准则法是从工程需求出发提出结构优化应满足的力学准则（如满应力准则、刚度准则和能量准则等）并迭代求解的方法，是最基本的优化求解方法。

大量研究表明:各层次结构优化的重要性是没有绝对的高低之分的，应根据工程需求、优化目标、优化准则和计算效率从各层次开展协同研究才能真正实现结构优化设计。近年来，关于连续体拓扑优化的研究比较深入和丰富，并取得了一定应用。但对于实际结构而言，区域边界需要保持光滑的连续性条件，优化的形状边界也需具有足够的可制造性，而拓扑优化过于关注材料分布却并未充分考虑实际条件的限定，加之考虑的荷载工况较单调，故其工程可行性偏弱。因此，基于工程结构的力学特征、普遍需求和优化准则，探究连续体的截面及形状优化的理论形式和力学解析解具有重要的理论和工程价值。

此外，在诸多优化准则中，满应力设计准则是最受关注的，其主要思想是在指定受力模式下使结构的每个构件或部分均达到承载力极限或设计容许值，从而使构件的强度得到充分利用[3]。在传统的结构截面尺寸和形状优化研究中，应优先考虑满足满应力设计准则，以避免出现因应力集中导致的局部变形过大或薄弱层破坏。在目前的研究中，通常采用容许应力法或弹性状态假定认为结构始终处于弹性状态而进行优化设计，在此条件下满应力设计准则等效为等强度准则或等应力准则。关于满足等应力准则的构件或简单结构的优化设计研究取得了大量成果。例如，在简单荷载下的矩形截面悬臂梁和简支梁的等应力优化已经较成熟，基于多种拓扑演化策略的平面框架、桁架或简单塔架的等应力优化也取得较令人满意的效果[4]。

需要指出的是，由于工程结构通常会承受地震、风荷载和其他随机荷载的作用，且当激励幅值较大时结构的材料很可能进入弹塑性状态并产生性能退变和较大变形，因此这些作用成为满足结构设计需求的决定性荷载模式，相比简单荷载情况，其优化设计研究更有理论意义。此外，若结构在接近临界破坏弹塑性应力时也较均匀，其各处的损伤也将较接近，因此面向满应力准则的结构优化结果也可为面向损伤的结构抗振设计提供初始优化结果，具有良好的工程意义。然而，目前在力学分析和优化领域，为了简化分析通常将材料本构假定为线性形式，不考虑刚度退化等非线性特性，即并没有真正实现满应力优化设计。因此，对复杂剧烈荷载下的非线性结构满应力优化设计是十分必要的。

综上所述，面向实际荷载及材料特性的工程结构优化设计尚主要存在以下不足:①等应力和等强度设计理念通常被用于简单荷载下的构件优化层面，对复杂荷载下的结构整体优化设计的探究和应用不够深入和全面；②缺乏基于满应力理念的连续悬臂梁结构最优截面尺寸分布的力学机理研究，从而无法为复杂荷载下结构优化设计提供坚实准确的精细化解析方法和公式；③缺乏对材料非线性结构的满应力设计研究，不能满足实际工程结构的弹塑性损伤设计需求和实用性需求。

有鉴于此，本文将诸如连续塔式结构和高层建筑结构等工程结构简化为非线性连续变截面悬臂杆结构，通过构建不同的弯矩表达形式来求得最优截面尺寸解析解，采用通过试验数据拟合获得的二次多项式表征材料非线性本构，分别对圆形、矩形、圆环形和箱形截面悬臂杆在均布荷载、倒三角荷载和与惯性力相关荷载作用下的最优截面尺寸分布公式进行推导求解，得到完全解析解及最优刚度分布解析表达，之后通过有限元分析对以上理论方法和结果进行了充分验证。

必须指出的是，由于实际高层建筑结构构件种类繁多，结构形式复杂，仅从力学优化角度难以获得最优抗侧刚度分布解析解，需要迭代算法对其进行深度优化设计，故本文基于力学理论对简化模型进行理论分析，得到了最优截面尺寸分布和最优抗侧刚度分布解析解，该结果主要可用于对诸如塔式结构等连续悬臂结构的优化设计，同时可为工程结构优化设计提供初始优化解，提高优化效率。

1 不同荷载形式下非线性结构最优截面尺寸分布解析

1.1 结构截面形式、荷载分布模式与材料本构

工程结构在外部激励下发生的位移和损伤通常与结构的刚度分布和质量分布等因素密切相关。经过合理设计的结构刚度通常是沿高度方向连续变化的。连续体等应力优化理论主要适用于水塔、烟囱等构筑物和塔式结构，对于高层和超高层建筑，其楼板约束作用影响较小，其结构在水平荷载下以弯曲变形为主，因此也基本适用[5]。根据高层建筑物或构筑物不同的结构形式和工程需求，等效悬臂杆截面形式可包括圆环形、圆形、箱形和矩形等，其中圆形和矩形截面的最优尺寸分布公式可以由圆环形和箱形截面的公式表示，因此本文主要对圆环形和箱形截面的情况进行解析。在最优截面尺寸分布的基础上，提出最优剪切刚度和弯曲刚度分布，对实际工程设计和规范修订提供参考。

工程结构在不同荷载形式下的最优截面尺寸分布和最优刚度分布是不同的。风荷载和地震作用是使建筑结构发生破坏或损伤的常见不利作用。钟振宇等[6]考虑风重耦合效应，推导了沿高度方向的等效静力风荷载分布，结果表明等效静力风荷载的分布形式非常接近倒三角形；当仅考虑第一振型时，地震作用可以等效为倒三角水平荷载；当考虑全部振型时，可将地震作用简化为均布荷载或与惯性力相关荷载[7]。为了全面考虑风荷载和地震作用，本文考虑均布荷载、倒三角荷载和与惯性力相关荷载三种水平荷载形式。

以满应力为目标的优化设计不仅要求结构在弹性阶段实现等应力，更重要的是结构在塑性状态下的应力相等或相近。目前相关领域的研究为了计算简便，材料本构多假定为线性形式，不考虑刚度退化等非线性力学特性，实际工程多为钢-混凝土结构或钢结构，采用线性材料的研究往往难以应用于实际。为了确保研究在工程中的适用性和可行性，悬臂杆采用均质非线性材料。

1.2 优化问题描述

在地震动和风荷载作用下，对于高层建筑结构，在各层应力水平不超过限值的情况下，希望其应力沿结构高度方向的分布尽量均匀。通过对结构截面尺寸优化设计，以达到上述优化目标。该优化问题可以表述为

式中:Si为结构第i层截面尺寸；σi为结构第i层的应力值；[σ]为结构应力允许值；n为结构层数；t为时间；T为外荷载持时。

1.3 圆环形变截面悬臂杆最优截面尺寸分布

1.3.1 均布荷载下悬臂杆最优截面尺寸分布

大量试验结果表明结构中的钢筋混凝土可以等效为一种拉压同性的复合材料[8]，其应力-应变关系可以通过非线性函数表征。设该材料本构关系为

式中，σ和ε为材料受压产生的应力和应变。受压应力-应变全曲线方程可采用Hognestad建议的混凝土多项式表达式，其对钢筋混凝土等复合材料也具有较好的通用性。假定等效复合材料为各向同性，即受拉和受压时有相同的应力-应变全曲线，有

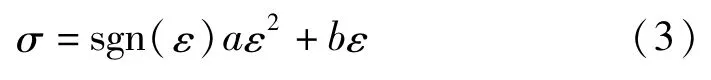
式中，a和b为待定系数。该表达式代表的材料应力-应变全曲线包括上升段和下降段，是材料真实力学性能的全面宏观反应。

首先对均布荷载作用下圆环形变截面梁的最优截面尺寸分布进行求解，将结构等效为悬臂杆，杆件采用均质非线性材料，受压应力-应变全曲线由式（3）表示。计算模型如图1所示，取悬臂杆轴线为x轴，横截面对称轴为y轴，中性轴为z轴。

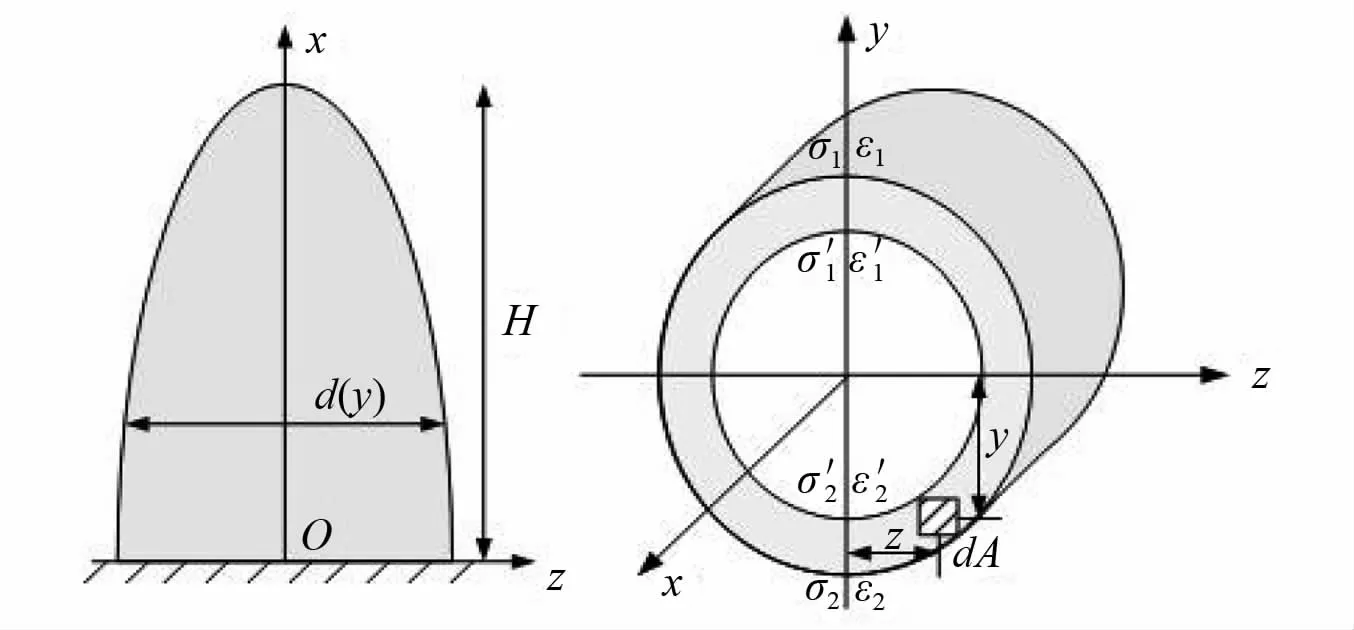
图1 力学模型示意图Fig.1 Mechanical model

首先，通过任意截面下由外荷载形成的弯矩与由梁截面尺寸与弯曲应变表示的弯矩相等的原则，建立弯矩平衡方程。以此原则优化后的悬臂杆结构在水平荷载作用下沿高度方向弯曲应变相等，因结构产生的应变以弯曲应变为主，故近似得Mises应变也是相等的，后文有限元验证提取了结构的Mises应变，对该方法的有效性进行了验证。相应的弯矩平衡方程为[9-10]

式中:M1为由梁截面尺寸与应变表示的弯矩公式；M2（x）为由外荷载表示的弯矩公式。对M1和M2（x）分别进行推导。

悬臂杆结构在小变形时，服从平面变形假定

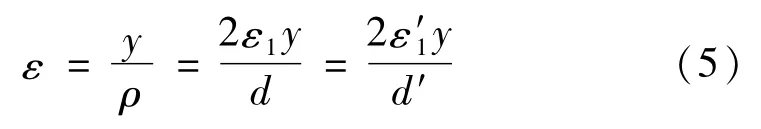
式中:y为纵轴坐标；ρ为曲率半径；d为圆形横截面外直径；d′为内直径；设 σ1，σ2，ε1，ε2和 σ′1，σ′2，ε′1，ε′2分别为横截面内外壁距离中性轴最远两处的应力和应变，即截面中外壁和内壁的最大应力和应变，则横截面弯矩可写成

式中，A为截面微面积。由式（5）及材料拉压性质对称[11]可知，式（6） 可写为

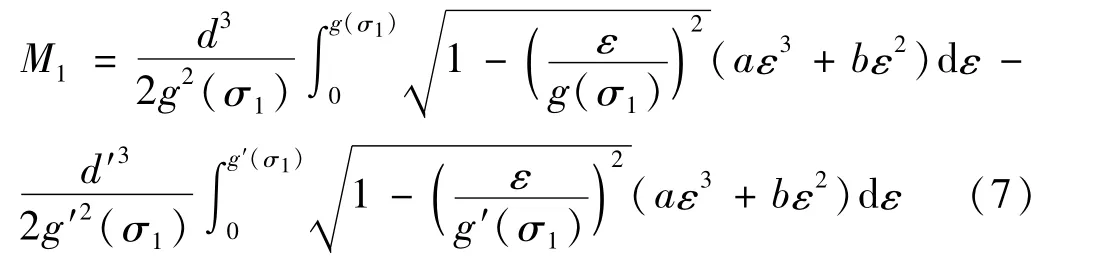
对ε进行换元，设

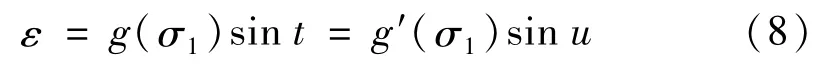
则式（7）可写为

设

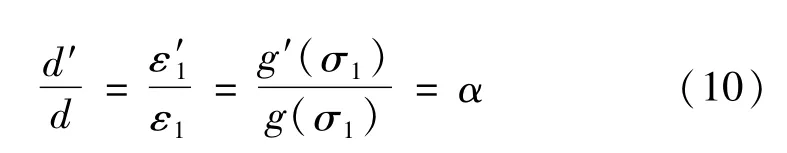
当α=0时，截面为圆形。对式（9）和式（10）整理可得

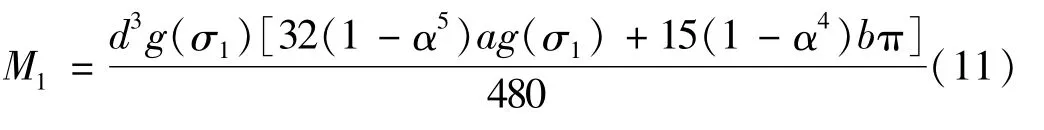
当悬臂杆结构承受水平荷载作用时，在任意高度x处由均布荷载q引起的弯矩M2（x）为[12]

式中，H为结构总高度。将式（11）、式（12） 代入式（4）

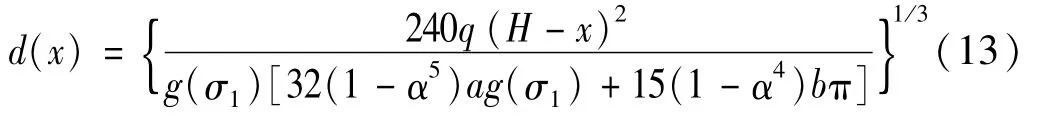
式（13）为圆环形截面悬臂杆结构在均布荷载作用下最优截面尺寸分布解析解，截面尺寸满足式（13）的悬臂杆结构在均布荷载作用下，各截面内最大应力和应变相等。

1.3.2 倒三角荷载下悬臂杆最优截面尺寸分布

倒三角荷载顶部的荷载集度为qmax，底部为0，当作用于悬臂杆结构时，荷载产生的弯矩为[13]

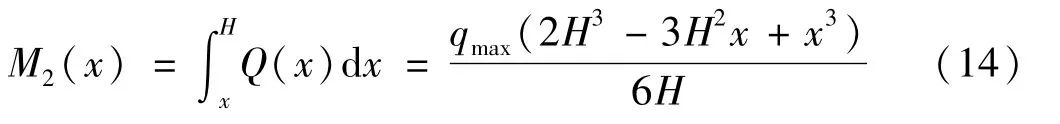
圆环形截面悬臂杆截面内弯矩为式（11），再通过与式（14）相等建立弯矩平衡方程，可以解得最优截面直径分布为

1.3.3 与惯性力相关荷载下悬臂杆最优截面尺寸分布

当圆环形截面变截面悬臂杆结构承受与惯性力相关荷载时，荷载集度可表示为

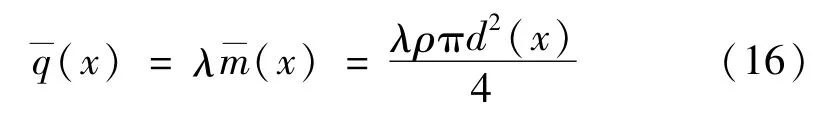
式中:ρ为等效面密度；λ为质量相关系数，用来控制荷载幅值。由于与惯性力相关荷载集度与截面面积有关，而截面尺寸尚且未知，为了求解荷载作用产生的弯矩，进行如下假设

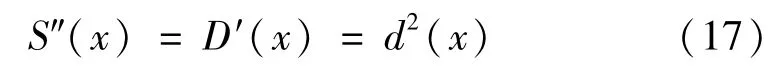
结构任一高度x截面内由于与惯性力相关荷载作用产生的弯矩可以表示为

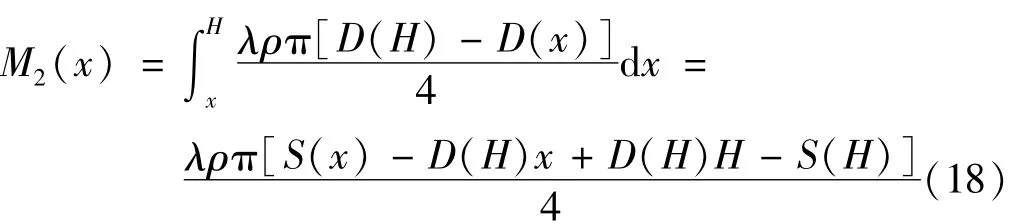
圆环形截面内的弯矩可以表示为（11），与式（18）相等，可得

易知式（19） 为y″=f（x，y） 型高阶微分方程，属不可解类型，故考虑采用假设截面尺寸函数的方法进行求解。

由文献[14]可知，悬臂杆截面形式按照下式分布有利于实现在与惯性相关荷载作用下的等位移原则，其高度分布函数为

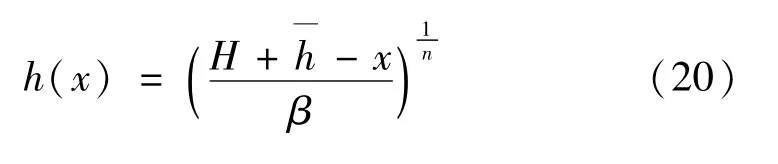
图2 与惯性力相关荷载下的悬臂杆模型Fig.2 Cantilever bar model under inertial force-related load

圆环形截面悬臂杆在与惯性力相关荷载的作用下，任意高度x截面内的弯矩为

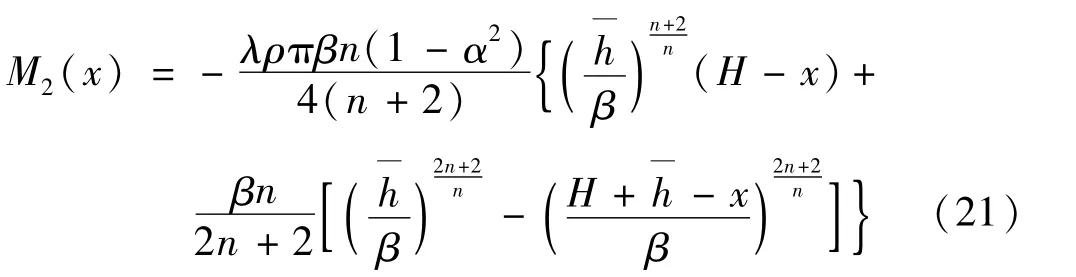
圆环形截面的弯矩可以表示为

令式（22） 与式（21） 相等，得

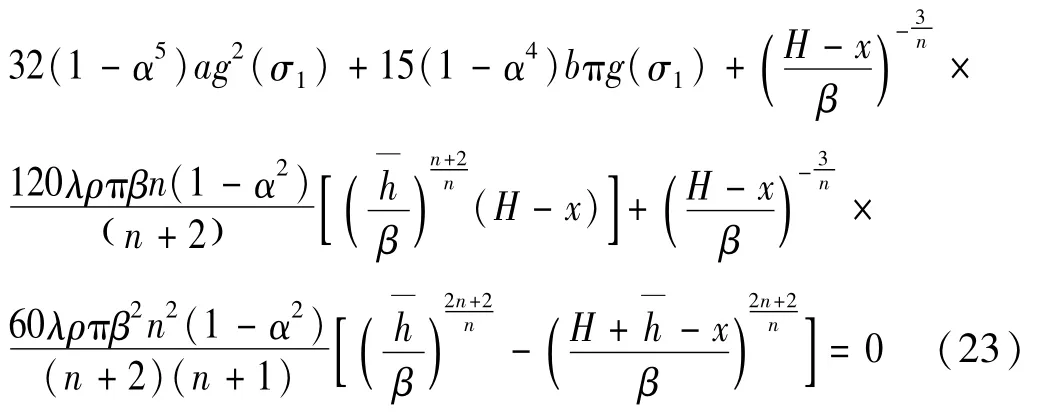
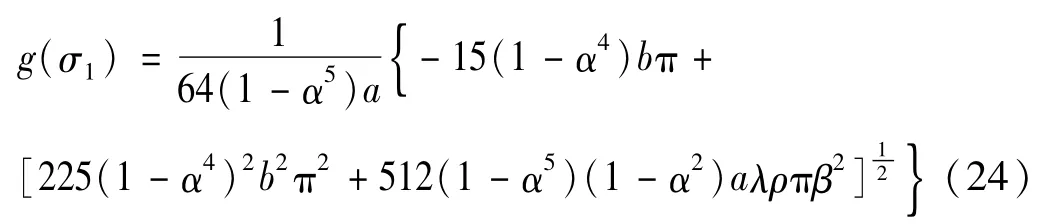
因此，圆环形截面悬臂杆在与惯性力相关荷载作用下最优截面直径分布为

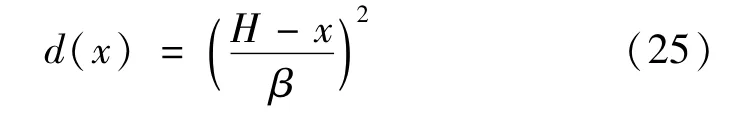
圆环形截面悬臂杆截面尺寸按照式（25）分布，可以实现与惯性力相关荷载作用下的等应力原则。

1.4 箱形变截面悬臂杆最优截面尺寸分布

箱形最优截面尺寸分布和圆环形截面采用相同的原理，过程不再详细描述。箱形外截面宽度B保持不变，对外截面高度h进行优化，设h（x）为截面高度随结构高度变化的函数并求解析解，且有

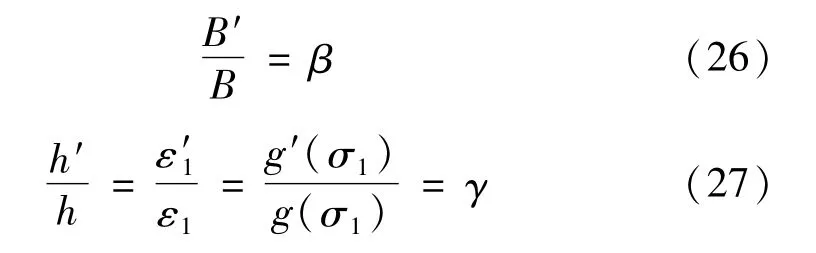
式中:B′为箱形内截面宽度；h′为箱形内截面高度。

均布荷载下箱形截面结构最优截面尺寸分布函数为

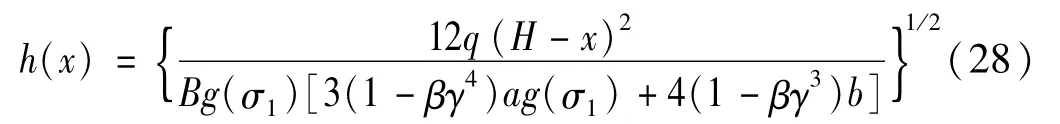
倒三角荷载下，箱形截面结构最优截面尺寸分布函数为

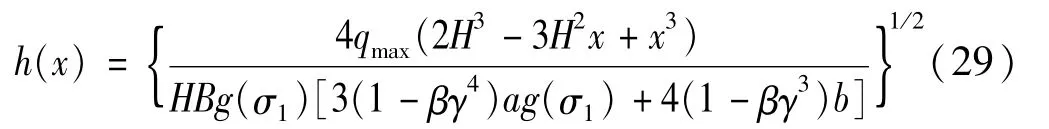
与惯性力相关荷载作用下，箱形截面结构最优截面尺寸分布为

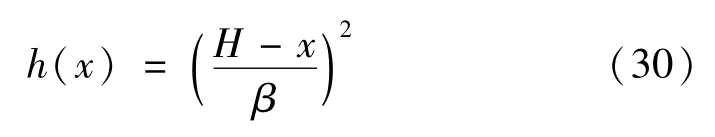
2 基于有限元的验证分析

2.1 非线性材料本构

为了验证本文所建立的理论方法和解析结果的正确性，需确定具体的材料非线性本构模型取值并进行弹塑性有限元分析。对于式（3）中的非线性材料本构参数，可根据试验数据进行拟合确定。本文选择文献[15]中大尺寸钢筋混凝土轴心受压试验的数据进行参数确定。试验中S30-400试件长1 800 mm，正方形截面尺寸400 mm×400 mm，长细比4.5，混凝土强度设计等级为C30，实测棱柱体抗压强度22.3 MPa，纵筋采用HRB335钢筋，实测屈服强度408 MPa，纵筋等效配筋率2.51%，加载制度为拟静力加载，对S30-400试件的应力-应变曲线进行二次多项式拟合，从而确定式（3）中的待定系数a和b，拟合效果如图3所示。式（3）拟合结果为

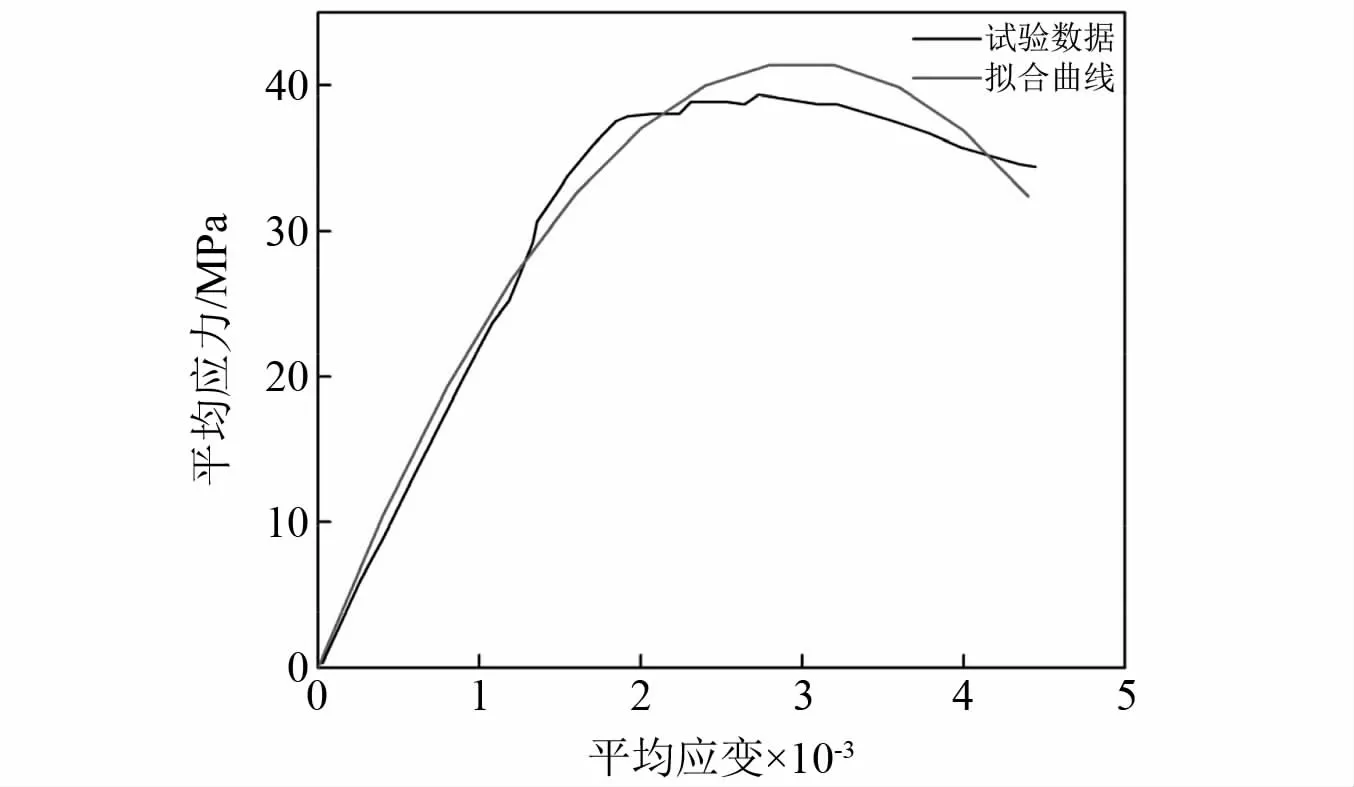
图3 材料本构曲线拟合效果Fig.3 Fitting effect of material constitutive curve

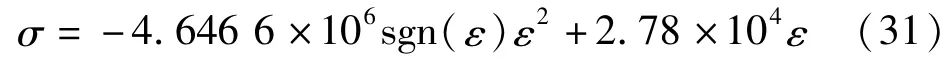
式（31）可视为普通钢筋混凝土结构采用的等效复合材料受压应力-应变全曲线表达式。

2.2 静力验证分析

上文对圆环形、箱形截面非线性悬臂杆在均布荷载、倒三角荷载和与惯性力相关荷载作用下的最优截面尺寸公式进行了推导求解，并得到解析解。但公式在结构处于弹性阶段及弹塑性阶段下的正确性及精度有待进一步验证。利用ANSYS有限元平台对截面尺寸按照上文公式分布的变截面非线性悬臂杆结构进行静力分析。

悬臂杆结构的基本设计参数为:结构总高度H为20 m，非线性材料初始弹性模量25.94 GPa，泊松比0.3，有限元模型沿结构高度方向均匀设置了21个节点，悬臂杆底面与地面固接，每个节点处布置一个截面，截面尺寸按照上节公式的结果设置，采用Beam188梁单元，该单元适合模拟Timoshenko梁，考虑剪切变形的影响，每个相邻节点之间设置taper变截面梁单元。按照求得的解析解，悬臂杆顶部截面面积应为0，然而ANSYS中梁单元不允许出现面积为0的截面，因此设顶部截面面积略大于0。材料本构采用KINH多线性随动强化模型，考虑包辛格效应，设置了11个数据点，包含了上升段、峰值点和下降段，以便对结构产生不同应变的情况进行模拟，验证公式的适用性和准确性。

对圆环形、箱形截面悬臂杆在均布荷载、倒三角荷载和与惯性力相关荷载作用下的结构响应进行分析，分为截面最大正应变分别为0.001，0.002和0.003的情况讨论，一共建立了7个悬臂杆结构模型，设计参数和工况如表1所示。

表1 悬臂杆结构的设计参数和工况Tab.1 Design parameters and working conditions of cantilever structures

由于材料本构中应力与应变一一对应，因此可以用应变分布表征应力分布，同时为了对比设计正应变g（σ1）与实际应变，故提取加载后有限元模型的Mises应变云图，如图4所示。由结果可见:若按相应的理论公式设置截面尺寸，变截面连续悬臂杆结构的确能够在各截面均能实现满应力分布，并且适用于结构的弹性和塑性阶段，验证了公式中关键参数的正确性。应变云图中结构顶部出现一定程度的应力集中，原因是在模型顶部设置了一个略大于0的面积后，该局部的实际值和理论值产生了误差。

图4 结构应变云图Fig.4 Strain nephogram of specimens

提取加载后结构全部单元的最大应变，如图5所示，所有构件应变云图趋势类似，高度15 m以下部分的应变均小于设计正应变g（σ1），这是由于有限元中提取的是Mises应变，结构横截面正应变是影响Mises应变的主要因素，因此Mises应变虽然分布均匀但在幅值上与正应变存在差异，此外，taper变截面梁单元上下截面之间存在线性变化，这与最优截面尺寸分布解析解之间存在一定误差。

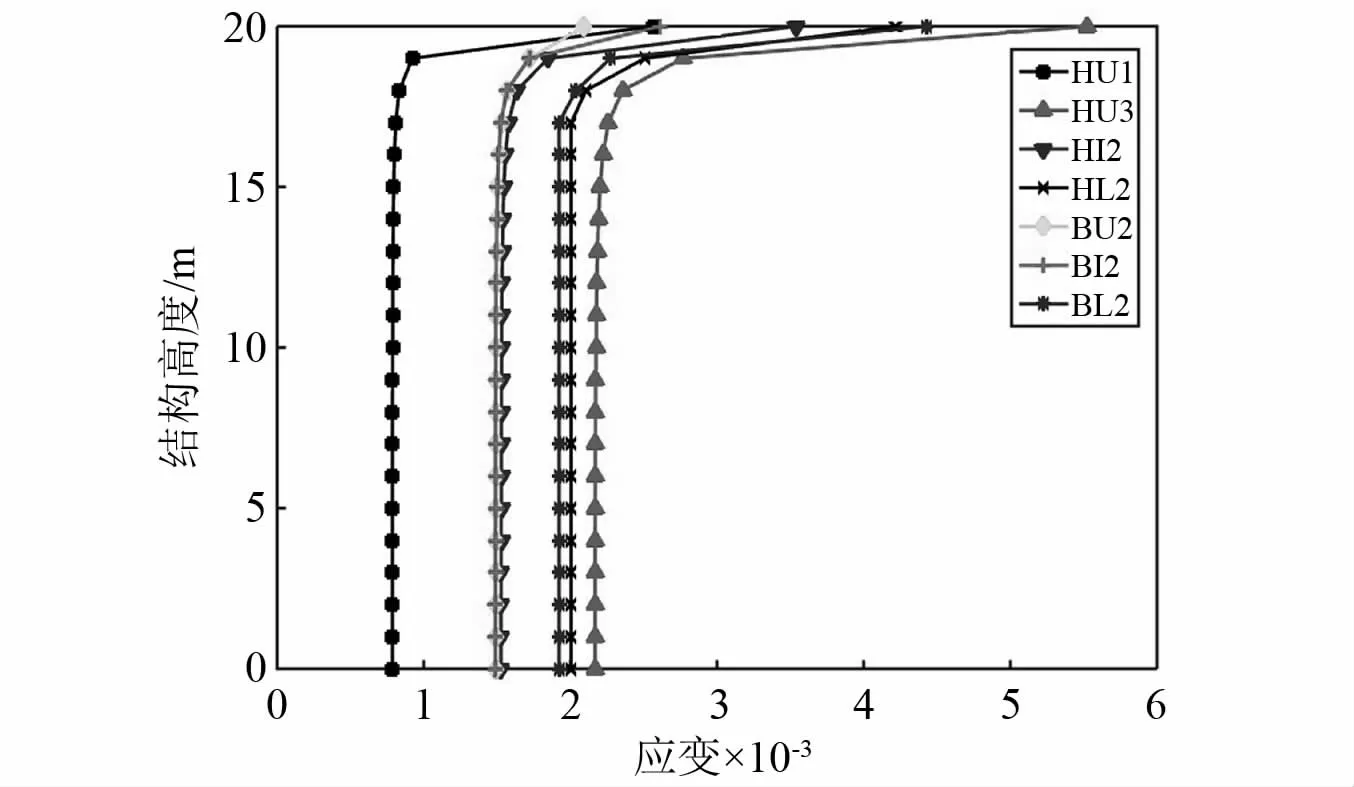
图5 结构应变分布Fig.5 Strain distribution of specimens

为了验证优化设计效果，在最大应变为0.001的情况下，将均布荷载作用下未经过优化的等截面悬臂杆结构与优化过的变截面悬臂杆结构HU1进行对比，等截面结构底面直径8 m，HU1底面直径9.38 m，α均取0.9。有限元模型参数除截面变化规律外与优化过的结构保持相同。另外，由于HU1出现顶部应力集中现象，设置一个顶部截面增大的构件，该构件顶部圆形截面直径0.085 m，HU1顶部截面直径0.05 m，其余参数相同，三者对比结果如图6所示。

图6 未优化结构与优化结构对比结果Fig.6 Comparison of optimized structure

从图6中可以看出，未经过优化的等截面悬臂杆结构应变呈明显的非均匀分布，底部应变大，随着结构高度增加，逐渐趋近于零，而优化过的变截面悬臂杆HU1虽然从15 m高度往上应变逐渐非线性增大，顶部出现一定的应力集中，但15 m以下应变基本相等，并且顶部应力集中现象可以通过增大顶部截面面积的方法解决，等截面结构体积为100.48 m3，应变分布均方差为4.5×10-4，顶部加强结构体积为85.56 m3，应变分布标准差为3.07×10-6，优化后结构体积减少了14.8%，应变分布明显更均匀，充分证明了该优化方法的优越性。

需要指出的是，在均布荷载和倒三角荷载作用下可以实现满应力准则的结构外观呈“外凸”型，而在与惯性力相关荷载作用下则呈“内凹”型，两者截然不同，悬臂杆结构模型如图7所示。在实际工程中，均布荷载（倒三角荷载）和与惯性力相关荷载可能共同作用于结构，可以根据不同的工程需求对两者赋予不同权重，如圆环形结构最优截面尺寸分布按式（32）计算

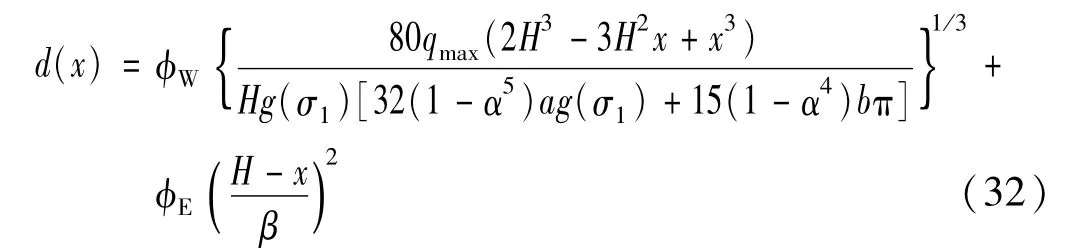
式中，ϕW和ϕE分别为倒三角荷载和与惯性力相关荷载的权重系数，ϕW+ϕE=1。当ϕW=ϕE=0.5时，悬臂杆模型如图7（c）所示。

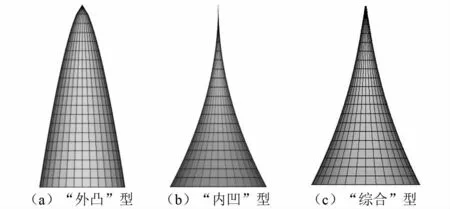
图7 变截面悬臂杆有限元模型Fig.7 Finite element model of variable section cantilever

2.3 动力验证分析

前述研究是在静力学基础上对地震动和风荷载作用下结构的截面尺寸分布进行优化。为了验证优化结果在动力作用下的准确性，对前文中顶部加强的悬臂杆结构进行动力时程分析。将优化后的圆环形和箱形截面悬臂结构和未优化过的等截面悬臂结构进行对比，对所有结构基底输入单向El Centro地震波，时间间隔0.02 s，持时15 s。由于在2.14 s时地震波加速度时程达到峰值，5.50 s时位移时程达到峰值，因此提取以上两个时刻的结构各节点应变，结果如图8和图9所示。分析结果可发现:在经过顶部加强后，优化后圆形和箱形截面悬臂杆在地震作用下的应变分布均匀，均实现了满应力准则；而未优化的等截面悬臂结构的应变分布则从底部到顶部非线性减小，应变分布离散性远大于优化后的悬臂杆结构。经进一步分析结果可确认优化结构的应变分布规律在任何时刻均相似，充分实现了满应力准则。综上，按与惯性力相关荷载进行优化的结构，在动力作用下也实现了满应力准则，且不同截面的优化结果均具有良好效果。

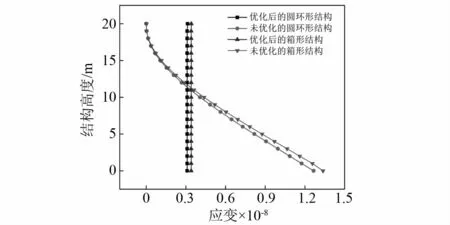
图8 地震动加速度最大峰值时结构应变分布Fig.7 Strain distribution under peak ground acceleration

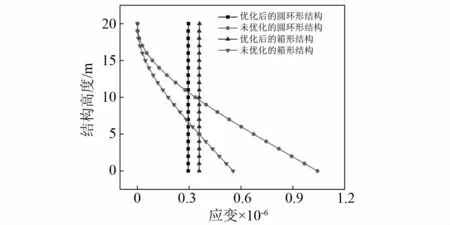
图9 震动位移最大峰值时结构应变分布Fig.9 Strain distribution under peak ground displacement

3 结构最优刚度分析

上文推导出了均布荷载、倒三角荷载和与惯性力相关荷载作用下圆环形、箱形截面悬臂杆结构的最优截面尺寸分布公式，并基于ANSYS有限元平台验证了按照该公式布置截面的结构可以在相应工况下实现满应力准则。其剪切刚度和弯曲刚度计算公式如下

按照式（33）和式（34）计算各种工况下公式对应的刚度，此结果可供实际工程设计和规范修订参考。

均布荷载作用下，圆环形截面悬臂杆剪切刚度和弯曲刚度为

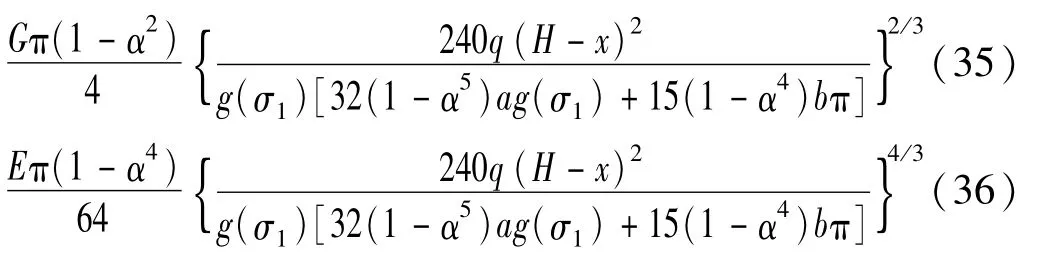
倒三角荷载作用下，圆环形截面悬臂杆剪切刚度和弯曲刚度为

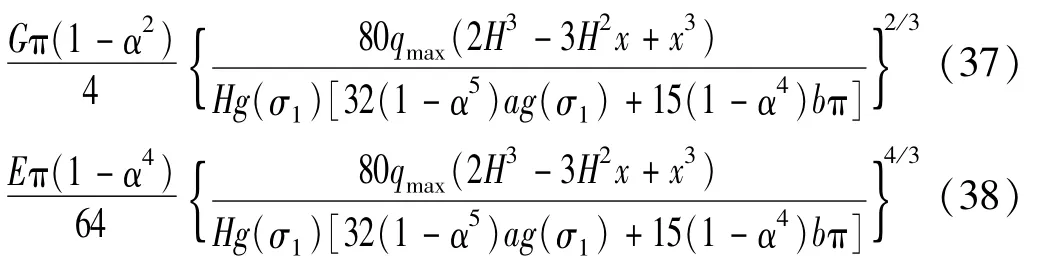
与惯性力相关荷载作用下，圆环形截面悬臂杆剪切刚度和弯曲刚度为

箱形截面悬臂杆结构的剪切刚度和弯曲刚度同理，不再赘述。

本文的理论方法和优化结果适用于诸如塔式结构和烟囱等连续体的静动力优化设计，也较适用于高细比较大的高层建筑等工程结构，相应的优化设计不必拘泥于截面固有形式，可根据结构截面尺寸或刚度的优化解析解进行适当调整，并可进一步通过调整抗侧力构件配筋和局部杆件截面尺寸等方式灵活调整结构抗侧刚度分布，使结构的等效参数与理论优化结果相近，实现满应力准则。与拓扑优化相比，本文方法不以材料取舍为手段，相应结果的区域边界满足连续性条件，更符合实际条件需求和限制，具有更好的工程可行性。此外，与何浩祥等以相对位移相等为优化目标的方法相比，本文结果与之相近但有所差别，且从材料应力水平真正实现了满应力分布，因此具有更严密的力学依据。

4 结 论

将工程结构简化为圆环形、箱形截面悬臂杆结构，以等应力为优化目标进行优化设计。将风荷载和地震作用等激励简化为均布荷载、倒三角荷载和与惯性力相关荷载，建立弯矩平衡方程求解，得到最优截面尺寸解析解，并获得最优剪切刚度和弯曲刚度分布。通过有限元模拟验证了解析解的正确性和适用性。得到以下结论:

（1）在弹性和弹塑性阶段，在指定荷载模式下的悬臂杆截面尺寸沿高度按本文获得的理论分布函数进行设置可以实现满应力。

（2）均布荷载和倒三角荷载作用下，按等应力理念优化设计的悬臂杆结构呈现“外凸”形状，而与惯性力相关荷载作用下的结构呈现“内凹”形状，两者截然相反，实际工程中，结构往往受到多种荷载同时作用，可以根据当地的工程需求对不同荷载的结果赋予不同权重进而获得组合荷载下的优化结果。

（3）基于ANSYS有限元平台，对各种工况下的悬臂杆最优截面尺寸公式分别进行了静力和动力优化验证。在静荷载作用下，按等应力优化设计的悬臂杆结构在弹性和弹塑性状态下除顶部出现应力集中现象外，其余部分均处于等应力状态，顶部应力集中问题可以通过增大顶部截面的方法解决。顶部经过加强后，按与惯性力相关荷载作用下优化结果设计的结构处于等应力状态，因此优化结果在动力荷载作用下同样有良好的效果。