新课标背景下的初高中数学衔接教学研究

富国柱

(湖南省株洲市外国语石峰学校 湖南株洲 412000)

一、初高中数学衔接教学概述

“衔接”，顾名思义，便是将前后两种属性相同的事物相互连接，初高中数学衔接教学是一种通过将初中数学与高中数学在内容、方法等方面进行连接与过渡的教学活动，其主要目的是确保学习上的连贯性，让学生能够以原有的数学知识为基础开展高中数学学习，有助于学生对数学的学习、理解。初中数学与高中数学不管是教学内容上还是学习活动中都存在一定的差异性，而学生进入高中阶段后，不仅需要接受新教材，还要适应新的教学环境及新集体，在新课标背景下，高中数学学科内容、结构等都与以往的数学教材有所差异，这也进一步导致初高中数学教学脱节问题日益突显。目前，面对新课标下的高中数学教学，部分学生对其产生排斥心理，加上有些学生的初中数学基础较为薄弱，导致高中数学学习更加吃力，教师在教学过程中也是较为困难。为此，初高中数学的衔接便能够有效稳定学生情绪，使学生在教师的引导下逐渐适应新的教材，进而不断提高数学成绩[1]。

二、新课标背景下初高中数学衔接教学的必要性

新课标背景下之所以要促进初高中数学衔接教学的开展，其必要性主要体现在以下几个方面。

其一，教材的变革与深化。高中数学教学活动的开展需要围绕教材进行，所以，教材是数学教学的载体，也是课程改革的重点内容，伴随课程改革的实施，新的教学理念也会随之出现，而新课程改革之后的高中数学教材尽管在难度上有了明显的降低之势，但相较于初中数学教材而言，其难度还是比较高的，高中数学教材特点具体体现在容量大、内容抽象以及起点高三个方面。1.高中阶段数学教材必修课本有五本，涉及高考考查的选修内容，理科有三本，文科有两本，并且，在高考选做题中还涉及选修4系列中的三本课本，这也进一步体现了高中数学容量大的特征，由此可以看出，高中数学教材在新课程改革之后其知识点有所增加，课容量也随之提升，进度上也需要加快，同时灵活性也有所提高。2.内容抽象的特点体现在新课标高中教材中包含大量的数学符号及数学术语，学生在学习过程中除了要理解这些符号与术语的含义，还要通过运用数学符号与术语开展推理与运算，这对于刚升入高中阶段，抽象能力比较弱的学生来说具有较大的学习难度[2]。3.起点高特点主要体现在数学教材编排体系上，“函数”与“空间立体几何”都在高一学年教材上，与学生的接受能力与思维水平不一致，进而出现知识脱节与能力断层等问题，尽管高中数学教材缩减了很多内容，但由于受到高考的牵制，教师在教学中也不敢随意降低教学难度，所以，针对高中数学教学，非常有必要实现初中与高中数学教材的相互衔接，以此构建起知识间的联系，实现知识的过渡。

其二，思维方式与思维习惯的不同。学生思维的发展具有年龄与阶段性特征，初中阶段的学生其数学思维主要以形象思维与经验型思维为主导，而高中阶段的学生主要以理论型与抽象性思维为主，并逐渐朝着辩证思维方向不断发展，初中升入高中之后，学生在数学学习中会出现思维层次上的跳跃，进而导致学生产生不适感。为此，以初高中数学衔接教学，通过采用螺旋式教学方式等来实现学生思维方式及其思维习惯的过渡，在循序渐进中培养学生的抽象思维，这也进一步说明初中与高中数学衔接教学的必要性。

其三，学法与教法的改变。初中阶段的数学教师一般都讲解得比较细致，还会引导学生进行知识的归纳，学生在考试时只需要准确记住概念、公式等，并熟知教师所讲的同类型例题便可以取得较好的成绩，因此，初中学生的学习往往需要依靠于教师，其自主学习能力、独立思考及归纳总结等方面较为缺乏。进入高中阶段之后，数学教材内容的增多导致教师并不会对所教知识进行更细化的讲解，并且只会选择典型题型进行讲解，在教学方法上以设导、启发等为主，注重对学生独立思考能力及思维品质的培养，这就会让刚进入高中阶段的学生在学习习惯及教法上产生不适应感，在听课过程中也会出现思维障碍，常常会跟不上教师的思维。同时，在教学过程中，针对新课标数学教学，教师盲目提高教学标准，增加教学难度，与学生的认知结构产生冲突，不利于学生的数学学习，这就需要教师改变教学方法，采用初高数学衔接教学，帮助学生逐渐适应新教材，并从学生的认知结构出发，以旧知识为基础为新知识的学习提供保障[3]。

三、新课标背景下初高中数学衔接教学策略

（一）初高中数学衔接教学之知识衔接

心理学家皮亚杰曾经提出：“个体在遇到新的刺激时，总是会尝试着用原有的认知结构去同化它，以此来达到平衡，而同化与顺应之间的平衡是引起认知结构的一种新建构。”新课标高中数学教材尽管删减了一些内容，但在总体的内容容量上还是比较大的，这对于刚上升到高中阶段的学生来说往往会出现知识上的脱节，所以，针对新课程改革背景下的初高中数学衔接教学，教师一定要先从知识上进行有效衔接，并结合学生的认知水平与思维结构，通过新旧知识的衔接对学生的认知结构进行不断的优化，这样也有助于学生思维的转变。例如，人教版高中必修二，第三章直线与方程的第二节的复习课，该节知识目标为利用直线方程的五种形式求解直线方程，而五种直线方程的形式主要包括点斜式、斜截式、两点式、截距式、一般式，其中的一般式Ax＋By＋C＝0(A，B不全为0)与初中接触到的二元一次方程内容有关联，为此，教师可以给出例题作为导入，进而实现内容上的衔接。

例题：点O为坐标原点，平面镜OQ可以绕点O旋转，且OQ的长为3，点B在轴y上，当平面镜OQ在y轴负半轴上，点B是OQ的中点，此时从点A(3,0)发射的激光恰好能打到点B处，且激光照射的方向始终不会发生变化，求入射光线AB的直线方程。如图。

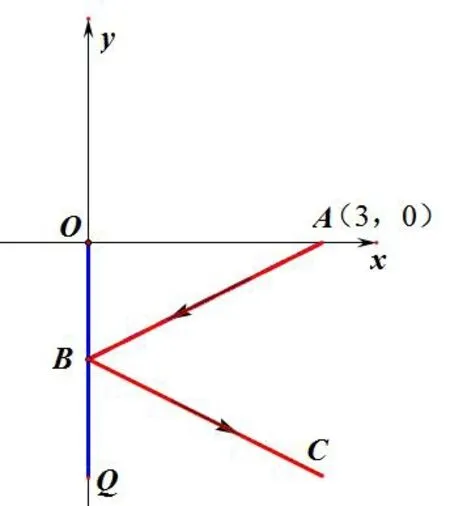
以例题为引导，让学生结合初中二元一次方程、直角坐标系等知识点求出入射光线AB的直线方程，进而引出直线方程的一般式，通过知识上的衔接构建起初中与高中数学的联系，进而逐步实现知识上的过渡，为学生的数学学习奠定基础。

（二）初高中数学衔接教学之学法衔接

个体差异性体现在学生的每个阶段，这也导致每个学生在数学学习中所采用的学习方法各不相同，由于学习方法是学生根据自身能力与认知而选用的一种对数学知识进行内化与理解的方式，初中学生在数学学习上会常常依赖于教师的总结与归纳，高中阶段数学教学旨在培养学生的独立思考能力、数学思维等，所以，进入高中时期之后，大多数学生倘若依旧采用初中时期的数学学法，必定会跟不上高中教师的数学教学思维。为此，基于新课标背景的高中数学教学，需要教师引导学生通过学法上的衔接促进初高中数学的有效衔接，以便让刚进入高中阶段的高一年级学生在学法上能够逐步接受内容较多的新教材知识。一般的学习步骤主要分为制定计划、课前自学、专心上课、及时复习、独立作业、解决疑难、课堂小结，简单来说便是预习、上课、整理、作业以及复习总结，例如，“直线方程的应用”教学复习中，教师可以组织学生自主对知识点进行归纳与总结，让学生在教师的逐步引导下独立对重点知识进行归纳总结，并在此过程中对学生的疑难问题进行回答，这样既可以培养学生独立思考与归纳的能力，又能让学生养成良好的学习习惯。如，针对直线方程的应用复习，在开始阶段可以先安排学生结合学案自主进行学习，之后根据设置的问题引导学生进行知识小结，随后让学生通过自主学习的方式继续探究，学生对学案中设置的问题逐步解答之后，则引导学生进行知识点的归纳与总结，让学生在此过程中逐渐养成独立思考及归纳总结的能力，从依靠教师归纳过渡到独立归纳与思考，进而实现学法上的衔接[4]。

（三）初高中数学衔接教学之教法衔接

初中阶段的数学教学教师一般都会对知识点进行较为细致的讲解，而高中数学由于新课标教材中知识容量的增加，大多会采用引导的方式开展教学，刚进入高中阶段的学生不管是认知能力还是思维能力上都会出现明显的不足，进而导致知识与思维上的断层。所以，针对高中数学教学，教师需要通过教法上的衔接来帮助学生实现知识上的过渡，例如，生活式教学法、新旧结合教学等，从学生的认知基础与思维结构出发，通过教法上的衔接促进学生高中数学能力的进一步发展。

四、结束语

总而言之，高一年级是初高中数学衔接教学的关键阶段，该阶段的学生刚刚进入高中阶段，对初中时期的数学还有一定的记忆，所以，开展初高中数学衔接教学既可以帮助学生对初中知识进行巩固，还可以为高中数学学习奠定基础，进而顺利过渡到高中学习中，促使学生尽快完成初中到高中角色的转变，并从学生的认知基础与学习能力出发，选择与高中数学内容紧密相连的初中知识，让学生在循序渐进中实现思维的层层递进与跃迁，以此提高学生的数学能力。