基于风速分段的DFIG机组综合调频控制研究

杨仁杰

(国网安徽省电力有限公司检修分公司， 安徽 合肥 230000)

0 引言

传统的双馈风力发电机组(Doubly-Fed Induction Wind Power Generator, DFIG)运行控制方法是采用MPPT模式，加之DFIG的有功和无功与电网解耦，当系统发生负荷扰动时，DFIG无法像同步机一样快速释放功率响应系统频率变化[1-3]，随着大规模风电并网，对电力系统稳定运行与控制产生较大冲击，本文介绍风电参与电网调频控制方法，再根据风电机组的减载水平使风电机组留有功率备用参与系统调频，对风速进行分段，为低风速段、中风速段以及高风速段，设计有功功率控制环节控制器，使得风电机组通过减载运行留有功率备用参与到系统调频中，提高风电的消纳能力并保证电力系统的稳定运行与控制，为碳达峰、碳中和贡献力量。

1 DFIG调频原理

为了兼顾虚拟惯性控制在暂态过程中的快速性以及下垂控制短暂的有功支撑改善频率偏差值提出了一种综合惯性控制，在有功功率控制系统同时引入频率偏差信号与频率变化率信号累加求和，这种控制方式可以进一步改善风机的频率响应能力，该方法的有功参考值如式(1)所示[4]。

(1)

式中，Kpf为下垂系数，Kdf为惯性系数，Δf为频率偏差，ΔP为有功增量，P为综合惯性控制有功参考值。图1给出了综合惯性控制原理框图。

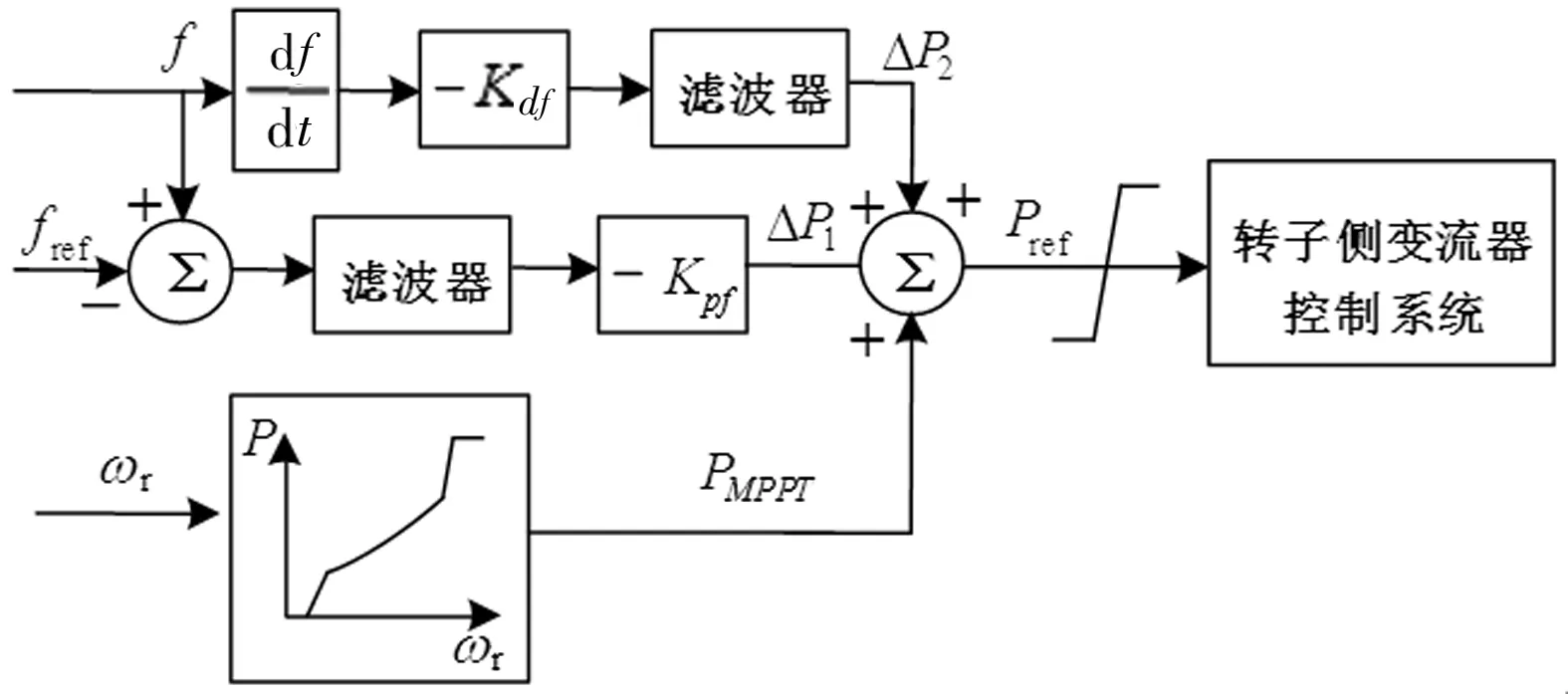
图1 综合惯性控制原理框图

当风机运行于最大功率追踪区域，DFIG的最大有功出力为Popt，当采用超速减载时，使得DFIG运行于超速减载曲线的次优功率运行点，定义风电场的减载水平系数为k%，则实行限功率后其有功出力值为：

(2)

式中，Pdel为减载k%时DFIG的有功输出参考值，Cpdel为减载运行时的风能捕获系数，进而定义次优功率追踪曲线转速-机械功率比例系数kdel为：

(3)

图2给出了处于次优功率追踪曲线下DFIG转子转速与机械功率原理图。

图2 超速减载控制次优功率曲线原理图

由图2分析，超速减载后的有功输出参考值Pdel_ωr[5]：

(4)

式中，PA1为超速减载运行时A点的有功输出，PB1为减载运行是B点的有功出力。

当风机运行于最大功率追踪模式时，在转子转速一定的情况下，不同的桨距角βi对应着不同的输出功率，且随着桨距角的增大风机出力减小，因此风机可以通过调整桨距角βi从而留有功率备用参与系统的调频控制。图3为不同桨距角时转速恒为βopt时风轮机特性曲线簇。

图3 不同桨距角所对应的风轮机特性曲线簇

当转子转速为ωopt时，P1为β1=0时最大功率追踪模式下的最大机械功率，随着β1至β3等间隔递增，在同一最优转子转速下ωopt情况下风轮机的机械功率Pm随着转速β发生相应的变化。当运行于MPPT模式下，变桨距风轮机存在唯一使得Cp取得极大值满足：

Cp(λopt(βi),βi)=Cp(βi)

(5)

从而最优叶尖速比λopt(βi)满足以下关系：

(6)

由于1点位于极佳功率曲线Popt1，故有：

(7)

假设桨距角减载水平为k%，则相同风速下可知变桨减载后风轮机输出的机械能Pdel为：

(8)

式(8)表明，减载水平为k%与桨距角βi有关。调整桨距角βi可使得系统留有一定的功率备用在承担调频任务时对系统进行长期的有功支撑。假定初始桨距角为βm，可推出满足一定减载比例的预置桨距角βm：

(9)

2 计及调频适应性的综合调频控制方案

2.1 基于减载水平的不同风速工况分区

当在额定风速以下超速减载不能完全实现k%水平的减载时(一般为10%～20%)，就要协助桨距角进行频率调节，此时：

Pdel=Pdel_ωr+Pdel_β

(10)

假设超速减载之后，转子转速达到最大值ωmax，此时对应的风轮机输出功率为Pa，根据此时的Pa求解出减载前的功率Pb，其满足：

Pa=(1-k%)Pb

(11)

由于减载前时风机仍然未达到最大转速，采用MPPT运行模式，稳定运行时桨距角为0，根据风机最大功率追踪曲线得到相应的转子转速ω0，其满足：

(12)

式中，v0为减载比例系数为k%时DFIG的超速减载临界风速，进而推出：

(13)

进而可以推出此时风能捕获利用系数Cp：

(14)

由于此时Pb为已知量，可知定比例减载系数的超速减载临界风速v0与ω0以及Pb满足下式：

(15)

因为Pb与ω0已知，进而可以逆向求出减载比例为k%时超速减载的临界风速v0。当v小于v0，可以通过超速减载实现k%的减载，当v大于v0时无法通过超速减载实现k%的减载，进而需要借助桨距角控制协通超速减载实现k%的减载，随着风速进一步上升，风电机组转子转速达到ωmax，此时风机的超速减载控制失效，仅通过变桨控制实现k%的减载。

2.2 基于转子动能与功率备用协调控制的综合调频控制方案

由前文可知在不同减载水平下以及不同的风速区间段风电机组实现限功率运行留有功率备用的控制方法不同，当系统发生负荷扰动时需要调用这部分功率备用，相反只需在各个风速区间段通过附加有功控制环节将这部分功率调用出来即可，考虑到转子动能控制可以使DFIG表现出类似于同步发电机组的惯性响应能力，响应速度快，在上文分析的基础上设计了一种计及风速分段以及调频适应性的综合调频方案，图4给出了基于一定减载水平的风速分区有功功率控制图。

图4 基于减载水平的风速分区有功功率控制图

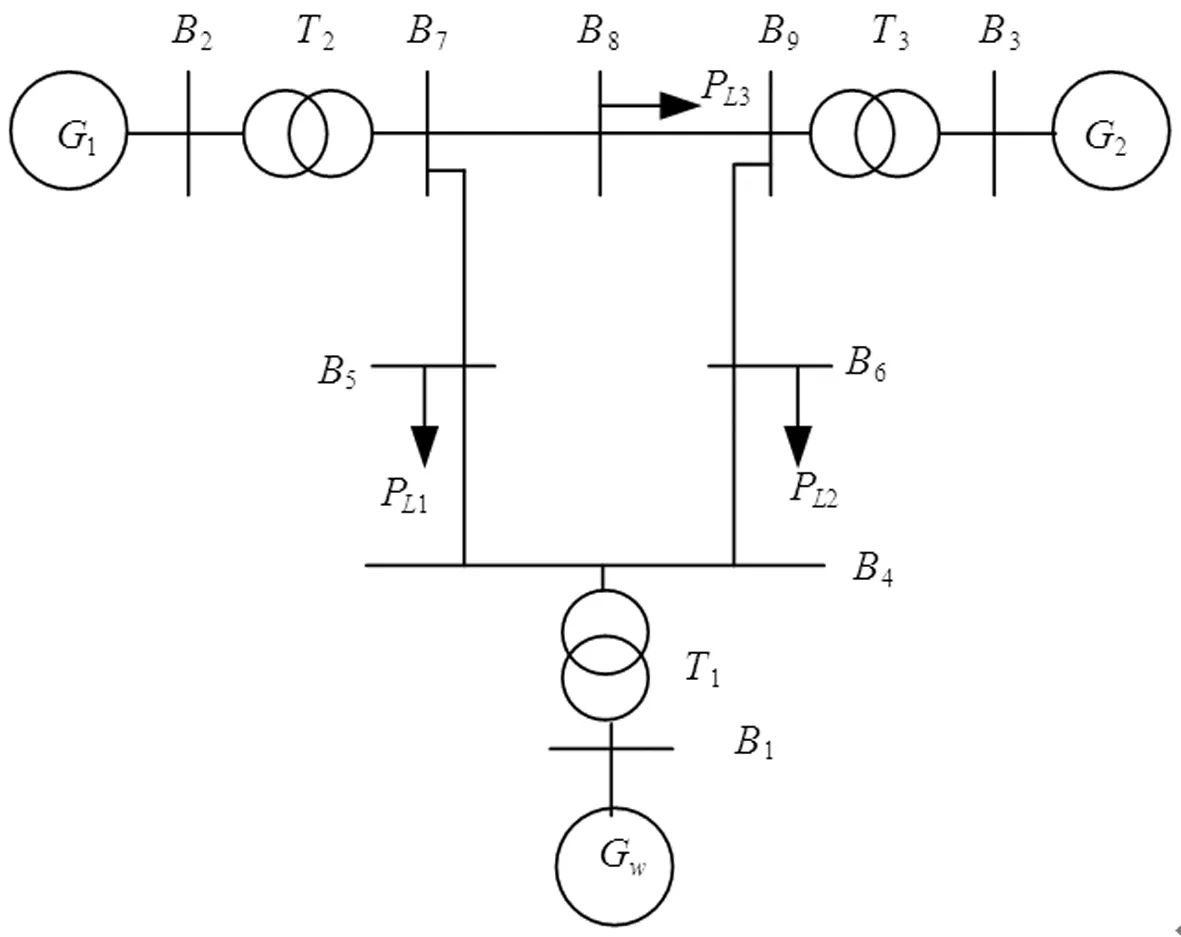
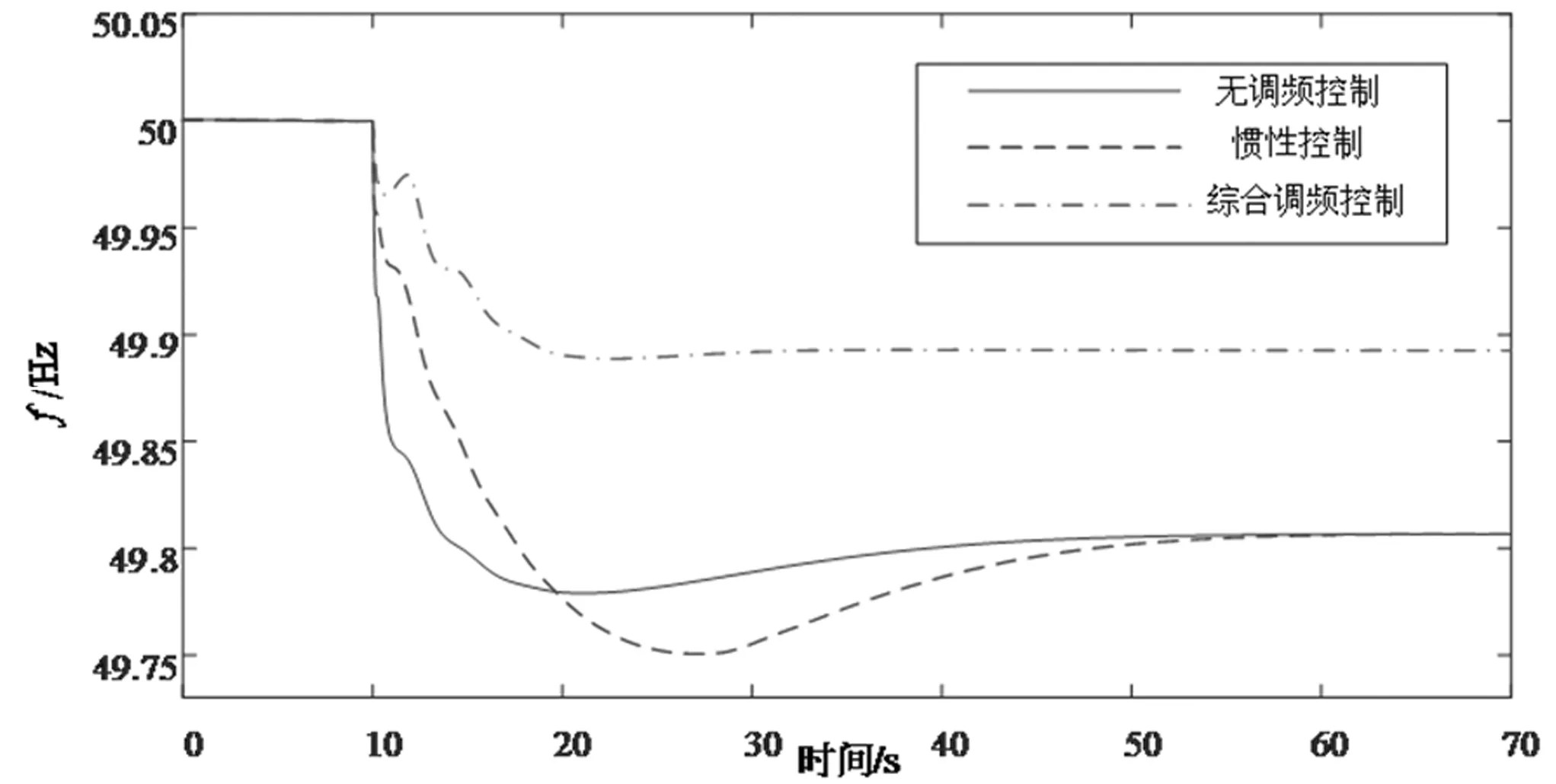
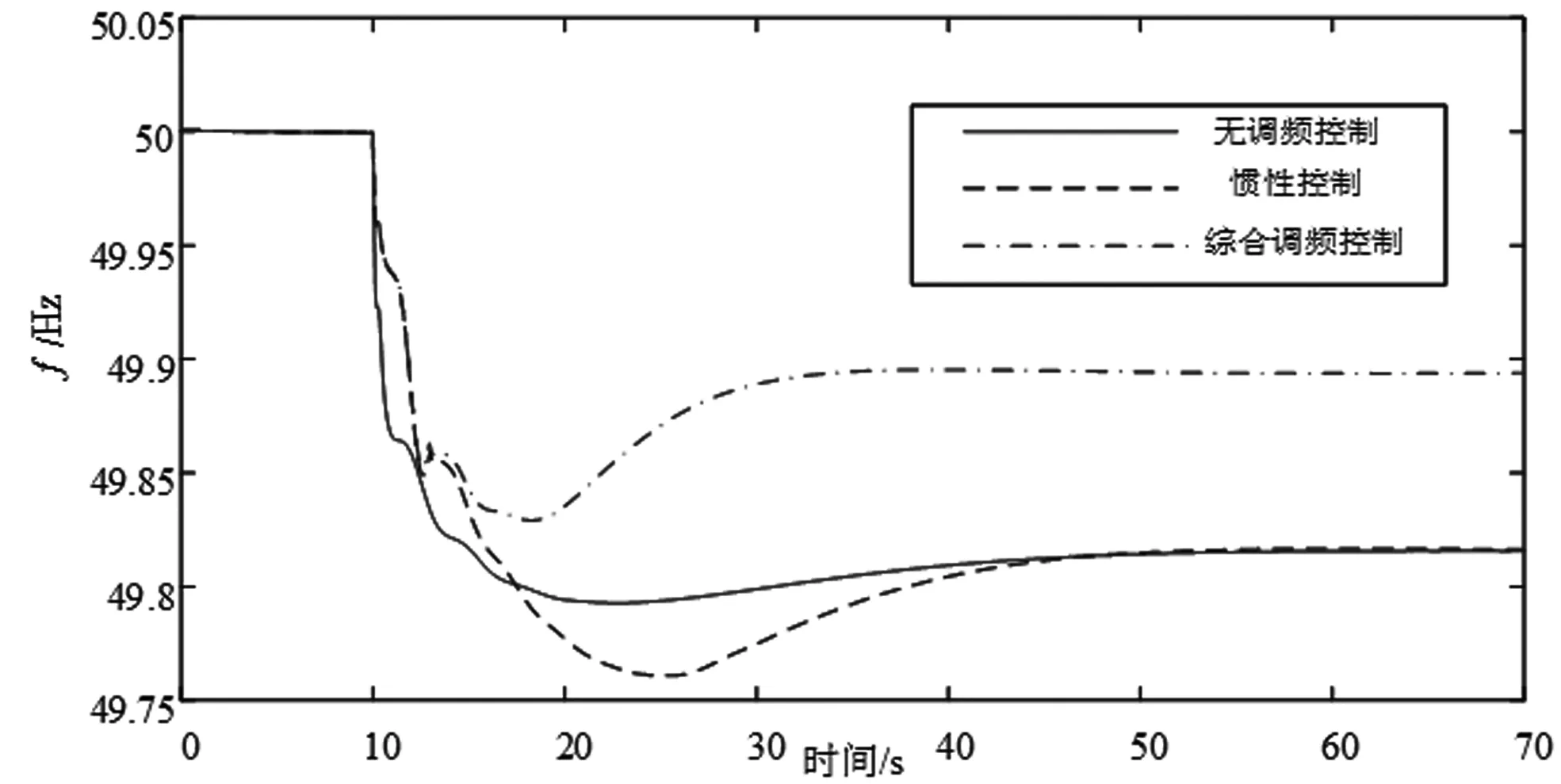
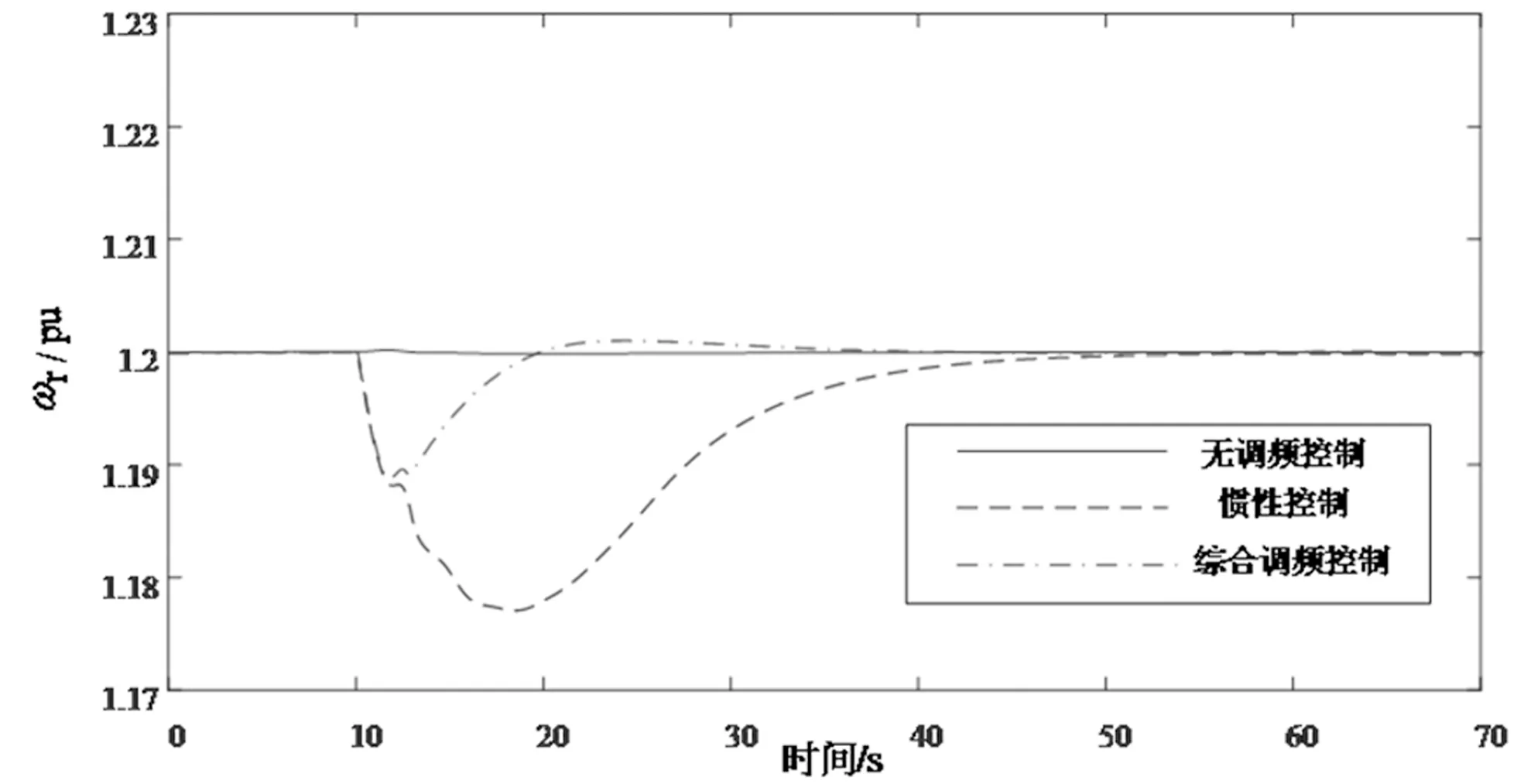
当v

图5给出了结合转子动能控制与功率备用控制的综合控制框图。

图5 计及调频适应性的综合调频控制方案

其中桨距角控制机构的频率响应满足：

Δβ=KβΔf

(16)

式中，Δβ为中风速与高风速桨距角控制动作响应系统频率变化Δf的桨距角变化量，Kβ为比例系数。

超速减载留有的功率备用对系统的有功支撑满足下式：

(17)

式中，Ki与Kp分别为附加有功控制器的积分系数与比例系数。

3 仿真分析

本章节基于MATLAB/Simulink平台改进了3机9节点电网仿真模型如图6所示，将一个额定容量为100 MW的DFIG机组Gw替换到元模型中的功率平衡节点，2个额定容量为100 MW的同步发电机组G1与G2，DFIG的额定运行风速为12 m/s，在仿真10 s时系统的负荷PL1增加30 MW，在仿真过程中取DFIG的减载水平为20%，为了验证上文中所提出的综合调频控制的有效性，分别在低风速、中风速以及高风速三种不同的风速工况进行仿真验证。

图6 3机9节点电网结构图

3.1 低风速工况下仿真分析

设置低风速工况下的风速为10 m/s，此时DFIG机组仅通过超速减载留有有功备用，在仿真10 s时有功负荷负荷PL1增加30 MW。图7为DFIG在低风速工况下运行时DFIG不参与系统调频、采用惯性控制以及采用综合调频控制时系统的频率变化图。

图7 低风速工况下系统频率动态响应图

在10 s时系统的有功负荷增加30 MW，当风电机组不参与调频时，系统频率最大频率偏差为0.23 Hz，一度跌落至49.77 Hz，在负荷扰动发生50 s后频率最终稳定在49.8 Hz。当采用惯性控制时，在系统频率变化的初期会一定程度上缓解系统频率下跌的速度，但相较于DFIG不参与调频时，无法改善系统频率稳态偏差。当采用综合调频控制时，DFIG通过转子动能控制以及有功备有控制迅速释放转子中所存储的旋转动能提供有功支撑，加之有功备用控制可以对系统进行长期支撑，所以相较于风机不参与调频时系统的频率得到了改善，由稳态时的49.8 Hz提升到49.83 HZ，频率进入稳态时间相较于惯性控制以及无调频控制快了10 s左右。因此当风机采用综合调频控制参与系统频率调节时，由于其快速的有功爬坡能力会快速响应系统频率变化，改善较大负荷扰动时的频率变化，保证电力系统安全稳定运行与控制。

图8表示DFIG机组的转子转速动态响应图。当DFIG不参与调频其转子转速维持在1.128 pu，当采用惯性控制时，在频率变化初期，附加的惯性控制使其转子转子减小释放旋转动能，在扰动发生后的17 s下降至1.1 pu，此后需要从电网吸收功率来进行转速恢复。当采用综合调频控制时。当系统频率下跌，附加有功控制环节控制其转子转速释放旋转动能，此时转子转速会减小到1.05 pu，由于超速减载的有功备用也是长时间的有功支撑，故相较于传统的惯性控制其转子转速不会恢复至转速控制前的参考值，进而不存在系统频率二次跌落问题，从而验证了低风速采用综合调频控制的正确性。

图8 低风速工况下DFIG转子转速动态响应图

3.2 中风速工况下仿真分析

设置中风速工况下的风速为11 m/s，此时DFIG机组通过超速减载以及桨距角减载控制留有有功备用，在仿真10 s时有功负荷负荷PL1增加30 MW，系统频率变化、各同步发电机组的有功出力、DFIG机组的有功出力、桨距角变化以及转子转速的动态响应图分别如图9～11所示。

图9为DFIG在中风速工况下运行时DFIG不参与系统调频、采用惯性控制以及采用综合控制时系统的频率变化图。

图9 中风速工况下系统频率动态响应图

在10 s时系统的有功负荷增加30 MW时，若DFIG不参与系统的频率调节，频率最大偏差为0.22 Hz，影响电力系统的稳定运行与控制，在扰动发生后50 s系统频率稳定在49.81 Hz，稳态偏差为0.19 Hz。当采用惯性控制时，在系统频率变化的初期会一定程度上缓解系统频率下跌的速度，但最大频率偏差为0.25 Hz，在扰动发生后60 s系统频率稳定在49.81 Hz，无法改善系统频率稳态偏差。当采用综合调频控制时，DFIG在转子动能控制以及有功备用控制的转子转速控制与变桨距角协调控制下，系统频率由DFIG不参与调频时的49.78 Hz提高到49.89 Hz，且调频速度相较于无调频控制快了20 s。因此中风速通过采用综合调频控制可对系统提供长时间的有功支撑。

图10～11分别表示DFIG在中风速工况下运行时DFIG不参与系统调频、采用惯性控制以及采用综合调频控制时DFIG机组的桨距角以及转子转速动态响应图。

图10 中风速工况下DFIG机组桨距角变化动态响应图

图11 中风速工况下DFIG机组的转子转速动态响应图

在DFIG不参与系统调频时，DFIG的桨距角稳定在4°，转子转速维持在1.172 pu。当采用惯性控制时，其桨距角相较于无调频控制无变化，转子转速在附加的惯性控制情况下转速减小释放动能，在负荷扰动发生10 s后下降至1.136 pu，随后从电网吸收功率恢复转速至扰动发生前的1.172 pu。当采用综合调频控制时，由于转子转速超速减载留有一定的功率备用，在10 s系统扰动发生后，通过转子动能控制以及功率备用控制协调控制释放转子动能，增大DFIG的有功出力，转子转速降低至1.104 pu，同时，桨距角在桨距角控制下减小桨距角增大风机出力，桨距角由不参与调频时的4°变化至1.423°，响应系统频率变化，验证了中风速段综合调频控制正确性。

3.3 高风速工况下仿真分析

设置高风速工况下的风速为15 m/s，此时DFIG机组通过桨距角减载控制留有有功备用，在仿真10 s时有功负荷负荷PL1增加30 MW。

图12为DFIG在高风速工况下运行时DFIG不参与系统调频、采用惯性控制以及采用综合控制时系统的频率变化图。

图12 高风速工况下系统频率动态响应图

在10 s时系统发生有功负荷扰动，当DFIG不参与调频时，系统频率最大偏差为0.21 Hz，稳态偏差为0.19 Hz。当采用惯性控制时，在系统频率变化的初期会一定程度上缓解系统频率下跌的速度，但最大频率偏差为0.24 Hz，在扰动发生后50 s系统频率稳定在49.81 Hz，无法改善系统频率稳态偏差。当采用综合调频控制时，在调频初期在惯性控制作用下频率下跌速度得到一定程度上的缓解，随后采用变桨控制将有功备用释放出来，由于桨距角惯性时间常数大，在频率下跌的初期无法进行相应的有功支撑，但由于桨距角控制有功调节范围大，DFIG参与调频时频率最大偏差较不参与调频时高0.08 Hz，并最终稳定在49.89 Hz，且调频速度相较于无调频控制快了15 s，显著的改善了系统的频率变化，验证了该策略的有效性以及桨距角控制有功调节范围广。

图13～14分别表示DFIG在高风速工况下运行时DFIG不参与系统调频、采用惯性控制以及采用综合调频控制时DFIG机组的桨距角以及转子转速动态响应图。

图13 高风速工况下DFIG机组的桨距角变化响应图

在DFIG不参与系统调频时，DFIG的桨距角稳定在9.33°，转子转速维持在1.2 pu。当采用惯性控制时，其桨距角相较于无调频控制无变化，转子转速在附加的惯性控制情况下转速减小释放动能，在负荷扰动发生10 s后下降0.023 pu至1.177 pu，随后从电网吸收功率恢复转速至扰动发生前的1.2 pu。当采用综合调频控制时，其转子转速下降至1.188 pu，随后缓慢上升直到1.2 pu，与此同时，由变桨控制所存储的有功备用得以释放，桨距角由初始时刻9.33°减小到7.736°，有功出力随着桨距角的减小而增大，响应系统频率变化，验证了高风速段综合调频控制正确性。

图14 高风速工况下DFIG机组的转子转速变化响应图

通过对比图7、图9、图12不同风速工况下系统频率动态响应图可知，当处于低风速的风电机组只能采用超速减载控制留有功率备用，且风电机组的有功出力值偏低，虽然一定程度上提高了系统的稳态频率，但对比中风速以及高风速工况下可知，采用变桨控制留有功率备用更大，对系统稳态频率贡献大。

4 结论

本文首先通过分析DFIG参与电网频率调节的数学原理，针对风电机组减载水平划分风速区间段，分别在不同风速区间段采用不同的控制方式，设计了一种计及调频适应性的综合调频控制方案，可以使得转子动能控制与有功备用控制灵活结合，在低风速段采用综合惯性控制与超速减载控制的协调控制方式，可以充分发挥惯性控制的快速性以及有功备用控制的持久性，在中风速段，考虑到仅仅通过超速减载控制无法实现定减载水平的有功备用，因此需要协调变桨控制，从而结合综合惯性控制实现DFIG快速持久地参与到系统的频率调节中，在高风速段，附加惯性与变桨控制协同控制使得DFIG参与到系统频率调节中，通过仿真验证了所提出的综合调频控制的有效性。