921A钢在海水中腐蚀的力学化学效应*

王向军，徐庆林，宋玉苏，王海光

(1. 海军工程大学 电气工程学院， 湖北 武汉 430033； 2. 海军工程大学 基础部， 湖北 武汉 430033)

船舶和海洋工程结构的复杂性及其服役环境的特殊性，使得结构产生复杂的应力应变，如肋骨与船体的焊接处和船体表面的腐蚀缺陷处等都会产生应力集中[1-3]。另外，潜艇在下潜与上浮的过程中[4]，结构应力会随着静水压力的变化而发生显著的变化。载荷和腐蚀介质的交互作用被定义为金属腐蚀的力学化学效应，它主要包括在载荷和腐蚀介质的协同作用下金属腐蚀电位的降低和腐蚀速率的增大[5-6]。杨宏启等[7]的研究表明，在应力接近160 MPa时，Q235B钢在3.5%NaCl溶液中的腐蚀速率增大了约44%，因此金属在海水中腐蚀的力学化学效应不容忽视。

Gutman所著的《固体表面的力学化学》系统阐述了金属力学化学现象及其内在的规律，该书的出版，引起了学者们对金属在腐蚀介质和应力协同作用下力学化学行为的高度关注，并针对此问题展开了大量的研究[8-14]。已有的关于金属腐蚀力学化学方面的研究主要存在以下三点不足：第一，虽然Gutman[15]从热力学角度理论分析了压缩载荷和拉伸载荷对力学化学效应的影响具有对称性，但基本上是基于拉伸载荷展开的[7,10,16-17]，很少涉及压缩载荷对力学化学效应的影响；第二，在研究塑性变形范围内的力学化学效应时，通常采用外加载荷、冷加工或焊接等方法使金属产生残余塑性应变[8,12,18]，再研究残余变形金属在腐蚀介质中的腐蚀行为，这并不是真正意义上的载荷与腐蚀介质的协同作用；第三，目前对力学化学效应的研究主要集中在不锈钢和管线钢[17,19-21]，而针对船舶及海洋工程结构常用的高强低合金钢则研究较少。

本文采用电化学测试技术并结合金属腐蚀的力学化学理论分析了船用921A钢在载荷与腐蚀介质协同作用下的腐蚀行为，得到了弹性拉应力、弹性压应力和弹塑性应变对力学化学效应的影响规律，采用自制的载荷-电化学实验装置实现了塑性变形与腐蚀介质协同作用下的电化学性能测试。

1 实验方法

1.1 试样和电解液

试样材料为船用921A钢，其化学成分(质量分数)为：C=0.07%～0.14%; Si=0.17%～0.37%; Mn=0.30%～0.60%; S≤0.015%; P≤0.020%; Ni=2.60%～3.00%; Cr=0.90%～1.20%; Mo=0.20%～0.27%; V=0.04%～0.10%; Fe余量。试样尺寸如图1(a)所示，厚度为1.2 mm，电化学性能测试的试样焊接导线，在试样中间留出1 cm长度的工作面，非工作面用环氧树脂进行密封处理，如图1(b)所示，工作面用SiC湿砂纸逐级打磨至1 000目，丙酮脱脂，并依次用乙醇和蒸馏水冲洗，然后置于干燥箱中烘干。电化学实验的电解液为模拟海水，由JENIKA深礁实验室晶体珊瑚海盐与蒸馏水按照质量比为1 ∶30的比例配置而成，溶液pH为8.0～8.3。

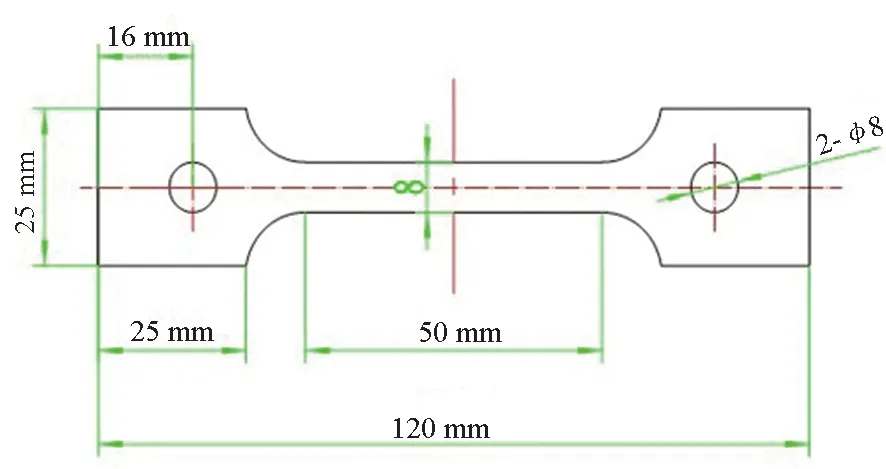
(a) 试样尺寸(a) Specimen size

1.2 电化学性能测试

自制的载荷-电化学实验装置如图2(a)所示，以实现载荷和腐蚀介质协同作用时的电化学性能测试。采用减速机对载荷进行放大，并通过机械装置加载到试样上，力传感器的测量范围为±15 kN，传感器配备数字显示器便于精确显示试样上所施加的载荷值，载荷达到屈服强度(640 MPa)后，通过位移量计算试样产生的塑性应变。本研究的弹性拉应力分别为0 MPa，100 MPa，200 MPa，300 MPa，400 MPa和550 MPa，由于试样厚度为1.2 mm，加载较大的压缩载荷时，试样发生明显的屈曲，故只进行了100 MPa和200 MPa的弹性压应力实验，弹塑性应变分别为1.0%，1.4%，1.8%，2.2%，2.6%和3.0%。

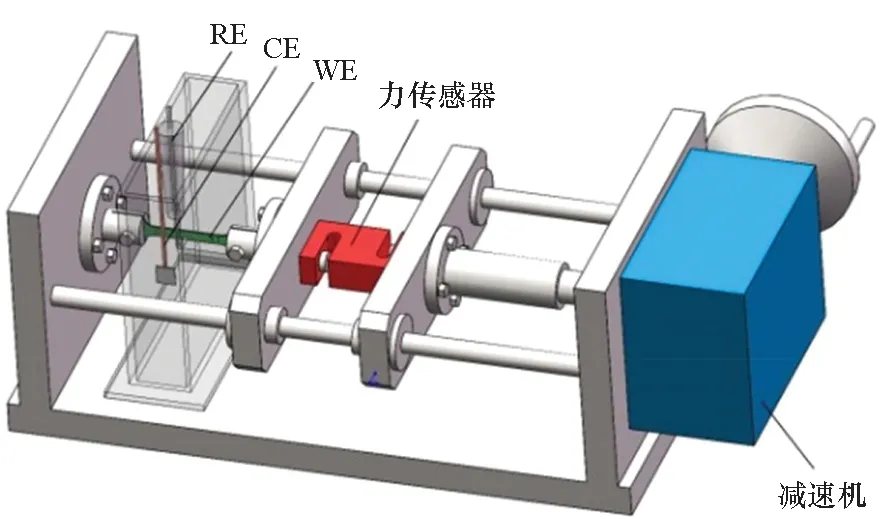
(a) 载荷-电化学实验装置(a) Load electrochemical experimental device

采用三电极体系在CS310电化学工作站上进行开路电位、动电位极化曲线和电化学阻抗谱(Electrochemical Impedance Spectroscopy, EIS)测试，实验整体布置如图2(b)所示。工作电极(Work Electrode, WE)为2.1节所述的电化学测试试样，参比电极(Reference Electrode, RE)为Ag/AgCl电极，填充溶液为饱和KCl，辅助电极(Counter Electrode, CE)为铂片电极(面积为1 cm2)。开路电位测试的采样频率为1 Hz，测试时间为3 500 s；极化曲线测试的电位扫描范围为-1.2～-0.2 V(相对参比电极)，扫描速率为1.0 mV/s；电化学阻抗谱测试的直流电位设定为921A钢在相应的应力状态下的腐蚀电位，外加正弦扰动信号的幅值为10 mV，频率扫描范围为105～10-2Hz(高频到低频)，并采用ZView软件对电化学阻抗谱进行拟合。

2 结果与分析

2.1 弹性应力对921A钢腐蚀行为的影响

图3(a)为921A钢在不同的弹性拉应力作用下的电极电位随时间的变化曲线。由图3(a)可知，921A钢与电解液接触初期，电极电位迅速负移，而后负移速度减缓，电极电位在金属与腐蚀介质接触后的2 000 s左右基本稳定，稳定的电极电位即为921A钢的腐蚀电位。与无应力试样相比，加载应力试样的腐蚀电位都有不同程度的负移，并且加载的弹性应力越大，腐蚀电位的负移量也越大，当加载的应力为550 MPa时，腐蚀电位的负移量为24.5 mV。这是因为在应力的作用下，晶格中的离子偏离平衡位置，导致金属的电化学活度和表面活性增大，故腐蚀反应所需的活化能减小[7,15]。

考虑到金属腐蚀的力学化学效应，阳极氧化溶解反应的平衡电位由于力学因素的存在而降低[7,10]:

(1)

式中：ΔP为应力张量中水静压部分的绝对值，当承受单轴载荷时，ΔP为所加载单轴应力(σ)的1/3，即ΔP=1/3σ；Vm为金属的摩尔分子体积；z为阳极溶解反应转移的电荷数；F为法拉第常数。根据电化学理论推导可得，由于力学因素引起921A钢腐蚀电位的变化值为[7,22]：

(2)

式中，ba和bc分别为阳极和阴极塔菲尔斜率。由式(1)和式(2)可知，腐蚀电位的变化值与加载的应力之间存在线性关系，921A钢在不同应力下的腐蚀电位如图3(b)所示，腐蚀电位随着弹性拉应力的增大而明显减小，对测量的腐蚀电位进行线性拟合，得到的拟合方程为φcorr=-4.06×10-5σ-0.685，R2为0.979，说明腐蚀电位和外加应力之间具有很强的线性关系，这与上述的理论分析相符。

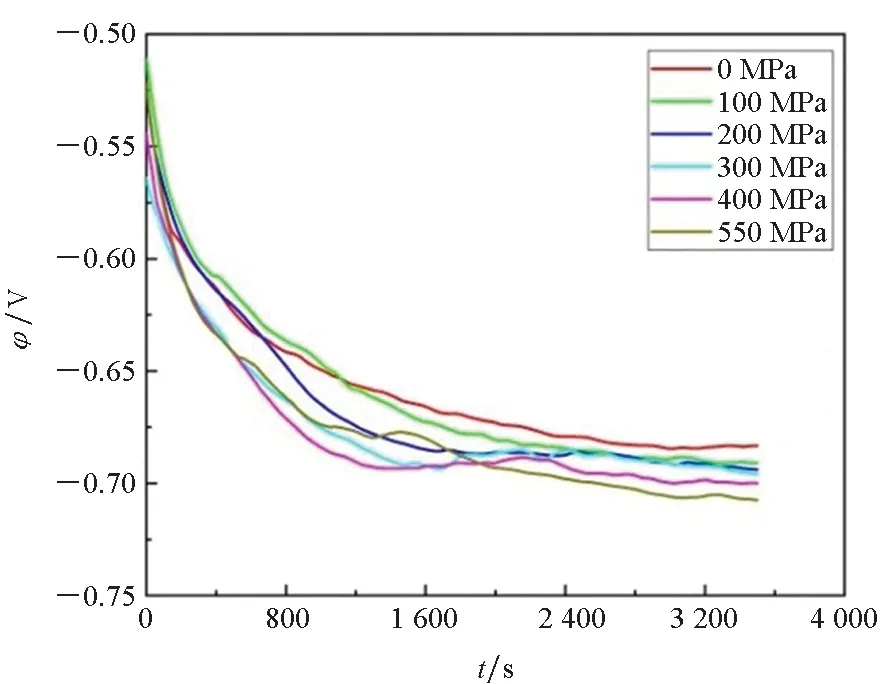
(a) 电极电位(a) Electrode potential

图4为921A钢在加载不同弹性拉应力时的动电位极化曲线。与无应力试样的极化曲线相比，加载应力情况下的极化曲线负移，且应力越大负移也越明显，在同样的阳极极化电位下，阳极电流密度随加载应力的增大而增大，说明弹性拉应力能够加速921A钢的阳极溶解。

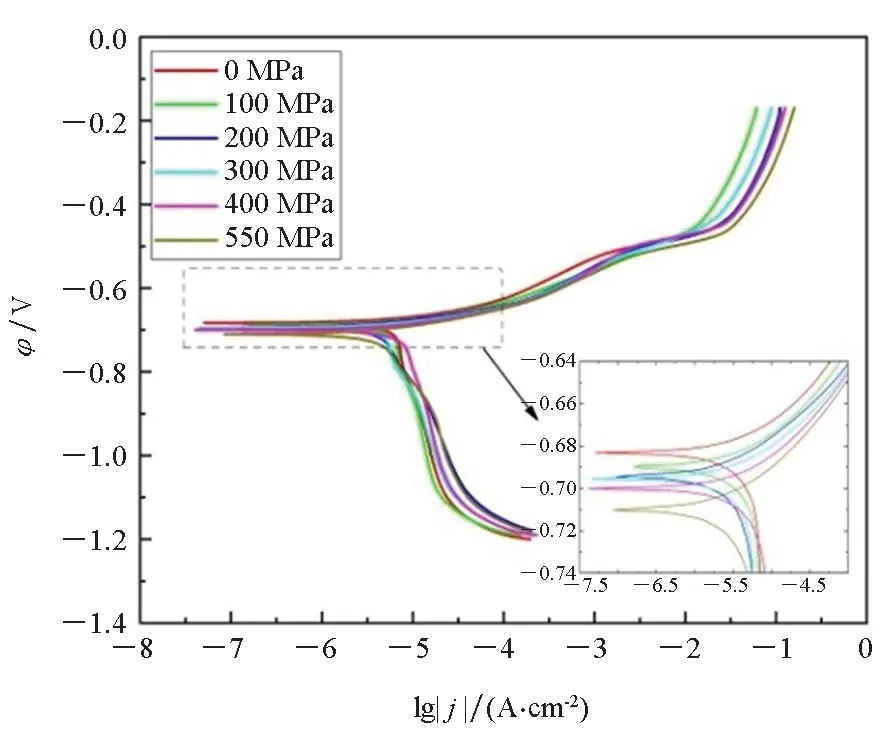
图4 921A钢在不同弹性拉应力下的极化曲线Fig.4 Polarization curves of 921A steel under different elastic tensile stress

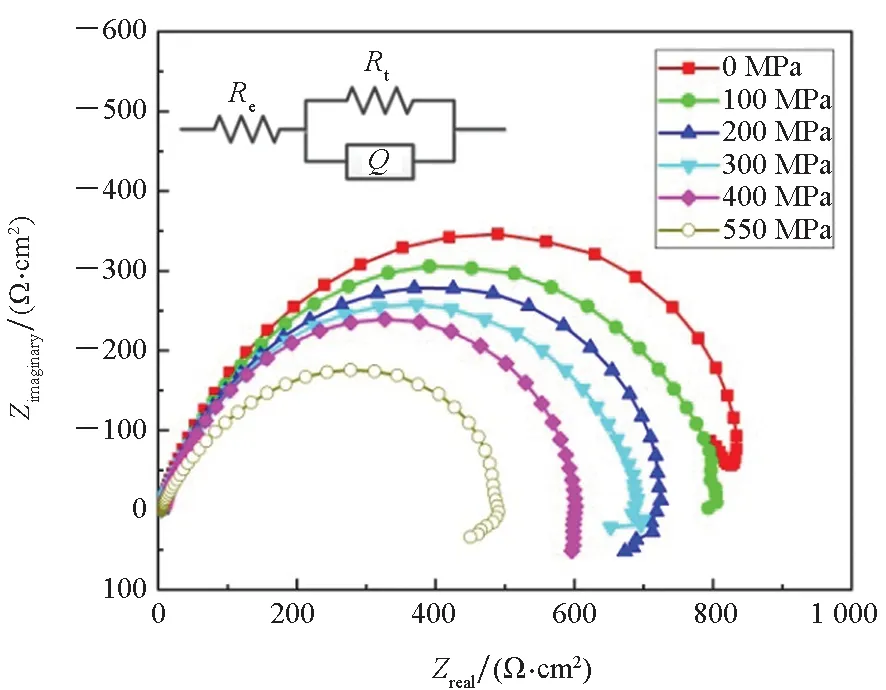
图5(a)为921A钢在不同弹性拉应力作用下的电化学阻抗谱，不同应力作用下的阻抗谱均由一个容抗弧组成，且容抗弧的半径随着弹性拉应力的增大而减小。采用ZView软件对电化学阻抗谱进行拟合，拟合电路为溶液电阻(Re)串联一个常相位角元件(Constant Phase Element, CPE)与电荷传递电阻(Rt)并联的子电路，拟合得到不同弹性应力作用下921A钢腐蚀的电荷传递电阻如表1所示，电荷传递电阻能够反映腐蚀反应进行的难易程度，并与腐蚀速率存在反比关系。Yang等[22]定义了应力作用下的腐蚀速率修正因子f(σ)，其值为应力作用下的腐蚀速率与无应力条件下的腐蚀速率之比，如果用电荷传递电阻来描述应力腐蚀速率修正因子，则[12]：

(3)

图5(b)为921A钢在100 MPa和200 MPa弹性压应力和拉应力作用下的电化学阻抗谱，由图5(b)可知，相同压应力和拉应力作用下的电化学阻抗谱几乎是重合的。由热力学和电化学相关知识可知，金属腐蚀速度与金属电化学势息息相关，电化学势可由Gibbs函数来描述，Gutman[15]从热力学角度理论分析了Gibbs函数在压缩载荷和拉伸载荷下的改变具有对称性，他指出，在应力作用下，固态晶体某一点处局部电化学位的大小，决定于应力张量中水静压部分的绝对值，而与拉伸或压缩固体(相对于作用力为零的平衡状态)的机械作用力的方向无关。电化学阻抗谱测试结果验证了921A钢在相同的拉应力和压应力状态下具有相同的腐蚀速度，Xu等[10]研究了X100管线钢在中性NS4溶液中的应力腐蚀行为，研究结果也说明了X100管线钢在相等的压应力和拉应力作用下具有相同的腐蚀速度。

(a) 拉应力(a) Tensile stress

应力腐蚀速率修正因子与ΔP之间的理论关系如式(4)所示[18]。

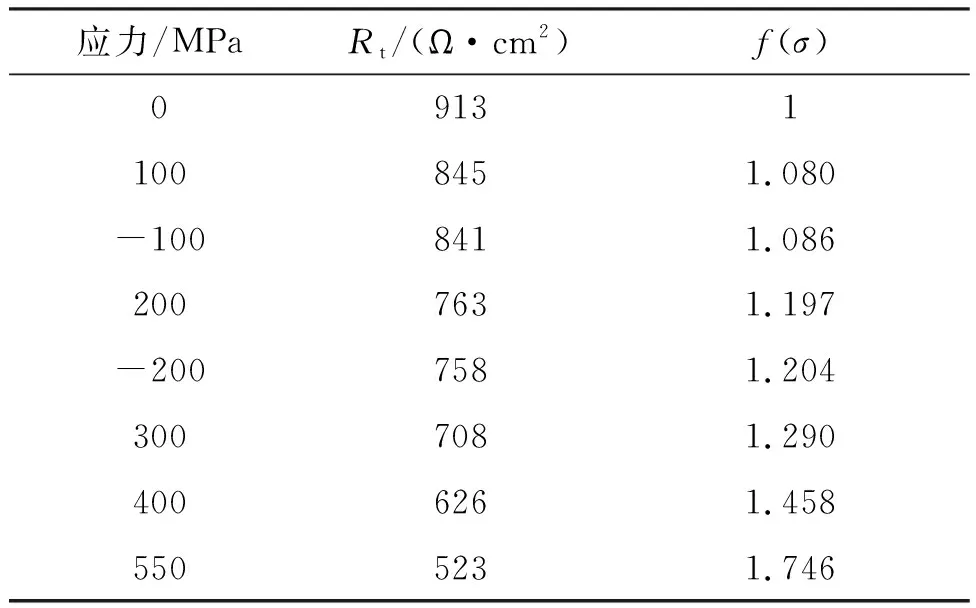
表1 921A钢在不同弹性应力下的电荷传递电阻和腐蚀速率修正因子

(4)

式中，R和T分别为理想气体常数和绝对温度，由于ΔP=1/3σ，因此：

(5)

式中，σ为单轴拉应力或压应力的绝对值。

由式(5)得到的f(σ)与σ之间的理论曲线如图6所示，图中电化学阻抗谱法得到的应力腐蚀速率修正因子为本文的实验结果，失重法得到的应力腐蚀速率修正因子为Gutman[15]对低碳钢的实验结果。由图6可知，本文采用的电化学阻抗谱法能够有效评估921A钢的力学化学效应，在弹性应力范围内，应力腐蚀速率修正因子与外加应力之间存在指数关系。

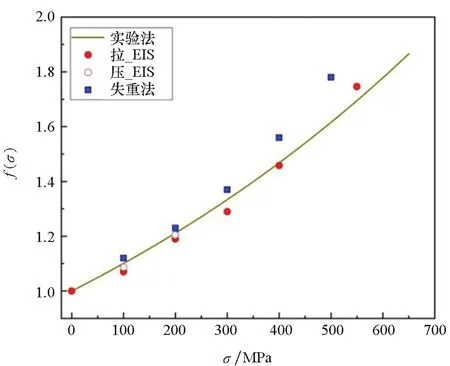
图6 腐蚀速率修正因子随弹性应力的变化Fig.6 Corrosion rate correction factor varies with elastic stress

2.2 弹塑性应变对921A钢腐蚀行为的影响

图7(a)为921A钢在不同弹塑性应变下的电极电位随时间的变化曲线。电极电位在浸泡初期迅速负移，而后逐渐趋于稳定，在本文研究的范围内，弹塑性应变引起的最大腐蚀电位负移量为62.6 mV。图7(b)为921A钢在不同弹塑性应变下的腐蚀电位，由图可知，腐蚀电位随着弹塑性应变的增大先负移而后正移，弹塑性应变为2.6%时，腐蚀电位出现最小值。金属在塑性变形范围内，产生明显的滑移线和位错滑动群，从而引起腐蚀电化学位的增大。

阳极溶解反应自腐蚀电位在塑性阶段的变化值为[11]：

(6)

式中：υ为方向因子；α为系数；N0为塑性变形前的初始位错密度；εp为弹塑性应变。因此，阳极溶解反应平衡电位在弹塑性阶段的总变化值为：

(7)

式中，ΔPm为屈服强度的1/3。

由式(2)和式(7)可知，腐蚀电位与塑性应变之间存在着单调递减关系，而实验结果并不是简单的单调关系。金属在塑性变形的易滑移阶段和形变强化阶段产生新的位错并形成位错平面塞积群，导致力学化学效应急剧增大，而在塑性变形的动态恢复阶段，位错通过横向滑移以及因形成亚晶界和胞状亚结构而部分消失，平面塞积群也因此遭到破坏，从而导致力学化学效应的降低[12,23]。因此，腐蚀电位在弹塑性应变增大到一定程度后出现最小值而后增大，Gutman[15]和Wang等[12]的实验研究结果也证实了这一变化规律。

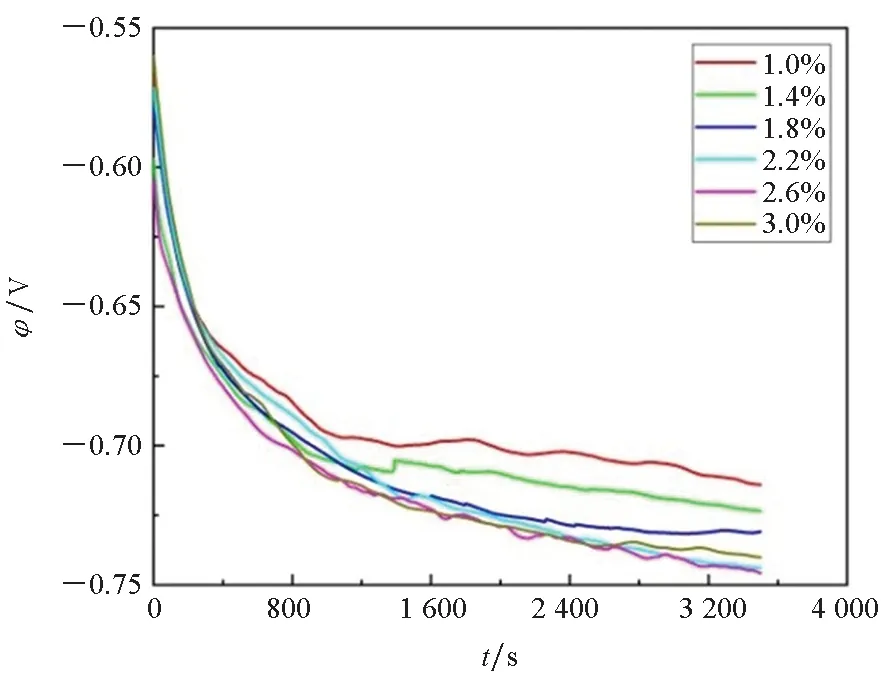
(a) 电极电位(a) Electrode potential

图8(a)为921A钢在不同弹塑性应变下的极化曲线，由图可知，极化曲线随着应变增大而负移的规律与腐蚀电位的变化规律相符。图8(b)为921A钢在不同弹塑性应变下的电化学阻抗谱，由图8(a)可知，弹塑性应变下的阻抗谱由一个高频容抗弧和一个低频感抗弧组成，低频感抗弧可能是由于Cl-吸脱附所引起的[24]。

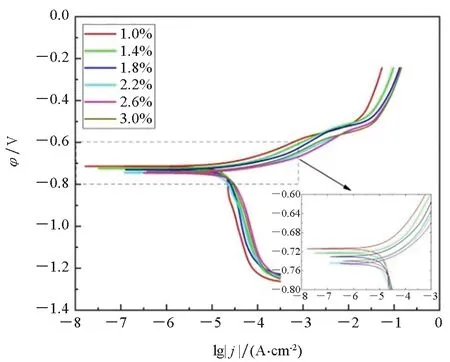
(a) 极化曲线(a) Polarization curves

采用3.2节所述的等效电路拟合阻抗谱的中高频段，拟合得到不同弹塑性应变下的电荷传递电阻如表2所示，表2中的f(σ)为由电荷传递电阻定义的腐蚀速率修正因子。对极化曲线的Tafel区进行拟合，可以得到不同弹塑性应变下的腐蚀电流密度，由腐蚀电流密度定义的腐蚀速率修正因子为：

(8)

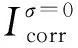
表2 电荷传递电阻和腐蚀电流密度定义的腐蚀速率修正因子

腐蚀速率修正因子与塑性应变εp之间的理论关系为[11]：

(9)

对于低碳钢，υ=0.45，α=1.67×1011cm2，N0=1.0×109cm2，由于921A钢的最大弹性应变为0.4%，因此，腐蚀速率修正因子与弹塑性应变ε之间的关系为：

(10)

由式(10)可以计算腐蚀速率修正因子的理论值，腐蚀速率修正因子随弹塑性应变的变化如图9所示，图中的EIS和Icorr曲线分别为由电化学阻抗谱法和由极化曲线法得到的腐蚀速率修正因子实验值。由图9可知，两种实验方法得到的腐蚀速率修正因子吻合度很高，均随着弹塑性应变的增大先增大后减小，应变为2.6%时出现最大值，这是因为在塑性变形的前两个阶段，新位错和位错塞积群的出现使得力学化学效应急剧增大，而在动态恢复阶段，位错的消失以及平面塞积群的破坏导致力学化学效应反而降低。腐蚀速率修正因子的实验值小于理论值可能是由于拉伸装置螺纹间隙及材料强度等，导致将试样拉伸至指定的变形量后有一定程度的回弹，从而使得实际的弹塑性应变小于设定值。

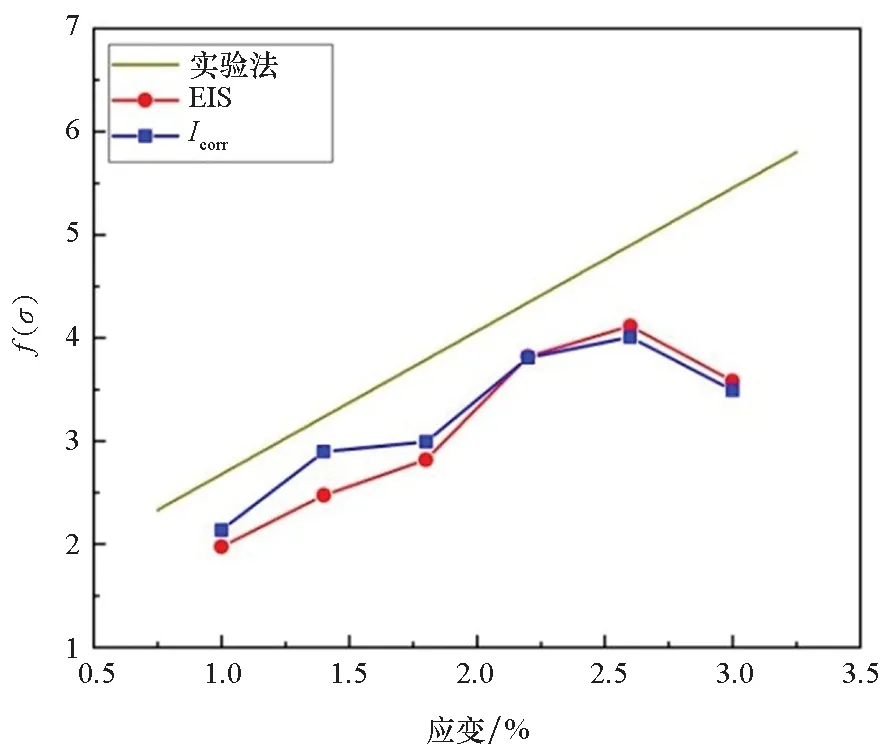
图9 腐蚀速率修正因子随弹塑性应变的变化Fig.9 Corrosion rate correction factor varies with elastoplastic strain

3 结论

1)弹性拉应力与弹性压应力对力学化学效应的影响具有对称性。

2)力学化学效应随着弹性应力的增大而增大，随着弹塑性应变的增大先增大后减小，弹塑性应变对力学化学效应的影响远远大于弹性应力的影响，在本文研究范围内，弹塑性应变引起的腐蚀电位负移量最大为62.6 mV，相应的腐蚀速率修正因子高达4.113，而弹性应力引起的腐蚀电位负移量最大为24.5 mV，相应的腐蚀速率修正因子为1.746，因此应力应变对921A钢在海水中腐蚀行为的影响不容忽视。

3)弹性应力范围内，腐蚀速率修正因子的实验值与理论值吻合度很高，而塑性变形范围内，由于自制的载荷-电化学实验装置不能精确地控制弹塑性应变，导致实验结果小于理论值。