Bang-Bang控制方式旋转导弹气动特性数值分析*

2021-10-10徐一航陈少松

国防科技大学学报 2021年5期

徐一航，陈少松，周航

(南京理工大学能源与动力工程学院，江苏南京 210094)

第二次世界大战以后，精确制导武器在很多条件下取代了无控弹箭，然而精确制导武器的高成本又制约了它的大规模应用，因此一种低成本导弹应运而生。为简化控制系统、降低控制成本，导弹采用旋转的Bang-Bang滚控方式来实现一对鸭舵的单通道控制，通过鸭舵的上下偏转使其在一个周期内为导弹提供一个方向的合力，从而实现导弹的俯仰和偏航运动。

目前，国内外已有很多学者对旋转导弹的气动特性进行了相关研究，王智杰等[1]、刘周等[2]和陈白冰等[3]对高速旋转弹丸的气动力进行数值研究表明，高速旋转弹丸周向压力分布和切应力分布的非对称畸变、边界层的非对称畸变、大攻角下涡的非对称畸变等对马格努斯效应有重要影响。马杰等[4]对高速旋转带有船尾的尖拱圆柱形弹丸进行了数值模拟，结果表明，随着马赫数的增加马格努斯力逐渐减小，马格努斯力与弹丸转速呈线性增大的趋势。Despirito[5]采用雷诺平均和大涡模拟(Reynolds Average Navier-Stockes/Large Eddy Simulation, RANS/LES)混合方法对M910旋转弹丸进行了数值模拟，结果表明全弹的马格努斯力和力矩主要由船尾产生。雷娟棉等[6]研究了船尾外形对旋转弹丸马格努斯效应的影响，总结了马格努斯力及力矩随马赫数、船尾角和船尾长度与弹径的比值的变化规律。船尾产生的侧向力在亚跨声速时随马赫数的增大而增大，在超声速时随马赫数的增大而减小。Yin等[7]、吴放等[8]和张超等[9]对带有尾翼的旋转导弹进行了数值模拟，结果表明尾翼的前缘激波、背风区的分离涡和翼根流动是造成弹体在不同攻角下马格努斯效应出现非线性特征的主要原因，尾翼产生的周期平均侧向力方向与弹身相反，全弹的周期平均侧向力方向在跨音速阶段发生了改变。Yin等[10]研究了带有不控鸭舵的旋转导弹，结果表明鸭舵产生的周期平均侧向力方向与尾翼相同。在亚音速条件下，鸭舵干扰加速了弹体表面边界层的不对称畸变和不同攻角下的流动分离，使平均侧向力绝对值增加。在超音速条件下，由鸭舵引起的激波、膨胀波、涡系和流动分离对侧向力有很大的影响。鸭舵产生的洗流随攻角的增大而改变，这导致尾翼的侧向力先增大后减小。

对于旋转导弹，可以采用成本较低的单通道进行控制，单通道控制常采用如下两种方式：一种方法是加装固定鸭舵的修正组件[11]，如精确导引套件(Precision Guidance Kit, PGK)方式；另一种方法是通过Bang-Bang鸭舵控制方式[12]来实现导弹的俯仰和偏航运动。采用Bang-Bang鸭舵控制的导弹是旋转的，因此会产生马格努斯效应，在旋转过程中鸭舵是不断偏转的，鸭舵的洗流方向会不断发生改变，鸭舵偏转与导弹旋转的耦合会带来更加复杂的流动，进而影响法向和侧向的气动特性。目前国内外对Bang-Bang鸭舵控制方式导弹的气动特性研究相对较少，而Bang-Bang鸭舵偏转带来的气动特性变化更是没见报道，需要进一步明确。

由于导弹旋转、Bang-Bang鸭舵随之偏转是动态的气动过程，通过风洞实验对其研究难度较大。本文采用数值计算的方法，通过CFD软件研究了Bang-Bang鸭舵控制时在不同马赫数、攻角和自旋速度下的气动特性。通过嵌套网格来实现鸭舵的偏转运动，用旋转坐标系方法实现导弹的旋转。当自旋角在0°～90°时鸭舵产生一个斜向上的力，当自旋角在90°～180°时鸭舵转向另一个方向(两者呈现轴对称状态)产生另一个斜向上的力，从而使其在一个周期内产生一个方向的合力，得到导弹飞行控制所需的气动力。

1 数值仿真方法

1.1 几何模型

本文采用国际导弹标模外加两片NACA0012翼型组成的鸭式布局导弹为计算模型，图1展示了该导弹的几何细节。

图1 Bang-Bang滚控导弹几何模型Fig.1 Bang-Bang roll control missile geometric model

该导弹弹径为d=0.045 72 m，全长为L=0.457 2 m，圆锥弹头长径比为2.84倍，弹身是7.16倍弹径的圆柱体，尾翼弦长和展长均为1倍弹径，前缘圆弧半径为0.004倍弹径，后缘厚度为0.08倍弹径，鸭舵半展长为0.5倍弹径，前缘到后缘距离为0.254倍弹径，重心到弹头顶点的距离为5.5倍弹径。选取参考长度Lref=0.457 2 m，参考面积Sref=0.001 64 m2，力矩参考点为质心。

1.2 模拟工况与网格划分

图2中给出了继电控制式鸭舵(即Bang-Bang舵)随导弹旋转而偏转的简图。以一个周期内鸭舵提供一个向上的平均周期力为例，在图2(a)和图2(b)中鸭舵提供一个向左上方的合力，当鸭舵转至垂直位置时，鸭舵偏转换向，在图2(c)和图2(d)中鸭舵提供一个向右上方的合力，与图2(a)、图2(b)中提供的力呈面对称，在一个周期内为鸭舵提供一个向上的合力。

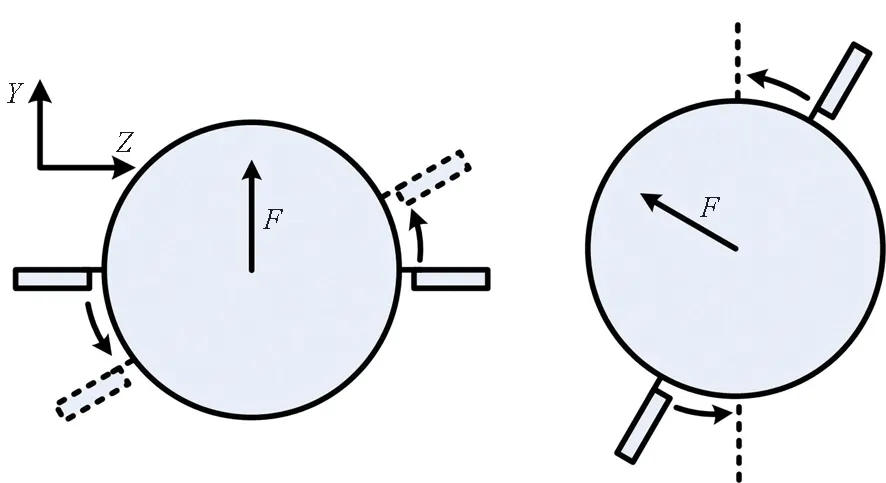
图2 一个周期内模拟工况示意图Fig.2 Simulated working condition in one cycle

在实际过程中鸭舵偏转换向需要时间，而导弹自身在旋转，为保证在铅垂位置的准确换向，需要根据转速设置一个鸭舵偏转换向的提前量，提前量的多少与导弹转速有关。例如：当舵机频率为8.333 Hz、导弹转速为150 r/min时、舵偏角为5°，鸭舵需要在自水平位置起旋转角(简称自旋角)为88.5°时开始偏转，这样才能够保证当自旋角为90°时舵偏角为0°。同理，当导弹转速为600 r/min时，鸭舵则需要在自旋角为84°时开始偏转。这样便能够使自旋角到达96°时的鸭舵与84°时呈现对称状态。

图3展示了三维结构六面体网格，超音速条件下，扰动只能在马赫锥内部顺流传播，上游的流场不受扰动波的影响。为了节约计算资源，超音速远场网格向前延伸1倍弹长，向后延伸10倍弹长，径向约20倍弹径。亚音速条件下，扰动的影响域为全流场。因此，亚音速远场网格向前延伸10倍弹长，向后延伸10倍弹长，径向约20倍弹径。设置第一层网格高度为1.8×10-6以保证y+<1，将网格内边界设置为无滑移绝热壁。导弹的自旋是通过嵌套网格区域的网格运动实现的，嵌套网格技术是将一个背景网格与多个部件网格进行组合，每一套网格单独进行结构化网格划分。在CFD中采用插值法获得背景网格与部件网格中的数据，网格重叠区域采用最小二乘法进行插值，网格重叠的边界处采用三线性插值的方式传递数据。数值计算中，背景网格为亚音速和超音速压力远场，弹体和鸭舵均采用部件网格，外部边界条件设置为Overset。弹体的摆动采用旋转坐标系方法，鸭舵偏转耦合弹体摆动通过用户自定义函数(User Defined Function, UDF)实现，鸭舵打舵偏转时的运动方程为：

其中，ω1为导弹自旋角速度，ω2为鸭舵相对于舵轴的偏转角速度。

坐标系如图3所示，是从弹头向弹尾看去的YZ平面图，X轴由右手定则确定。XY平面是攻角平面。导弹绕着与X轴重合的纵轴旋转，左边的鸭舵序号为1，右边的鸭舵序号为2，两片鸭舵由一个舵机控制，鸭舵的舵偏角大小为5°，并设定控制鸭舵的舵机频率为8.333 Hz。本文定义Cy为法向力系数、Cz为侧向力系数、α为攻角、φ为自旋角、ω为导弹自旋角速度，周期平均侧向力、法向力系数为一个周期内侧向力、法向力系数的平均值。起始时刻，鸭舵与Z轴平行，此时φ=0°。沿X轴负向看，导弹的自旋为逆时针。

(a) 背景网格与弹体的部件网格(a) Background mesh and the part net of the projectile body

本文通过计算Bang-Bang控制式导弹在150 r/min、600 r/min和1 500 r/min转速下、马赫数为0.9、1.2、1.5、2和2.5条件下的气动特性，给出了导弹在一个周期内的法向力和侧向力的气动特性。分析法向力与侧向力的变化规律，并与不控导弹进行对比。

1.3 控制方程和湍流模型

本文采用有限体积法对非定常N-S方程进行求解。采用非定常N-S方程的积分形式作为流体流动的控制方程：

为了提高计算精度与计算效率，本文在计算非定常流动时均采用双时间步法。对于黏度随温度的变化关系，采用萨瑟兰定律，并采用完全气体状态方程。

Yin等[7]和石磊等[13]对带有尾翼的旋转导弹进行了数值模拟，发现S-A、k-ω和k-ε湍流模型的计算结果与阿诺德工程发展中心[14]的实验结果在攻角较小时不能很好地吻合。Nobile等[15]对强风作用下旋转风力机的气动特性进行了数值模拟，将SSTk-ω、k-ω和k-ε湍流模型的计算结果与实验值进行了对比，发现SSTk-ω模型在不利的压力梯度和分离流动中表现良好，本文采用四种湍流模型对ANF旋转标模进行了计算，并将马赫数2.5条件下不同攻角的周期平均侧向力系数与实验结果进行了比较，结果如图4所示，k-ωStandard、k-εStandard和S-A模型在10°攻角时的计算值均与实验值符号相反，SSTk-ω模型虽然也存在误差，但变化规律符合实验值，能够比较好地模拟导弹旋转过程中的马格努斯力。

图4 Ma=2.5时周期平均侧向力系数随攻角的变化Fig.4 Periodic average lateral force coefficient varies with the angle of attack at Ma=2.5

采用三套网格进行网格的无关性验证，分别是390万、620万和910万网格。如表1所示，计算来流马赫数为2.0、攻角为4°。将620万网格的计算结果与390万和910万网格的计算结果相比较，当网格达到620万时与910万网格的侧向力系数仅相差2.54%，为了节省计算资源，超音速条件下本文采用620万网格进行计算。亚音速条件下，按相同网格尺度扩大前场网格，采用970万网格进行计算。

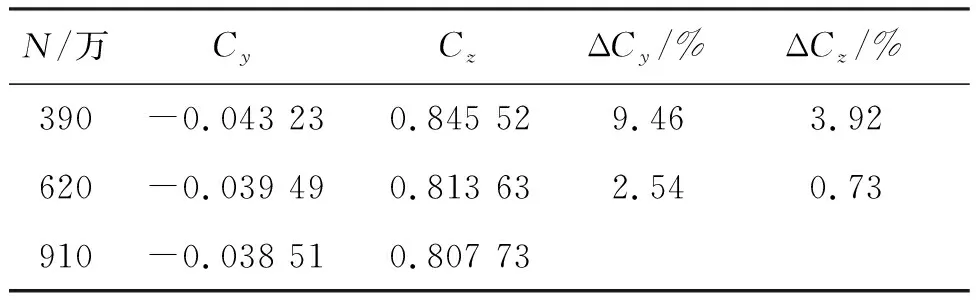
表1 网格收敛性验证

选用三组时间步长进行时间步长无关性验证，分别为ωΔt=0.25°、ωΔt=0.50°和ωΔt=1.00°，即每计算一步弹体旋转0.25°、0.50°和1.00°。图5展示了三种时间步长下的侧向力系数随自旋角的变化曲线。可以看出，随着时间步长的减小，ωΔt=0.25°和ωΔt=0.50°的计算结果相近，而ωΔt=0.50°和ωΔt=1.00°却存在一定差距。由于计算资源有限，选择设置时间步长为ωΔt=0.50°。

1.4 可信度验证

为了验证嵌套网格数值模拟的可信性，采用FM-3导弹的实验结果[16-18]进行验证，局部网格示意图如图6所示。FM-3是一种带有抖动鸭舵的旋转导弹，滚转速率为8.75 Hz，鸭舵的抖动速率为35 Hz、抖动幅度为15°，马赫数为1.6。

图6 FM-3嵌套网格示意图Fig.6 FM-3 overset mesh

图7为FM-3采用嵌套网格方法得到的法向力系数与实验值的对比，采用k-ωSST模型得到的数值模拟结果与实验值吻合较好。由于鸭舵的抖动，这会导致法向力系数的突变，采用数值模拟能够较好地模拟法向力系数的变化。因此，采用嵌套网格方法模拟鸭舵和弹体的耦合运动具有一定的可信度。

图7 FM-3法向力系数Fig.7 FM-3 coefficient of normal force

2 气动特性分析

2.1 侧向力特性

2.1.1 Bang-Bang控制与不偏转鸭舵对比

由于鸭舵的偏转导致洗流在前后半个周期内位于弹体的两侧。这使得全弹的侧向力系数在鸭舵偏转时发生了突变，如图8所示，通过对比不同工况下不偏转鸭舵和Bang-Bang控制式鸭舵全弹的侧向力系数，采用Bang-Bang控制式鸭舵全弹的周期平均侧向力系数更小。图9对比了Bang-Bang控制式鸭舵和不控鸭舵在自旋角为135°时的流场分布图。采用Bang-Bang控制式鸭舵导弹的流线向左偏移得更加严重，这是由于在该状态下，不控鸭舵并未进行偏转，其造成的洗流是向弹体右上方的。而采用Bang-Bang控制式鸭舵由于鸭舵之前进行了偏转，鸭舵的洗流是向弹体左下方的，二者洗流方向不同，导致导弹在后半个周期内的气动特性出现差异。

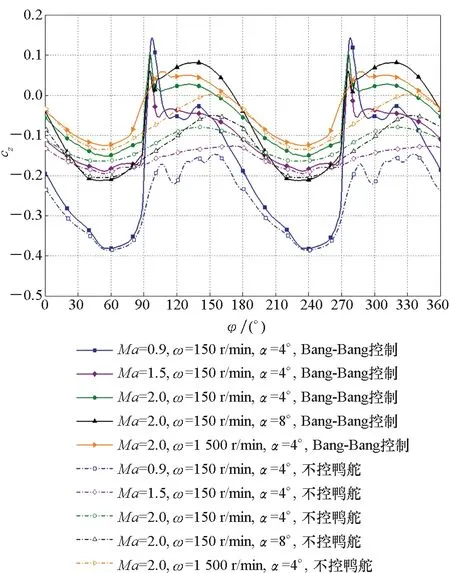
图8 不同工况下侧向力系数变化曲线Fig.8 Variation curves of lateral force coefficient under different working conditions

2.1.2 Bang-Bang控制侧向力特性变化

图10对比了采用Bang-Bang控制式鸭舵和不控鸭舵部件侧向力系数的差异。对于不控鸭舵，鸭舵产生的周期平均侧向力与尾翼产生的周期平均侧向力方向相同。但是当鸭舵进行Bang-Bang控制时，由于鸭舵的偏转导致鸭舵产生的周期平均侧向力减小，鸭舵周期平均侧向力减小的幅度都达到了80%。由于鸭舵的偏转导致洗流方向发生了改变，弹身的侧向力也发生了变化。弹身的周期平均侧向力会减小，周期平均侧向力的方向甚至会发生改变。采用Bang-Bang控制鸭舵也会使尾翼的周期平均侧向力比不控鸭舵的尾翼周期平均侧向力小，因此采用Bang-Bang控制鸭舵全弹的周期平均侧向力要小于不控鸭舵的周期平均侧向力。

图9 Ma=2、α=4°、ω=150 r/min时两种方式导弹周围的流线图Fig.9 Two ways to shoot arrows around the flow chart at Ma=2、α=4°、ω=150 r/min

图10 Ma=2、α=4°、ω=150 r/min时部件周期侧向力系数变化曲线Fig.10 Component periodic lateral force coefficient variation curve at Ma=2、α=4°、ω=150 r/min

图11给出了Bang-Bang控制式导弹在一个周期内三种转速、马赫数为2条件下的侧向力系数变化曲线。随着导弹自旋速率的增加，全弹的周期平均侧向力系数会减小。图12给出了在转速为150 r/min、攻角为4°、不同马赫数下的侧向力系数变化曲线。随着马赫数的减小，周期平均侧向力系数绝对值不断增加，平均侧向力系数绝对值由0.037 64增加至0.186 97。

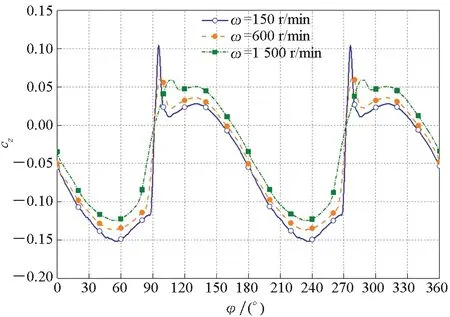
图11 Ma=2时不同导弹转速下周期侧向力系数变化曲线(Bang-Bang控制式导弹)Fig.11 Periodic lateral force coefficient curve of different arrow speeds at Ma=2(Bang-Bang controlled arrows)

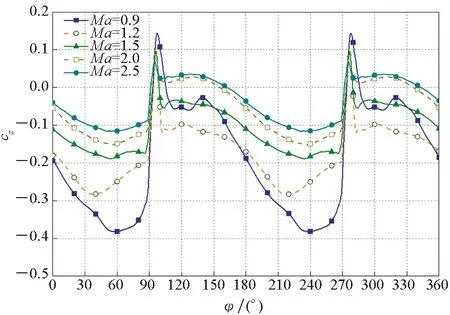
图12 ω=150 r/min、α=4°时不同导弹马赫数下周期侧向力系数变化曲线(Bang-Bang控制式导弹)Fig.12 Periodic lateral force coefficient curve of different arrow speeds at ω=150 r/min、α=4°(Bang-Bang controlled arrows)

2.1.3 侧向力特性变化流场分析

如图13所示，前半个周期内，鸭舵的洗流位于弹体的左上侧(沿x轴负向看去)，而下半个周期内鸭舵的洗流位于弹体的右上侧。对于弹身来说，洗流位置的改变是导致弹身侧向力发生改变的重要原因。尾翼也同样受到鸭舵洗流方向改变的影响，弹身和尾翼侧向力的改变相对于鸭舵来说都表现出一定的滞后性。在图10中可以明显看出，尾翼和弹身侧向力系数的突变都要略滞后于鸭舵，这是由于洗流从鸭舵流经弹体到达尾翼需要一定的时间而产生的现象。

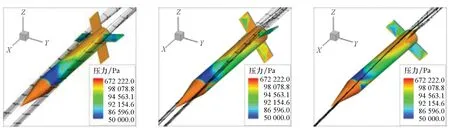
(a) φ=15° (b) φ=35° (c) φ=55°

如图14和图15所示，分别是马赫数为0.9和2、攻角为4°时自旋角分别为45°和135°的弹体周围流线、压力云图以及侧向压强差沿弹轴方向的分布。由于鸭舵产生的侧向压强差较大，为了更好地展示沿弹轴方向侧向压强的分布，将鸭舵的侧向压强差单独提取出来，从侧向压强差分布可以较为直观地展现由于鸭舵的偏转造成洗流方向的改变，在前后半个周期内洗流分别位于弹体的两侧。在鸭舵之后自旋角为45°时出现负压差，当自旋角为135°时由于洗流已经在另一侧，因此出现正压差。超音速条件下，自旋角为45°时在鸭舵之后侧向压强出现负压差，但随着洗流沿弹轴的不断发展，在弹体的后半段侧向压强差由负变正。而自旋角为135°时则没有出现这样的状况。并且鸭舵的洗流在不同位置时对尾翼的侧向压强差也产生了一定影响。亚跨音速条件下，由翼根处诱导出的分离涡对弹体表面的压强分布有很大的影响，分离涡使弹体的侧向压强差出现震荡，但弹身上侧向压强的分布的趋势与超音速大致相同，在弹体的后半段侧向压强差偏向正值。而鸭舵的洗流对尾翼的侧向压强差并未产生太大的干扰。

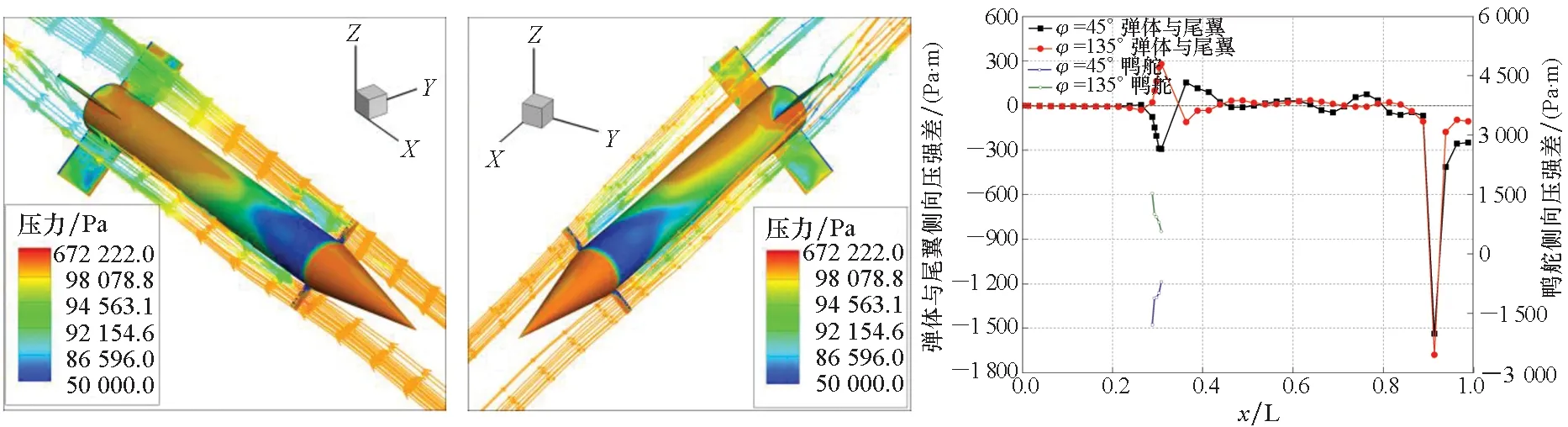
(a) φ=45° (b) φ=135° (c) 侧向压强差(c) Lateral pressure difference图14 Ma=0.9、α=4°时鸭舵洗流流线图和侧向压强差沿弹轴分布曲线(Bang-Bang控制式导弹)Fig.14 Flow diagrams of the canard flowing and distribution curve of lateral pressure difference along missile axis when Ma=0.9、α=4°(Bang-Bang controlled arrows

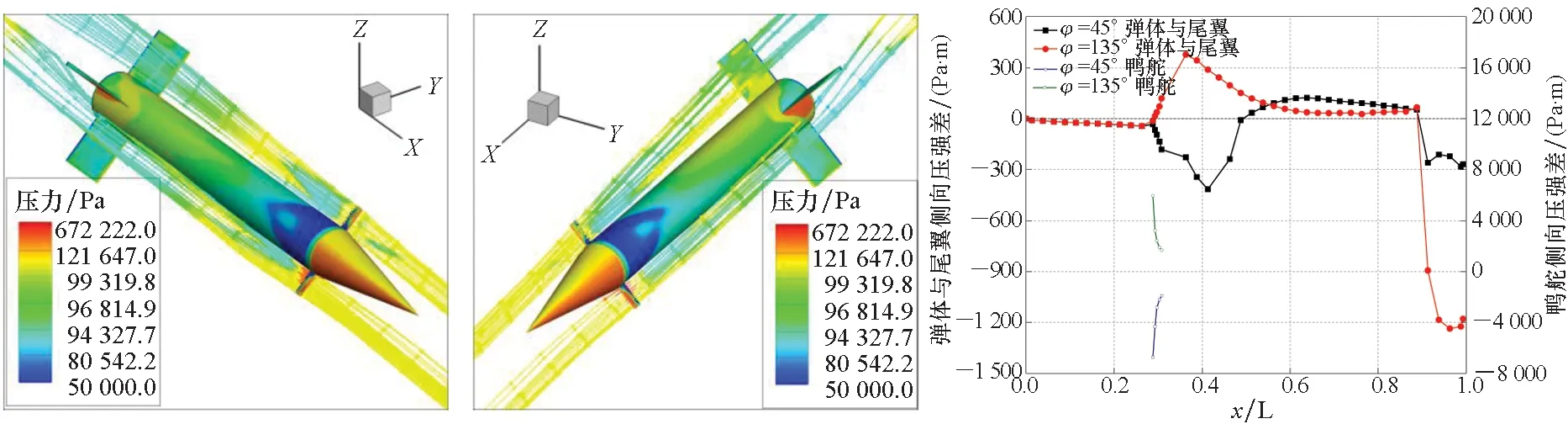
(a) φ=45° (b) φ=135° (c) 侧向压强差(c) Lateral pressure difference图15 Ma=2.0、α=4°时鸭舵洗流流线图和侧向压强差沿弹轴分布曲线(Bang-Bang控制式导弹)Fig.15 Flow diagrams of the canard flowing and distribution curve of lateral pressure difference along missile axis when Ma=2.0、α=4°(Bang-Bang controlled arrows)

通过观察图16导弹不同位置横截面上压力云图和流线分布可以发现，当鸭舵的洗流位于弹体左侧时，洗流产生的涡流会充分发展，涡流破坏了弹体左侧表面的压强分布，使左侧弹体表面的压强增加，从而使侧向压强差由负变正。并且涡流会延伸到尾翼的左侧和上侧之间，这极大地引起了尾翼之间流动的不对称性。

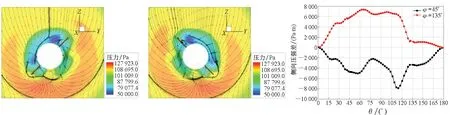
(a) φ=45° (b) φ=135° (c) x/L=0.4

当鸭舵的洗流位于弹体右侧时，鸭舵产生的涡流并未充分发展，这一点在亚音速表现得更为明显。这是因为位于右下侧鸭舵产生的涡流为逆时针方向，而弹体的旋转方向也为逆时针，这就极大地削弱了涡流的发展。而位于左上侧的鸭舵产生的涡流随着流动不断远离弹体，从而使侧向力为正。由于鸭舵洗流方向的改变，以及洗流和弹体旋转的耦合效应，导致导弹会产生侧向力，并且呈现周期变化。通过对一个周期内导弹的法向力系数和侧向力系数进行积分，可以得到一个周期内导弹合力的方向。

由于侧向力的存在，导致导弹在一个周期内的合力并不是沿Z轴正方向的。如表2～4所示，表中的角度表示合力方向与Y轴正方向的角度，取逆时针方向为正。从表中偏离的角度可以看出，随着马赫数的增加，合力偏离Z轴的角度逐渐减小，在相同马赫数下该角度也随着转速的增加而减小。这是由于在亚音速条件下鸭舵的干扰加速了弹体表面的非对称畸变和流动分离[10]，因鸭舵根部诱导出的分离涡方向的改变对周期平均侧向力起主导作用。超音速条件下由鸭舵引起的激波、膨胀波是侧向力产生的主要原因[10]，因此在超音速条件下弹体以及尾翼产生的周期平均侧向力较小，并且随着马赫数的增大而减小。合力偏离Z轴的角度也随攻角的增大而减小，这是因为随着攻角的增大，法向力也逐渐增大，侧向力相对于法向力来说变得越来越小。攻角增大，鸭舵诱导出的洗流离开弹体的速度加快，由鸭舵诱导的涡旋对弹体和尾翼产生的影响减小。

表2 α=4°时全弹合力方向与Z轴的夹角

表3 Ma=2时全弹合力方向与Z轴的夹角

表4 ω=1 500 r/min时全弹合力方向与Z轴的夹角

2.2 法向力特性

2.2.1 Bang-Bang控制与不偏转鸭舵对比

当鸭舵进行Bang-Bang控制时，由于旋转效应，会导致全弹以及各个部件的法向力呈现周期性变化，全弹的法向力可以通过计算一个周期内的时均法向力得到。但由于鸭舵的偏转导致洗流方向发生变化，鸭舵的洗流在前后半个周期内分别位于弹体的两侧，这使得采用Bang-Bang鸭舵控制的自由旋转导弹的气动特性与鸭舵没有偏转的自由旋转导弹的气动特性有所不同。图17是几个不同工况下鸭舵进行Bang-Bang控制和不控鸭舵法向力系数的对比。由于采用Bang-Bang控制导弹的鸭舵进行了偏转，因此其法向力周期与不控鸭舵相同。但由于Bang-Bang鸭舵具有舵偏角，因此其法向力要大于不控鸭舵。

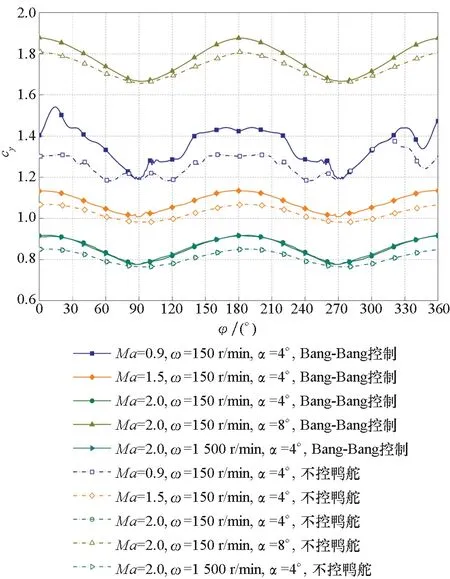
图17 不同工况下法向力系数变化曲线Fig.17 Change curve of normal force coefficient under different working conditions

2.2.2 Bang-Bang控制法向力特性变化

图18给出了在转速为150 r/min、不同马赫数下的法向力系数变化曲线。自旋角为0°时鸭舵位于水平方向，此时产生的法向力最大。随着自旋角的增加，鸭舵贡献的法向力逐渐减小，在自旋角为90°时达到最小值。通过对比图18和图19，法向力系数随马赫数的增大而减小、随攻角的增大而增大，这符合导弹的气动力规律。自旋速度对超音速条件下的法向力系数影响较小。

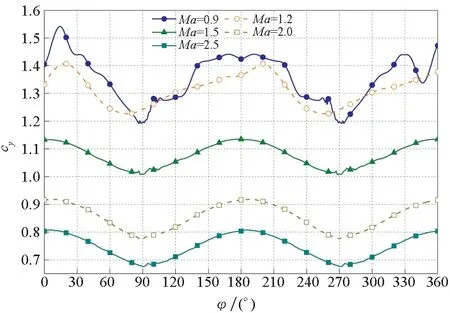
图18 ω=150 r/min时不同导弹马赫数下周期法向力系数变化曲线(Bang-Bang控制式导弹)Fig.18 Periodic normal force coefficient curve at ω=150 r/min(Bang-Bang controlled arrows)

图19给出了一个周期内弹身和尾翼的法向力系数变化曲线，可以看出，在一个周期内弹身的法向力系数先减小后增大，而尾翼的法向力系数却是先增大后减小，造成这种现象的原因便是因鸭舵偏转导致的洗流方向的改变。

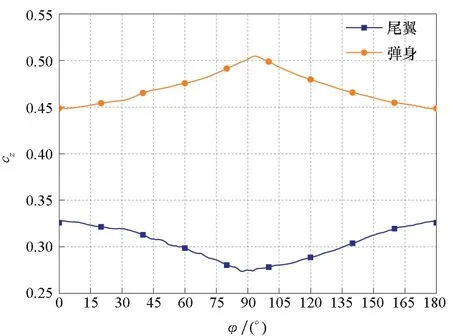
图19 Ma=2、α=4°时周期法向力系数变化曲线(Bang-Bang控制式导弹)Fig.19 Periodic normal force coefficient curve at Ma=2,α=4°(Bang-Bang controlled arrows)

2.2.3 法向力特性变化流场分析

图20展示了前半个旋转周期中翼根处拖出的洗流沿弹表面的流动过程。由于导弹的旋转，从左边鸭舵根处产生的洗流逐渐向尾翼靠拢，洗流先流至尾翼下表面。随着尾翼的继续旋转，洗流被尾翼分离，一部分从尾翼的上表面流过。

(a) φ=25° (b) φ=45°

由于鸭舵的洗流作用以及导弹的旋转效应，导致尾翼的当地攻角增加，从而使尾翼的下表面高压区增大，图21中的尾翼下表面压力云图就给出了很好的解释(尾翼上、下表面的界定由尾翼的当地攻角来确定，即当地攻角为正值时的迎风面为下表面，当地攻角为负值时的迎风面为上表面)。四个子图分别是尾翼在自旋角为45°和75°以及导弹在下半个周期内在相同位置处时(即自旋角为135°和165°)的尾翼下表面压力云图。可以看出，洗流会使下表面的高压区增多，从而使该片尾翼的法向力增大。

(c) φ=75° (d) φ=165°图21 Ma=2.0时尾翼处压力云图(Bang-Bang控制式导弹)Fig.21 Pressure cloud at the tail when Ma=2.0(Bang-Bang controlled arrows)

图22是自旋角为15°、45°和75°时鸭舵洗流下的尾翼下表面压力云图。初始时洗流并未流到尾翼下表面，因此下表面并未产生高压区。但是随着尾翼当地攻角的增加，以及鸭舵的洗流对尾翼下表面的影响，尾翼下表面的高压区不断增加。随着自旋角的增加，该尾翼逐渐由竖直变为水平，对法向力的贡献逐渐增加，从而使法向力逐渐增加。后半个周期中，由于鸭舵的偏转导致洗流流向弹体的另一侧，此时鸭舵的洗流便对另外一侧的尾翼产生了影响，这个过程刚好与上半个周期相反，因此尾翼的法向力在一个周期内先增大后减小。