线性液动压抛光流场的剪切特性研究

2021-10-09文东辉许鑫祺郑子军

中国机械工程 2021年18期

文东辉许鑫祺郑子军

浙江工业大学机械工程学院，杭州，310023

0 引言

近年来，超光滑表面加工是微电子、光学领域的研究热点，随着机理认识的深入、表面检测技术的进步，超光滑表面抛光技术也不断更新[1]。流体动压抛光作为一种典型的非接触抛光，在抛光过程中抛光工具与工件处于非接触状态，借助流体动压效应配合抛光液来实现材料的原子级别去除，具有表面及亚表面损伤小、晶体结构完整、残余应力低等优点[2]。

国内外学者在此基础上提出了各类衍生抛光技术。YOSHIHARU等[3]开发了浮法抛光，用其加工高纯度单晶氟化钙，Nomarski干涉差显微镜和扫描隧道显微镜测试结果显示其具备加工超光滑表面能力。KUBOTA等[4]首先提出了弹性发射加工，并借其实现了用于X射线聚焦的反射镜的曲面抛光，表面粗糙度均方根(RMS)从0.3 nm降至0.16 nm。WATANABE等[5]在动压推力轴承的基础上研发了动压浮离抛光。WEN等[6]设计了带有楔形结构与约束边界的抛光盘，1500 r/min抛光盘转速、50 μm抛光间隙下，采用50 nm的SiO2磨料可在2 h内将纯铜工件的粗糙度Ra从15 nm降至3.5 nm左右，根据纳米压痕观测结果，抛光后损伤层深度小于100 nm。郑子军等[7]研究了不同抛光盘微结构参数下的动压分布，通过优化设计改善了工件区域动压特性。

对流体动压抛光而言，流体剪切力与材料去除机理息息相关。KUBOTA等[8]研究得出，流体润滑动压膜的剪切应力越大，弹性发射加工(elastic emission machining,EEM)对工件的去除率就越高。李庆宇[9]通过表层原子结合键能推导了实现材料去除的最小剪切力方程式，据此获得了转速与抛光间隙的初步合适取值范围；弥谦等[10]以非牛顿流体为抛光液，通过剪切增稠效应来增大剪切应力，从而提高材料去除率。已有研究主要集中在剪切力与材料去除的定性联系，未见对流场剪切特性的深入研究，包括剪切力分布的规律探究与相关预测评价。

本文以线性液动压抛光(linear hydrodynamic polishing，LHP)为研究对象，研究其流场剪切力分布，建立了剪切特性预测模型。

1 线性液动压抛光理论分析计算

1.1 线性液动压抛光原理

LHP原理见图1，包括抛光工具、加工环境、工件三部分。抛光工具为带有若干个周向微结构的圆柱形抛光辊子，以一定深度浸没于充满抛光液的抛光槽中，周向微结构在抛光中可形成压力回流区域，提高抛光效果[11]；工件位于抛光辊子的正下方，抛光间隙极小；工件架定位夹紧工件的同时能带动工件往复运动，实现全表面抛光。

图1 LHP抛光原理

根据动压润滑理论，高速旋转的抛光辊子带动抛光液进入微米级抛光间隙，形成动压液膜，液膜区域内，垂直于工件的动压力场与平行于工件的剪切力场驱使抛光液以一定速度和角度冲击工件表面，实现表面原子的去除。

1.2 流场剪切力数学模型

本文重点研究LHP动压液膜内剪切特性，根据抛光特点和雷诺方程等来推导动压液膜内剪切力分布方程。

1.2.1雷诺方程简化

流体动压润滑是指黏性流体通过具有适当几何形状的两摩擦表面形成一定厚度的润滑液膜，可通过液膜动压来平衡外载荷。在抛光加工中运用液膜动压和液膜剪切实现材料去除。它的形成需要三个基础条件：收敛间隙、黏性流体、相对滑动。

假设雷诺方程普遍形式如下：

(1)

式中，u、v、w分别为对应的x、y、z方向速度分量；ρ为流体密度；h为动压液膜膜厚；p为流体动压力；μ为流体动力黏度。

图2为LHP动压润滑区域示意图。根据LHP加工特点，抛光液可视为牛顿流体，无y向相对速度，无膜厚挤压效应[12]。式(1)可简化为

图2 LHP动压润滑区域示意图

(2)

引入边界条件：h=h0，∂p/∂x=0，h0为最小膜厚(即抛光间隙)，即可得到LHP动压液膜内压力分布：

(3)

1.2.2剪切力方程推导

流体运动时，上下流层之间由于流体黏性会存在速度分层，这种不同速度流层之间的相互作用力就是流体剪切力。根据牛顿内摩擦定律，牛顿流体剪切力定义如下：

(4)

式中，du/dz为流体速度梯度；剪切力τ始终为正。

纳维-斯托克斯方程的含义是：微元体内动量的时间变化率等于作用在微元上的外力之和，其x向微分形式如下：

(5)

其中，Fx为单位质量流体微元受到的质量力。等号左边表示惯性力作用效应，右边第一项为体积力作用效应。

根据动压润滑理论推导基本假设[13]，即忽略体积力、惯性力，忽略膜厚方向压力变化，du/dz远大于du/dx、du/dy，式(5)可简化为

(6)

等式两边对z二次积分，可得

(7)

式中，c1、c2为常系数。

引入边界条件：工件面静止，即z=0，u=0；辊子面转动，即z=h，u=u0，u0为辊子线速度。可得动压润滑区域流体速度

(8)

结合式(4)可得到动压液膜剪切力

(9)

联立式(3)和式(9)，取z= 0，即可得到LHP流场底部(工件面)剪切力分布解析式：

(10)

2 剪切力数值模拟

剪切力理论解析式的推导需要建立在假设简化之上，而原始的雷诺方程求解过于复杂，故采用计算流体动力学(CFD)近似求解LHP流场剪切力分布。

2.1 有限元模型与求解策略

采用GAMBIT软件建立LHP的流场模型，如图3所示，整体流场尺寸为260mm×(240+h0)mm×90 mm，h0取20 μm、40 μm、60 μm，抛光辊子位于流场底部正上方，厚度为30 mm，工件位于流场底面抛光辊子正下方。为保证数值模拟结果的收敛性与准确性，对流场模型进行结构化网格分块划分，对间隙内动压液膜区进行网格加密，x、y向采取对称划分。划分后模型网格单元数为1 753 026、网格面数为5 336 630、网格节点数为1 830 154。

图3 LHP流场模型

采用FLUENT软件对LHP动压液膜区域剪切力进行仿真分析。FLUENT中描述两相流的模型有三种，分别为Mixture、Eulerian、VOF。LHP抛光液为混合固液两相，选用的Eulerian模型有更好的精度与界面特性。通过计算，间隙流场雷诺数小于4000，故选用Laminar层流模型。对模型辊子外表面采用动壁面转速设置，流场上表面与大气相连，采用压力出口设置，相对压为0，并以上表面为基础创建抛光液与大气分割面，上层设置空气相，下层设置固液混合相。

2.2 数值模拟结果分析

如图4所示，LHP剪切力主要集中在抛光辊子与流场底面工件的间隙内，即抛光过程中在工件表面形成的动压润滑区域内。

图4 流场剪切力整体分布情况

为了更好地表述剪切力变化趋势，利用后处理软件对流场底面云图进行适当调整，图5、图6为转速2000 r/min、间隙40 μm、黏度0.025 Pa·s下的流场底面剪切力3D和2D分布云图。

图5 流场底面3D分布云图

图6 流场底面2D剪切云图

从图6中可以看出剪切力呈细长带状分布，整体呈由中心向两侧对称递减趋势，但沿x、y方向的剪切力变化趋势不尽相同，因此以分布中心为原点，分别提取x=0下的y向、y=0下的x向数据点绘制曲线，如图7、图8所示。

图7 y向剪切分布

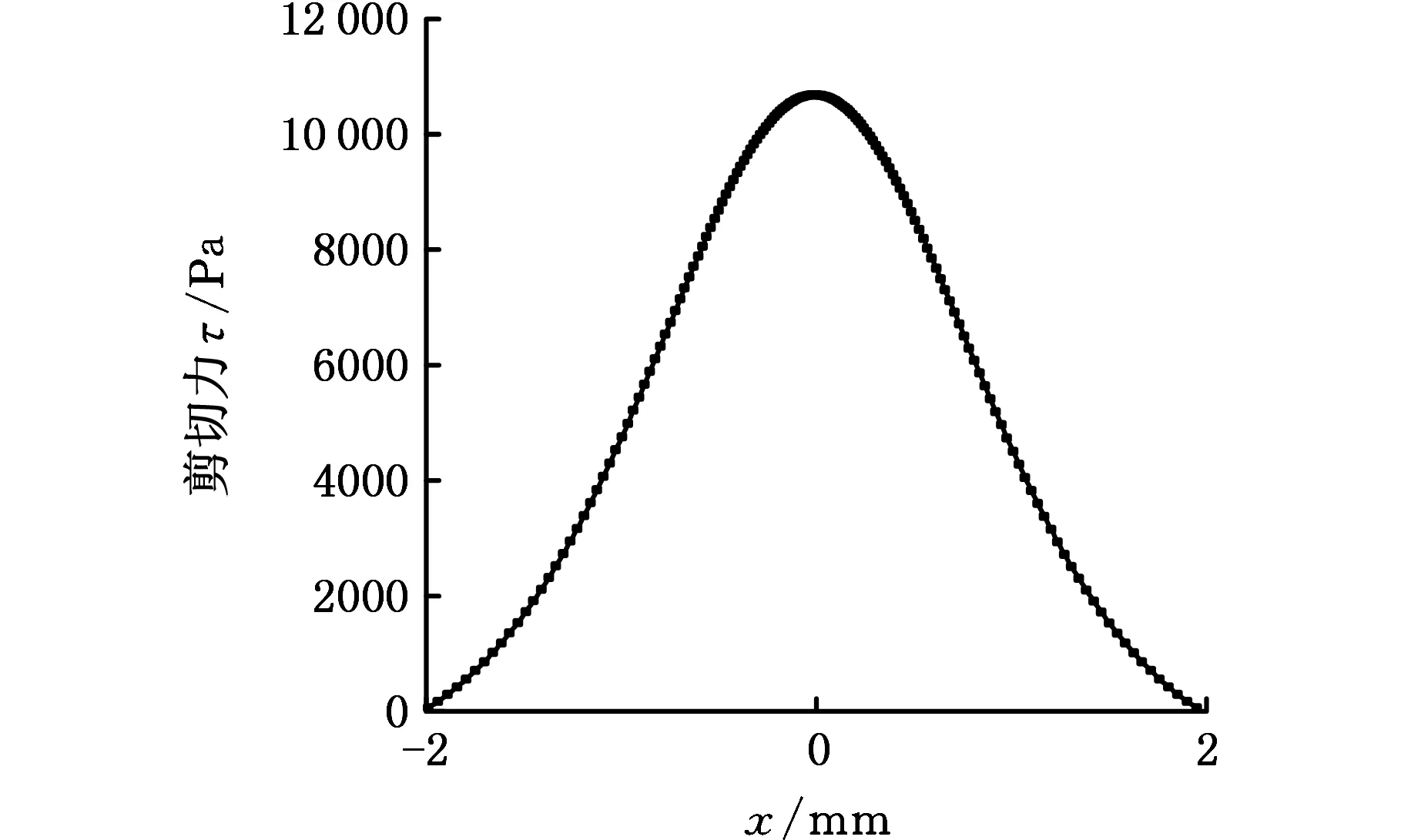
图8 x向剪切分布

以图7中y向分布来看，在辊子厚度30 mm范围内，除两端泄压，剪切力有急速下降外，其余剪切力分布均匀，常用工件尺寸为15 mm×15 mm，能完全均匀覆盖工件面。以图8中x向分布来看，剪切带宽较为狭窄，不足2 mm，且如图1所示x向为进给方向，瞬时剪切分布将叠加作用于工件表面x向，因此需重点对x向剪切分布进行研究。

2.3 流场剪切力灵敏度分析

根据剪切力理论推导可知剪切力分布与速度u、抛光间隙h0、抛光黏度μ直接相关，其中u与辊子半径r、辊子转速n相关，为探究各参数对LHP流场x向剪切力分布的影响规律及显著程度，采用控制变量法分别建立流场模型进行仿真计算，参数如表1所示。

表1 各参数取值水平

当h0=40 μm、μ=0.025 Pa·s、r=75 mm，

转速分别取1000 r/min、2000 r/min、3000 r/min时，得到不同转速下的x向剪切力分布，如图9所示。由图9可知，抛光辊子转速的改变基本不会对剪切力带宽产生影响，即动压液膜区域宽度不变；随着抛光转速的增大，间隙上表面线速度u也随之增大，剪切力线性增大。

图9 不同转速下的剪切力分布

当n=2000 r/min、h0=40 μm、r=75 mm，黏度分别选取0.015 Pa·s、0.025 Pa·s、0.035 Pa·s时，得到不同黏度下的剪切力分布如图10所示。由图10可知，抛光液黏度的变化同样不会改变剪切力带宽度；随着黏度的增大，流体剪切力呈线性上升趋势。

图10 不同黏度下的剪切力分布

当n=2000 r/min、μ=0.025 Pa·s、r=75 mm，间隙分别选取20 μm、40 μm、60 μm时，得到不同间隙下的剪切力分布如图11所示。由图11可知，随着抛光间隙的增大，流体剪切力反而减小；越小的间隙下的剪切力分布越集中，宽度越小。

图11 不同间隙下的剪切力分布

n=2000 r/min、μ=0.025 Pa·s、h0=40 μm，辊子半径分别选取50 mm、75 mm、100 mm，得到不同半径下的剪切力分布，如图12所示。由图12可知，随着抛光半径的增大，间隙上表面线速度u增大，剪切力随之增大，剪切力带宽也随之增大。

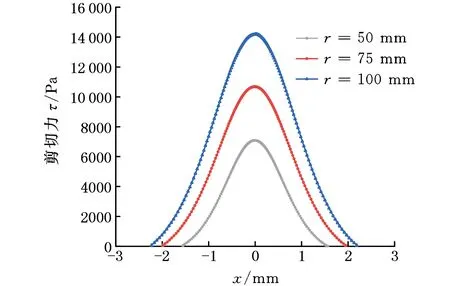
图12 不同辊子半径下的剪切力分布

根据上述剪切力分布对比发现各参数对剪切力的影响不尽相同，主要体现在剪切力带宽和剪切力峰值的差异上。由2.2节分析可得，x向瞬时剪切分布相对y向较窄，未能均匀覆盖到工件面。LHP加工x向引入连续进给运动，使得瞬时的剪切分布叠加作用于工件表面，因此在不考虑其他干扰因素的情况下，瞬时剪切力分布越“陡峭”(即有效剪切去除集中在最小间隙h0处)，对其他区域影响越小，整体剪切去除效果也越好。

综上所述，为能数学量化表述剪切特性，引入评价指标k：

式中，τmax为剪切力峰值；m为剪切力单侧带宽。

为能直观对比各参数对剪切特性的影响程度，引入相对灵敏度函数：

(11)

式中，xi代表n、μ、h0、r；k(xi)为以各参数为自变量的剪切特性评价指标。

相对灵敏度计算结果见表2。可以看出，S(h0)>S(μ)>S(n)>S(r)，因此LHP流场剪切特性对抛光间隙最为敏感，其次是辊子黏度与抛光液转速，最不敏感的是抛光辊子半径。若考虑到数值计算的误差，辊子转速与抛光液黏度敏感度应在同一水平。

表2 相对灵敏度计算结果

根据简化推导的剪切力理论解析式(10)，流场x向剪切力峰值τmax(∂p/∂x=0)与n、r、μ成正比，与h0成反比；剪切力带宽m(τ=0)仅与r、h0正相关，与各参数影响规律、灵敏度分析结果一致。

3 基于支持向量回归的剪切特性预测模型

建立基于支持向量回归(SVR)的预测模型，以便准确预测给定实验参数组合下的剪切特性。

3.1 试验设计

根据灵敏度分析结果，剔除相对不显著参数r，选取抛光辊子转速n、抛光间隙h0、抛光液黏度μ作为试验设计因素，每个因素取5水平，如表3所示。

表3 因素水平表

以剪切特性评价指标k作为响应，3因素5水平正交试验设计和结果见表4，按照表中25个试验组建立流场模型进行仿真计算。

表4 正交试验设计和结果

3.2 预测模型的构建

支持向量回归是在支持向量机(SVM)基础上引入不敏感损失函数ε构筑而成。相比于其他机器学习技术，如传统神经网络，SVR具有所需试验样本小、全局最优、泛化能力强等优点[14]。

利用SVR建立剪切特性预测模型，旨在寻找一个最优分类面使得各训练样本与之总偏差最小。通常的流程为将低维数据映射到高维空间，在高维空间得到最优超平面进行线性回归，从而得到在原空间进行非线性回归的效果[15]。

将25组试验设计因素及指标作为SVR训练集{xi,yi}，i=1,2,…,25，其中xi为试验因子，yi表示LHP剪切特性评价参数k。

定义高维空间线性回归函数：

f(x)=wφ(x)+b

(12)

式中，φ(x)为非线性映射函数；w为垂直于对应超平面的法向量；w，b联合定义超平面。

(13)

引入Lagrange乘子α、β，将式(13)转换为对偶形式，约束条件如下：

(14)

其中，K(xi,xj)为用于简化非线性逼近的核函数，K(xi,xj)=φ(xi)φ(xj)，从而避免计算非线性映射φ(x)，不增加计算复杂性。

求解式(14)，即可得到

(15)

将式(15)代入式(12)即可得到剪切特性评价指标k的预测模型函数：

(16)

3.3 预测模型的程序实现

基于上述预测模型的数学描述，借助MATLAB软件实现LHP剪切特性的预测模型构建，流程如图13所示，图中g为核因子。

图13 SVR预测模型实现流程图

以表4中25组试验数据为基础随机产生训练集，对所有输入样本做归一化处理，使得不同维度的数据都处在[0,1]范围内，从而提高模型的训练速度和精度；惩罚因子C与核因子g是决定模型性能的关键参数，C值越大，模型允许误差越小，但会降低模型泛化能力；g值大小与试验数据输入范围成正相关。本研究选用径向基核函数(RBF)作为模型核函数，交叉验证寻找确定了最佳C=1024和g=0.011，并据此建立训练预测模型。

对建立的预测模型进行仿真测试，比较模型预测值与真实值，并通过计算均方误差(MSE)、回归相关系数(R2)评价SVR预测模型的优劣，如图14所示。

图14 SVR预测模型评价图

由于k值跨度较大，样本点主要集中在预测直线的尾部，少量分布于直线中上区，大部分试验样本点都落在预测直线周围。R2代表整个回归模型的拟合程度，一般要求大于0.85，越接近1，拟合程度越高,SVR模型R2为0.983 52，训练集均方误差为0.003 443 7，模型拟合程度良好。综上所述，LHP剪切特性的SVR预测模型基本可靠。