变电站电气设备主接线故障在线诊断方法研究
2021-10-09宋景博张金凤闫向阳
李 凯,宋景博,张金凤,闫向阳,赵 冲
(国网河南省电力公司经济技术研究院,河南 郑州 450000)
0 引言
电力系统的安全、稳定运行取决于电力设备主接线的可靠度。变电站内的电力设备包括变压器、断路器、母线和隔离开关等[1]。随着电力容量的增大,电气装置结构日益复杂,元件的数量也相应增多。国际上,电气主接线可靠性研究始于20世纪70年代,主要研究断路器的3状态模式[2]。在20世纪90年代,比林顿推出了广域n+2状态马尔科夫模式[3],并将其应用于发电站的可靠算法评价。后来,国内学者利用解析法诊断变电站主接线故障。解析法采用的具体方式较多,在实现过程中主要有状态空间法、故障后果评价法、故障树分析法和最小割集法[4]。目前,电气设备主接线故障的诊断在电力设备的可靠性监测中是十分重要的,许多研究方法尚处于起步阶段。因此,建立一套完善的电气设备主接线故障在线诊断方法已经成为当下迫切需要解决的问题。
1 电气主接线元件传统模型
1.1 断路器模型
电气设备的断路器是主要操作部分,结构复杂。其功能一般包括切除短路电流、倒闸操作等[5]。基于多种因素,断路器的可靠性模型通常包含7种状态。最常见的是正常运行状态N、计划修复状态M、强迫修复状态m、误动状态f。在上述状态之外,一般还包括接地或绝缘故障状态i、拒动状态St和故障后修复状态r。这些状态共同组成了断路器的7状态空间,如图1所示。
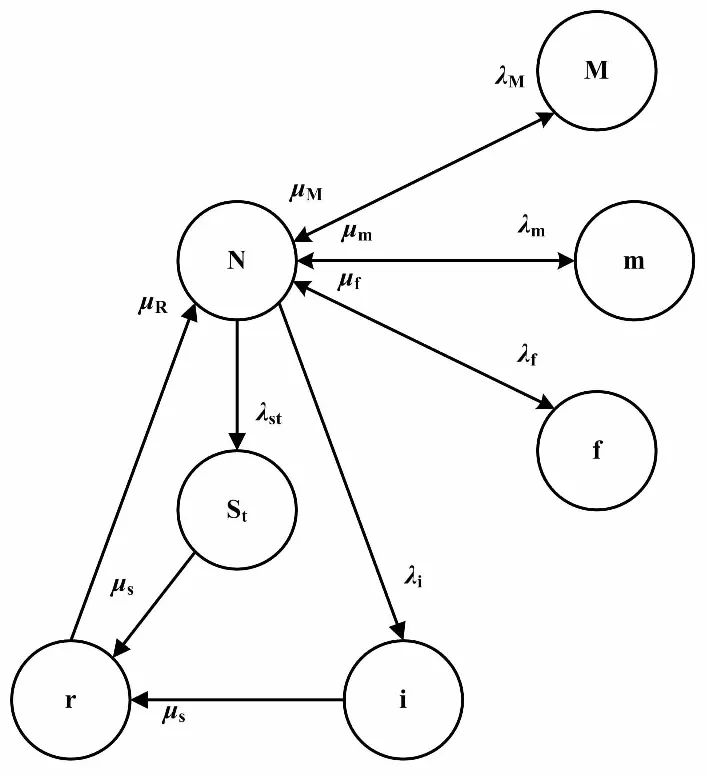
图1 断路器的7状态空间图
由于断路器所具有的故障模式比较多,根据不同位置和运行规则,线路侧断路器的修改计算如式(1)所示[6]。
(1)
式中:λ为线路侧断路器的故障率,次/年;K1为静态系数,取0.3;K2为短路切除系数,取0.4;K3为操作系数,一般取0.3;Li为线路的长度;Lp为平均线路长度;ni为实际运行次数;np为年操作次数的平均值;λp为断路器的故障率。
1.2 发电机、输电线路和变压器模型
发电机、输电线路和变压器模型结构图被定义为3状态图[7]。发电机、输电线路和变压器的转移模型如图2所示。由于故障导致其他元件的状态改变,使邻接断路器无法工作,所以需要相关断路器的动作,才能将故障切除。图2中:λR为故障的出现概率;λM为计划的检修速度;μR为修复的概率;μM为计划修复的概率。

图2 发电机、输电线路和变压器的转移模型图
1.3 母线模型
对于常见的电力连接,母线分为倒闸母线、无倒闸母线等[8]。有倒闸操作的母线可靠度模型如图3所示。参数N为正常操作状态;R为修复故障状态;M是计划的修复状态;S是开关的切换状态;λR为故障发生的概率;λM为计划检修的速度;λS为切换速度;μR为修复的概率;μM为计划修复的概率。

图3 有倒闸操作的母线可靠度模型图
2 电气设备主接线故障
2.1 变电站电气主接线的网络结构特征矩阵
网络结构特征矩阵是评估主接线设备的基本矩阵[9],对主接线之间的关系进行分析。主接线网络结构的变化以及设备中元件的变化都需要由这些特征矩阵进行辅助分析,以便对主接线网络进行整体研究。故障变化的情况主要可分为元件邻接矩阵A、受累停运矩阵D。变电站中的邻近元件的相互关系需要用相对应的矩阵进行描述,主要用于描述相互的影响。对此,可采用元件邻接矩阵满足上述需求。其功能用于对元件组合情况和网络结构状态进行描述,实现主接线系统状态的定量化[10]。
元件邻接矩阵元素用代码(0、1)表示,通过元件间的关联关系来表征元件的运行或停运状况,从而表征变电所电气主接线的系统状态和网络结构。其矩阵表达式如式(2)所示。
A=
x1
x2
⋮

(2)
式中:xi为元件编号,i=1、2、…、n;i、j为元件在矩阵中的排列序号;aij为元件i与元件j的连接关系代码。
(3)
为保证在电力网络结构中不发生故障,需要界定一个影响范围。通过界定范围,可以确定受累停运矩阵表示的被破坏电力元件的故障描述[11]。元件故障的影响范围可用该元件故障所造成的其他元件受累停运状况来表示。因此,受累停运矩阵是以故障元件i为行、受累停运元件j为列得出的,如式(4)所示。
D=
x1
x2
⋮

(4)
式中:dij为停运因子。
受累停运矩阵的停运因子用对元件扩大型故障引起的受累停运元件代码(0、1)来表示。
(5)
受累停运矩阵建立方法流程如图4所示。

图4 受累停运矩阵建立方法流程图
xi、xj是一个元件号码,i,j=1,2,…,n。i、j是矩阵中元件的排序。
①邻接矩阵中调出xi行矩阵,搜索故障影响范围是该步骤的主要目的,进而通过区域的确定进一步诊断故障。搜索的目的是找出代码相对应的元素xj。
②跟踪并调取步骤①搜寻到的各xj行矩阵,继续搜索这些行矩阵中代码1所对应的元件。搜索方式是将代码与元件进行一一对应。
③判断xj中是否存在断路器。若存在,记录该元件编号并停止搜索。若不存在,继续步骤①、步骤②,直到搜索到断路器。此时即完成整个搜索的流程,原则上可以判定为搜索中止,完成该项[12]。
对于搜索所得到的所有记录的行元件,形成一个行矩阵,构建累积停运矩阵,用于表征上述行为。再设计一个xi的行矩阵,以构成累积后的停运矩阵。该矩阵的作用十分重要。
2.2 变电站电气主接线故障应答矩阵
故障类型主要有R型和S型两种。不同故障相对应的后果是不同的。变电站一般都存在R型故障。为了确定R型故障的各类组合对电气主接线的影响,需要合理划分故障类型,对同一类故障采用R型故障进行描述。由于只限于一个元件自身情况,因此,变电站电气主接线的最小路线矩阵在这时是具有相同意义的,也可以用G来表征R型故障矩阵。
而S型矩阵则有所不同。S型故障的结果不仅是故障部件停止运行,而且会使相应断路器分段中的所有非故障部件受到累积停运,从而导致该最小线路断电。
2.3 连续性故障诊断
变电站故障诊断无需通过穷举和筛选就能确定其故障状态,而且往往要根据判断条件进行直接查找。通常以供电中断作为连续性诊断的故障判据。变电站主接线从进线到出线所要经过的元件的集合称为变电站的一条线路。如果在变电站的一条线路中任意除去一个元件就不再是通路,则这条线路称为最小线路。由最小线路构成的集合称为最小线路集。根据最小线路矩阵中元件与最小线路的关联情况,每个元件与最小线路的关联总是非0即1的,所以任意元件都可以将其与最小线路Ln(n为最小线路总数)划分为L(1)和L(0)两部分。假设代码为1的关联通路为x条、代码为0的不关联通道为y条,分别记为Lx(1)和Ly(0),则任意元件的最小线路关联式如式(6)所示。
Ln=Lx(1)∪Ly(0)
(6)
式中:x+y=0,Lx(1)∈Ln,Ly(0)∈Ln。

(7)
3 算例分析
3.1 电气主接线最小割集
本文以最小割集法为主,对单母线的接线进行了研究。根据电力可靠性趋势评价报告公布的可靠参数,经统计后得到主接线元件原始可靠性参数,如表1所示。

表1 主接线元件原始可靠性参数
如表1所示,本算例选取的是SF6断路器。以典型的变电所电气主接线为例,采用单母线接线方式。单母线接线图如图5所示。

图5 单母线接线图
将故障时间与故障率的关系相互联系起来,分别假设故障切换率为μS,对应故障切换时间。元件故障检修修复的概率为μR、计划修复的概率为μM,分别对应故障检修时间和计划检修时间,可以从可靠性参数表中求得修复率。
(8)
同时,参考其他参数,合理地设定拒动修复率的参数。拒动修复率一般设置为μf=396。主接线元件的故障修复率如表2所示。

表2 主接线元件的故障修复率
接下来,求取主接线的最小割集。假设最小线路矩阵中的元件个数为m,求一阶最小割集流程如图6所示。

图6 求一阶最小割集流程图
由该流程可以获取使得各条出线停运的原因。停运时对应的一阶故障状态如表3所示。

表3 停运时对应的一阶故障状态
3.2 计算结果
由表1的出线停运故障状态参数,采用上述方法可以计算出变电站电气主接线各出线停运的概率和频率,主接线各出线停运的概率和频率如表4所示。

表4 主接线各出线停运的概率和频率
由于单母线连接中各出线之间的连接方式相同,具有对称性,导致各出线在单母线连接中停运频率、概率相同。单母线接线简单,操作便利,但由于运行比较单一,一旦断路器关闭,整个回路都会被切断。而发生母线或隔离开关的故障时,母线的回路也要切断。
4 结论
电力设施对经济发展起着至关重要的作用,因此变电站电力设备的稳定运行十分关键。其中,电力主接线系统的可靠性至关重要。电气主接线模型包含断路器、变压器、母线和隔离开关等部件。本文主要研究了变电站主接线的可靠性,总结分析了变电站电气设备主接线可靠性评估的模型及相应指标。本文采用最小割集法,计算了单母线的主接线一阶的最小割集。故障诊断的主要目标是电气设备的供电连续性,反映其可靠性。下一步研究将在分析主接线故障诊断性能的同时,更加合理地解耦厂站接线与电力系统的联系,利用神经网络对设备故障进行辨识,提升自动化水平。此外,变电站分层拓扑也是重点研究方向之一。
