基于改进核极限学习机的短期负荷预测全网模型设计
2021-10-09宫建锋靳盘龙韩一鸣
张 斌,宫建锋,郭 宁,靳盘龙,韩一鸣
(国网宁夏电力有限公司经济技术研究院,宁夏 银川 750002)
0 引言
在电力负荷调度过程中,关键的影响因素之一是短期负荷预测。短期负荷预测在确保电网安全、可靠运行的同时,也能减少电力浪费,并且为更精确预测后续用电数据提供参考[1-3]。预测结果的误差大小对于调节电网系统发供电规划以及为用户创造稳定、经济的用电条件具有直接影响[4-5]。考虑到电能无法大规模存储的特点,在自由化电力市场交易的过程中,需要发电厂出力尽量适应整个系统的负荷波动,达到相对平衡的状态。因此,可以将负荷预测过程理解为预测用户用电需求量的过程。同时,也有学者采用统计学的方法实现对短期负荷的预测,通常包括回归理论分析、时间序列分析等[6]。其中,学者从不同角度实现负荷序列的重构,使模型预测效果获得了显著改善[7]。文献[8]主要以聚类方法寻找相似日,能够实现对某一类相似日或特定时段进行准确识别,并可根据智能预测方法实现对未来负荷的预测功能。文献[9]创建了一种半参数化加法模型,并利用回归框架实现非线性关系和序列误差之间的融合过程。
根据近些年的研究可知,进行短期负载预测,可高效调度发电量,提前做好燃料采购预测等[10-12]。
本文综合考虑子网负荷运行稳定性以及比例系数来完成对全网负荷的预测,以避免因子网参数过少而无法准确预测全网运行状态的问题;然后,给出了基于Cholesky分解的核极限学习机以及短期负荷预测模型,并展开算例分析。
1 改进的核极限学习机算法
1.1 基于Cholesky分解的核极限学习机
通过Cholesky分解求逆的过程取代传统形式的矩阵求逆方法,结果发现可以采用该方法使运算时间明显缩短。采用Cholesky分解方法求解函数Kernel极限学习机(extreme learning machine with Kernel,KELM)输出权值,具体过程如下所示[13-14]。
(1)
(2)
式中:Z为对称矩阵;I为拉格朗日乘子矩阵;θ为输出权值;T为目标矩阵;H为隐含层输出矩阵;C为惩罚参数。
对Cholesky分解方式进行分析,可以发现,这是一种正定分解矩阵。首先证明Z是属于对称正定矩阵。
(3)
现阶段,KELM算法通常以批量学习的方式进行处理,具体方式是把所有测试样本全部输入到学习算法中,经过一次计算得到隐层输出权值,在之后的处理过程中模型不再更新。在每次训练结束后都重新生成一个隐层输出权值,由此完成网络的高效更新,使处理过程变得更加简化。但采用上述方式进行处理时,每次训练都会新增1个样本,导致学习时间明显延长。本文选择Cholesky分解来完成学习过程,先完成部分样本的批量训练,再以增量学习的方式继续训练样本。具体过程如下所示。
以K表示KELM学习的样本数量,则Cholesky分解ZK满足以下条件:
(4)
式中:K()为核函数。
1.2 算法流程
①网络的初始化。
首先,设置总迭代次数、初始学习率、神经元邻域半径;将初始连接权重wj赋值给g个输入输出层神经元,为学习结束设置判断依据[15]。
②竞争学习。
通过计算得到t时输入与输出节点间的欧式距离。从训练样本集中随机选取样本xi,以相距最近输出节点作为最优节点,采用均方绝对值的方法计算初始权重。进一步计算胜利神经元和最优节点权重,并对权重进行更新。最后,迭代输出计算精度。在结果小于最大训练长度的情况下,应继续通过迭代方式调整邻域半径。当两次学习权重误差小于容许误差时,整个学习过程结束。
在二维输出层拓扑结构中,该层节点与邻域节点呈紧密关联的状态,可实现相互学习的功能。因此,相邻节点达到了相近的权重状态,从而完成相近输入节点的匹配过程。本设计以贝叶斯正则化获得的KELM算法来选择相似日的具体流程。
KELM算法流程如图1所示。
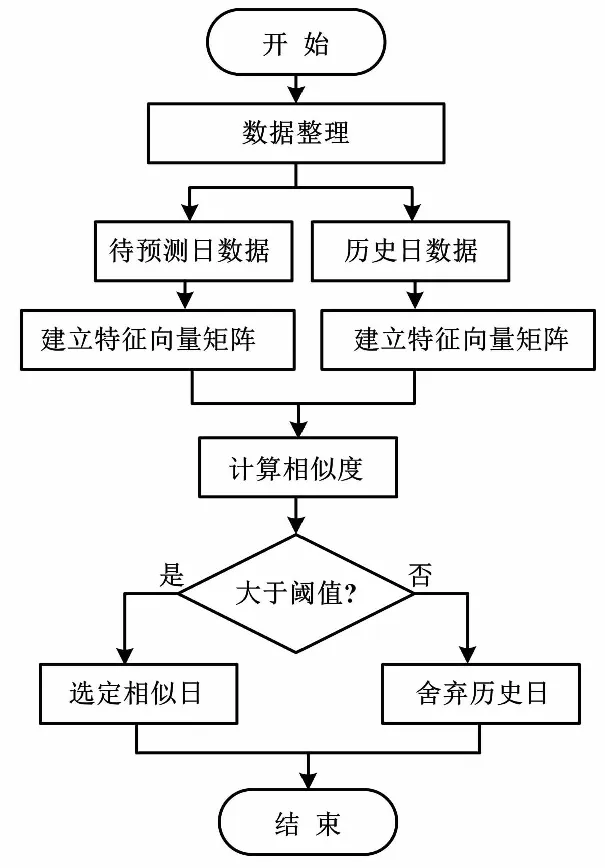
图1 KELM算法流程图
1.3 短期负荷预测模型建立
对短期负荷进行准确、高效预测有助于实现电力系统的长期发展优化,实现精确调度,确保满足各项用电需求,保障电网达到供需动态平衡状态。同时,利用改进后的KELM算法对短期变化趋势进行预测。预测过程如下。
①以宁夏某区域电网作为数据分析对象,采集此电网在2019年11月中的各项用电数据,对其归一化后再提取特征向量参数,并通过聚类方法分成4类样本集。
②把各项数据分为3个部分。
③分别按照改进KELM与聚类改进KELM预测模型,对系统进行计算。
④比较不同条件下获得的预测结果,并根据设定的误差指标完成误差分析。
2 实例分析
2.1 模型建立
本文采用交互验证的方法分析了隐含层中的神经元总数引起的模型泛化性变化,并按照以下步骤进行处理。
①先为隐含层设置初始神经元数量,接着以固定间距逐渐递增。
②对极限学习机模型实施多次预测,再分析交互验证均方根误差(root mean square error of cross validation,RMSECV)。
③按照RMSECV值的最低条件设置隐含层神经元个数。设定初始数量为5,以5个为间隔递增到40个。KELM模型均方根误差曲线如图2所示。根据测试结果可知,误差在神经元数量为25个的情况下达到最低,因此KELM模型采用此参数时最佳。

图2 KELM模型均方根误差曲线
2.2 结果分析
KELM模型的输入变量为待预测日一周之前的t时负荷、两天前t时以及(t-1)时的负荷、一天前t时和(t-1)时对应的负荷,同时还包括温度、湿度参数,以及输出待预测日t时有功功率。分别以(未聚类)改进后KELM方法以及聚类改进KELM方法对4类待预测日欧式距离进行计算,以最小距离条件作为待预测日,同时将其作为极限学习机样本。改进后KELM方法预测曲线如图3所示。
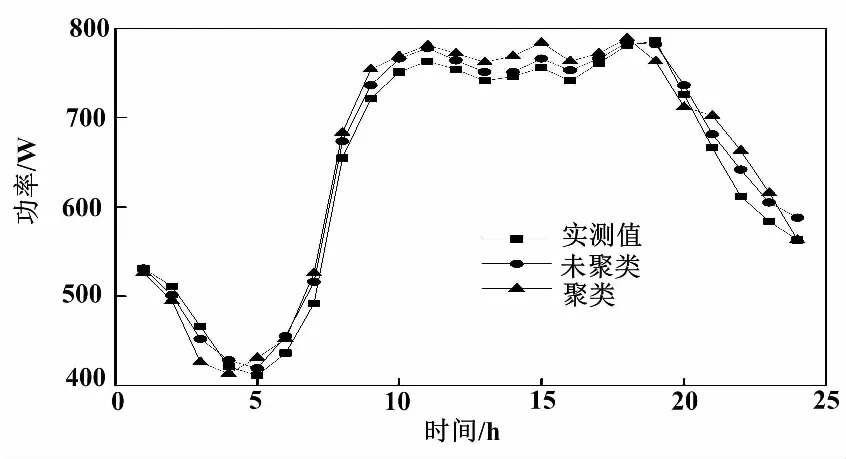
图3 改进后KELM方法预测曲线
改进后KELM方法预测误差对比如表1所示。
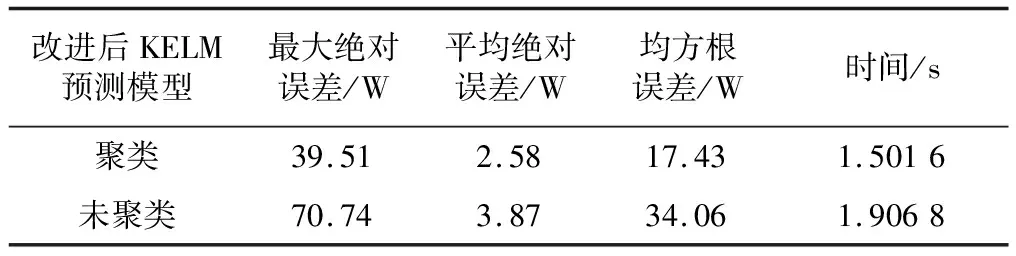
表1 改进后KELM方法预测误差对比
根据图3和表1可知,2种模型依次达到了39.51 W、70.74 W的最大绝对误差,表明采用聚类改进KELM预测模型后系统误差更低,计算精度更高。该结果表明通过聚类方法获得的组合预测模型可靠性更高,能够显著降低模型的预测误差。
2.3 验证准确率
从数据集中选择3个短期负荷作为测试对象,依次为高校用户(A类)、家庭用户(B类)、商业用户(C类)。对各项参数实施初始化赋值。其中,改进KELM方法以同样分类模式共完成5次聚类,得到表2所示的改进KELM方法测试结果。

表2 改进KELM方法测试结果
由表2可知,改进KELM方法计算短期负荷的准确率均在97%以上,满足设计要求。
3 结论
电网公司进行电力调度和配网规划时,需以负荷特征分析结果和日前短期负荷预测作为依据。本文设计了一种经过优化的核极限学习机预测模型,能够实现对子网负荷的快速、准确预测。误差在神经元数量为25个的情况下达到最低,此时KELM模型为最佳模型。按照聚类方式获得的改进KELM模型达到最低值,表现出更强的拟合性能,能够显著降低模型预测误差。使用改进KELM模型总共进行5次聚类,预测到的短期负荷结果准确率均在97%以上,满足设计要求。该设计为改善配网运行经济性提供了参考价值。
