双向水平地震作用效应计算方法对比研究
2021-10-09王亚勇陈才华崔明哲冯旭光陈富盛
王亚勇,陈才华,崔明哲,肖 川,冯旭光,陈富盛
(中国建筑科学研究院有限公司,北京 100013)
0 引言
现行《建筑抗震设计规范》(GB 50010—2010)[1](简称《抗规》)规定,对于质量和刚度分布明显不对称的结构,应计入双向水平地震作用下的扭转影响,采用扭转耦联振型分解法(简称《抗规》方法)计算双向水平地震作用下的扭转耦联地震效应。该方法已在不规则建筑、超限高层建筑结构的抗震分析中广泛应用。
目前国内外设计规范中采用的双向水平地震作用下的效应组合方式主要有两类:一类是先进行两个方向的单向水平地震效应计算,后通过平方和开平方(SRSS)的方式进行方向组合,该方法得到包括我国《抗规》和欧洲规范Eurocode 8[2]在内的多部规范的采用;另一类是将两方向地震作用下的效应以一定比例线性叠加,该方法在欧洲规范Eurocode 8、美国规范ASCE/SEI 7-16[3]、美国加州规范ATC-32[4]等采用。此外,Smeby和Kiureghian[5],Lpez和Torres[6]等提出了一种扩展的完全二次项组合(CQC3)的组合方法,但尚未被广泛采用。对于《抗规》方法的合理性,国内学者和工程界的讨论一直存在,如石诚[7]认为《抗规》方法无法准确计算双向水平地震作用下竖向构件轴力的增大;任胜谦等[8]、白晓红等[9]通过算例的统计分析,对双向水平地震作用下的地震效应组合系数提出了修正建议等。
本文简要介绍了双向水平地震作用效应计算的几种反应谱方法,并提出了一种基于双向地震作用输入的新方法;通过两个算例,对比了各种反应谱方法的计算结果;对各种反应谱方法差异的原因进行了分析,并建议了未来完善双向水平地震作用效应计算方法的研究方向。
1 双向水平地震作用效应SEk的计算方法
1.1 《抗规》SRSS方法
《抗规》第5.2.3条第2款给出了双向水平地震作用下构件效应的计算方法(简称SRSS方法),该方法分为两个步骤。步骤一:采用完全二次项组合(CQC)方法进行振型组合,计算x向、y向单向水平地震作用下的扭转耦联效应分别为Sx和Sy。步骤二:对两个方向单向水平地震作用下的效应按平方和开平方(SRSS)的方式进行方向组合,并取以x向和y向为主向时的效应组合的包络值,即:
(1)
1.2 比例叠加方法
比例叠加方法先计算x向、y向单向水平地震作用下的效应Sx和Sy,再对两单向水平地震作用下的效应按线性叠加的方式进行方向组合,如式(2)所示。线性叠加时,次向水平地震作用下的效应需乘以比例系数α。对于该比例系数α,欧洲规范Eurocode 8和美国规范ASCE/SEI 7-16中规定取为0.3(简称30%方法),美国加州规范ATC-32规定取为0.4(简称40%方法)。
SEk=max(Sx+αSy,Sy+αSx)
(2)
1.3 CQC3方法
Smeby和Kiureghian[5],Lpez和Torres[6]提出的扩展的完全二次项组合(CQC3)的组合方法(简称CQC3方法),计算双向水平地震作用下构件效应的表达式为:
(3)
式中:Sxy为x向和y向地震作用产生的效应之间的耦联项,也采用CQC的方式计算(式(4));γ为次向与主向反应谱值之比;θ为结构主轴方向与地震动主轴方向的夹角。
(4)
式中:ρij为第i振型和第j振型间的耦联系数;Sxi和Syj分别为x向地震作用在第i振型产生的效应和y向地震作用在第j振型产生的效应。
1.4 基于双向地震作用的新方法
从式(1)~(3)可以看出,以上几种计算双向水平地震作用效应的反应谱方法,均是基于“效应组合”,即先输入单向地震作用(单向反应谱)求解效应,然后再对单向地震作用下的效应进行方向组合。本文直接基于“作用组合”提出一种计算双向水平地震作用下构件效应的方法(简称本文方法)。该方法包括四个步骤:
(1)计算单向反应谱输入下各振型的地震作用。按《抗规》第5.2.3条第2款,分别计算x向、y向输入下的第j振型i层质心的水平地震作用标准值向量FXji和FYji。其中,向量FXji和FYji各包含x向、y向和扭转自由度上的三个分量,即向量FXji的分量为FXji,x,FXji,y和FXji,t,向量FYji的分量为FYji,x,FYji,y和FYji,t。
(2)进行双向水平地震作用的组合。分别以x向、y向为地震作用主方向,按主次方向反应谱峰值比值为1∶0.85,对单向反应谱输入下的水平地震作用标准值向量进行线性叠加,并考虑次向地震作用正负号的不同,得到四种作用组合,编号分别为A,B,C,D:
FjiA=FXji+0.85FYji
(5)
FjiB=FXji-0.85FYji
(6)
FjiC=FYji+0.85FXji
(7)
FjiD=FYji-0.85FXji
(8)
注意式(5)~(8)均为向量运算,即向量的每个分量对应地进行加减运算。
(3)按组合后的地震作用求解结构的效应。在结构分析软件中,分别输入式(5)~(8)的四个双向水平地震作用组合,再由结构的刚度矩阵,求解第j振型(j=1,…,m)的效应,对应记为SjA,SjB,SjC和SjD。
(4)进行地震效应的振型组合。分别对四种双向水平地震作用组合下的振型的效应进行CQC组合,得到结构的地震效应SA,SB,SC和SD,以SA为例:
(9)
式中:SjA,SkA分别为地震作用组合A作用下第j振型和第k振型的效应;ρjk为第j振型和第k振型的耦联系数。
取四种地震作用组合下的效应的包络值作为构件设计的依据,即:
SEk=max(SA,SB,SC,SD)
(10)
2 算例对比
本节通过设计规则和不规则的两个框架结构算例,以双向输入弹性时程分析结果为依据,对比第1节所列多种反应谱方法对构件效应计算的准确性。
2.1 算例设计
首先设计了一个简单的双轴对称框架模型,平面布置如图1所示。框架共6层,层高4m;x向5跨、y向3跨,柱距均为9m;柱截面均为800mm×800mm,梁截面均为400mm×800mm。在双轴对称框架模型基础上,保持平面、竖向布置不变,按图1(b)的方式改变外围框架梁和框架柱截面,左、下边榀框架的梁截面减小为300mm×700mm、柱截面减小为600mm×600mm,右、上边榀框架的梁截面增大为400mm×1 000mm、柱截面增大为1 000mm×1 000mm,得到一个双轴不对称模型。
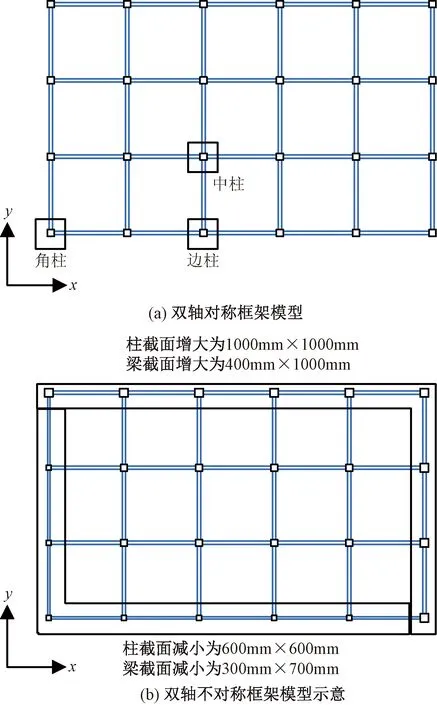
图1 算例平面布置
算例模型的抗震设计参数为:设计地震分组为第一组,抗震设防烈度为7度(0.1g),场地类别为Ⅲ类,特征周期为0.45s,水平地震影响系数最大值为0.08,阻尼比取为5%。
2.2 对比原则
以双向输入弹性时程分析计算得到的构件效应峰值为标定结果,对反应谱方法计算结果的准确性进行评价。为减小地震动时程的离散性对分析结果的影响,按《抗规》小震反应谱生成了7组共14条人工波,两两一组,作为弹性时程分析的地震动输入。所生成的人工波的反应谱与规范谱的对比如图2所示,可见二者吻合较好。
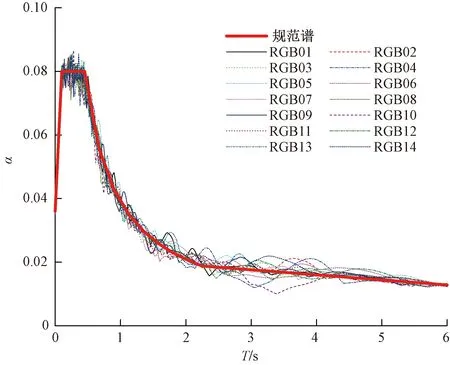
图2 人工波反应谱与规范谱对比
对每组人工波,分别进行4个工况的双向输入弹性时程分析,即xy+(第一个字母表示主波输入轴,第二个字母表示次波输入轴,正负号表示次波沿坐标轴输入的方向,余同),xy-,yx+,yx-,双向地震动时程的峰值加速度比为1∶0.85。双向输入时程分析下构件效应标定值的计算方法为:首先提取上述四个工况的效应包络值作为该组地震波作用下的效应,然后对7组地震波作用下的效应取平均值。
弹性时程分析以及反应谱分析中,30%方法、40%方法和CQC3方法均采用SAP2000计算,对于本文方法则采用PKPM-SATWE计算,由某公司开发了相关的计算补丁程序实现。两个软件的计算参数设置完全相同,并且单向反应谱输入时构件效应计算结果非常接近,可排除不同软件的模型设置、计算假定等对计算结果的影响。
2.3 对比结果
以图1(a)中所示的角柱、边柱和中柱为例,提取各楼层柱在弹性时程分析和反应谱分析中的效应计算结果进行对比。限于篇幅,本节所对比的构件效应为轴力、x向剪力和y向剪力。
双轴对称框架和双轴不对称框架反应谱计算的效应结果与构件效应标定结果(7组地震波作用下的效应平均值)的比值如图3和图4所示,图中还给出了7组地震波时程分析计算的各构件效应的变异系数(时程μ+σ、时程μ-σ)以表征结构在地震作用下的响应的不确定性。可见,对于双轴对称框架(图3),SRSS方法、30%方法计算的角柱轴力偏小,而本文方法计算的角柱轴力偏大;各种计算方法算得的x向剪力和y向剪力均较为接近时程分析结果。对于双轴不对称框架(图4),SRSS方法、30%方法和CQC3方法计算的轴力和y向剪力均偏小,本文方法的计算结果更接近时程分析结果,但角柱的轴力和y向剪力仍偏大。
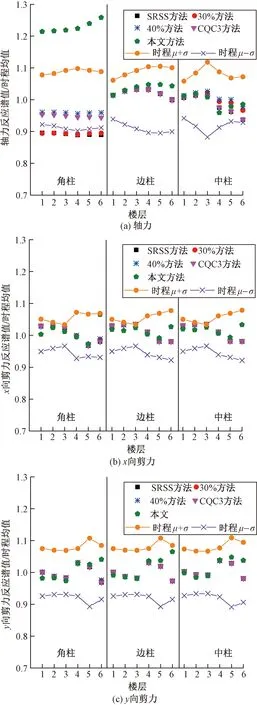
图3 双轴对称框架反应谱方法效应对比
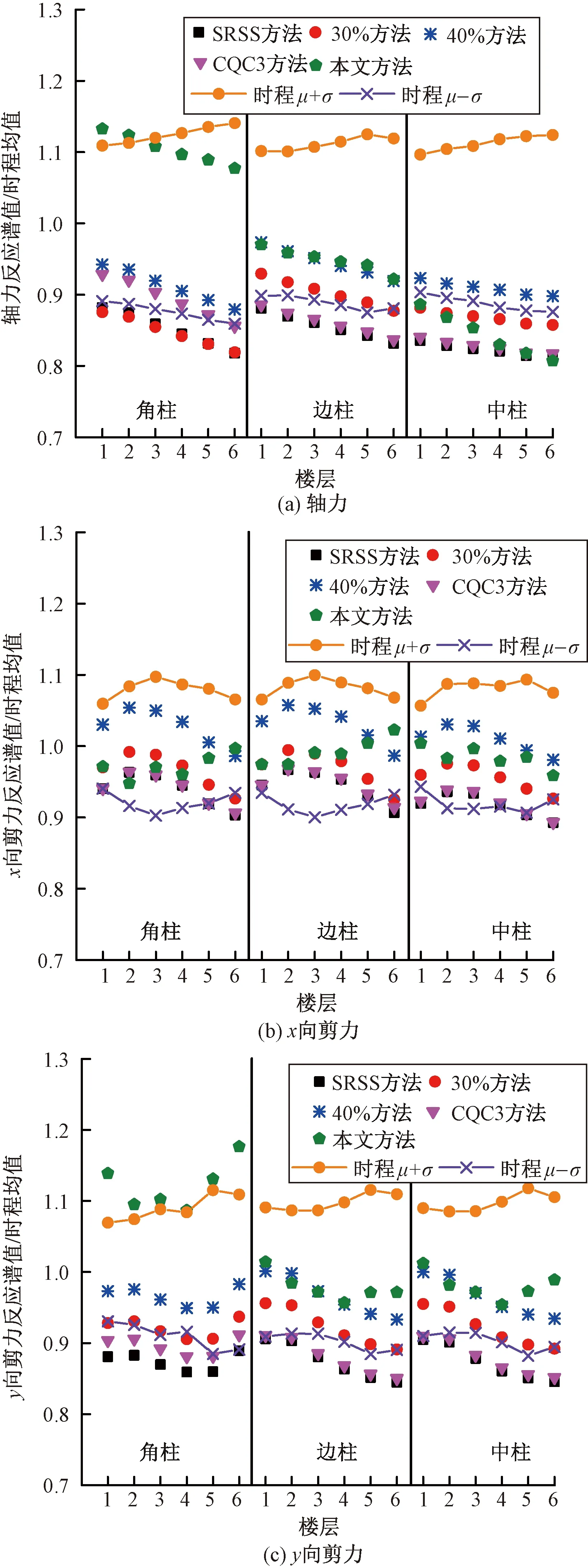
图4 双轴不对称框架反应谱方法效应对比
对两个模型各个构件由反应谱方法计算的效应与时程分析得到的效应之比求平均值和标准差,列于表1和表2,以对比各种方法计算构件效应的整体准确性和离散性。由表1可见,整体而言,对于双轴对称框架,SRSS方法、30%方法、40%方法和CQC3方法计算的轴力和两方向剪力均较为准确,本文方法计算的构件轴力偏大,剪力计算准确性与其他各方法接近。由表2可见,整体而言,对于双轴不对称框架,SRSS方法计算结果明显偏低,即低估了构件在双向水平地震作用下的效应;30%方法、40%方法和CQC3方法计算结果相比SRSS方法有所提高,但仍有一定程度低估;本文方法的计算结果与时程分析结果最为接近。
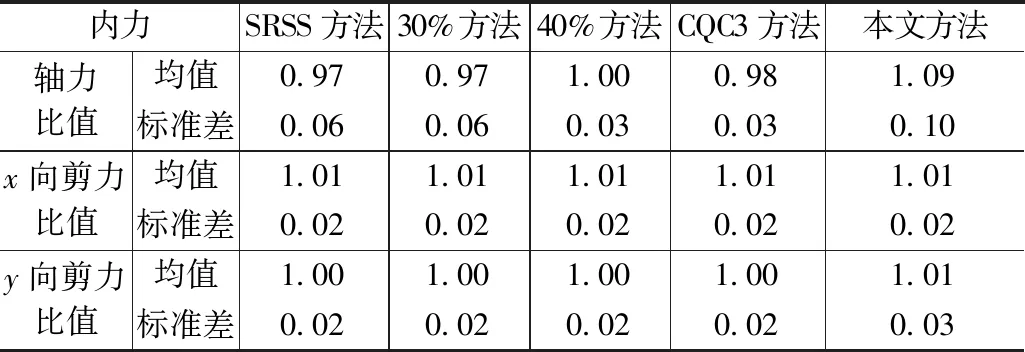
双轴对称框架内力反应谱值与时程均值比值 表1
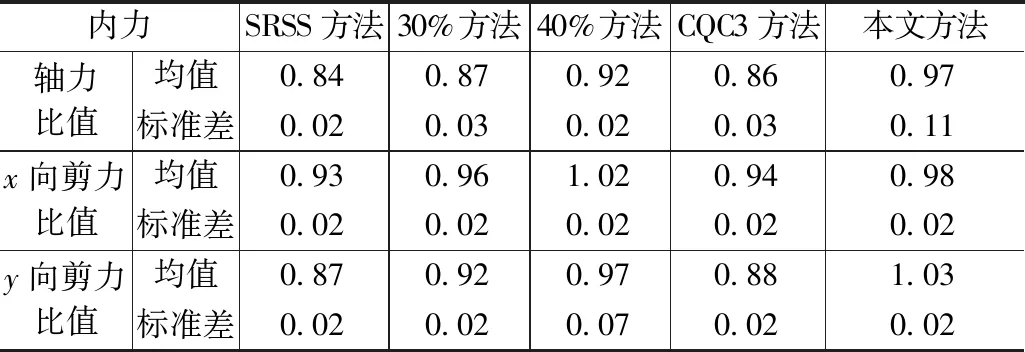
双轴不对称框架内力反应谱值与时程均值比值 表2
3 分析与讨论
3.1 不同方法差异分析
3.1.1 SRSS方法与比例叠加方法
不失一般性,假定x向地震作用效应较大,则SRSS方法计算的效应为:
(11)
比例叠加方法计算的地震效应为:
(12)
图5给出了根据SRSS方法、30%方法和40%方法计算的SEk与Sx的比值随两个方向的地震作用效应的比值Sy/Sx变化的曲线。可见当Sy/Sx在[0,1]区间内时,30%方法和40%方法计算的双向水平地震作用效应与SRSS方法误差较小,其中:30%方法与SRSS方法的最大误差为6%,且大多数情况下都偏于保守;40%方法与SRSS方法的最大误差为10%且在该区间内均偏保守。
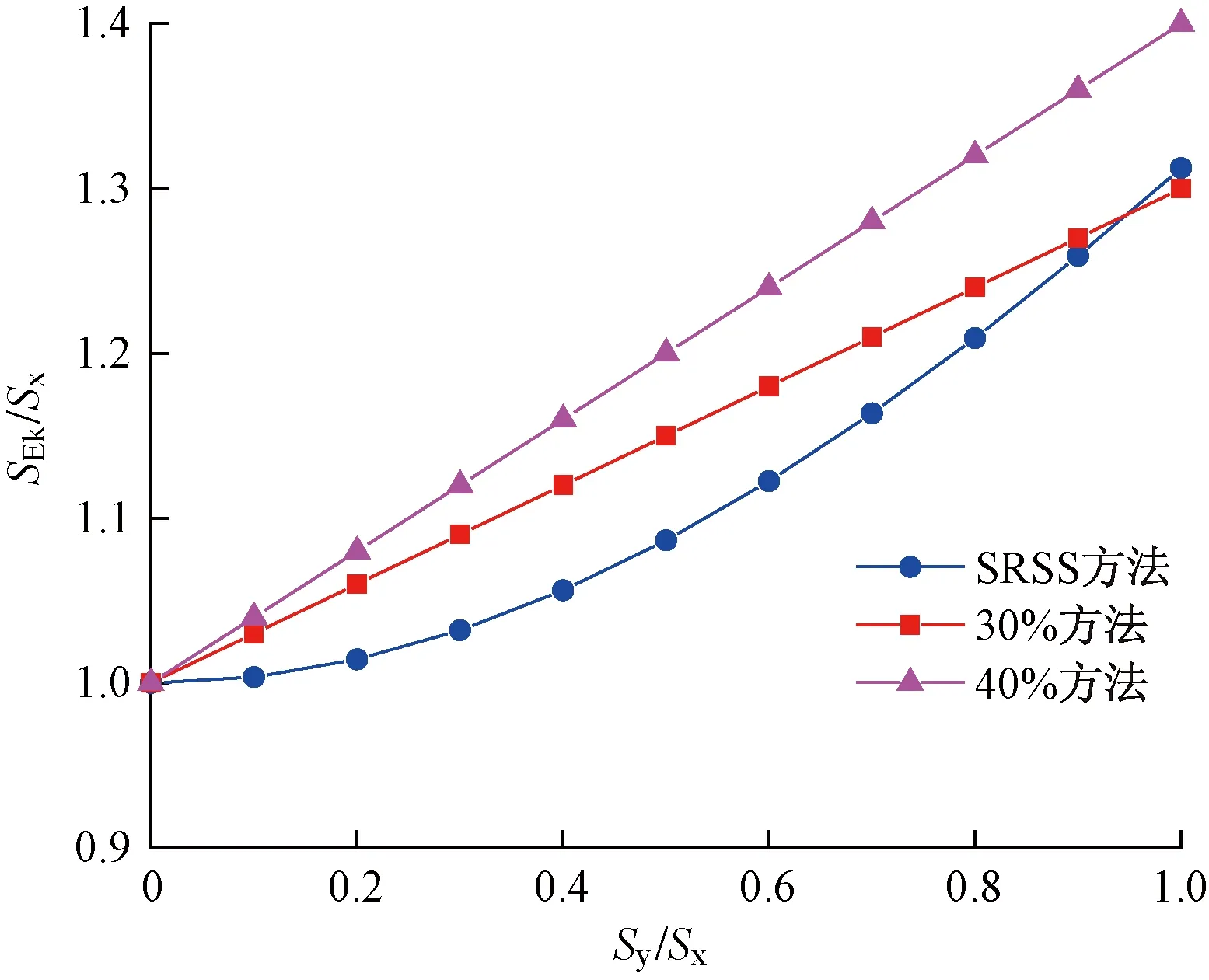
图5 SRSS方法与比例叠加方法对比
可见,比例叠加方法实际上是SRSS方法偏于保守的线性近似,这与算例中结果一致,即30%方法和40%方法的计算结果与SRSS方法较为接近,且比SRSS方法略大。
3.1.2 SRSS方法与CQC3方法
需要指出的是,CQC3方法是在两个地震动主轴方向上的地震作用相互独立的假定下推导的。SRSS方法作为CQC3方法在地震动主轴与结构主轴一致时的特例,同样也忽略了双向水平地震作用之间的相关性,因此可能导致不安全的结果。由本文算例可见,忽略双向水平地震作用间的相关性可能导致角部竖向构件的轴力及不对称结构竖向构件的剪力计算结果明显偏小。
由于CQC3方法不要求地震动主轴与结构主轴重合,而是计算地震动主轴与结构主轴成任意角度时的效应,并取其包络,因此CQC3方法计算的构件效应不小于SRSS方法。但由本文算例可见,CQC3方法也会低估角部竖向构件的轴力及不对称结构竖向构件的剪力。
3.1.3 本文方法
在线弹性假定下,本文方法按式(5)~(8)对各振型下的双向水平地震作用的组合等价于各振型下双向水平地震作用效应的线性叠加,按CQC法振型组合后的构件效应标准值可表示为:
(13)
式(13)与刘季[10]基于双向地震动完全相关的假定推导的效应组合方法基本一致,并增加了考虑地震作用的不同输入方向取效应包络,即对交叉项SxSy取绝对值。时程分析中,双向地震动完全相关意味着两方向的地震动时程符合一定的比例关系,即波形完全一致。
在本文两个算例中,将时程分析所用的地震波主次向均取相同波形输入结构,并按第2节相同的方式对比反应谱方法和弹性时程分析得到的构件效应峰值。将第2节中本文方法误差较大的双轴对称框架的轴力和双轴不对称框架的y向剪力计算结果列于图6。可见,在双向地震动完全相关的情况下,本文方法计算的各构件效应值与时程分析结果接近,而其他几种方法均大幅低估了角柱的轴力和不对称框架模型中框架柱的y向剪力。
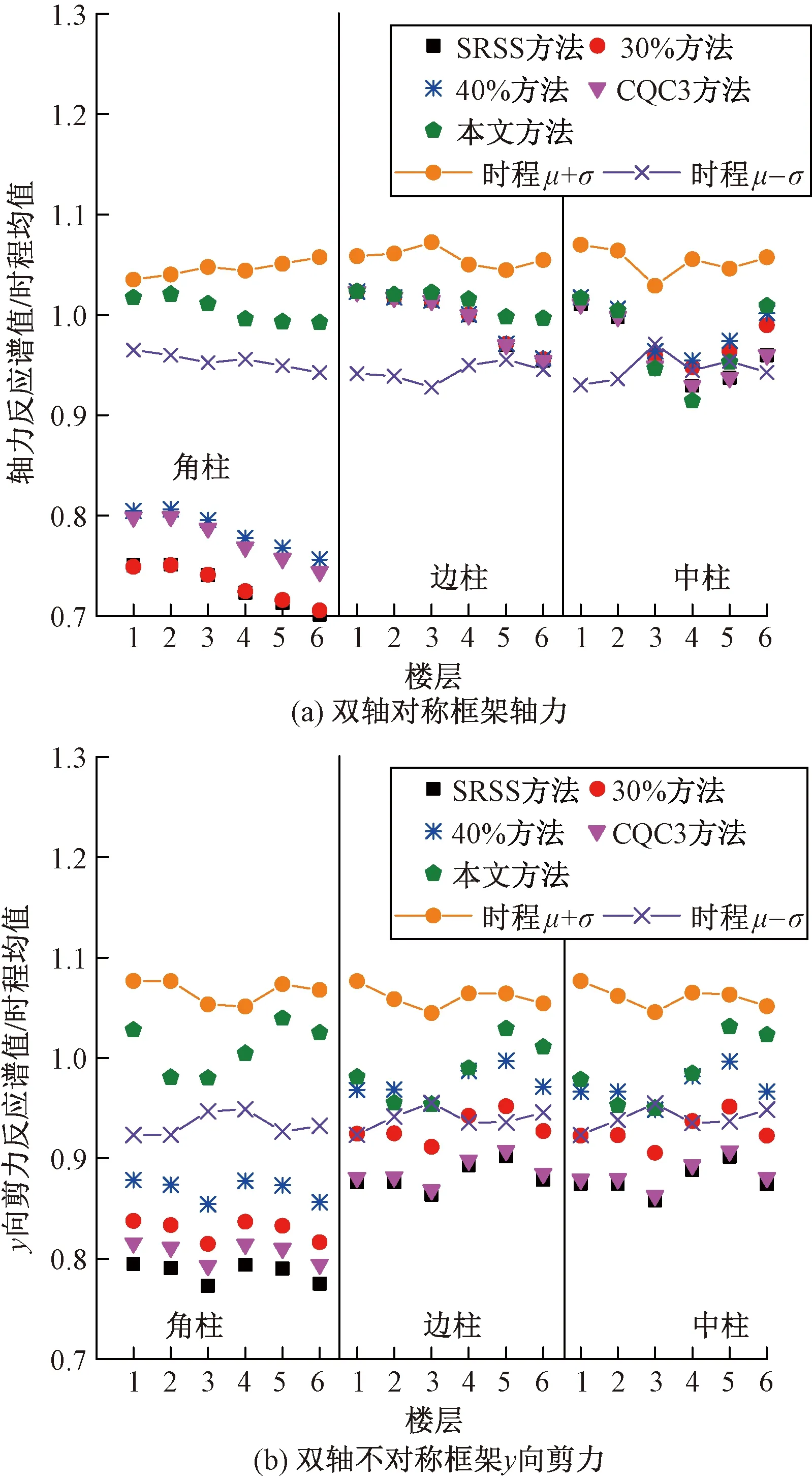
图6 反应谱方法与双向地震动完全相关时程分析效应对比
对于实际的地震作用,两水平分量的地震波波形之间显然存在一定差异,即二者并非完全相关。而本文方法基于两个方向的输入完全相关,因此本文方法计算结果可认为是双向水平地震作用效应的上限值,用于结构设计偏于保守和安全。实际双向水平地震作用输入之间的相关性,仍需进一步深入研究。
3.2 时程分析中地震波双向输入问题
本文进行双向输入弹性时程分析时,除按目前工程实践中的常规做法,将1组地震波交换x,y主向进行输入外,还考虑了次方向地震波沿次轴负向输入的情况,因此对1组地震波共计算了四个工况。表3给出了第2节中算例双轴对称框架1层角柱在7组地震波下的轴力。可见,对于某些地震波(如RGB02,RGB04等),次向地震波沿次轴负向输入时的构件效应大于沿正向输入时的结果;对该算例而言,考虑次向地震波沿次轴正、负向输入计算得到的构件效应包络,比仅考虑次向地震波沿次轴正向输入的结果最大可放大1.52倍(地震波RGB07)。这说明在进行双向输入时程分析时,仅考虑地震波的输入轴而不考虑地震波的输入方向,计算得到的构件效应可能偏不安全。
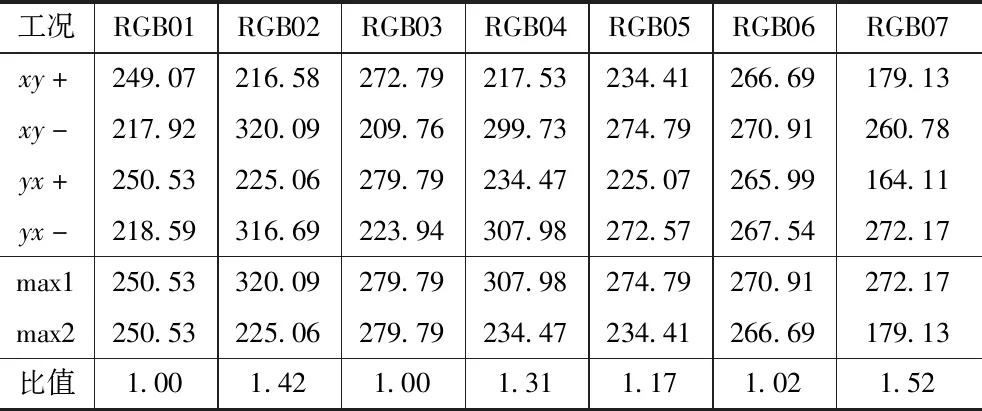
同一构件在不同双向输入工况下的轴力结果 /kN 表3
因此,建议对结构进行双向输入时程分析时,除交换主、次地震波的输入轴外,还应计算次向地震波沿轴负向输入的情况,并对构件效应取包络结果。
4 结论
(1)《抗规》中双向水平地震作用下结构效应计算方法(SRSS方法)由于未考虑双向水平地震作用之间的相关性,效应计算可能偏于不安全,角部竖向构件的轴力和不对称结构竖向构件的剪力计算误差较大,因此结构设计时对于角部竖向构件的轴力、平面不规则结构竖向构件的剪力宜适当放大。
(2)本文提出的双向水平地震作用效应计算新方法基于双向水平地震动完全相关,因此计算结果可认为是双向水平地震作用效应的上限值,用于结构设计偏于保守和安全。
(3)实际的双向水平地震动之间的相关性介于完全不相关和完全相关之间,因此结构在双向水平地震作用下的效应介于《抗规》SRSS方法和本文方法之间。
(4)对结构进行双向输入时程分析时,除交换主、次地震波的输入轴外,还应考虑地震输入的方向,增加次向地震波沿负向输入的情况,并对构件效应取包络结果。
本文方法直接基于双向地震作用,但由于目前缺乏对应于双向输入的双向地震反应谱,因此两个正交方向采用的反应谱完全相同,导致部分构件效应计算结果偏大。未来建议在双向水平地震作用的相关性、双向输入所用反应谱构造等方面开展研究,进一步完善双向水平地震作用效应计算方法。
