k值优化VMD-小波包分析联合降噪方法在隧道爆破信号中的应用❋
2021-10-09王海龙李云赫
王海龙 李云赫 赵 岩
①河北建筑工程学院 土木工程学院(河北张家口,075000)
②河北省土木工程诊断、改造与抗灾重点试验室(河北张家口,075000)
③中国矿业大学(北京)力学与建筑工程学院(北京,100083)
引言
爆破施工是隧道掘进最常用的破岩方式,它所带来的结构振动极有可能对在建隧道及周围建筑物产生损害。爆破实测现场环境复杂,爆破振动信号不可避免地会受到外界环境的影响。因此,对爆破振动实测信号进行降噪处理对后续的信号分析具有重要的实际意义[1]。
传统傅里叶变换用于处理平稳信号具有良好的分析效果,但不适用于非平稳、非线性的爆破振动信号[2];短时傅里叶变换在传统傅里叶变换的理论基础上引入窗函数获取时域信息,但仍无法满足非稳态信号变化的频率需求[3];小波变换方法解决了傅里叶变换窗口大小不能随频率变化的问题,但在去噪过程中要进行阈值和基函数的选择,缺乏自适应性[4];经验模态分解(EMD)与局域均值分解(LMD)克服了用户设置基函数盲目性问题,但无法避免模态混叠等问题[5-6];总体平均经验模态分解(EEMD)在分解初始加入一定量的白噪声,一定程度上减弱了模态混叠现象,但其不稳定性和计算程序复杂的缺点仍未得到解决[7];互补集合经验模态分解(CEEMD)使用正白噪声和负白噪声来增加额外的噪声,但是其在分解时会出现较多的伪分量[8]。
本文中,针对隧道爆破振动信号采集过程中存在的强噪声干扰问题和利用变分模态分解(variational mode decomposition,简称VMD)方法进行信号分析时关键参数非最优问题,提出一种基于优化k值的VMD联合小波包分析的降噪方法[9-10]。该方法兼具VMD和小波包分析的优点。从能量守恒的角度确定最优分解层数,在非递归的理论框架下,通过构造并求解约束变分问题实现信号分解。克服了模态混叠和计算量大等问题,表现出良好的噪声鲁棒性。
1 VMD参数优化原理
1.1 VMD原理
VMD算法一次性将复杂信号分解为k个调幅-调频信号[11],表达式为

式中:Ak(t)为uk(t)的瞬时幅值;φk(t)作为中间参数,对其求导可得各个调幅-调频信号的中心频率ωk(t),即ωk(t)=φk′(t)。
通过控制带宽来避免模态混叠现象,构造约束变分问题,表达式[12]如下:

为实现将约束变分问题转变为非约束变分问题,引入惩罚因子α和Lagrange乘法算子λ(t),构造增广Lagrange表达式:

经过傅里叶等距变换等过程可得到
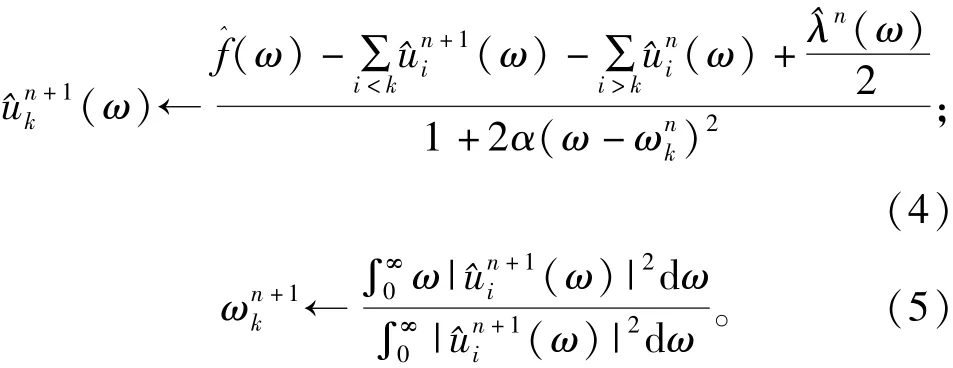
^uk(ω)经过两次傅里叶逆变换,由频域转换到时域,进而求解实部uk(t),实现将信号分解为k个模态分量。
1.2 模态数k优化准则
VMD过程遵循能量守恒原则,故可从各模态分量与原始信号之间的能量关系入手,对VMD算法参数进行优化。当VMD分解程度过大,即k值过大时,由于存在过分解的分量,分量能量线性之和大于原始信号的能量,并不合理。因此,从能量守恒的角度优化VMD模态数k显得尤为重要。
原信号或分量信号的能量计算公式为

式中:E为信号的能量;x(i)为信号序列;n为采样点数。
同一信号在VMD算法中设定不同模态数k分解后,模态分量能量线性总和大小不同,为评价信号在不同模态数k值分解后分解程度水平,引入分解能量差值参数λ,公式为:
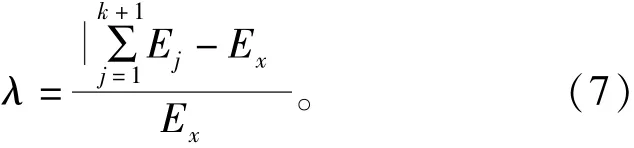
式中:Ex为原信号的总能量;Ej为原信号经VMD处理后对应的第j个模态分量的能量。
由式(7)可知:λ的大小与分解程度呈正相关,λ越大,过分解现象越严重;而λ越接近或等于零,则说明分解程度趋于合适。
绘制k-λ曲线。基于等能量分解原理,VMD模态数k优化步骤如下:在k逐次增加的条件下依次对信号进行VMD预处理,分别计算分解能量差值参数λ;当λ出现明显突变时停止计算,取突变点处对应的k为最优模态数。
2 k值优化VMD-小波包分析联合降噪原理
2.1 小波包降噪原理
实现小波降噪过程时,首先自定义小波基函数对含噪信号进行分解,再对高频分量进行阈值滤波,最后重构信号得到降噪信号[13]。小波包分析以小波变换为基础,对小波变换中未处理的高频分量再次细化分解。相比于小波降噪,小波包分析具有更高的时频分辨率,可以进一步消除高频部分存在的噪声余量,提高去噪精度[14]。
2.2 k值优化VMD-小波包分析联合降噪
图1 为基于k值优化的VMD-小波包分析联合降噪流程图。首先,将原始爆破振动信号利用基于k值优化的VMD法进行分解,得到k个模态分量;通过比较相关系数、方差贡献率两个指标,筛选出包含噪声的模态分量,并对筛选出的含噪分量利用小波包分析做阈值降噪处理;最后,将降噪处理后的含噪分量与优势分量重构,得到纯净信号。
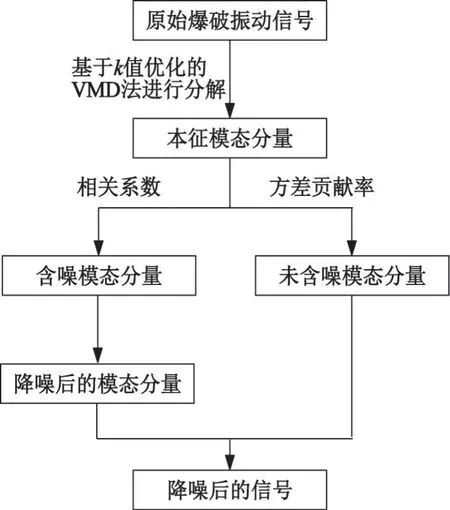
图1 降噪流程图Fig.1 Flow diagram of denoising
3 仿真分析
构造多频信号叠加仿真信号,表达式为
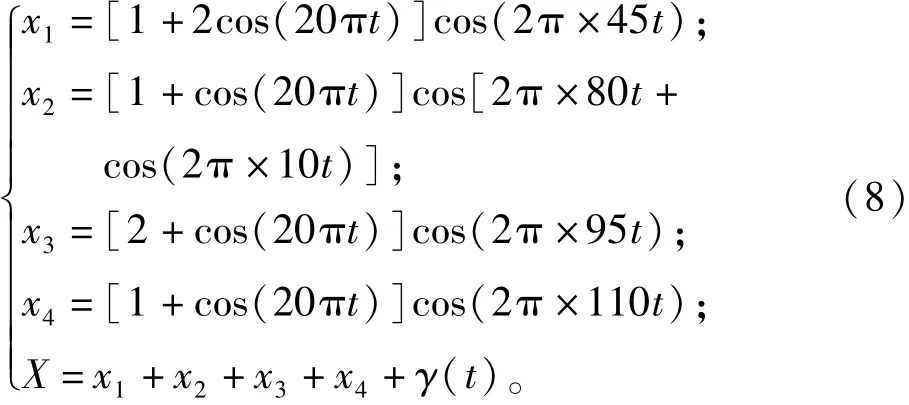
式中:γ(t)为人工噪声。
VMD算法中分解完备性平衡参数α取默认值2000[15],利用Matlab软件做仿真信号分析,信号时域波形如图2所示。在不同k值条件下,依次对仿真信号进行VMD预处理,并分别计算原信号能量和各模态分量能量之和,结果如表1所示。
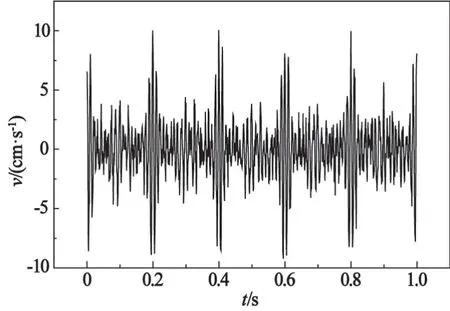
图2 多频叠加信号时域图Fig.2 Time-domain diagram of multi-frequency superposition signals
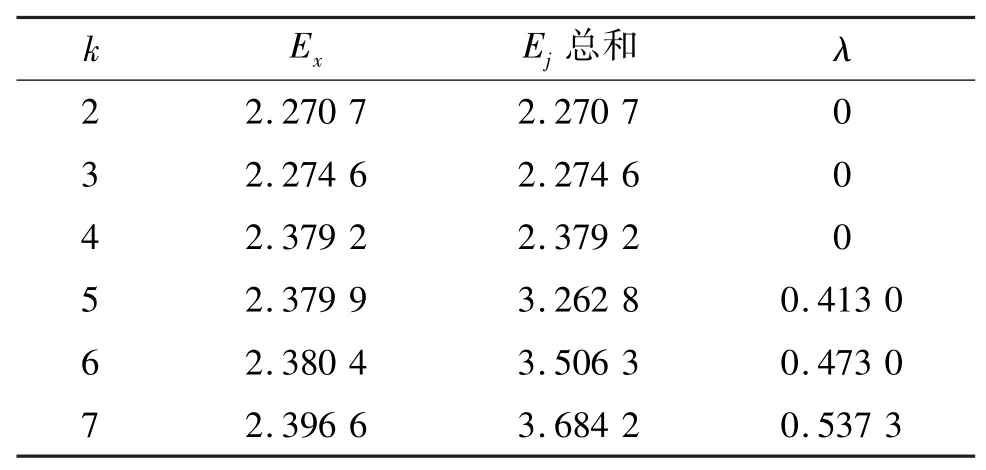
表1 仿真信号VMD各能量参数Tab.1 Energy parameters of VMD of simulation signals
原信号中由于存在人工噪声的干扰,所以在不同的k值条件下总能量Ex不严格相等,存在波动现象。直观分析表1可得:当k≤4时,λ恒等于0,即信号经VMD处理后各模态分量能量之和严格等于原信号能量;从k=5开始,由于存在虚构的分量,λ逐渐增大。
根据上述模态数和选择准则,将突变点k=4取为最佳分解层数。探讨信号在此参数下的分解水平,进一步分析VMD信号的频谱特征,如图3、图4所示。结合图4中的频谱图,仿真信号由4组多频信号和人工噪声组成,在k=4的条件下,经过VMD处理的信号u1、u2、u3、u4分别为主频为45、81、95、110 Hz的单信号,各分量信号的特征频率与原始仿真信号有1 Hz的差别,均在允许误差范围内。由此可以验证,基于k值优化的VMD法分解效果较好。
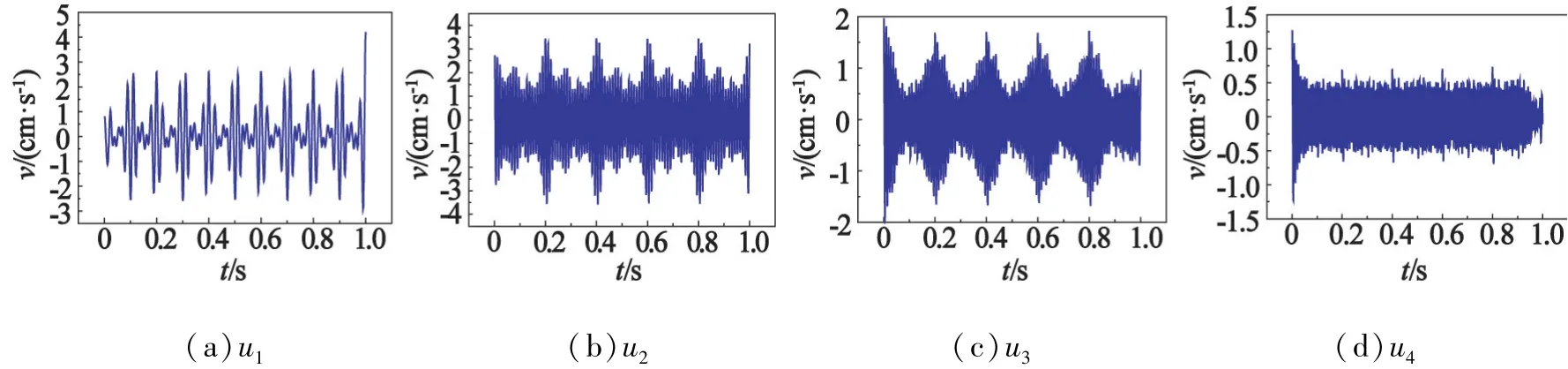
图3 仿真信号VMD各分量的时域Fig.3 Time-domain of VMD of simulation signals
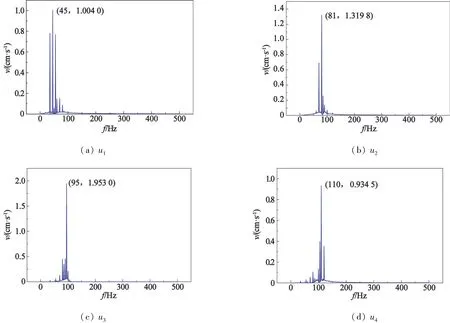
图4 仿真信号VMD各分量的频域Fig.4 Frequency-domain of VMD of simulation signals
针对于上述模拟信号,利用基于k值优化的VMD将其分解为一系列本征模态分量,利用Matlab中互相关函数的概念计算各个模态分量与原始信号的相关性,并依据相关性绝对值的大小对筛选出需要进行处理的含噪分量进行降噪处理,将处理后的结果与未经处理的模态分量重构得到最终的纯净信号[16]。降噪处理后的纯净信号与原始仿真信号及初始信号的对比关系如图5所示。
由图5(a)和图5(c)可看出,处理后的纯净信号在保留仿真信号特征信息的同时,基本剔除了隐藏于其中的噪声信息,且降噪后的信号较原始波形曲线更为光滑,降噪效果良好。从图5(b)和图5(c)可以看出,去噪后的纯净信号与初始信号在信号峰值及局部波形特征上的相似吻合度较好。
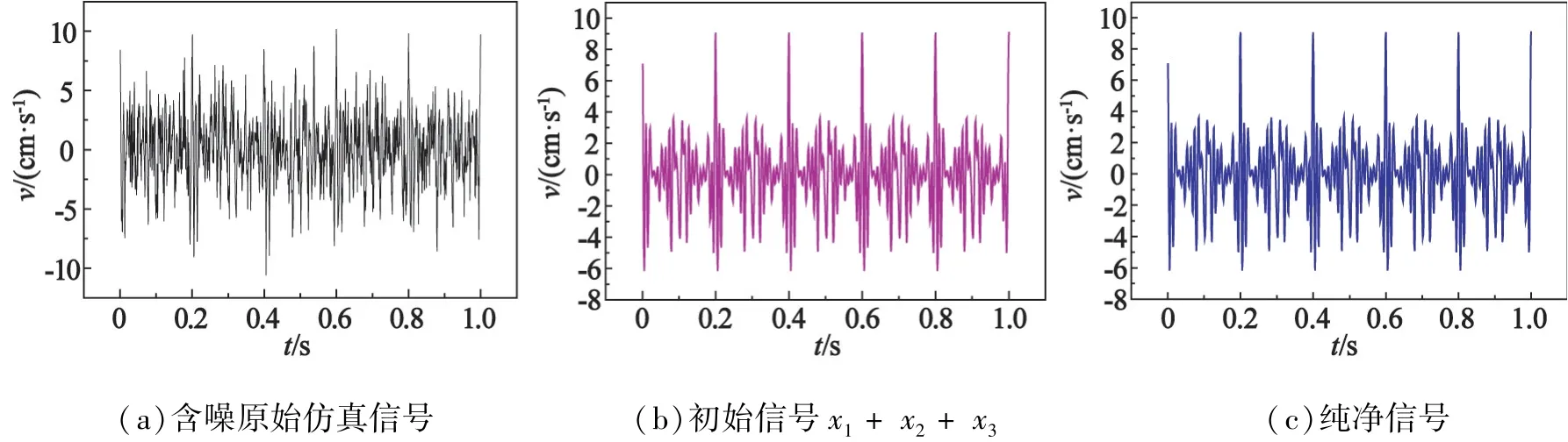
图5 经降噪处理后的纯净信号与原始仿真信号及初始信号的对比Fig.5 Comparison of the pure signal after denoising with the original simulation signal and the initial signal
为了进一步研究两种信号的相似程度,利用Matlab中互相关函数corrcoef进行计算,得到纯净信号与仿真信号的相关系数为0.962 3,去噪后的信号与初始信号表现出较好的相关性。综上所述,基于k值优化的VMD联合小波包阈值去噪方法在仿真信号领域应用效果良好,为后续对实测爆破振动信号的降噪处理提供了一定的理论基础。
4工程实例分析
4.1 工程背景
试验以新建河北省张家口市太子城至内蒙古自治区锡林浩特段崇礼隧道爆破施工工程为背景。全断面爆破施工,使用1~13段非电毫秒雷管和2#岩石乳化炸药,最大单段药量43.2 kg,循环爆破总药量204 kg。采用TC-4850N爆破振动监测仪采集到的某次爆破施工中爆破振速原始信号,如图6所示。从图6可知,受爆破施工现场复杂环境的影响,爆破振速时程曲线中夹杂着各种毛刺噪声信号。
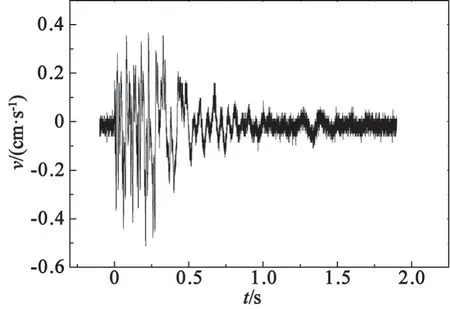
图6 原始爆破振动信号时域波形图Fig.6 Time-domain waveform of original blasting vibration signals
4.2 基于k值优化VMD-小波包阈值联合降噪实现
采用上述分析理论,对采集到的隧道爆破振动信号在不同的k值条件下进行VMD预处理,并分别计算原信号能量Ex、各分量的能量Ej总和∑Ej、分解能量差值参数λ,直到λ出现较明显的变化,停止计算。
计算结果如表2所示。
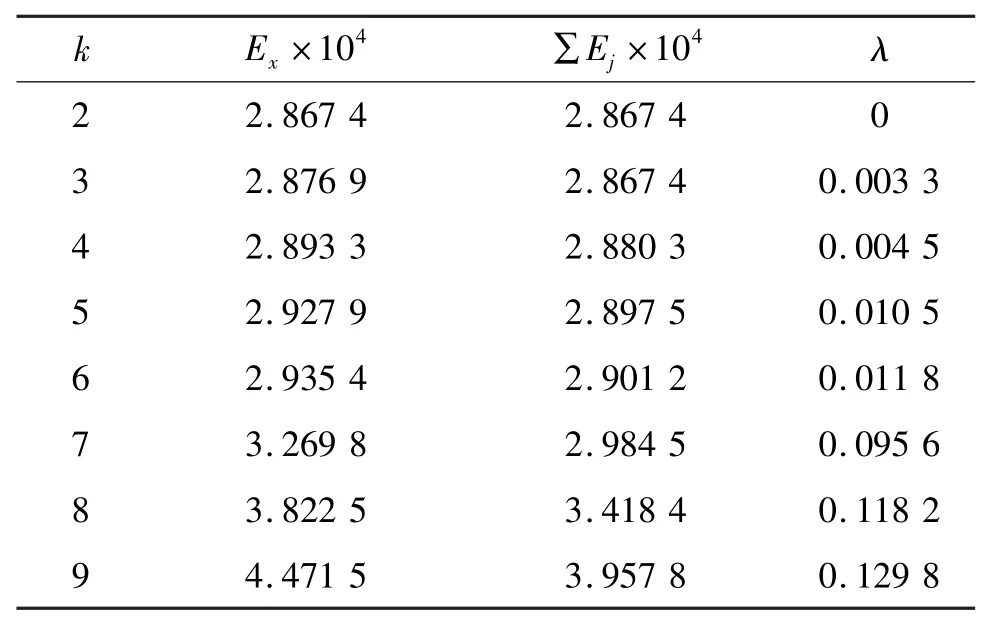
表2 爆破振动信号VMD处理后的各能量参数Tab.2 Energy parameters of blasting vibration signals after VMD
由表2可看出:当k=2时,λ严格等于0;k=3~6时,λ出现0.003 3~0.011 8之间的微小波动,但波动范围较小,可认为仍处于平稳无突变状态;而在k=7时,λ陡增至0.095 6,随后不断地增加。故判定k=6是λ的变化转折点。按照模态数k选取准则,将k=6取为VMD最优分解层数,并由此对爆破振动信号进行VMD处理。各个模态分量的时程曲线见图7。
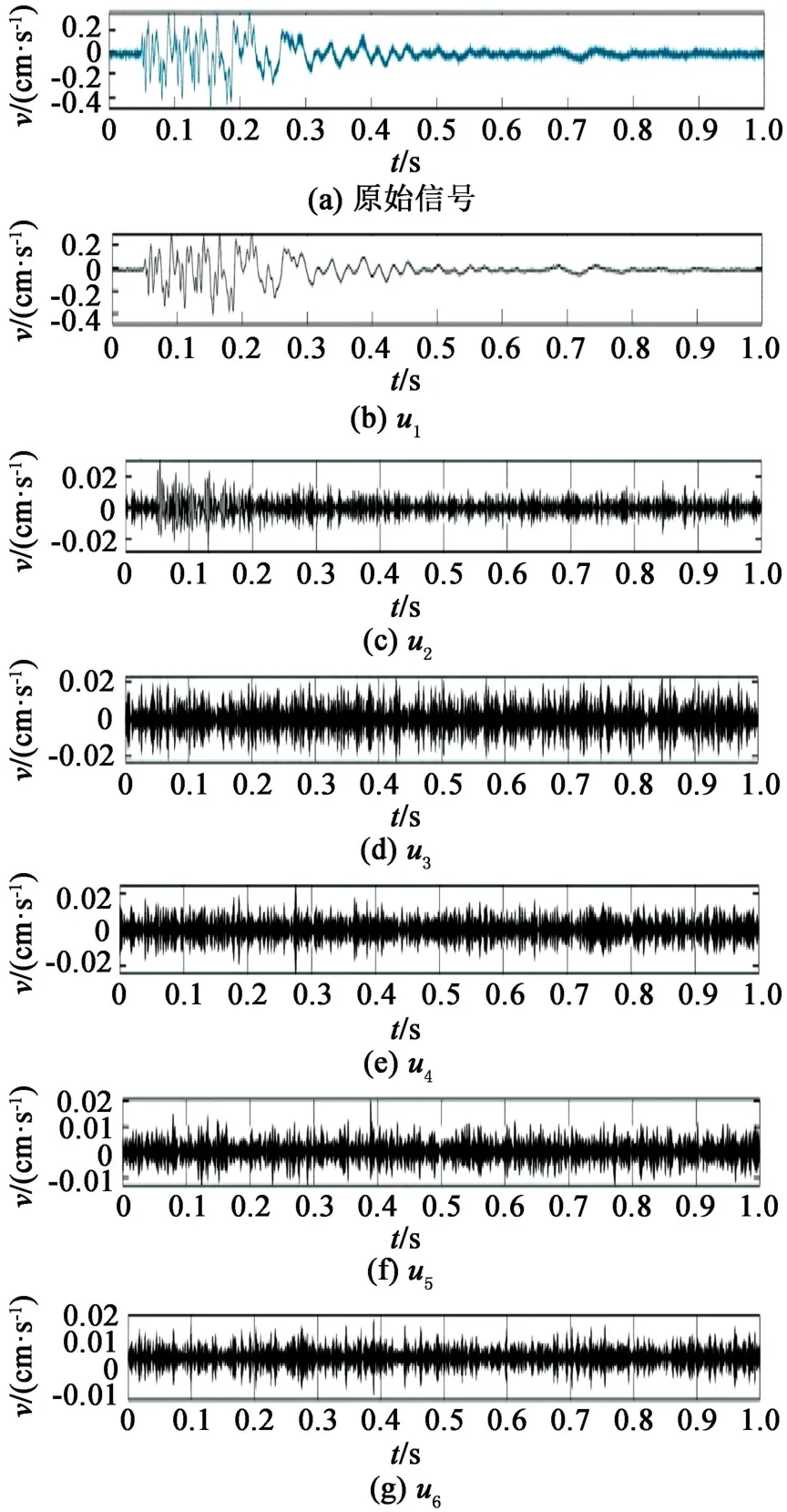
图7 爆破振动信号各模态分量时程曲线Fig.7 Time history curve of each modal component of blasting vibration signals
根据式(9)计算每一个模态分量与原始爆破信号的相关系数ri,计算结果见表3。
3.2.1 基本信息管理模块。完成校企双方指导老师、顶岗实习学生个人基本信息的维护和查询功能。校内指导老师的基本信息应包括:系部、姓名、邮箱、QQ、联系电话等。企业指导老师的基本信息应包括:姓名、联系电话、邮箱、QQ、企业名称、企业地址、工作岗位等。学生的基本信息应包括:学号、姓名、系别、班级、联系电话、邮箱、QQ、实习单位名称、实习单位地址及实习岗位等。

表3 模态分量的相关系数Tab.3 Correlation coefficient of intrinsic mode function
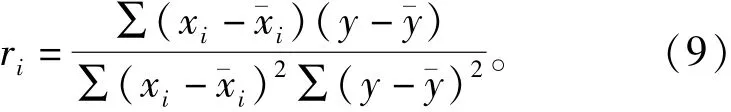
式中:xi表示各模态分量;y表示原始爆破信号;ˉxi、ˉy分别为xi、y的平均值。
分析表3可得,经VMD处理后的各模态分量与原始信号的相关系数差异较大。其中,u4、u5、u6相关系数均小于0.15,初步判定为含有较多噪声的含噪分量;其余分量可以看作是优势模态分量。
定义模态分量平方的算术平均值与其均值的平方之差为模态分量的方差s,通过各个模态分量的方差贡献率ε校核上述选择的可行性[12,17]。模态分量的方差及方差贡献率计算如下:
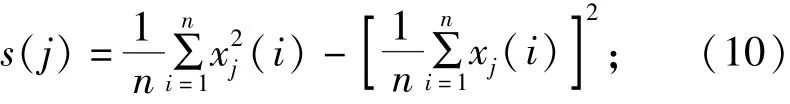
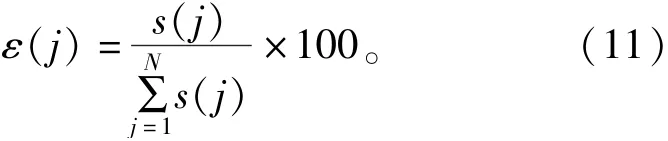
计算得到各模态分量的方差贡献率,见表4。

表4 模态分量的方差贡献率Tab.4 Variance contribution rate of intrinsic mode function
由表4可知,u1、u2、u3模态分量的方差贡献率较大。将相关性较差、方差贡献率较小的u4、u5、u6重构得到新的分量u′,以u′作为新信号进行小波包分析。工程爆破中的振动频率一般在100 Hz左右,既要保证采集到的信号完整,又要避免引入高频信号,故需要将采样频率设为信号频率的10~100倍。结合前期爆破振动监测试验,本次监测将爆破振动监测仪TC-4850N的信号采样频率设置为5 000 Hz。
综合考虑支撑长度、消失矩、对称性、正则性以及相似性等因素,结合采样定理[16],选择具有良好紧支撑系性、光滑性及近似对称性的db8小波基函数。选取分解层数为3、5、7和9进行仿真计算。结果显示,在分解层数为7时,去噪效果最佳,然后利用默认的软阈值函数进行降噪处理[14]。
最后,将降噪处理过的含噪分量u′与优势分量u1、u2、u3重构,得到最终的纯净信号,如图8所示。由图8可知,与原始信号相比,经VMD-小波包阈值联合降噪后的纯净信号在保证局部波形特征及峰值不变的基础上,基本消除了原始信号中存在的噪声分量。

图8 基于k值优化VMD联合小波包阈值降噪前、后信号的对比Fig.8 Comparison of signals before and after threshold denoising by k-value optimization VMD combined with wavelet packet
4.3 降噪效果评价
通常利用信噪比η和均方根差μ两种指标衡量爆破振动信号降噪效果。信噪比越大,均方根差越小,则降噪效果越好[18]。信噪比、均方根差的计算公式为
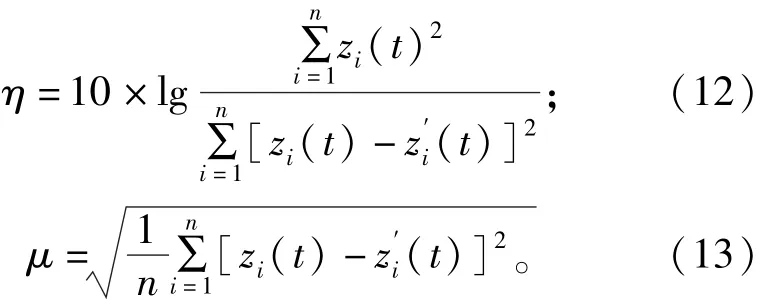
式中:zi(t)为原始信号为经降噪处理后的信号;n为信号长度。
评价VMD联合小波包降噪效果的同时,再次验证VMD法中模态数选择是否为最佳。分别选取不同k值的VMD联合小波包对信号进行上述降噪操作,并计算信噪比、均方根误差,计算结果见表5。从表5中可知,k=6时,降噪效果最好。
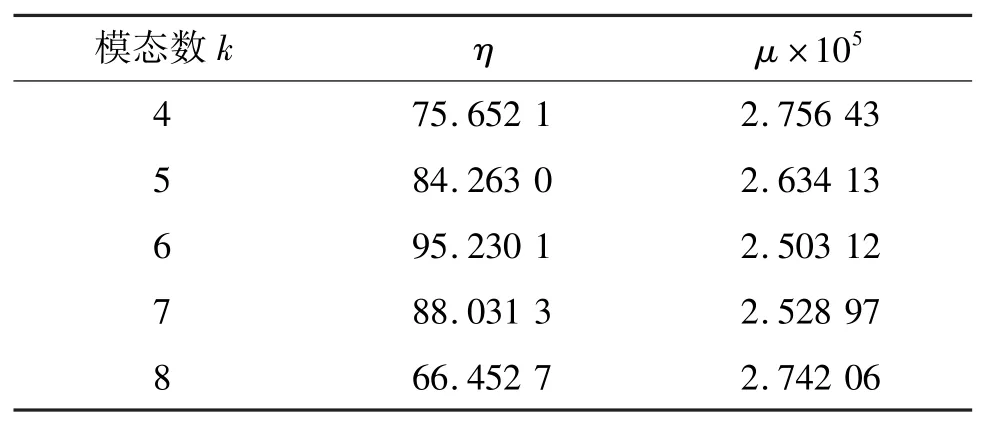
表5 不同k值的VMD联合小波包阈值降噪效果对比Tab.5 Comparison of threshold denoising effects of VMD with different k-values combined with wavelet packet
为进一步验证此方法的降噪效果,对实测爆破振动信号分别采用小波包阈值降噪法、EMD-小波包联合降噪法、CEEMD-小波包联合降噪法进行分析,与VMD-小波包联合降噪法的对比结果见表6。

表6 降噪效果对比Tab.6 Denoising effect comparison
对比分析可得,经k值优化的VMD-小波包联合降噪法的信噪比(95.230 1)最大,均方根差最小(2.503 12×10-5),降噪效果较好。
5 结论
1)VMD方法基于等能量理论模态数选取准则确定参数k,能有效避免信号分解不足或过分解。
2)实际工程中采集到的原始含噪信号经过k值优化VMD-小波包阈值法联合降噪后,可以在消除噪声的同时,有效地保留原始信号中的细节特征,为后续准确分析爆破信号奠定了基础。
3)与小波包阈值降噪法、EMD-小波包联合降噪法、CEEMD-小波包联合降噪法相比,k值优化的VMD-小波包联合降噪方法信噪比大,均方根差小,降噪效果较好。
