DNAN基熔铸装药榴弹跌落冲击特性与安全性分析❋
2021-10-09沙洪博袁俊明黄求安邢曦伟
沙洪博 袁俊明 黄求安 夏 韬 邢曦伟 温 旭
①中北大学环境与安全工程学院(山西太原,030051)
②中国兵器装备集团自动化研究所有限公司智能制造事业部(四川绵阳,621000)
引言
在运输过程中,由于各种意外原因,弹药会发生跌落或撞击,可能会造成弹体变形、弹药损伤加深及炸药稳定性降低。弹药损伤加重会导致弹药性能劣化,影响爆轰波的传递,减弱弹药毁伤效果;炸药的稳定性降低会导致炸药在受到外界刺激时,易发生点火和爆炸等意外事件,引起人员伤亡。
跌落试验是评价弹体安全性的重要试验之一,众多学者对此系统地进行了研究。南宇翔等[1]采用ANSYS/LS-DYNA软件模拟了子弹在不同工况下的冲击特性及子弹降落的角度和速度对子弹过载峰值的影响。代晓淦等[2]以PBX-2炸药为例,设计了炸药加速模拟跌落试验装置,分析了在壳体约束条件下的PBX-2跌落响应过程,并与Spigot试验做对比,验证了约束条件对弹药跌落反应的影响。王晨等[3]应用点火增长反应速率方程、炸药热力耦合和自热反应模型描述了在跌落过程中炸药的起爆和破碎过程,并实现了对炸药跌落响应的分析。高大元等[4]设计了炸药撞击试验,分析了跌落高度和弹药老化对炸药安全性的影响。Dienes等[5]针对热点引起炸药爆炸的可能性,比较了几种机理,认为闭合裂纹的界面摩擦引起爆炸的可能性较高。Bennett等[6]开发并演示了PBX(高聚物黏结炸药)的数值本构模型;该模型可用于预测高能材料的非冲击点火和机械响应,并用于预测弹药跌落对炸药的损伤。Yang等[7]采用二维力学化学模拟,通过流体力学代码DREXH-2D,有效地描述了PBX受到中低水平撞击时的力学和点火爆燃响应,并应用计算模型准确预测了炸药意外起爆时的动态响应。
综上所述,国内外专家针对跌落对PBX损伤的影响进行了全面的研究,主要进行了宏观跌落试验以及细观模拟点火分析,而针对DNAN(2,4-二硝基苯甲醚)基熔铸炸药在跌落过程中受到应力载荷以及冲击加速度的变化规律缺乏系统性研究。
DNAN基熔铸炸药塑性变形能力低,在跌落过程中易发生断裂。同时,DNAN基熔铸炸药在装药过程中易出现缩孔、缩松、裂纹及孔洞等缺陷;在跌落撞击过程中,装药缺陷易引发热点,造成爆炸,引起人员伤亡。所以,开展DNAN基熔铸装药弹体在意外刺激作用下的力学响应特性及安全性分析具有重要的工程应用价值和现实意义。
在跌落过程中,含DNAN基熔铸装药榴弹的主装药受低幅值、长脉冲的低速冲击力作用而易产生损伤,形成热点,诱发成燃烧甚至转为爆轰,所引起的爆炸后果及安全事故要远大于只发生燃烧现象的发射药。由此可知,对榴弹主装药的研究意义要高于发射药。因此,进行了含模拟装药的榴弹跌落安全性试验,采用有限元软件模拟了弹体以不同姿态及高度的跌落过程,比较试验与模拟数据,分析了数值模拟方法的可行性,并通过分析DNAN基熔铸炸药受到的应力载荷及加速度过载,提出了跌落冲击对DNAN基熔铸炸药安全性的影响规律。
1 榴弹跌落试验
1.1 试验装置
试验装置如图1所示。包括:MYDL-14压电石英力传感器,灵敏度为4 pC/N,量程为300 kN;示波器;信号放大器;榴弹,材料为45#钢,口径为57 mm,弹头直径为20 mm,弹尾直径为56 mm,高度为225 mm,质量为2.6 kg;底座,材料为钢块;模拟装药,质量为3 kg,直径为56 mm,高度为50 mm;导向装置,材料为PVC管,口径为63 mm,高度为500 mm。

图1 试验装置示意图Fig.1 Schematic diagram of the test device
1.2 试验原理
弹体受到的冲击压力

式中:F为冲击压力,kN;α为力传感器灵敏度系数,pC/N;β为信号放大器的放大倍数,β=1;V为示波器示数,mV。
弹体受到的冲击应力载荷

式中:p为压强,MPa;F为冲击压力,kN;S为受力面积,m2。
1.3 试验方案
鉴于弹体结构强度,将跌落高度设为30 cm和40 cm。在试验过程中,按照选定的高度,选择弹头顶部垂直跌落在力传感器上,并在力传感器底部放置一个钢块,目的是减少由于冲击引起的地面振动以及地面过软带来的缓冲,并应用导向装置控制跌落角度,通过示波器和信号放大器采集数据,做出冲击压力曲线。
1.4 试验结果
图2 为在30 cm和40 cm高度跌落时弹体受到的冲击压力曲线;图3为由式(2)计算得到的弹体受到的冲击应力载荷曲线。

图2 弹体跌落冲击压力曲线Fig.2 Drop impact pressure curve of the projectile
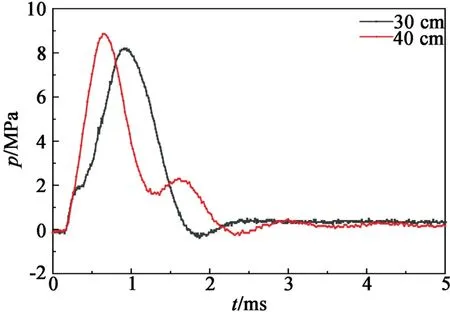
图3 弹体跌落冲击应力载荷曲线Fig.3 Drop impact stress load curve of the projectile
2 弹体跌落数值计算
2.1 建立有限元模型
采用有限元软件中的三维实体,按照实际尺寸1∶1对弹体建模,单位制为mm·t·s,主要包括弹壳、主装药、发射药3个部分,弹体外形和内部装药结构如图4所示。外壳材质为45#钢[8];主装药为DNAN基熔铸炸药[9-11],组分为DNAN/HMX,质量比20∶80,采用双线性本构模型;发射药组分为硝胺、RDX和聚氨酯弹性体,采用黏弹性模型[12];靶板长为2 000 mm,宽为2 000 mm,厚度为750 mm,材质为高强度钢[13]。材料参数如表1所示。

图4 弹体有限元模型与内部装药剖面网格图Fig.4 Finite element model and grid diagram of internal charge section of the projectile

表1 材料参数Tab.1 Material parameters
为增加计算效率,网格属性为六面体结构网格,单元类型为八结点热耦合六面体单元。在模拟跌落过程中,不计算空气阻力,假设弹体跌落为自由落体运动。根据能量守恒定律,可求得弹体在跌落至靶板时的瞬时速度[14]为

式中:v为速度,m/s;g为重力加速度,g=10 m/s2;h为高度,m。
将该瞬时速度设为弹体的临界速度,为节省计算时间,采用初始速度等效跌落高度的方法[15]。
2.2 计算工况
首先,模拟跌落高度为30 cm和40 cm的弹体跌落。对于跌落安全性试验,国外制定了极其严格的标准[16-17];同时,分析在实际跌落过程中跌落姿态对弹体冲击的影响,选取了4个跌落角度。因此,弹体跌落高度设为1.5 m和12.0 m,跌落角度设为30°、45°、60°和90°。
3 仿真结果分析
3.1 试验与模拟对照分析
由图5可知:弹体跌落高度为30 cm时,应力峰值区间为8.1~8.5 MPa;跌落高度为40 cm时,应力峰值区间为8.8~9.0 MPa;试验与模拟应力峰值误差小于10%。含模拟装药的弹体跌落试验的仿真模拟应力载荷曲线的规律及作用时间,与榴弹跌落试验过程中弹体的应力曲线基本相同,证明弹体模型建立正确,同时材料模型参数选择合理。因此,可以采用有限元软件模拟弹药跌落过程,并分析其冲击特性。在此基础上,开展DNAN基熔铸装药榴弹在不同跌落高度、跌落姿态以及弹体内部装药整体升温变化等多种工况的仿真模拟计算,并对其跌落状态安全性进行分析。
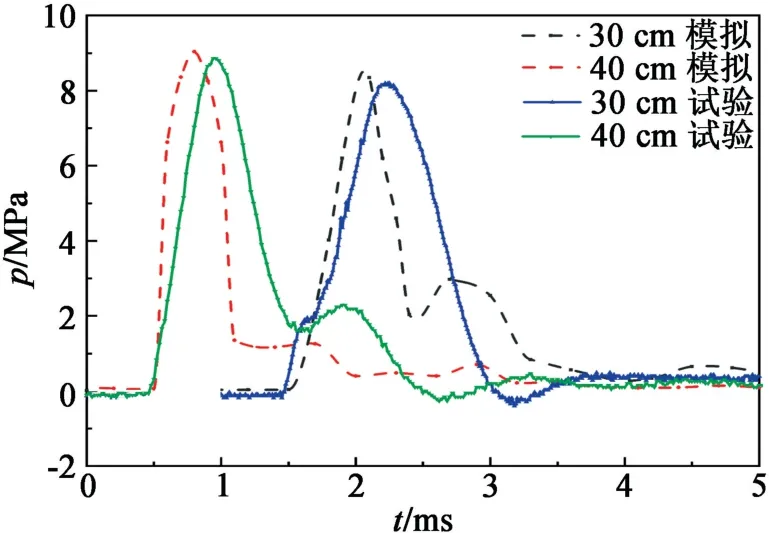
图5 弹体所受应力的模拟与试验结果对照Fig.5 Simulation and experiment comparison of stress on the projectile
3.2 不同跌落高度下DNAN基熔铸炸药冲击载荷分析
为了分析弹药在垂直跌落时的冲击载荷传递规律,在DNAN基熔铸炸药上选取了3个节点。如图6所示,节点1#为弹体装药头部,节点2#为中部,节点3#为尾部。对各节点应力载荷和加速度过载进行分析。

图6 节点位置分布图Fig.6 Distribution of the nodes
3.2.1 弹体在1.5 m高度处跌落
图7 为弹体在1.5 m高度处垂直跌落时DNAN基熔铸炸药受到的应力载荷和冲击加速度过载曲线。由图7可知:弹体在跌落时,应力载荷和加速度过载峰值均在节点1#处达到最大,分别为35.0 MPa和30 000g;在节点3#处最小,分别为26.8 MPa和20 000g。应力载荷作用时间均在节点1#处最大,为1.0 ms;节点3#处最小,为0.9 ms。加速度过载作用时间均在节点1#处最大,为1.7 ms;节点3#处最小,为1.5 ms。

图7 1.5 m跌落时DNAN基熔铸炸药的应力载荷和加速度过载曲线Fig.7 Stress load curves and acceleration overload curves of DNAN-based melt-cast explosive during 1.5 m drop
3.2.2 弹体在12.0 m高度处跌落
图8 为弹体在12.0 m高度处垂直跌落时DNAN基熔铸炸药受到的应力载荷和冲击加速度过载曲线。由图8可知:弹体在跌落过程中,应力载荷和加速度过载峰值均在节点1#处达到最大,分别为85 MPa和73 000g;在节点3#处最小,分别为80 MPa和48 000g。应力载荷作用时间均在节点1#处最大,为1.0 ms;节点3#处最小,为0.9 ms。加速度过载作用时间均在节点1#处最大,为1.9 ms;节点3#处最小,为1.6 ms。
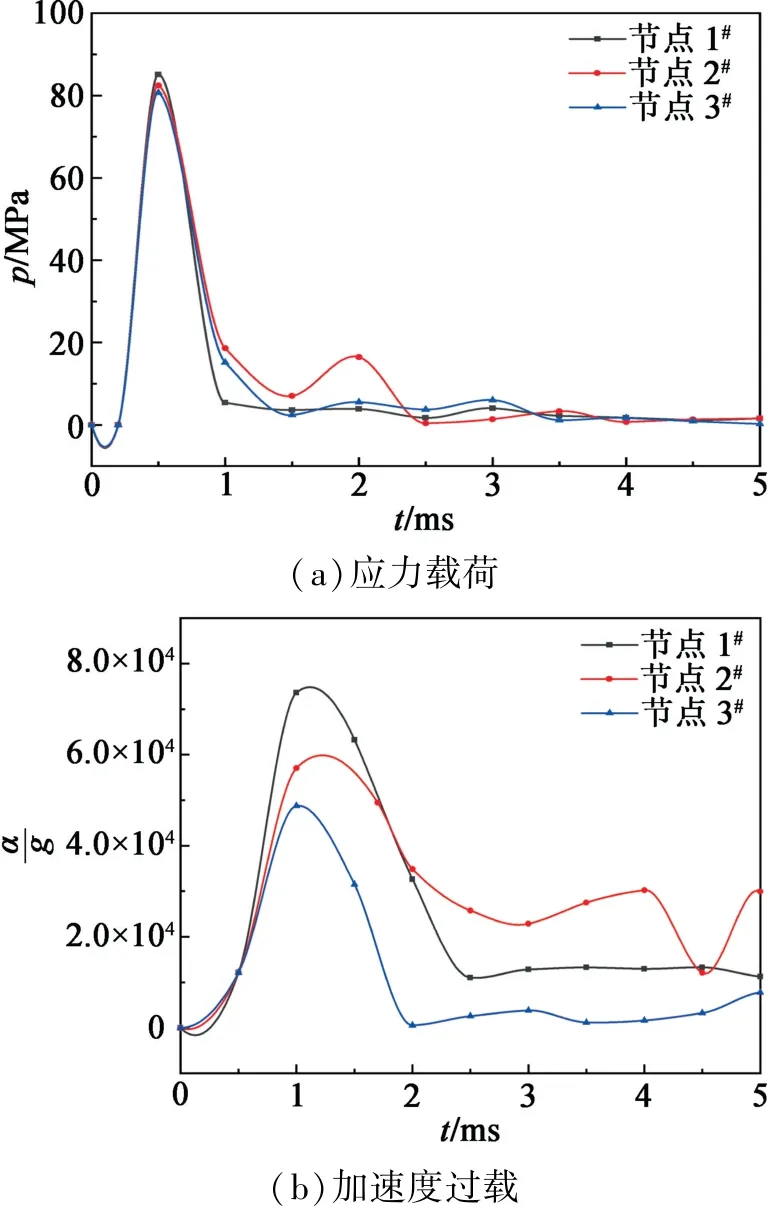
图8 12.0 m跌落时DNAN基熔铸炸药的应力载荷和加速度过载曲线Fig.8 Stress load curves and acceleration overload curves of DNAN-based melt-cast explosive during 12.0 m drop
3.3 不同跌落姿态下DNAN基熔铸炸药冲击载荷分析
由于弹体在较高处跌落时,跌落姿态在空中会发生变动。针对跌落姿态对冲击载荷的影响,在仿真计算时,模拟了弹体在12.0 m高度处以30°、45°、60°和90°的角度跌落的过程,并对DNAN基熔铸炸药在不同角度跌落时节点2#处的应力载荷和加速度过载峰值进行了分析,如图9所示。
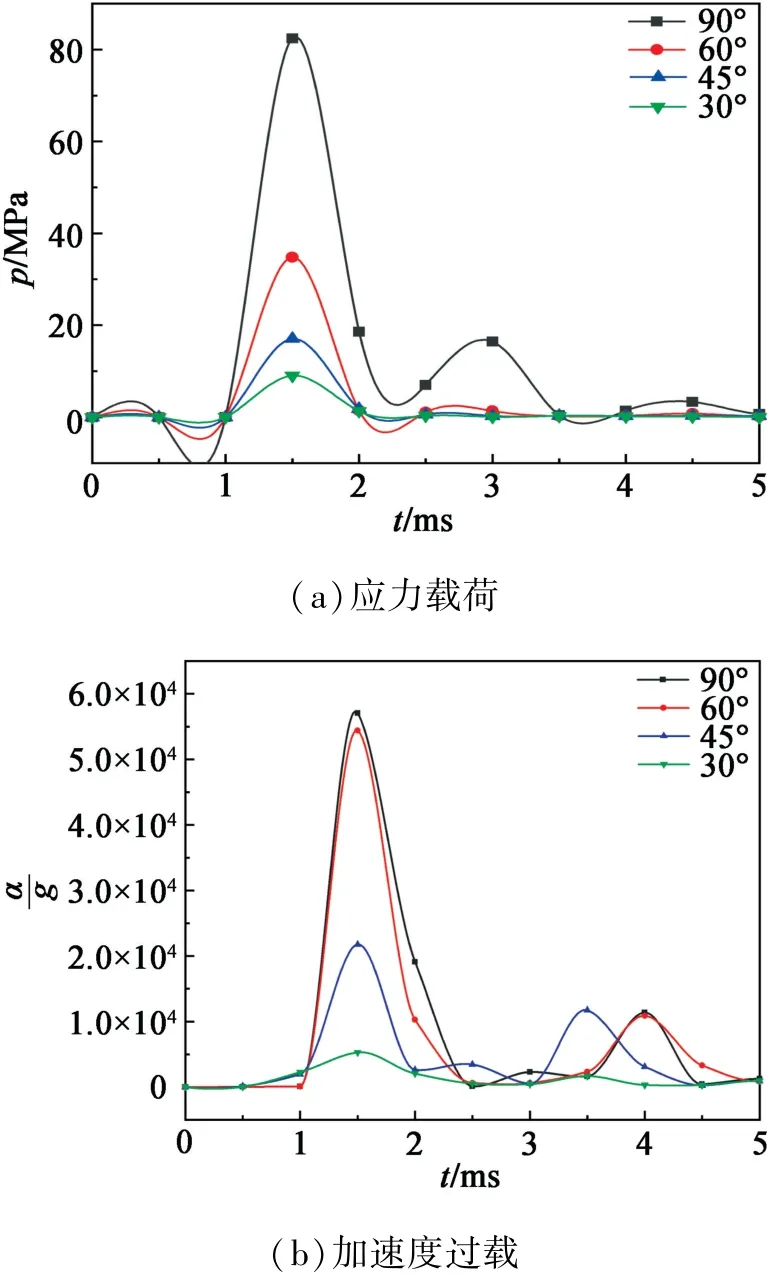
图9 不同跌落姿态下DNAN基熔铸炸药的应力载荷和加速度过载曲线Fig.9 Stress load curves and acceleration overload curves of DNAN-based melt-cast explosive under different drop angles
由图9可知:弹体在12.0 m处跌落时,应力载荷和加速度过载峰值均在90°时最大,分别为81 MPa和57 045g,作用时间约为2.1 ms;在30°时最小,分别为9 MPa和5 271g,作用时间约为2.0 ms。
3.4 不同跌落高度下DNAN基熔铸炸药升温变化
选取下部节点来分析DNAN基熔铸炸药整体升温变化。同时,为了获得弹体装药在更极端跌落高度的升温规律,还研究了跌落高度为20.0、25.0 m和30.0 m时内部装药的升温变化。
由图10可知:在1.5 m时,弹体内部DNAN基熔铸装药整体升温为0.5℃;其余跌落高度(如12.0、20.0、25.0 m及30.0 m)时,整体升温分别为2.3、3.8、4.8℃以及5.8℃。同时也可知,不同跌落高度时DNAN基熔铸装药整体升温速率近似相等,表现出急剧上升趋势,且都在0.5 ms左右出现升温拐点,逐渐趋于平稳。通过图11可知,DNAN基熔铸炸药的升温变化与弹体跌落高度呈线性关系,随着跌落高度的增加,升温也逐渐增大,但增幅不大。

图10 不同跌落高度下DNAN基熔铸炸药的升温变化Fig.10 Temperature rise change of DNAN-based melt-cast explosive under different drop heights

图11 DNAN基熔铸炸药的升温与跌落高度的关系Fig.11 Relationship between temperature rise and drop height of DNAN-based melt-cast explosive
4 结论
通过试验与模拟数据相对比,证明了有限元软件模拟弹体内部装药冲击特性的可行性。
1)由仿真计算可知,当弹体在1.5 m与12.0 m高度处跌落时,DNAN基熔铸炸药装药受冲击力的峰值、作用时间分别是百兆帕与毫秒级,属于典型的含能材料非冲击点火响应特性。同时,获得了冲击加速度过载变化规律。
2)当跌落高度设为12.0 m时,DNAN基熔铸炸药受到的冲击加速度过载峰值随着跌落角度的增加而变大。弹药在垂直跌落时危险性最高,加速度过载峰值为57 045g;在30°跌落时,危险性最小,加速度过载峰值为5 721g。冲击特性作用时间随着高度及角度的增加而变大。
3)在30.0 m高度跌落时,DNAN基熔铸装药榴弹跌落后内部整体升温最大,为5.8℃,不会影响装药安全性。但跌落冲击应力载荷及加速度过载可能会引发含装药缺陷的DNAN基熔铸装药榴弹产生局部热点,导致发生意外爆炸或早炸现象。因此,未来可在此基础上开展DNAN基熔铸装药跌落状态下的细观模型升温规律与点火机制研究。
总之,在进行含DNAN基熔铸装药榴弹跌落安全防护时,应针对上述高过载的情况进行跌落安全性分析,防止DNAN基熔铸炸药的应力载荷及加速度过载超过安全阈值,引起炸药爆炸,造成人员伤亡和财产损失。
