海洋采油平台直流配电网瞬时负载的适应性评估
2021-10-09李昌明闫红华
李昌明,闫红华
(1.电网智能化调度与控制教育部重点实验室(山东大学),山东 济南 250061;2.山东国瑞电力科技有限公司,山东 济南 250003)
0 引言
直流配电技术可摒弃交流海缆无功充电功率较大的弊端[1],利于分布式清洁能源的接入,在技术和经济方面更有优势[2—5],因而直流配电网在海洋采油平台展现出较为良好的应用前景。但海洋采油工程电机类负载直接起动时会导致瞬时的负荷冲击[6—7],可能影响直流配电网运行。
直流配电网对瞬时负载的适应能力,一定程度上可以通过扰动后直流电压的跌落程度来衡量[8]。此电压动态过程可依靠时域仿真获取,但是计算量普遍较大,而且不利于揭示机理规律。另一方面,精确的解析分析将面对非线性高阶微分方程的求解问题,存在一定的困难。
过去几十年,已有学者在瞬时负载的影响方面开展了相关研究,但是大多数仅针对交流电网。文献[9]提出了基于均方根电压水平的电能质量指数,并用于电机起动引起的电压变化评估;文献[10]给出了3个与电机起动相关的图表,以揭示相关电能质量问题的关键因素;文献[11]提出了一种基于黎曼求和原理评估电压下降程度和发电机电流暂态冲击的方法;文献[12]则通过仿真分析了微电网中电机起动电流与电压降之间的关系。
而在直流配电网的受扰后动态分析方面,已有研究构造不同形式的稳定判据以评估动态过程的稳定性。文献[13]总结了柔性直流配电系统稳定分析及控制面临的挑战;文献[14]基于潮流可行解提出电压稳定分析方法;文献[15—16]利用小信号阻抗分析法,借助伯德图和奈奎斯特法评估系统稳定性;文献[17]提出适用于交直流混联配电系统的阻抗匹配稳定性分析方法,确定了阻抗稳定边界;文献[18]则依靠小信号模型的零极点分布评估稳定性。针对大扰动稳定分析,文献[19—20]建立了系统的混合势函数模型,文献[21]则利用李雅普诺夫直接法分析了直流微电网的大扰动稳定性,虽然涉及大扰动稳定性,但其结果通常偏保守,无法准确给出稳定域。
综上所述,目前有关瞬时冲击负载的影响研究主要集中于交流电网,专门针对直流电网的研究较为少见。在动态性能的评估中[22],多是间接构造稳定判据[23]或进行时域仿真,两者均存在一定的问题,如稳定判据较为复杂,时域仿真难于解析。
文中采用简化降阶的思路对系统微分代数方程做一定的合理近似,在不显著影响精度的情况下给出了直流电压动态的解析表达式,直观评估不同瞬时负载情况下直流母线电压的跌落程度,研究了海洋采油平台直流配电网对瞬时负载的适应性。模型仿真验证了解析表达式的正确性。
1 海洋采油平台电机起动特性
在海洋油气开采中,其核心部件为电潜泵、压缩机、注水泵、增压泵等采油设备,多采用大容量异步电动机驱动,负载容量较大,某些负载单机容量甚至可超过1 MW,几种典型的海洋采油平台电机参数如表1所示。

表1 典型电机参数Table 1 Typical motor parameters
上述电机起动时,起动电流远大于额定电流,并吸收大量功率,对系统产生严重的冲击。不同的电机起动方式其冲击情况不同,当采用降压起动、变频起动等软起动方式时,其吸收功率约为额定功率的1~3倍,而当电机采用直接起动时,冲击情况更严重,此时吸收功率可达额定功率的3~7倍。
直流配电网不存在功角稳定性、频率稳定性的问题,影响其性能的主要因素为直流电压稳定性。而直流母线电压受有功功率供需关系影响,电机起动时吸收的无功功率不会直接影响系统的直流电压稳定性,因此文中将以图1所示瞬时负载情况为例分析海洋采油平台直流配电网对瞬时负载的适应性。

图1 瞬时负载的功率波形Fig.1 The power waveform of instantaneous load
2 瞬时冲击下直流配电网电压解析
2.1 直流母线电压解析表达式
海洋采油平台的直流配电网结构通常如图2所示,其通过AC/DC换流器从交流侧获取电力,分别通过DC/AC和DC/DC换流器为交流负载、直流负载供电,并通过换流器接入风电、光伏等新能源发电形式[24]。
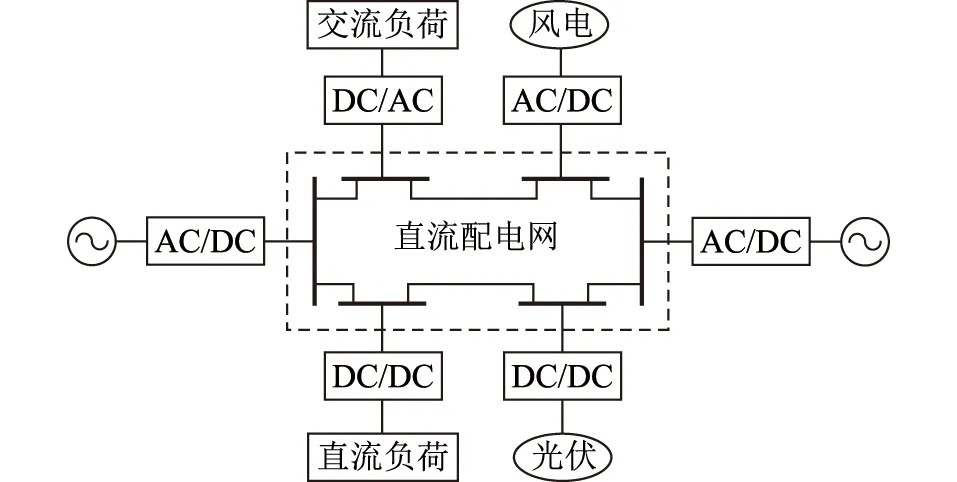
图2 直流配电网结构示意Fig.2 Schematic diagram of DC distribution network


图3 主站直流电压控制框图Fig.3 Control block diagram of master station DC bus voltage
由于电流内环控制的时间常数和测量延时通常远小于系统动态过程和电压外环控制的时间常数,因此文中忽略电流内环的动态过程,认为其瞬时达到控制目标。由图3计算可得:
(1)
因此,交流侧输入的功率为:
(2)
换流站的直流侧等效电路见图4,其中Ceq为换流站等效电容;Rij,Lij,Cij为线路参数;Pdc为换流站向直流侧输出的功率;Pac为交流侧输入功率;电流源iC为交流侧等效电源;iloss为换流站损耗。
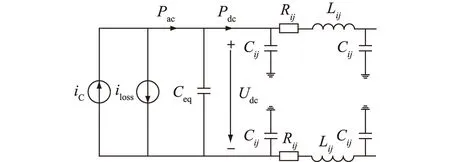
图4 换流站等效电路Fig.4 Equivalent circuit diagram of converter station
通常换流站损耗可忽略。由图4可得,瞬时冲击负载时直流母线电压表达式为:
(3)
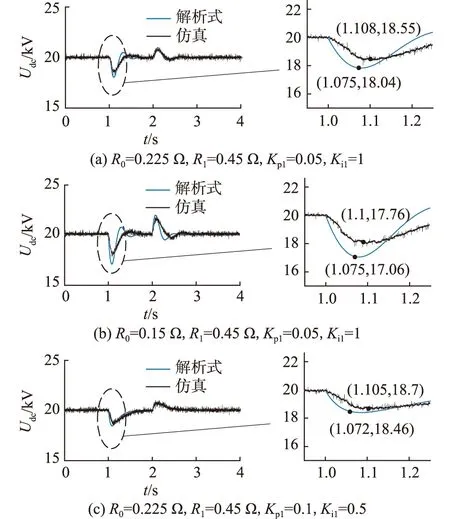
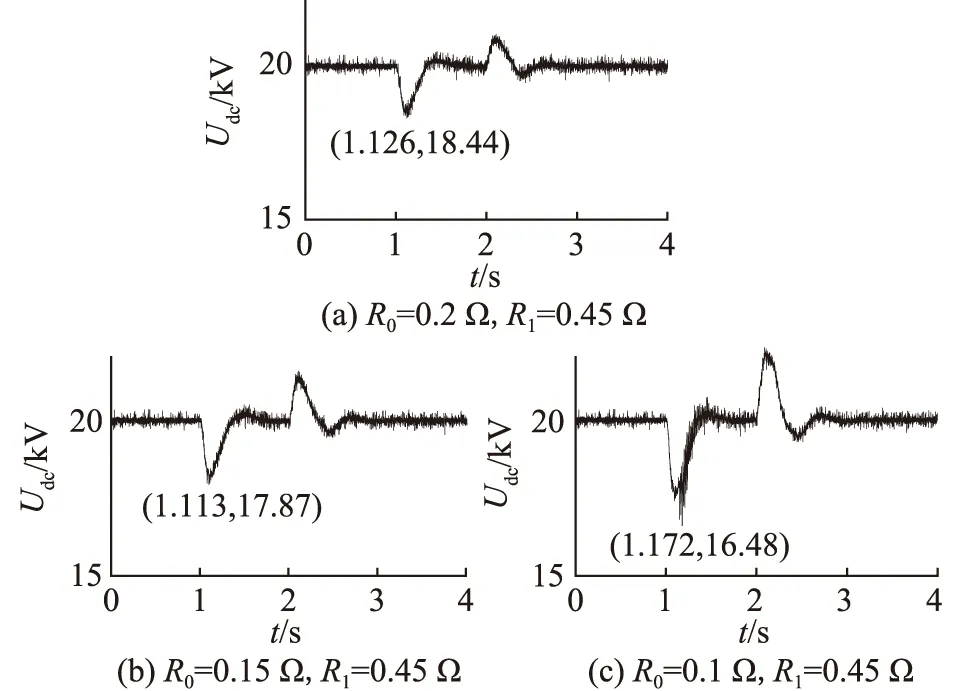
初始时刻,直流电压记为Udc0,在较短时间Δt内,认为dUdc< (4) (5) 其中: (6) 对式(5)进行分析与计算,可得瞬时负载时电压跌落的极限值为: (7) 同上分析,可根据表达式求出瞬时负载结束时的电压及电流,进而求得瞬时负载结束后的直流母线电压表达式,其表达形式与上述表达式类似,不再赘述。 当直流母线电压跌落时,会使调制比增大,可能导致调制波处于过调制区,影响系统的调制。模块化多电平换流器(modular multilevel converter,MMC)型柔性直流与传统直流相比具有不存在换相失败等优点,适合构成多端直流系统[25],具有光明的应用前景,因此文中以此为例分析直流电压跌落对调制的影响。 柔性直流换流器通常采用最近电平逼近调制,其正常工作的调制范围为Udc/2。考虑交流侧接地,换流站的结构如图5所示。 图5 换流站结构Fig.5 Structure of the converter station 其中,SM为桥臂模块;Lac,L0分别为交流侧等效电感及桥臂电感;Usa,Usb,Usc为交流侧电源相电压;Uva,Uvb,Uvc为调制得到的交流侧电压。 在最近电平逼近调制中,三相的上、下桥臂导通的子模块数Npj,Nnj(j为a、b、c三相)为: (8) 为分析最近电平逼近调制工作在过调制区的调制情况,可暂时不考虑桥臂电感的作用[25]。 故正极点P与连接点J(J代表A,B,C三点)的电压UPJ,即上桥臂电压值为: (9) 直流侧正极对地电压可以表示为: (10) 式中:UPA,UPB,UPC分别为a、b、c三相的上桥臂电压;UAG,UBG,UCG分别为a、b、c三相连接点J对地电压。 (11) 所以UPG=NUC/2=Udc/2,可实现良好调制。 图6 调制得到的交流电压波形Fig.6 The approximate modulation waveform of equivalent AC-side voltage 在此情况下,调制出的交流电压包含6k-1次负序谐波分量,6k+1次正序谐波分量,因此会产生6k-1次电流负序谐波分量,6k+1次电流正序谐波分量,进而产生6k次谐波功率波动,造成直流母线电压产生6k次谐波,而在交流侧又调制出6k-1次负序谐波分量,6k+1次正序谐波分量。 当直流侧负载突增时,直流侧吸收功率快速增加,Pdc>Pac,导致直流母线电压下降。 根据式(7)可得,瞬时负载时直流母线电压极限值Udcmin与主站PI控制参数及瞬时负载的定性关系如图7所示。 图7 直流电压极限值Udcmin与不同参数的关系Fig.7 The relationship between Udcmin and different parameters 由图7(a)、图7(b)可以看出随着Kp1,Ki1的减小,直流电压极限值Udcmin减小,电压跌落程度增大,海洋石油直流配电网对瞬时负载的适应性变差,直流系统的控制会影响海洋石油直流配电网对瞬时负载的承受能力。 而不同电机参数及不同的电机起动方式会影响到瞬时负载的大小,由图7(c)可以看出,当瞬时负载增大时,直流母线电压跌落加深,海洋采油平台的适应性变差。同时,随着直流电压的降低,调制出的交流电压不再是良好的正弦波,而将包含大量的6k-1次负序谐波分量和6k+1次正序谐波分量。 建立如图8所示的四端柔性直流配电网仿真模型。交流侧额定电压为10 kV,两侧交流系统通过基于钳位双子模块的MMC与直流线路相连,换流器电平数为11。MMC1模拟直流配电网的主站,采用定直流电压及无功功率的控制方式,直流电压为20 kV,交流侧吸收的无功功率为0 Mvar。MMC2采用定有功功率及无功功率的控制方式,交流侧吸收有功功率为5 MW,无功功率为0 Mvar。光伏利用最大功率点跟踪控制输出5 MW的功率。直流负载处采用定负载直流电压控制方法,保持负载处电压为0.75 kV。 图8 四端柔直配电系统结构Fig.8 The system structure of a four terminal DC distribution network 文中通过改变电阻来模拟电机起动时产生的瞬时有功冲击负荷现象,1 s时在负载侧并联电阻R0,持续时间为1 s,此后电阻变为R1。通过比较仿真与解析式计算得到直流母线电压波形,验证了解析式的正确性。比较不同仿真情况下的电压跌落程度,验证了2.3节利用解析式得到的直流母线电压跌落与控制参数及瞬时负载值之间的关系,进一步验证了文中所提解析表达式可以反映直流配电网对瞬时负载的适应性这一观点。 设置不同的控制参数及不同的瞬时负载进行仿真,并利用求得的解析表达式进行计算,得到不同情况下Udc的波形,如图9所示。 图9 直流母线电压波形对比验证Fig.9 The comparison validation of DC bus voltage waveforms 由图9可知,通过解析式得到的波形与仿真得到的波形近似一致,经计算三者最大误差分别为2.75%,3.94%,1.28%,误差在可接受范围内,可以得出文中推导的解析表达式是正确的。 使瞬时负载保持在R0=0.125 Ω,R1=0.25 Ω,对主站PI控制环节设置不同的控制参数进行仿真,记录其Udc的仿真波形见图10。由图10可知,1 s时,Udc先降低,而后逐渐上升,存在一个最小值。通过图10(a)、(b)和(c)的对比分析,可以看出当瞬时负载情况确定时,随着控制参数Kp1,Ki1的减小,电压最小值减小,直流母线电压跌落增大,海洋采油平台对瞬时负载的适应性变差。 图10 不同PI控制参数模拟下直流母线电压波形Fig.10 The DC bus voltage waveforms under different PI control parameters simulation 控制参数不变,通过保持并联电阻倍数相同而瞬时负载结束后电阻值不同,近似模拟不同电机参数、相同起动方式下的电机起动瞬时有功负荷,得到不同瞬时负载时的直流母线电压波形,见图11。 图11 不同电机参数模拟下直流母线电压波形Fig.11 The DC bus voltage waveforms under different motor parameters simulation 由图11可知,瞬时负载导致Udc跌落,而且当主站PI控制参数确定时,随着并联电阻的减小,直流母线电压跌落增大,即电机容量越大,电机起动时吸收功率越多,海洋采油平台直流配电网的适应性越差。 保持控制参数不变,通过使瞬时负载结束后的并联电阻值相同,瞬时负载时的并联电阻值不同来近似模拟相同电机参数、不同起动方式下的电机起动瞬时有功负荷,可得到瞬时负载结束后负载相同而瞬时负载值不同时的直流母线电压波形,如图12所示,可以近似反映不同电机起动方式时的系统运行情况。 图12 不同电机起动方式模拟下直流母线电压波形Fig.12 The DC bus voltage waveforms under different motor starting modes simulation 由图12可知,随着瞬时电阻R0的减小,直流母线电压跌落增大,即电机起动时吸收功率越大,电压跌落越大,此起动方式下直流配电网对电机负载起动的适应性越差。 为验证直流电压跌落时的调制情况,对图11(b)所对应的模型进行仿真,得到交流侧电压仿真波形如图13所示。 图13 系统仿真波形Fig.13 The waveforms of simulation 由图13可知,当直流电压跌落使调制波超出调制范围时,交流侧电压不再为正弦波,此时交流电压的6k-1和6k+1次谐波分量显著增加。由此可以看出,瞬时有功负载会影响海洋采油平台直流配电网的电能质量,导致系统交流侧产生大量谐波。 文中针对海洋石油工程电机起动时的瞬时冲击负载,通过简化降阶推导瞬时负载时直流母线电压的解析表达式,得出以下结论: (1)通过仿真验证可得通过文中推导的解析表达式与仿真得到的波形差异在误差可接受范围内,文中的解析表达式可以有效反映瞬时负载时电压跌落情况。 (2)通过解析式可得,海洋采油平台直流配电网主站的控制参数会影响其对瞬时负载的适应性,随着PI控制参数的减小,其对瞬时负载的适应性变差。此外,不同电机参数及不同电机起动方式也会影响其适应性,电机起动时瞬时负载越大,海洋采油平台的直流母线电压跌落越大,适应性越差。 (3)海洋采油平台直流配电网直流电压的跌落易导致调制波超出调制范围,影响调制波的调制,使系统电能质量变差。 文中仅分析了电机起动时产生的瞬时有功负荷,未来可进一步研究瞬时无功负荷对海洋石油直流配电网的冲击及对自身起动情况的影响。 本文得到中海石油(中国)有限公司北京研究中心科技项目(CCL2019RCPS0268RSN)资助,谨此致谢!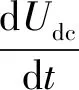

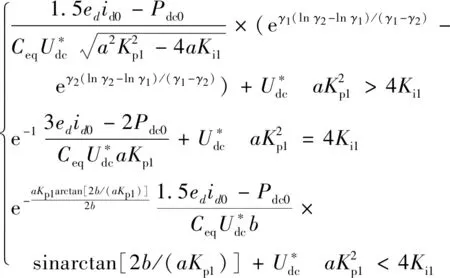
2.2 系统调制分析




2.3 瞬时负载对直流配电网的影响

3 案例仿真

3.1 解析表达式验证
3.2 不同主站PI控制参数下瞬时负载仿真分析

3.3 不同瞬时负载下仿真分析


4 结论
