反应堆压力容器C形密封环多因素作用下的密封可靠性研究
2021-10-09董元元李玉光
董元元 罗 英 李玉光 胡 甜
(核反应堆系统设计技术重点实验室,中国核动力研究设计院,四川 成都 610213)
0 引言
反应堆压力容器(简称RPV)通常由顶盖组件、筒体组件和紧固密封件组成,其密封结构是一种典型的静密封结构,通过紧固螺栓施加预紧力使密封环产生初始密封,依靠密封环的回弹性能保证服役过程中的密封可靠性。因此,密封环的密封性能的可靠性对于RPV的密封性和完整性至关重要。
目前,国内外RPV常用的密封环有O形密封环和C形密封环两种。C形密封环(简称C形环)由于其更优异的密封性能而大量使用于国内核电站中,前期通过国产化研制获得了大量的试验数据[1,2],同时也逐渐形成了数值计算方法并开展了模拟研究[3-6]。但是,由于C形环结构复杂,会引入较多的敏感因素对密封性能产生影响。本文旨在针对C形环密封性能的多个影响因素进行分析,获得C形环在多因素作用下的密封可靠性和各影响因素的可靠性灵敏度,为C形环的设计及工艺控制提供参考和指导。
1 密封可靠性数值计算方法
1.1 C形密封环结构
C形环由3层结构组成,即内层弹簧基体、中间层金属覆面和外层银层,中间层和银层均为外侧开口。弹簧基体是由Inconel X750弹簧丝材螺旋密绕而成的环状结构,保证了密封环的回弹量和密封比压;中间层金属覆面是由Inconel 600板材形成的管套状结构,其主要作用是包覆弹簧基体,防止银受压后挤入弹簧间隙;外层银层采用纯银包覆在金属覆面上,银层受压产生塑性流动,填补密封面上的微观不足,形成有效密封。
由于C形环结构相对复杂,其密封性能将面临多个敏感因素的共同作用,并且这些敏感因素在一定的公差范围内随机分布,这将对C形环的密封性能造成不确定的影响。下面将借助ANSYS的概率分析功能[7]对C形环密封可靠性进行分析。
1.2 密封可靠性分析模型
利用ANSYS概率分析功能进行密封可靠性分析的主要步骤为:生成分析文件、可靠性分析、结果后处理。
1.2.1 生成分析文件
建立如图1所示的“C形环—法兰”结构的有限元分析模型,其中C形环结构能够反映出其截面直径、弹簧丝材直径及包覆层厚度等特点;下法兰为带密封沟槽的结构,通过控制沟槽的深度hdep来限制C形环压缩量的大小。
通过对上法兰顶部施加轴向压缩载荷来实现对C形环的压缩和回弹,计算过程分为“加载压缩→回弹至临界点→完全回弹”三步。加载压缩到位后C形环的压缩量为δ=d-hdep,而C形环与上法兰密封面接触区域的线载荷即为工作点线载荷f0。回弹至临界点状态,即将压缩载荷减小至回弹过程初始泄漏点的状态(取此时的密封载荷f2=46 N/mm[4]),给出对应的C形环变形量即可求得有效回弹量。完全回弹过程中,将压缩载荷减小至足够小(本文为保证计算收敛性,取该载荷为4 N/mm),并将该状态点作为完全回弹状态以计算总回弹量。
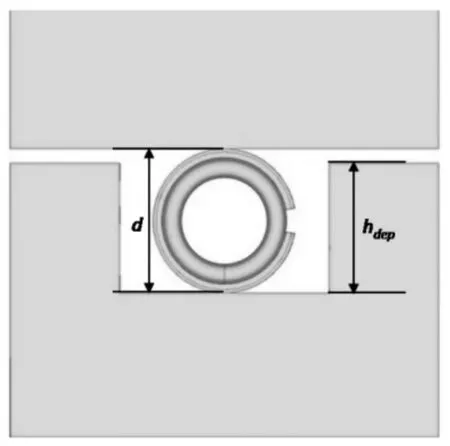
图1 可靠性分析模型
1.2.2 可靠性分析设置
可靠性分析的相关设置主要包括选择输入变量、指定输出结果变量和确定分析工具及方法。
C形环尺寸公差及压缩量取值范围是关注的重点。由前期研究[4]可知,C形环直径D和银层厚度Th2对密封特性影响较小;因此本文所研究的敏感因素,即输入变量包括弹簧截面直径Dspr、弹簧丝材直径Drod、中间层厚度Th1和压缩量δ。
由于上述输入变量均是独立随机变化的,故可认为服从高斯分布。在随机事件中,当取值概率小于5%时,即称之为小概率事件,为了使输入变量的随机取值在其公差范围内的概率不小于95%,则高斯分布中的期望值和标准差的取值应满足“2Σ原则”。根据C形环的实际设计值,各输入变量的具体参数如表1所示。

表1 输入变量分布类型及参数
C形环的密封可靠性可以通过密封载荷及回弹量进行表征,故在分析中的结果输出变量指定为总回弹量Δt,有效回弹量Δe和工作点线载荷f0。C形环的实际设计要求[2]为Δt>0.25mm,Δe>0.2mm;工作点线载荷应与密封面的硬度相匹配,本文取760N/mm<f0<820 N/mm。
ANSYS所提供的结构可靠性分析功能中,常用的分析方法有蒙特卡洛法和面响应法,本文采用蒙特卡洛法进行研究分析,抽样方法选用拉丁超立方法,抽样次数为50次。
2 密封可靠性计算结果
通过循环执行分析文件,可以得到可靠性分析数据库,包括每次抽样的输入变量和输出结果变量,以及各变量的平均值、标准差和最值。根据可靠性分析数据库中的结果,可以得到输入变量的抽样情况,见表2。δ、Dspr、Drod和Th1的抽样结果的与输入参数基本一致,并且抽样结果在公差范围内的概率均大于95%。上述结果说明抽样过程是可信的,抽样结果满足要求。
根据可靠性分析数据库,可以得到Δt、Δe和f0三个输出变量的平均值随抽样次数的变化情况,模拟次数取为50次时,基本可以保证计算结果的收敛性。经过50次抽样计算后,Δt的平均值为0.419 mm,Δe的平均值为0.350 mm,f0的平均值为792.0 N/mm。
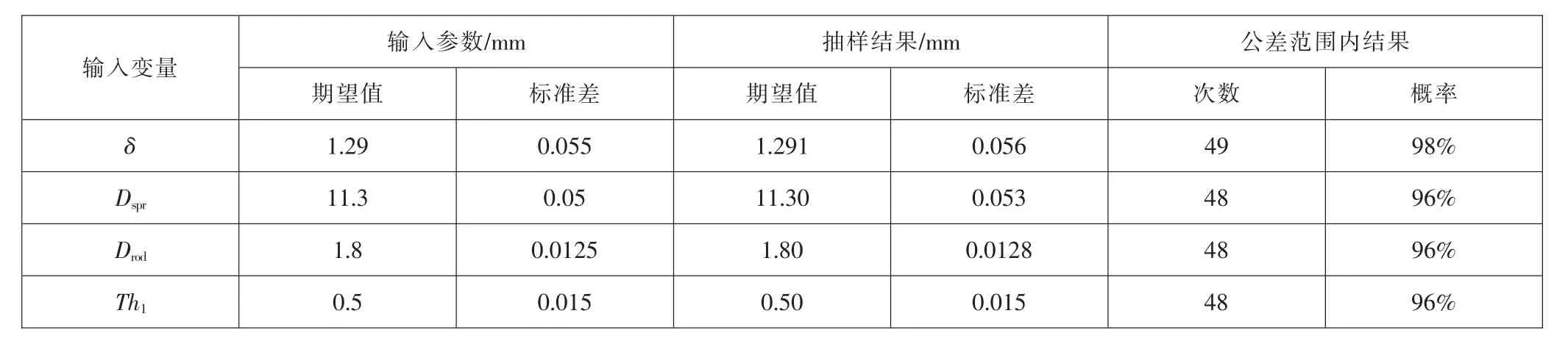
表2 输入变量抽样情况
3 C形环密封可靠性分析
3.1 密封可靠性
Δt、Δe和f0三个输出结果变量的积分概率分布曲线如图2所示,其积分概率分布曲线具有一定的波动性,这是由于问题本身具有强烈非线性特点,并且抽样样本量不够大所致。
由图2可得,Δt>0.25 mm的概率为100%;Δe>0.20 mm的概率为100%,760 N/mm<f0<820 N/mm的概率为100%。这说明当C形环的结构尺寸及压缩量在公差范围内变化时,C形环的密封可靠性可以得到保证。
3.2 影响因素灵敏度
为了表征四个输入变量对C形环密封可靠性的灵敏度,进行了灵敏度分析,给出如表3所示的相关性系数矩阵。表3中数据的绝对值大小表征了输入变量对输出变量的灵敏度的大小,即影响程度;数据的正负号表征影响的效果,正值表示呈正相关,负值表示呈负相关。
由表3结果可知,在四个输入变量中,压缩量δ、弹簧截面直径Dspr和弹簧丝材直径Drod对密封可靠性的灵敏度较大,而中间层厚度Th1的灵敏度相对较小。从各影响因素的灵敏度正负相关性来看,弹簧截面直径Dspr越大,结构的整体刚度越小,但弹性越好,因此有利于回弹量,但密封载荷越小;弹簧丝材直径Drod越大,整体刚度越大,因此密封载荷越大,但不利于回弹。
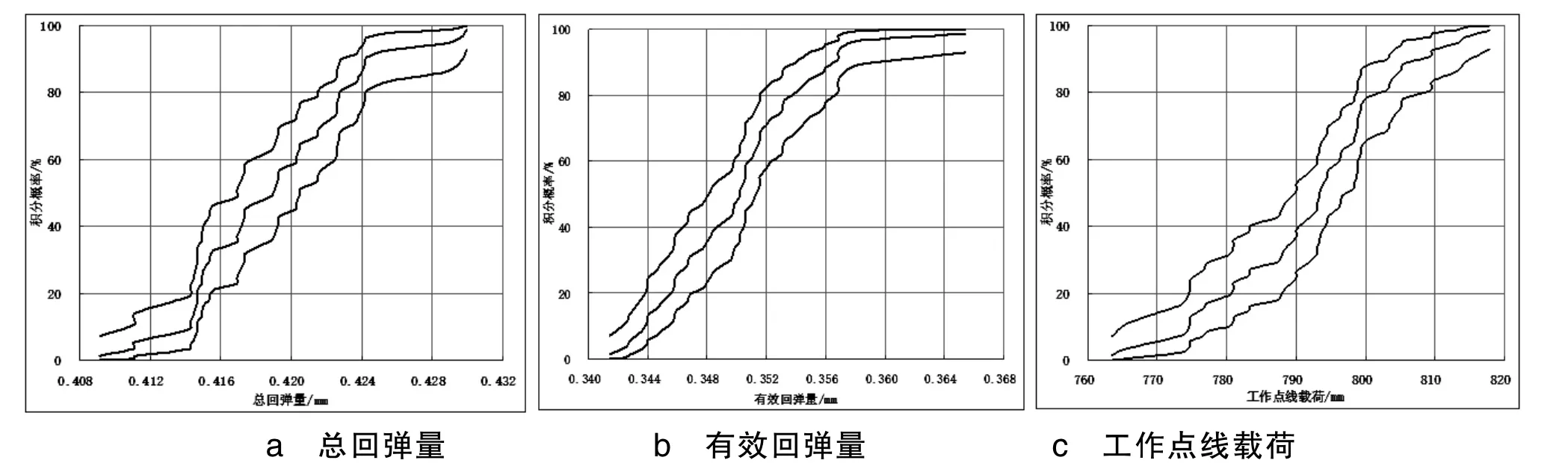
图2 输出变量可靠性分布曲线

表3 输入变量与输出变量的相关性系数矩阵
4 结论
本文针对多个影响因素作用下的C形环进行密封可靠性分析,影响因素包括弹簧截面直径Dspr、弹簧丝材直径Drod、中间层厚度Th1和压缩量δ,通过对总回弹量Δt、有效回弹量Δe和工作点线载荷f0三个输出结果变量进行分析,可以得到:
(1)当四个影响因素在设计公差范围内随机变化时,三个输出变量均满足设计要求,从而验证了目前C形环的设计是合理的;
(2)对C形环密封可靠性,δ、Dspr和Drod的灵敏度较大,而Th1的灵敏度相对较小,因此在C形环的设计与制造中应更加严格地控制C形环的弹簧截面直径、弹簧丝材直径与密封沟槽深度,而对中间层厚度的控制则可相对宽松。
