指向深度学习的单元复习课教学探究

摘要：指向深度学习的数学复习课教学是发展学生核心素养的重要载体。我们可以从一下四个步进行：利用开放性问题，建立知识体系;利用关联研究，强化知识结构;利用变式拓展，实现思维提升;利用整合归纳，优化思维品质。

关键词：一次函数的复习;深度学习;核心素养

深度学习理论参照了布卢姆对认知过程的划分，将理解、记忆、领会归属于浅层学习，发展指向低阶思维;分析、评价、创造归属于深度学习，发展指向高阶思维。可见，教师在平时教学中应加强对学生深度学习能力的培养，以提升学生的学习思维能力。那么，如何开展引领学生深度学习的教学呢？笔者以浙教版教材八年级上册第五章 “一次函数复习”为例，谈谈指向深度学习的教学策略。

1.教学分析

本节课复习的是一次函数的内容，教学中以一次函数y=-x+1的图像串起一节课，由于函数的关联知识多又杂，基础知识模块也多，如果采取知识点点过关，基础模块每块练习，这就变成了炒剩饭+题海的复习课了。这与深度学习的教学理念是背道而驰的，那么我们怎么把单元复习课上活？本节课采取一图以贯之，涵盖多个基础模块，动点问题、等腰三角形的构造、折叠问题，不尽巩固了知识模块，而且将知识模块拉线成网，在问题解决过程中实现知识和思想方法的双重提升，以期指向深度学习。

2.教学过程

2.1利用开放性问题，建立知识体系

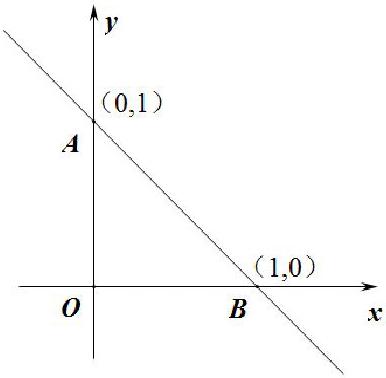
问题1. 从图中你能发现哪些信息？

教学说明：引导学生回顾一次函数的图像和性质，以学定教，变“教学”为“导学”，建立由“形”想“數”的联系。解决这个问题的角度是开放的，可能存在多种不同甚至意想不到的答案，学生可以发现：（1）这是一个一次函数图像，k<0，b>0;（2）用待定系数法，设y=kx+b，代入（1，0），（0，1），列方程组，解出k和b的值，回代入函数解析式，函数解析式是y=-x+1;（3）经过一、二、四象限， y随x的增大而减小;（4）当x满足什么条件时，y=0？y>0？y>1？;当，求y的取值范围;以“当x满足什么条件时，y>0？”教学示范：方法一，当y=0时，x=1，减函数y随x的增大而减小，x<1;方法二，通过观察函数图象y>0是在x轴的上方的函数图象（学生到黑板上演示），这段图象上的点对应的横坐标的范围是x<1;方法三，列不等式，-x+1>0可解出x<1。增减性、图象法、列不等式三种方法可解决已知y范围求x范围和已知x范围求y范围一类问题。基础弱一点的学生能够说出一种方法，能力较强的学生能够说出两种及以上的方法，能够说出全部方法的学生说明对函数的关联知识掌握较好。通过这三种方法的研究，我们发现不等式、方程与函数之间的内在联系，这就是数形结合的奥妙所在。（5）△ABO的面积、周长。基于以上结论形成一次函数的知识结构。这正是了解学生数学水平、透视学生基础知识掌握情况、评价学生思维层次的好机会。

2.2 利用关联研究，强化知识结构

问题2 求经过△ABO的某一个顶点，且平分三角形面积的直线解析式。

教学说明：可以让学生先做，巡视全班发现大部分学生都养成了作图的好习惯，能够直观地反应问题所在。其实把平分三角形面积的直线画出来就成功一步了，师：求函数解析式用什么方法？生：待定系数法。师：一次函数图象需要几个点？生：两个点。师：一个点已经确定，那么关键突破口在哪里？生：第二个点的寻找就成为这道题的解决要点。追问：还有没有其他依据来画这条直线？当然其中还与三角形中线的作用的重要知识点进行转化。这样的追问使学生感悟函数与几何知识的联系，新知与旧知的联系，数学知识是一个体系。反思：求一次函数解析式要注意什么？生：找两个点，用待定系数法。师：找点的方法不同，决定了题目的难易度。

问题3. 点M（a，0）是x轴上的一个动点，

（1）若△ABM为等腰三角形，求点M坐标。

（2）若△ABM为直角三角形，求点M坐标。

（3）若△ABM为锐角、钝角三角形，分别求出a的取值范围。

教学说明：该题的三个问题形似神不似，由于不同的三角形有着不同的性质，因此依据的分类点不同，采用的方法不同。等腰三角形的分类是以相等线段进行分类，按腰分，或者按底边分。那么就要借助圆规来寻找相等线段，采用“两圆一线”方法构造等腰三角形，且运用中垂线的性质定理的逆定理，加强了知识点间的联系。追问：第二问直角三角形根据什么进行分类？学生很快就会采取做已知直线的垂线的方法构造直角三角形，运用等腰直角三角形的性质解题。在讲解这道题时一定要抓住学生分类依据的追问，“你的分类依据是什么？”，分类依据是图形的专属特征，加强了对学生分析问题提取关键信息能力的训练。第三问是从特殊到一般的一个过程，当第二问构成直角三角形的特殊点确定后，x轴被分成了几部分，每一部分就是一般三角形的情况。（1）为（2）方法铺垫，（2）为（3）深浅铺垫，起到思维启示作用。 深入追问，促使学生深层次分析问题，培养学生高阶思维能力。

问题4 在直线 AB上有一动点P，使△POB是等腰三角形，直接写出点P的坐标。

教学说明：经过问题3的探究，对这道题的解决有所启发，学生会对等腰三角形的情况进行分类讨论，以OB为底或者OB为腰，对于中等学生这种分法能够被理解，但是按腰分的时候会漏了情况没有考虑，根据学情，发现按顶角分类更能够被中等学生接受且不会漏写。找到点P后，求出对应的坐标是这道题的第二个难点。追问“如何求出坐标？”，构造直角三角形根据勾股定理求边长，是“以形解数”的一个过程。反思：根据题目条件找到点后求点坐标的关键在于求出点到x轴、y轴的距离。

2.3 利用变式拓展，实现思维提升

问题5 将直线 AB沿某条直线对折，使直线 AB与x轴重合，求该直线的解析式。

教学说明：该题有一定难度，难点一在于学生无法想象如何折叠才能与x轴重合，教学中学生可以让学生动手折一折去发现折痕，是有利于培养同学们动手和实践操作能力的，折出来以后把折线画在图中，将数学问题转化成可操作问题，又回归到数学问题。难点二学生会忽略了第二种折法。如果学生只有一种折法，可以让学生小组讨论一下，互助互学。难点三找到对称轴后不知如何写出函数解析式，引导学生回忆写出这个函数解析式的方法是什么？待定系数法需要什么？那么我们现在需要找出什么就能用待定系数法写出函数解析式了呢？用追问的方式引导学生去求出两个点的坐标。如何求点坐标呢？点坐标就是求出点与x轴、y轴的垂线段的长。求线段的长就可以转化成求几何图形的边长来求解。设元根据勾股定理建立方程，另一种是引导学生发现其中的等腰直角三角形，根据其三边的关系求出点坐标。本题考察的知识点较多，对称轴的性质，等腰直角三角形的性质，渗透转化思想、方程思想、数形结合思想，培养了学生的綜合素质。在教学过程中一定要放手让学生自己去研究，教师根据学生卡在哪里，进行适当的引导，不能够卡住了就告诉学生怎么做。厘清教师和学生谁是主导者，切记不要上成满堂灌的形式。

2.4 利用整合归纳，优化思维品质

师：本节课同学们都学习了哪些数学知识和数学思想方法？

生1：求一次函数解析式需要两个点，用待定系数法。

生2：特殊三角形存在性问题需要根据三角形的特征进行分类。

生：能具体说一说吗？

生2：等腰三角形可以按腰分类或者按底边分类，再者可以按顶角分类，而直角三角形按直角进行分类。

师：讲得非常详细。所以其中渗透了什么数学思想呢？

生2：分类讨论思想

生3：函数图像求点坐标，可以先求出一个坐标，再带入函数解析式求出另一个坐标，这是以形解数。

师：什么数学思想呢？

生3：数形结合思想。

生4：我们还学习用方程思想来求线段长度，其他不知道了。

生5：转化思想

师：大家归纳得非常好。老师用思维导图把你们的归纳进行了整合。

3 几点思考

3.1 聚焦问题的变式过程

本节课打破了常规讲题复习的机械复习课方式，把课堂还给学生，以一个一次函数图像串联起整节课，让学生经历一次函数与三角形知识、动点问题、折叠问题三大问题的过程，深入学习函数与方程、函数与不等式、函数与几何图形的知识。通过这一节课的学习，学生能够深刻领悟到这其中的美妙。方程、数形结合、化归、分类思想的渗透，“两圆一线”方法构造等腰三角形、“动中找静”解决动点问题、类比等方法的再运用，知识点覆盖广泛为这节复习课锦上添花，有利于构建知识网络。总而言之，本节课的设计注重一次函数知识的关联。

3.2 选好知识的生长形式

除了已学习过的的定义、图像、性质外，还有在新授课、习题课中的某些后续学习、对解决问题有帮助的基本模块，例如“两圆一线”方法构造等腰三角形;方程思想求线段长度。在复习过程中将这些模块聚集到一起，结成一个知识网络，知识才能通过复习课得到生长。板书设计也能够彰显知识的生长过程，也是一种行之有效的方法帮助知识点的生长。

3.3 关注个体的素养提升

深度学习是内源性的学习，只有让学生主动地多参与课堂教学活动，这种自主性学习才有可能是有深的。数学深度学习是一个要教师引领的过程，需要教师创设问题、提供机会，引导学生进行探究，从而实现学生深度构建数学认知。

作为数学教育工作者，应该创设有特色的课堂结构，加强深度教学，把这种教学方式进行实践，使深度学习成为学生的学习品质，帮助学生提高学习能力与思维能力，从而切实提升学生的数学核心素养。清醒地分析、诊断学生出现的困惑和问题，学习中的困难和风险，实现立德树人的根本任务。

参考文献

[1]吴永军.关于深度学习的再认识[J].课程·教材·教法， 2019，39（2）：51-58，36.

[2]陈建国.指向深度学习的教学策略探究——以“一次函数的图像”（第1课时）为例[J].中学数学教学参考，2020（6）： 30-32.

作者简介：徐能 性别女，出生年月：1989.11，籍贯江西上饶，研究方向初中数学教育，一级教师，邮编334100。