一类典型磁力摆的全局动力学行为分析*

秦波 尚慧琳 蒋慧敏

(上海应用技术大学机械工程学院,上海 201418)

考虑一类等边三角形排布的典型磁力摆,基于对其全局动力学行为的分析,研究初值敏感性现象及其机制.首先,考虑磁铁位置可以移动,利用牛顿第二定律建立该磁力摆动力学模型.进而,分析不同的磁铁位置所对应的平衡点个数及其稳定性.在此基础上,数值模拟初值敏感性现象和不动点吸引域随磁铁位置移动的演变规律.最后,通过实验验证该现象.研究发现,该类磁力摆普遍存在着多吸引子共存现象,其初值敏感性可归因于其不动点吸引域的分形,其中各不动点位置与磁铁中心投影到磁铁所在平面上的位置并不重合,而是存在微小的偏差;当摆球位置可投影到3 个磁铁对应的等边三角形的形心时,3 个吸引子的吸引域尺寸相当,呈中心对称状且分形,因此初值敏感性现象很明显;移动磁铁位置会直接影响到各吸引域的形态,即离摆球平衡位置投影点近的磁铁对摆球影响最大,离该位置最近的吸引子吸引域会明显变大,而其他吸引子的吸引域则会被侵蚀消减.本文的研究在磁力摆装置设计方面具有一定的应用价值.

1 引 言

单摆是最简单的和最丰富的物理系统之一[1].其中典型磁力摆作为常见的物理实验装置[2,3],通常由一个摆球和若干个永磁铁组成,摆球通过吊线固定,永磁铁则放置在底座上,以磁力作用在摆球上[4,5].同时,磁力摆系统也代表了一类含多共存吸引子现象的系统,对含多共存吸引子现象的系统研究也是学者们研究的热点问题.Marino 和Marin[6]通过实验研究高精度光力学谐振器中由辐射压力和光热效应引起的多时间尺度动力学,阐明该系统存在多共存吸引子现象.杨科利[7]研究了耦合不连续系统的同步转换过程中的动力学行为,通过计算耦合不连续系统的同步序参量和最大李雅普诺夫指数随耦合强度的变化,发现两类周期吸引子和同步吸引子同时存在,系统表现出对初值敏感的多共存吸引子现象.Zhang 等[8]在Hopfield 神经网络中引入非理想磁通控制的忆阻器模型,构造了一种具有多个双涡卷吸引子的新型忆阻模型,利用理论分析和数值模拟观察到该系统多共存吸引子现象.Lai 等[9,10]提出一类新的混沌系统,利用数值模拟和实验阐明该类系统具有无穷多的平衡点和多共存吸引子现象.

同时,磁力摆代表了一类具有非线性特性和不可预测性的有趣物理系统,其表现出的物理现象和背后的动力学行为研究一直是学者们关注的热点.Sanz[11]通过将磁力摆系统的3 个永磁铁设计为电磁,并在电磁铁放置基面上设置超声波传感器来测量摆球运动的位置,设计了一种具有多变量、非线性和混沌过程控制的实验装置,可用于非线性系统的相关控制研究.Kraftmakher[12]设计了一种将两块永磁铁放置在一根薄的铝棒上,并设置旋转运动传感器组装的磁控摆实验装置系统,得出该系统可用于研究非线性振荡和混沌运动,改变摆球的设计参数可使实验适用范围更广.Wijata 等[13]设计了一种单摆在一定角度范围内摆动,下方放置一块永磁铁的磁力摆实验装置系统,通过数值模拟和实验研究发现,该单磁摆单侧振荡具有不同的周期.Motter 等[14]对3 个永磁铁呈等边三角形排布的磁力摆装置进行了数值模拟和实验研究,提出该磁力摆系统摆球不规则运动受瞬态混沌鞍[15]的瞬态相互作用的控制,认为是瞬态混沌现象[16−18].Khomeriki[19]设计了一种具有磁力驱动的阻尼驱动摆实验装置系统,通过数值模拟研究该系统参数共振和混沌的存在性及其相互关系.同时,对于磁力摆系统表现出来的有趣物理现象背后的动力学行为,学者们同样开展了一些研究.D’Alessio[20]通过数值模拟研究3 个永磁铁呈等边三角形排布的磁力摆装置的摆球运动轨迹路线,提出该系统对初始条件的敏感依赖性,是演示与“蝴蝶效应”[21]相关联和类比天气预测的一种简化系统.Mann[22]研究了由1 个横向放置的单摆和2 个磁铁组成的磁力摆实验装置系统的动力学行为,对准稳态逃逸准则进行了拓展,得出1 个平衡点的振荡能克服相邻的势垒并逃逸到相邻的吸引子的阈值准则.James 等[23]通过数值模拟研究了4 个永磁铁呈正方形排布的磁力摆装置系统,得出该系统摆球复杂运动轨迹与分形有关,并通过估计分形维数来研究摆球对初始条件的敏感性现象.从目前的研究进展来看,典型磁力摆系统存在初值敏感性行为是公认的事实,但是引起该现象机制的理解尚存在分歧:有些学者认为该现象应归因于混沌或瞬态混沌,另外一些学者认为该现象源于吸引域分形.

为此,本文考虑一类磁铁位置可调节的典型磁力摆系统,分析其全局动力学行为,特别是初值敏感性现象的机制.首先,对该类磁力摆系统建模;然后,变换磁铁位置,分析不同磁铁分布情况下磁力摆系统的平衡点个数和稳定性;最后,数值模拟磁力摆系统的初值敏感性现象,并设计实验验证该现象.

2 磁力摆动力学简化模型

本文以一类等边三角形排布的磁力摆为研究对象,磁力摆实物图如图1(a)所示,磁力摆改进模型示意图见图1(b),其中横竖支杆作为吊接摆球装置,小圆盘作为放置3 个永磁铁装置,大圆盘设置有滑槽,配合小圆盘移动永磁铁位置,U 形支座用于校验实验装置是否水平,磁力摆简化计算模型如图1(c)所示.在建立磁力摆运动数学模型方程之前,作出以下三点理想化假设[24]:

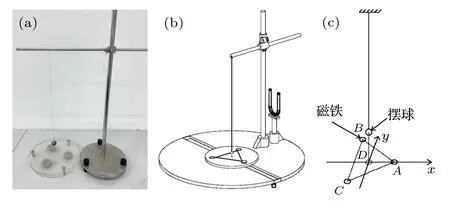
图1 磁力摆 (a) 实物;(b) 改进模型;(c) 简化计算模型Fig.1.Magnetic pendulum:(a) Real object;(b) improved model;(c) simplified calculation model.

1)磁力摆吊线的长度远远要比磁铁间的距离长,因此,可以假定摆球是在平面上而不是在较大半径的球面上运动,即保持D不变.

2)磁铁是1 个吸引点,位于磁铁放置基底平面上,3 个磁铁在平面上呈等边三角形放置,即AB=AC=BC,且每个磁铁中心位于等边三角形顶点上.

3)某个磁铁作用在摆球上的力与两者的距离的平方成反比.

现在考虑单个磁铁与摆球受力情况.在摆球位于平衡位置时,单个磁铁投影到摆球平面位置如图2 所示,摆球质心在xy平面运动,磁铁位于xy平面下面,与平面距离为D.因而,假定摆球质心位于(x,y,0) ,某个磁铁位于(xj,yj,−D),由图2可得距离m和n,于是角度α的余弦为

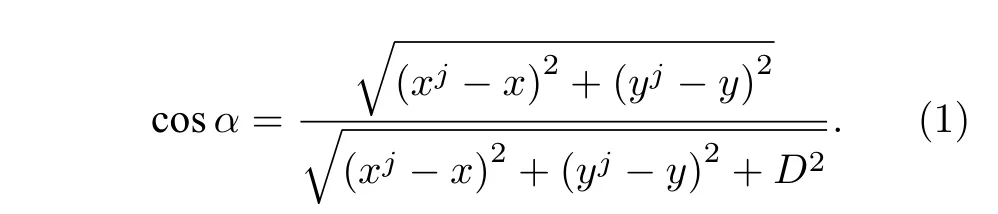
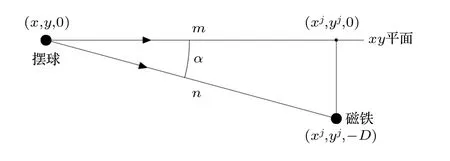
图2 摆球与单个磁铁位置示意图Fig.2.Position diagram of pendulum ball and single magnet.

根据库仑第二定律,磁铁施加在摆球上的力与这两点间的距离平方(xj −x)2+(yj −y)2+D2成反比[24].然而,根据理想化假设1),摆球质心运动可看作位于xy平面,因此,利用余弦的基本表达并经过某些变换后,投影得到x方向上的力正比于同理,可得到y方向上的力.同时,考虑将摆球拉回到xy平面中心的重力和线性黏性阻尼力,其中,无量纲化线性黏性阻尼系数为0.2[24].利用牛顿第二定律,对位于初始位置的3 个磁铁构成的磁力摆装置,来自磁铁的力是3 项矢量和,同时考虑3 个磁铁位置可移动,以移动3 个磁铁中心位置的xj值为例,保持每组磁铁位置yj不变,坐标系原点在3 个磁铁组成的等边三角形形心位置,将各力投影到x,y方向,将所有项移到等式左边后,得到该磁力摆无量纲化运动微分方程为[20]

3 平衡点个数与稳定性分析

为了研究不同磁铁分布情况下该磁力摆平衡点的个数和稳定性,首先利用(3)式得到7 组移动距离和移动的磁铁位置,每组磁铁的中心投影到xy平面上的位置如表1 所列.

表1 磁铁移动位置Table 1. Magnet moving position.

为了得到每组每个磁铁在不同位置时的平衡点,对(2)式进行变换得

对比表1 和表2 可以得出,每组的前3 个平衡点位置与每组磁铁中心投影到xy平面上的位置非常接近,但并不重合,剩余的平衡点位置离磁铁中心投影到xy平面上位置较远.

为了研究每组平衡点处的稳定性问题,首先对(2)式进行状态方程变换得

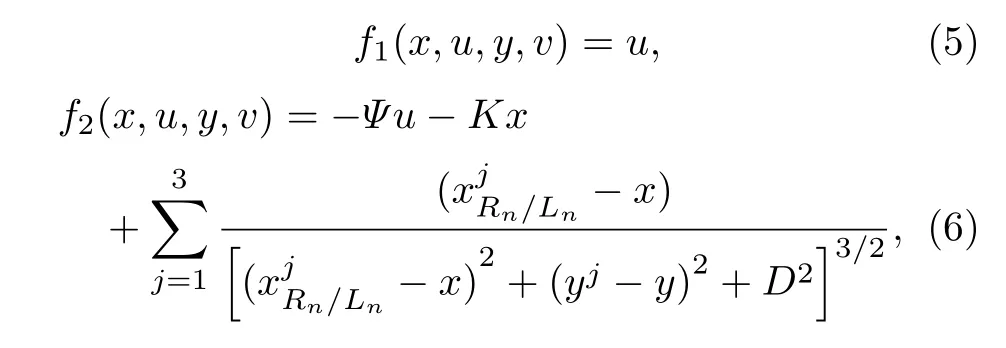
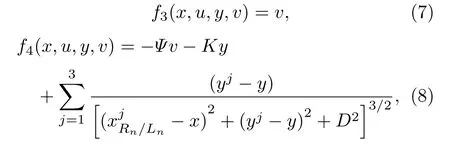
从而将7 组不同磁铁位置的平衡点稳定性转化成为讨论(0,0) 点稳定性;进而,作位置平移变换:

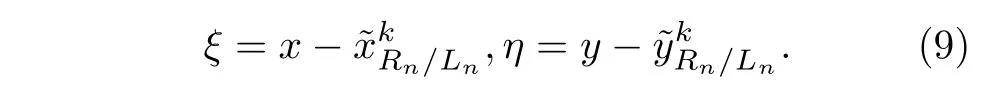
为此,将(5)—(8)式在零平衡点处进行泰勒展开,得到该磁力摆系统的雅可比矩阵,代入3 个磁铁7 组不同的位置值、平衡点值和Ψ=0.2 ,K=0.5 ,D=0.25 参数值,分别计算得到每组平衡点处的特征值,因为每组均有平衡点位置关于y轴对称,故对称的平衡点处的特征值相同.

根据计算,表2 中每组除前3 个平衡点位置,其他平衡点处的特征值实部均存在大于零的情况,故均不稳定.而表2 中各组前3 个平衡点均具有零实部特征值,具体对应的特征值情况如表3 所列,因此,适用李雅普诺夫第一法[25]稳定性判定定理来判断这些平衡点的稳定性,具体稳定性判定如下.

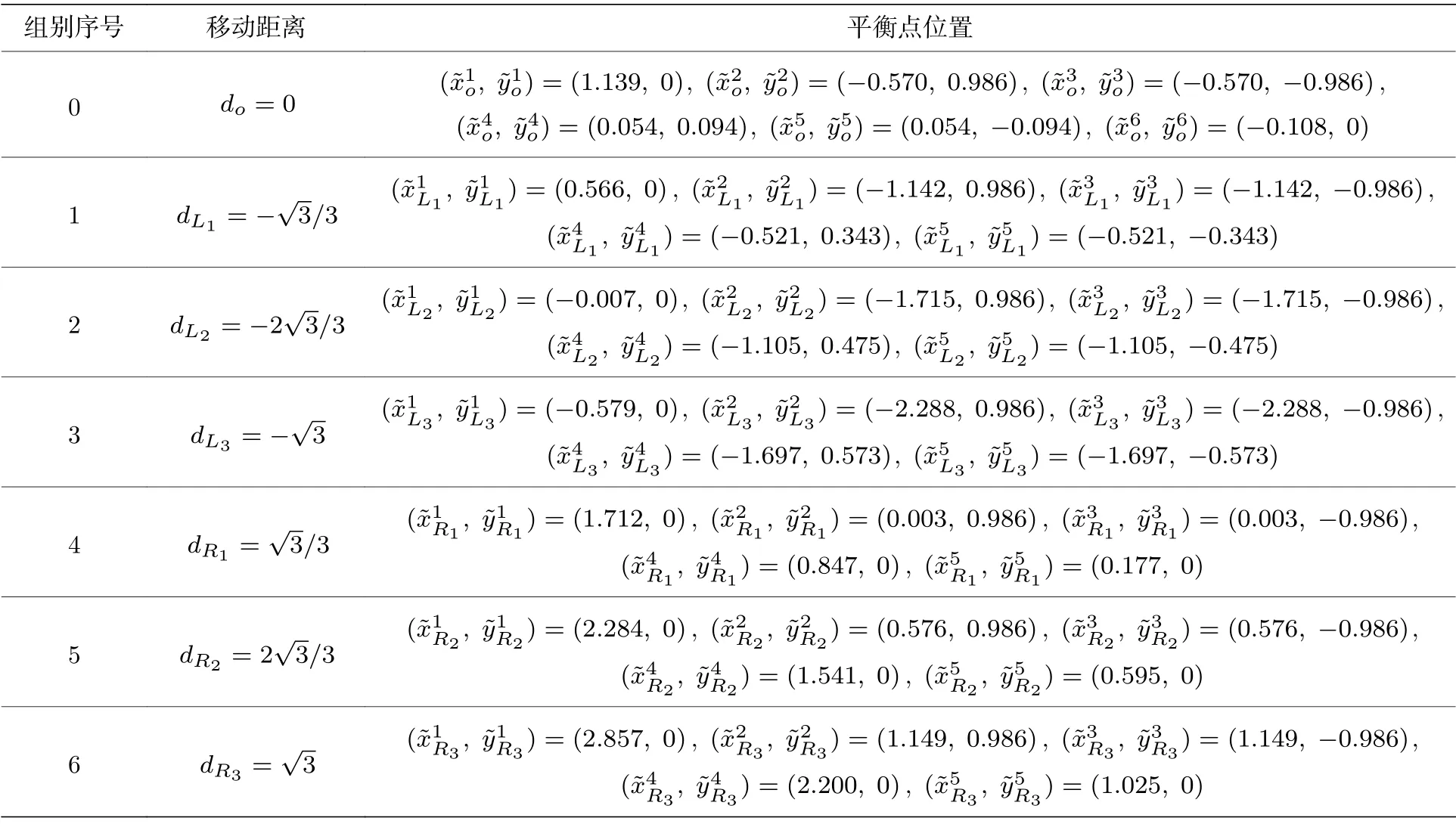
表2 7 组不同磁铁位置的平衡点Table 2. Seven groups of equilibrium points with different magnet positions.

根据(5)—(8)式可以得到系统雅可比矩阵,忽略关于x和y的二阶及以上项次,进一步化简得到原系统近似雅可比矩阵为(10)式,其中yj,D)为(11)式,对应各组平衡点雅可比矩阵为

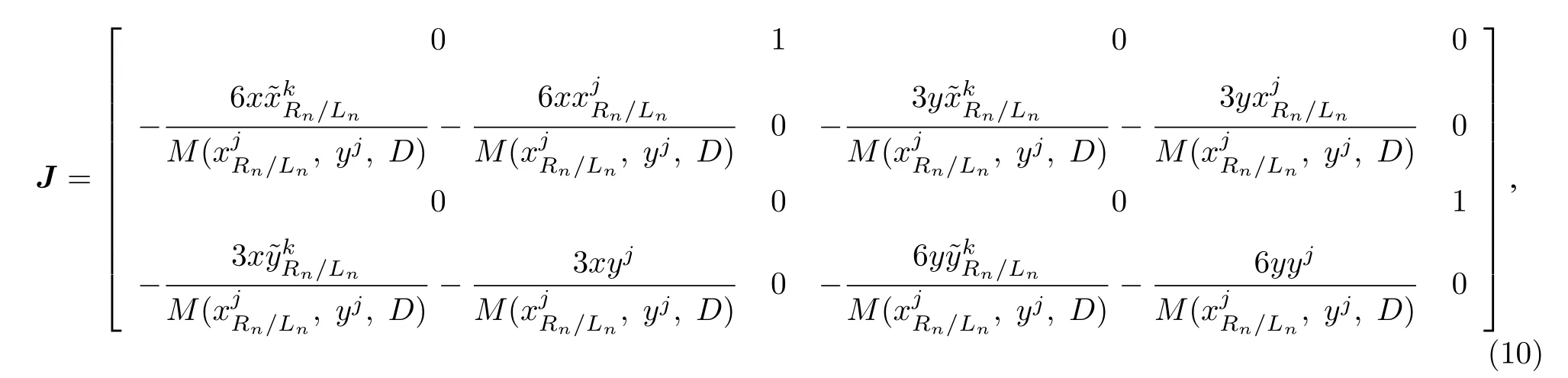
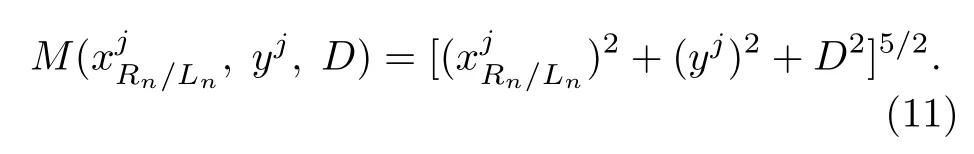
根据李雅普诺夫第一法[25]判断每组平衡点处稳定性,如果平衡点处特征值的实部等于零重数,且与其特征子空间维数相等时,该平衡点稳定,否则不稳定.以表3 中序号组别第0 组为例,计算求解平衡点特征值所对应特征子空间维数,其他组求解同理可得.代入第1 个平衡点位置和参数D值可得其特征值为.根据特征子空间的定义,即特征值的特征向量再添上零向量的集合为属于特征值的特征子空间[26].此时,计算得到其所对应的特征子空间为

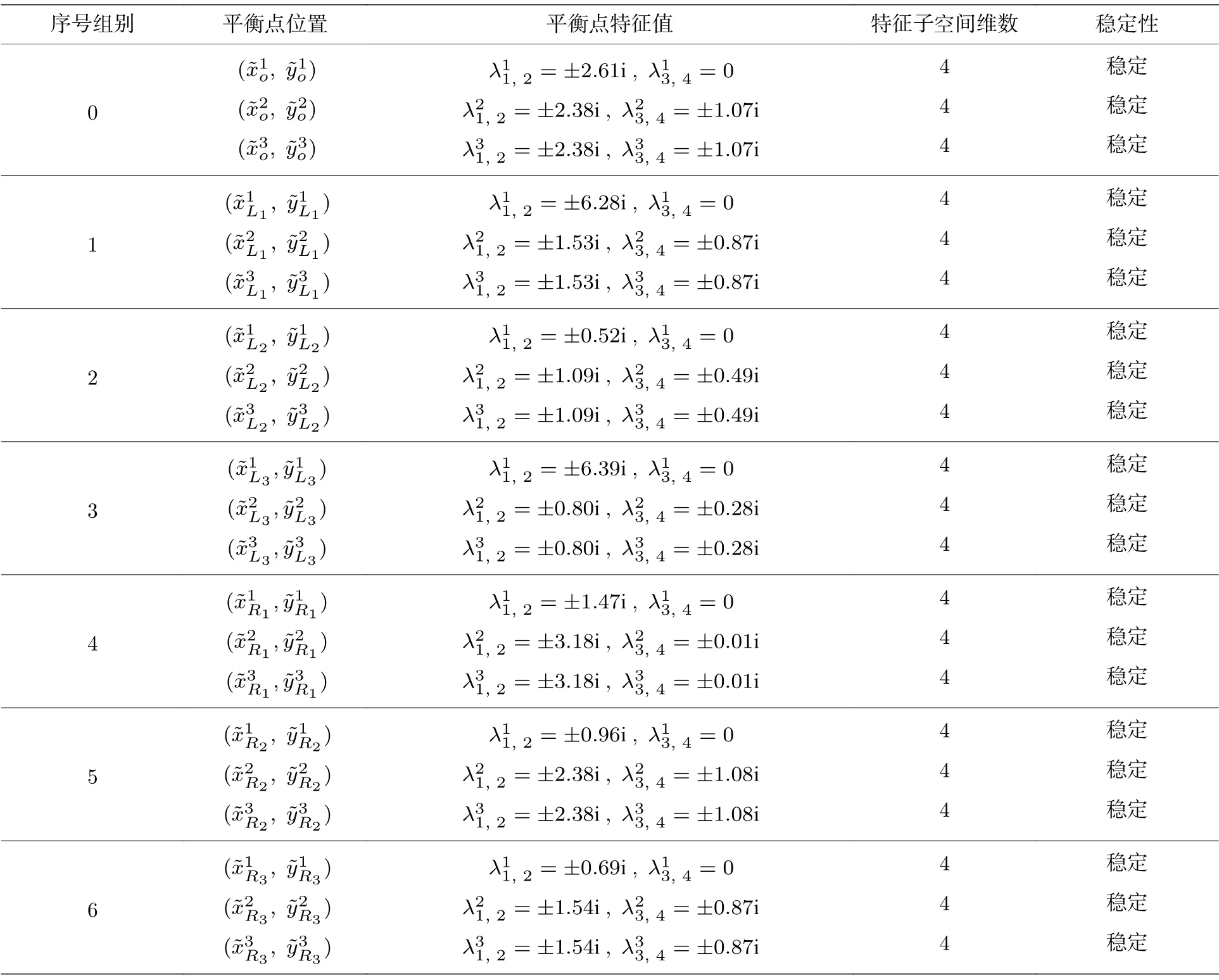
表3 磁力摆系统移动磁铁位置时稳定的平衡点判定结果Table 3. Results of judging the stable equilibrium point when the magnetic pendulum moves the position of the magnet.

因此,特征子空间N1维数为4.类似地,第2 个平衡点所对应的特征值是两对纯虚根,进而,计算得到其所对应的特征子空间为

特征子空间N2维数同样为4.由于表3 中每组第3 个平衡点位置与第2 个平衡点位置关于y轴对称,故特征值相同,所对应的特征子空间维数也相同,即也为4.同理可推导表3 中其他序号组别中平衡点特征值和所对应的特征子空间维数,具体结果见表3,所有平衡点特征值的实部等于零重数,为4,等于所对应的特征子空间维数.因此,满足李雅普诺夫第一法[25]判断平衡点处的稳定性定理,故为稳定的平衡点,即不动点吸引子.

根据表3 中平衡点稳定性判定结果可得,不论是磁铁位置未移动时还是磁铁位置移动后均存在3 个稳定的平衡点,即该系统存在3 个共存点吸引子现象,且投影到xy平面上位置接近磁铁中心.为探究磁铁位置移动时吸引域的分形演变规律,下节将利用数值模拟来研究7 组不同磁铁位置时的不动点处吸引域.

4 数值算例

本节在研究该磁力摆系统吸引域的分形问题时,(2)式是由二阶常微分方程构成的系统,需要指定摆球位置(x,y) 和速度(),摆球位置是在磁铁位置周围的正方形内变化的,因此,本文将初始速度设为(0)=(0)=0,且(2)式中参数设定为Ψ=0.2,K=0.5,D=0.25 不变.

当磁铁位置未移动(即当摆球可投影到3 个磁铁对应的等边三角形的形心位置)以及改变磁铁位置时,摆球从不同的位置释放,可以通过摆球运动轨迹路线不可预测性来阐明初值敏感性现象.当磁铁位置未移动时,设定3 组不同的摆球出发位置依次为(−0.5,−0.03),(−0.5,0.02) ,(−0.5,0.03),摆球运动轨迹及各初始条件对应的x和y时间历程数值模拟结果如图3(a)所示,其中,绿色轨迹线和对应的时间历程图为摆球从(−0.5,−0.03) 出发运动,可以看出摆球在绝大多数时间内在磁铁C吸引子中心投影到xy平面上的位置附近杂乱运动,最终静止在磁铁C中心投影到xy平面上的位置;蓝色轨迹线和对应的时间历程图为摆球从(−0.5,0.02)出发运动,可以看出摆球最终静止在磁铁A中心投影到xy平面上的位置;红色轨迹线和对应的时间历程图为摆球从(−0.5,0.03) 出发运动,可以看出摆球最终停止在磁铁B中心投影到xy平面上的位置.当磁铁位置改变,即对应表2中序号组别为4,移动距离时,设定3组不同的摆球出发位置,依次为(−0.6,−0.09) ,(−0.6,0.03),(−0.6,0.09),摆球运动轨迹及各初始条件对应的x和y时间历程数值模拟结果如图3(b)所示.同样,可观察到类似现象:绿色轨迹线和对应的时间历程图为摆球从(−0.6,−0.09) 出发运动,可以看出摆球在绝大多数时间内在磁铁C吸引子中心投影到xy平面上的位置附近杂乱运动,最终静止在磁铁C中心投影到xy平面上的位置;蓝色轨迹线和对应的时间历程图为摆球从(−0.6,0.03) 出发运动,可以看出摆球最终静止在磁铁A中心投影到xy平面上的位置;红色轨迹线和对应的时间历程图为摆球从(−0.6,0.09) 出发运动,可以看出摆球最终停止在磁铁B中心投影到xy平面上的位置.图3(a)和图3(b)中白色“+”号表示3 个磁铁中心投影到xy平面上的位置,对比图3(a)和图3(b)可以得出,其中绿色轨迹线都表示第1 组摆球出发位置的运动路径,蓝色轨迹线都表示第2 组摆球出发位置的运动路径,红色轨迹线都表示第3 组摆球出发位置的运动路径,3 组摆球起始出发位置的变化非常微小,每一组摆球运动轨迹都无法预测,反映了摆球动力学行为对初始条件的敏感依赖性.

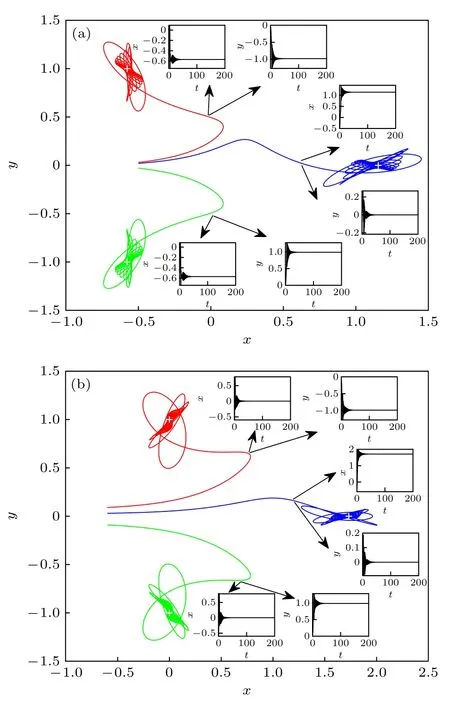
图3 摆球不同出发位置时运动轨迹和时间历程 (a) 磁铁位置未移动时;(b) 磁铁位置移动时Fig.3.Movement trajectory and time history diagram of the swing ball at different starting positions:(a) When the magnet position is not moved;(b) when the magnet position moves.

现研究7 组磁铁在不同位置时不动点吸引域分形演变规律,因为该磁力摆吊线的长度远远要比磁铁间的距离长,所以可以假定摆球是在xy平面上运动划分不动点吸引域.由表1 可得,设定磁铁未移动位置,此时摆球投影到3 个磁铁对应的等边三角形的形心位置,磁铁位置作为参照,数值模拟分形吸引域如图4 所示.在往x轴负方向移动的第1 组中3 个磁铁位置依次为其中j=1,2,3,数值模拟分形吸引域分别如图5(a)—(c)所示.从磁铁未移动的位置处开始往x轴正方向移动的第1 组中3 个磁铁位置依次为其中j=1,2,3,数值模拟分形吸引域分别如图6(a)—(c)所示.

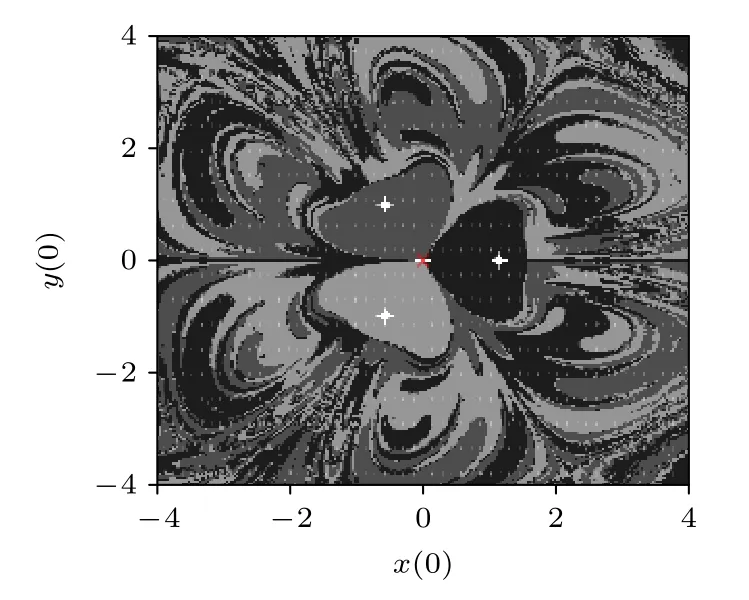
图4 磁铁位置未移动时分形吸引域Fig.4.Diagram of fractal domain of attraction when magnet position is not moved.

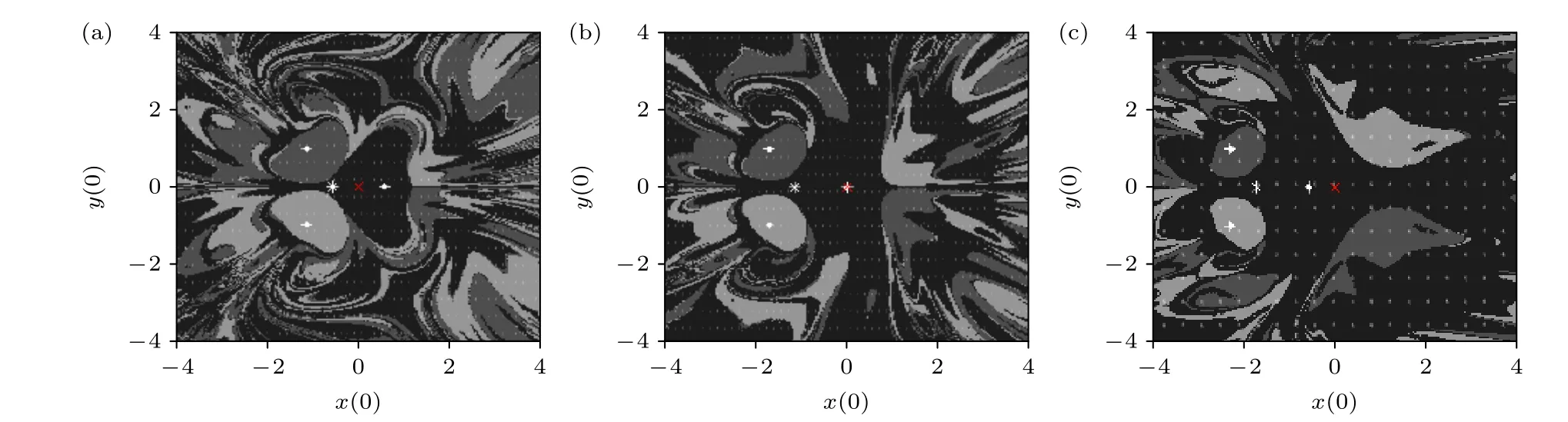
图5 向左方向平移时分形吸引域随磁铁位置演变Fig.5.Evolution of fractal basin of attraction of the attractors under different translation distances of magnet position to the left:

在图4—6 中,白色“+”号表示每组3 个磁铁的中心投影到xy平面上的位置,白色“•”号表示稳定的平衡点即不动点位置,白色“∗”号表示3 个磁铁对应的等边三角形的形心投影到xy平面上的位置,红色“×”号表示摆球平衡位置投影(0,0) 处.其中,黑色区域为最靠近磁铁A的吸引子的吸引域,深灰色和浅灰色区域分别对应靠近磁铁B和C的吸引子的吸引域.由图4 可见,当摆球可投影到3 个磁铁对应的等边三角形的形心位置时,3 个磁铁吸引子A,B,C的吸引域尺寸面积相当,呈中心对称状,边界分形明显,因此体现初值敏感性现象.对比图4 和图5 可得出:各不动点位置与磁铁中心投影到xy平面上的位置并不重合,而存在微小的偏差;从摆球可投影到3 个磁铁对应的等边三角形的形心位置出发,随着3 个磁铁位置往x轴负方向移动,离摆球平衡位置投影点(0,0) 处最近的1 个磁铁A吸引子的吸引域明显变大,成为强势吸引域,而另外吸引子的吸引域则被迅速侵蚀;类似地,不难发现,当3 个磁铁从摆球可投影到对应的等边三角形的形心位置往x轴正方向移动时,对比图4和图6 可以得出,离摆球平衡位置投影点(0,0) 处最近的2 个磁铁B,C吸引子的吸引域同样变得越来越大,而离摆球平衡位置投影点(0,0) 处最远的1 个吸引子吸引域尽管迅速消减,却始终存在.由此可见,移动磁铁位置会引起各吸引子吸引域的变化,却不会对其吸引域分形形态产生本质影响.

图6 向右方向平移时分形吸引域随磁铁位置演变Fig.6.Evolution of fractal basin of attraction of the attractors under different translation distances of magnet position to the right:

5 实验验证

本节将通过实验来验证该磁力摆系统的初值敏感性现象.传统的实验验证方法[24]是在磁铁固定板上涂满荧光剂,然后在摆球上安装感光灯,使用荧光剂发光来跟踪摆球运动轨迹,但荧光剂发光亮度会受到限制,发光时间也有限,得到的实验轨迹图效果并不理想.为此,本实验采用可调节亮度的LED 微型信号灯(位置粘贴在摆球与吊线连接处,尺寸2 mm × 1 mm,质量2 mg),用摄像机延时拍摄功能直接跟踪摆球上的灯光轨迹,从而来直观记录下摆球运动的轨迹验证初值敏感性现象.由于LED 微型信号灯质量远远小于摆球(仅相当于摆球质量的0.04 %),因此忽略其质量,并不定性影响该系统的动力学行为.根据实验目标,准备如下实验装置器材:横向支杆、竖向支杆、紧固支杆螺栓、竖向支杆底座、圆形透明有机玻璃座、3 个扁平圆柱体钕铁硼永磁铁、带孔摆球、吊线、2 根直径为0.1 mm 细导线、1 个 2 20 Ω 色环电阻、1 个调节范围为0— 5 50 Ω的电位器、1 个LED 微型信号灯、5 V 电压接线、5 V 电源、摄像机、三脚支架等.具体整体实验装置如图7(a)所示,电路连接部分如图7(b)所示.在实验时,为了让摄像机能够更好地进行捕光工作,将整个实验装置放置在较暗环境下.同时,为减小实验效果误差,将摆球吊线涂成黑色,从而避免反光影响摄像机捕捉摆球上光轨.

实验多次记录摆球上LED 微型信号灯的运动轨迹,来对比验证摆球运动轨迹对初值的敏感依赖性.本实验选择了保留3 次可以代表验证初值敏感性现象的实验图像,如图8 所示.具体实验步骤如下:

图8 摆球不同出发位置时光轨运动轨迹 (a) 第1 次释放摆球光轨运动轨迹;(b) 第2 次释放摆球光轨运动轨迹;(c) 第3 次释放摆球光轨运动轨迹Fig.8.Trajectory photo of light track in different starting positions of pendulum ball:(a) The trajectory photo of the first release pendulum;(b) the trajectory photo of the second release pendulum;(c) the trajectory photo of the third release pendulum.

1)如图7 搭建好实验平台,用记号笔记下摆球自然垂下时质心投影到水平工作台的位置,用黑色实心圆圈表示.然后将3 个永磁铁固定在圆形透明有机玻璃座上,3 个永磁铁等边三角形排布方向如图1(c)所示,磁铁B,C与y轴平行摆放,磁铁A处在x轴上.调整3 个永磁铁所组成的等边三角形,使形心投影到记号笔记下的黑色实心圆圈位置,并且调整摆球质心投影到3 个永磁铁等边三角形形心位置,保证摆球投影位置、3 个永磁铁等边三角形形心投影位置与记号笔记下的黑色实心圆圈位置重合.

图7 磁力摆实验装置 (a) 实验整体装置;(b) 电路连接Fig.7.An experimental apparatus for a magnetic pendulum:(a) Overall experimental device;(b) circuit connection.

2)接通5 V 电源,此时粘贴在摆球上的LED微型信号灯亮起,同时,将摄像机固定好位置,对准3 个永磁铁所处平面.

3)移动摆球偏离3 个永磁铁等边三角形形心距离为2 mm,并在起点位置标记红色“+”记号,开始第一次释放摆球,设置摄像机延时1 s 后开始记录光轨,给拨动摆球预留时间,按下摄像机开关,记录摆球上LED 微型信号灯的运动轨迹,直至摆球最终静止在某个永磁铁上方,此时,关闭摄像机开关,保存记录的图像如图8(a)所示.

4)保持摆球距3 个永磁铁等边三角形形心位置高度不变,移动摆球偏离3 个永磁铁等边三角形形心距离为3 mm,不同于第1 次释放摆球位置,并记录下此时起点位置,用红色“+”记号,然后,按下摄像机开关,记录摆球上LED 微型信号灯的运动轨迹,直至摆球最终静止在另一个永磁铁上方,此时,关闭摄像机开关,保存记录的图像如图8(b)所示.

5)重复步骤4)操作,需要注意的是释放的起点位置不同于第1 次、第2 次释放位置,移动摆球偏离3 个永磁铁等边三角形形心距离为4 mm,用红色“+”记号,最终保存记录的图像如图8(c)所示.

6)整理实验器材,清理实验平台.

在图8 中,摆球上的光轨会遍历3 个平衡点吸引子,轨线最密的地方代表其长期动力学行为.其中,红色“+”号表示摆球光轨起点位置,绿色“•”号表示摆球光轨最终停止位置.根据实验结果图8(a)可以看出,第1 次实验时移动摆球偏离3 个永磁铁等边三角形形心距离为2 mm,摆球光轨由起点开始绕3 个磁铁中心运动,最终停止在磁铁A吸引子中心投影到xy平面上的位置;从图8(b)的光轨可以看出,第2 次实验时移动摆球偏离3 个永磁铁等边三角形形心距离为3 mm,摆球光轨最终停止于磁铁B吸引子中心投影到xy平面上的位置;类似地,根据图8(c)的光轨可以看出,第3 次实验时移动摆球偏离3 个永磁铁等边三角形形心距离为4 mm,摆球光轨最终停止在磁铁C吸引子中心投影到xy平面上的位置.对比图8(a)—(c)可知,摆球出发的起始位置仅存在微小的不同,光轨运动轨迹却截然不同,并最终停止在不同的磁铁中心投影到xy平面上的位置,说明摆球的动力学行为具有明显的初值敏感性.这也验证了第3 节的理论预测和第4 节的数值仿真结论.

6 结 论

本文以对磁铁位置可调节的典型磁力摆为研究对象,建立了无量纲化动力学运动微分方程.改变磁铁位置,分析了7 组不同磁铁位置下磁力摆系统的平衡点个数,并判断了每组平衡点的稳定性.通过数值模拟研究磁力摆系统的初值敏感性现象及其机制和不同磁铁位置对应的吸引域演变规律.最后,通过实验验证该磁力摆系统的初值敏感性现象.主要得到以下结论:

1)该磁力摆系统存在3 个共存吸引子,初值敏感性现象归因于不动点吸引子的吸引域分形,而非混沌.

2)每组稳定的平衡点即不动点位置与磁铁中心投影到xy平面上的位置并不重合,而存在微小的偏差,偏差与重力恢复力相关的弹性系数和摆球距磁铁所在平面之间的最小距离这两个设计参数有关.

3)当摆球可投影到3 个磁铁对应的等边三角形的形心位置时,3 个磁铁吸引子的吸引域区域面积相当,呈中心对称状且分形,初值敏感性现象很明显.

4)移动磁铁位置会直接影响到3 个磁铁吸引子的吸引域形态,即离摆球平衡位置投影点近的磁铁对摆球影响最大,也就是离其最近的吸引子的吸引域会明显变得越来越大,其他吸引子的吸引域则会被侵蚀消减.