刚性对称陀螺分子Stark 效应的精确解*
2021-10-08陈昌远孙国华王晓华孙东升尤源陆法林董世海
陈昌远 孙国华 王晓华 孙东升 尤源 陆法林 董世海
1)(盐城师范学院物理与电子工程学院,盐城 224007)
2)(Catedrática CONACYT,CIC,Instituto Politécnico Nacional,CDMX 07700,Mexico)
3)(湖州师范学院量子物理研究中心,湖州 313000)
4)(Laboratorio de Información Cuántica,CIDETEC,Instituto Politécnico Nacional,UPALM,CDMX 07700,Mexico)
提出了一种精确求解位于外电场中刚性对称陀螺分子转动能级和相应解析波函数的新方法.首先利用不同形式的函数变换和变量代换将位于外电场中对称陀螺分子的极角θ 方向的方程转化为合流Heun 微分方程,然后根据合流Heun 微分方程和合流Heun 函数具有的特点,找到描述同一本征态的线性相关的两个解,构造Wronskian(朗斯基)行列式,得到精确的能谱方程.最后利用Maple 软件计算出不同量子态的本征值,再将得到的本征值代入本征函数进行归一化运算最终得到用合流Heun 函数表示的解析的归一化本征函数.这些结果可为深入研究对称陀螺分子的Stark 效应提供有益的帮助.
1 引 言
对称陀螺分子可分为两大类:一类为长对称陀螺分子,其3 个惯量主轴的转动惯量为IA

式中D是对称陀螺分子的电偶极矩,其方向在运动坐标系的z′轴方向;电场ε的方向在空间固定坐标系的z轴方向.由于附加项的出现,该方程至今都没有完整的精确解.当附加项系数Dε很小时,人们常用微扰理论来研究对称陀螺分子的Stark 能级.文献[1,2]给出能级准确到2级近似的结果,文献[3−10]给出能级更高级修正的结果,其中文献[3,6,7]还列出了用100 × 100 以及200 ×200 矩阵对角化方法得到的计算精度很高的精确值.以前的工作人们只专注于如何得到较为准确的能量本征值,而忽略了对本征函数的研究,这无疑影响了人们对刚性对称陀螺分子的Stark 效应的全面了解.
那么有什么方法既可获得准确的本征能量,又能得到解析的归一化波函数呢?根据我们最近对一维Mathieu 势的Schrödinger 方程[11]和刚性转子Stark 效应精确解的研究[12],以及对s=0 时角向Teukolsky 方程[13,14]精确解的研究,本文提出一种能精确求解对称陀螺分子Stark 效应的新方法.首先进行分离变量和变量代换x=cosθ(0 ≤θ≤π,1 ≥x≥−1),再利用不同形式的函数变换和变量代换方法把关于x的微分方程转化为合流Heun 微分方程,然后根据该方程及其解析解,即合流Heun 函数的特性,给出对应于同一本征态线性相关的两个解,并以此构造朗斯基行列式,给出精确的能量值必须满足的方程.借助于Maple软件中的合流Heun 函数及其一阶导数进行编程运算就能计算出精确的能量本征值,然后进行归一化运算给出的就是用合流Heun 函数表示的归一化的解析的本征函数.由于本文提出的方案不仅能得到精确的本征值,而且还给出用合流Heun 函数表示的解析的归一化本征函数.所以其结果将对研究对称陀螺分子的Stark 效应的能级分裂和振子强度等一系列实际问题带来极大的方便.
2 朗斯基行列式
令ψ(θ,ϕ,χ)=eiMφeiKχΘ(θ),并作变量代换x=cosθ,则定态Schrödinger 方程Hψ=Eψ可以分离变量,得到关于x的微分方程为
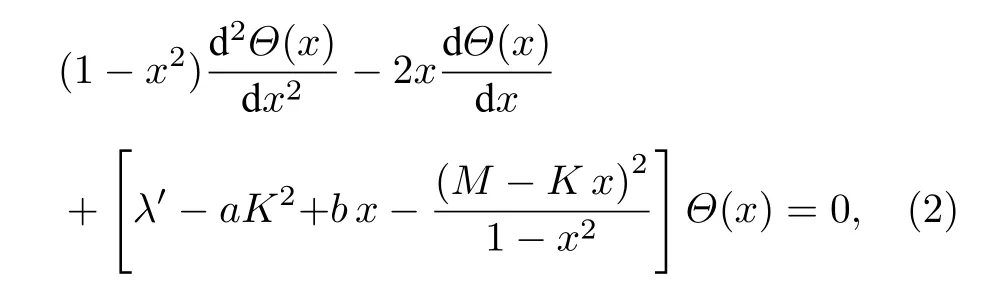
式中λ′=2IBE/ℏ2;b=2IBεD/ℏ2;M=0,±1,···,±J,K=0,±1,···,±J,其中J=0,1,2,···为对称陀螺分子的角动量量子数,M是角动量在空间固定坐标系z方向的投影量子数,K是角动量在空间运动坐标系z′方向的投影量子数.(2)式是典型的施图姆-刘维尔边值问题,当x→±1 时,本征函数Θ(x) 必须满足有限值这一自然边界条件.当没有外电场,即(2)式中b=0 时,微分方程(2)是可以精确求解的,其结果为[1,2]



式中2F1是n阶的超几何多项式.从(3)—(6)式可以看到,对于同样的状态(JKM),长对称陀螺分子和扁陀螺分子的能级是不一样的,但波函数的表达式相同.下面的研究表明,该特点在讨论对称陀螺分子的Stark 效应时保持不变.
为了统一研究长对称陀螺分子和扁对称陀螺分子,引入参数

当计算出精确的λ值后,不同类型的对称陀螺分子的能级为
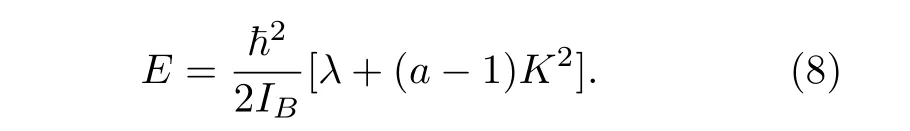
考虑到本征函数Θ(x) 在x→±1 时应满足有界的自然边界条件,首先对(2)式作如下形式的函数变换:
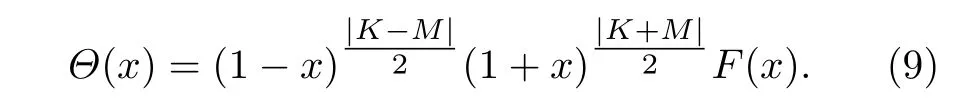
把(9)式代入(2)式得到F(x) 所满足的微分方程:

当合流Heun 函数 H eunC(α,β,γ,δ,η,z) 满足如下两个限制条件[15,16]:
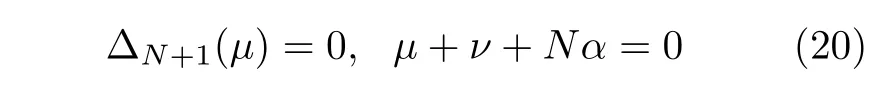
时中断为一个N次多项式,从而满足在z=1 处的自然边界条件.然而由(14)式可知,当b0 时,(20)式中的第2 个条件是不满足的.
正如上面分析的,由于限制条件(20)式中的第2 个是不成立的,所以只能保持(18)式为无穷级数的形式.当参数(K,M,b) 取确定值时,正确的λ值应该使得这个无穷级数解在(θ=π,x=−1,z=1)时也是有界的.因此找到正确的本征值λ是解决这一问题的关键.根据合流Heun 微分方程及其解析解合流Heun 函数的特性,如果对(10)式作变量代换,z′=1−z=(1+x)/2(−1 ≤x≤1,0 ≤z′≤1),那么(10)式将被修改为如下的合流Heun微分方程:
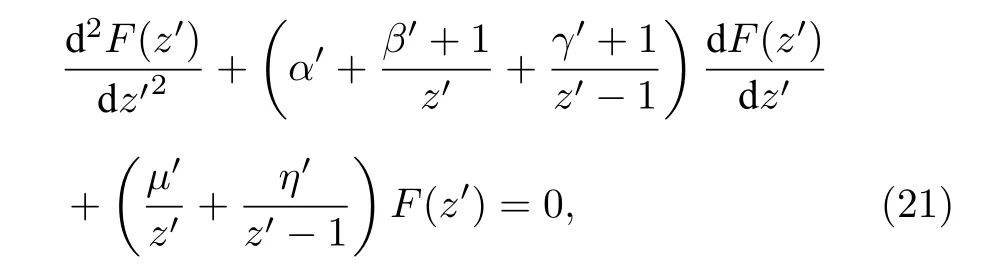
式中参数

由于β′=|K+M|≥0,所以(21)式的解也是合流Heun 函数

(23)式同样也不满足(20)式中的第2 个条件.这样由(9)式就得到在南极(θ=π,x=−1,z′=0)收敛的解为

注意到(18)式和(24)式都是微分方程(2)的解,因此对于同一本征态,它们只是数学表达形式不同而已.如果本征值λ是正确的值,那么这两个函数在南北极就应该都收敛,在开区间(−1,+1) 必须是线性相关的[17−19].这样对于两个不为0的任意常数C1和C2应该有C1Θ1(x)+C2Θ2(x)=0,将(18)式和(24)式代入约去共同因子就得到C1H(1)+C2H(2)=0 ,对其求一阶导数得C1H′(1)+C2H′(2)=0,由此就能得到如下的朗斯基行列式

注意到复合函数的求导规则并采用Maple 软件中的有关定义展开(26)式得

当参数(K,M,b) 取确定值时,由方程(27)可以求得精确的λ值.由于两个本征函数在整个开区间(−1,+1)都是线性相关的,所以为了方便起见取x=0.
3 本征值和归一化的本征函数
根据无量纲参数a=IB/IC,b=2IBεD/ℏ2的定义可知,它们的取值均为正实数.因此对应于(2)式的施图姆-刘维尔边值问题的算符
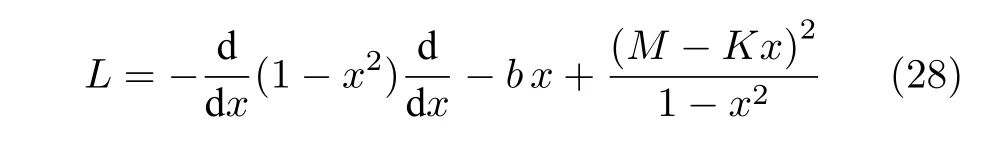
是一个厄米算符[17−19],所以本征值λ只能取实数值.由于不同本征值的本征函数必须是相互正交的,所以它们组成了函数空间的一个正交归一完备系.
首先讨论下列函数:

显然,它表示的是f(λ) 随本征值λ的变化情况,其与横轴交点的函数值是0,而对应的λ值就是相应的本征值.作为示例,图1 分别给出了几种情况下f(λ) 随λ的变化曲线.其中图1(a)是b=1,K=0,M=0,1,2,3,4的情况;图1(b)是b=5 ,K=1,M=0,1,2,3,4的情况;图1(c)是b=10 ,K=2,M=0,−1,−2,−3的结果;图1(d)是b=20,K=3 ,M=0,−1,−2,−3的结果.按惯例,约定J=n+|K+M|/2+|K −M|/2,则图中每一条曲线和横轴的第1 个交点对应于n=0,J=|K+M|/2+|K −M|/2,就是相应λ的最小值,下一个交 点n=1,J=1+|K+M|/2+|K −M|/2,就是相应的高1 个本征态的λ值,依次类推,这样从图形上就能知道每一个λ值的大小范围,而n正是对应本征函数的节点数.

图1 对称陀螺分子的 f(λ) 随λ的变化曲线 (a) b =1,K=0,M=0, 1, 2, 3, 4 ;(b) b =5,K=1,M=0, 1, 2, 3, 4 ;(c)b=10,K=2,M=0,-1,-2,-3 ;(d)b=20,K=3,M=0,-1,-2,-3Fig.1.Plot of f(λ) as the function of λ for the symmetric-top molecules:(a) b =1,K=0,M=0, 1, 2, 3, 4 ;(b)b=5,K=1,M=0, 1, 2, 3, 4 ;(c) b =10,K=2,M=0,-1,-2,-3 ;(d) b =20,K=3,M=0,-1,-2,-3 .
利用Maple 软件(版本号:ID1455132)编写程序计算(27)式,就能在给定精度下算出b取确定值对应不同的量子数(JKM)时λ的精确值,结果如表1 所列.把表1的λ值代入(8)式就可以给出精确的长对称陀螺分子a>1 或扁对称陀螺分子a<1的Stark 能级.根据量子数的取值范围以及(8)式、(27)式和表1 可知,刚性对称陀螺分子的Stark 能级具有如下特点:1)当|K|≥1 时,无外场时原来简并度为 2(2J+1)的能级分裂为简并度均为2的(2J+1) 条子能级,(K,M)和(–K,–M)能量相同;2)当K=0 时,无外场时原来简并度为(2J+1)的能级分裂为(J+1) 条子能级,±M的能级是简并的;3)由于外电场的影响,同一J值的各能级除了K=M=0 为单一能级外,其他的都是2 度简并的,简并能级的θ方向波函数是相同的,差别在于φ和χ方向的波函数是不一样的;4)当K=0时,长对称陀螺分子和扁对称陀螺分子不仅零级近似能量是相同的,而且Stark 能级分裂也是相同的,它们均退化为刚性转子的Stark 能级[12].需要指出的是,如果将本文得到的λ值的小数点后面的位数保留到与文献[3]相同的话,结果与用100 × 100 矩阵对角化方法得到的结果是一致的.为了比较本文的计算结果与微扰理论以及200 ×200 矩阵对角化方法的差别,以态(J,K,M)=(4,0,0)为例在表2 列出相应的结果.根据文献[1,2],准确到2 级近似,(4,0,0)态的近似结果为λ ≈(20+b2/154).由表2 可以看出,当表示外场强度参数b较小时(例如小于20),三者的计算结果基本上是相同的,但是随着参数b的增大,微扰理论显然就不适用了.不过本文的计算结果仍然与200 ×200 矩阵方法得到的精确结果相同(保留相同的有效位数),这解释了在文献中人们把用矩阵对角化方法得到的结果称之为精确值的原因.但本文提出的方法还能同时给出解析的归一化本征函数,所以本文的结果是令人满意的.不过需要说明的是,Maple 中有关函数的计算对某些特殊值特别是大参数时可能存在不足.期望随着Maple 版本的提高,这一现象会有所改善.

表1 对称陀螺分子λ的精确值Table 1. Precise values of λ for the symmetric-top molecules.

表1 (续) 对称陀螺分子λ的精确值Table 1 (continued). Precise values of λ for the symmetric-top molecules.
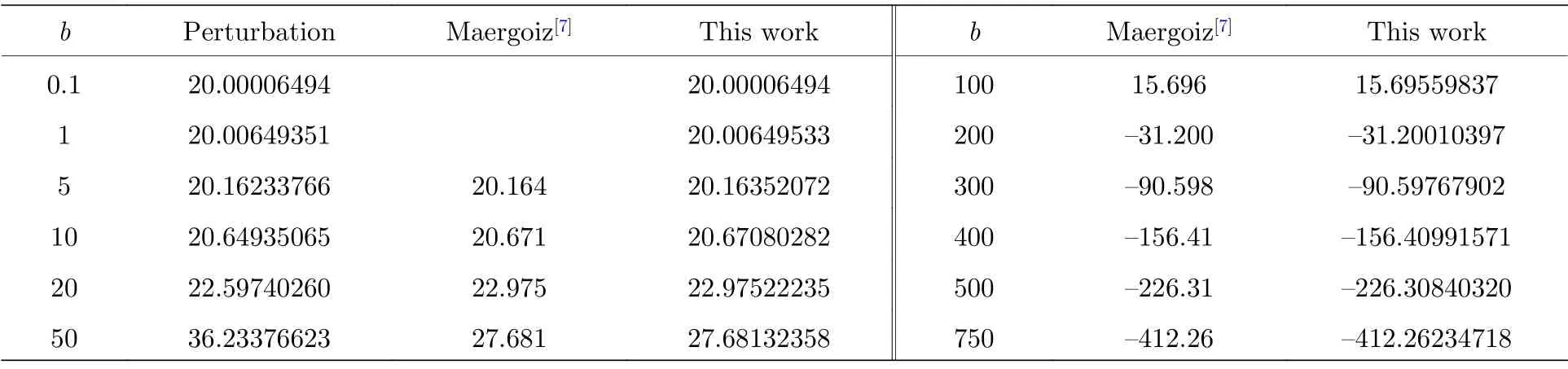
表2 对称陀螺分子(4,0,0)态的λ 值Table 2. Values of λ of the state(4,0,0) for the symmetric-top molecules.
下面讨论如何得到解析的归一化本征函数.为此将计算出的本征值代入(18)式和(24)式,得到的是未归一化的解析本征函数,经归一化运算后发现,这两个本征函数满足如下等式:

显然它们是线性相关的,如果用图形表示它们是完全重合的,(30)式中n=J −|K+M|/2−|K −M|/2=0,1,2,···是本征函数的节点数目.作为示例,图2分别给出了当b=1,J=1,K=1,M=1,n=0;b=1,J=1,K=1,M=– 1,n=0;b=10,J=3,K=1,M=1,n=2 和b=10,J=3,K=1,M=2,n=1 时N1Θ1(x) 和(−1)nN2Θ2(x)的函数图形.由图2 可见(30)式是正确的.
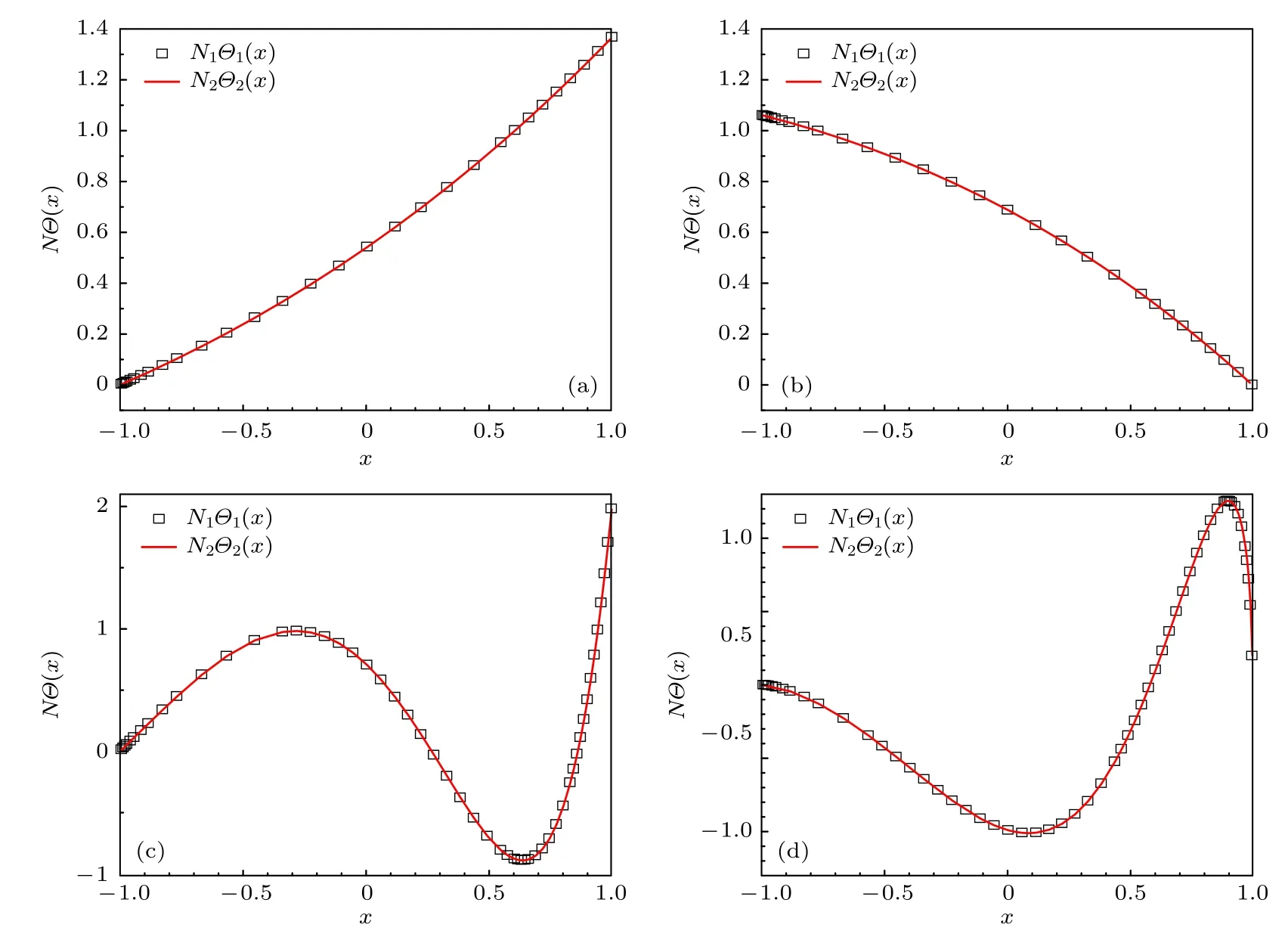
图2 N1Θ1(x) 和(-1)nN2Θ2(x) 是线性相关的 (a) b =1,J=1,K=1,M=1,n=0 ;(b)b=1,J=1,K=1,M=-1,n=0 ;(c) b =10,J=3,K=1,M=1,n=2 ;(d)b=1 0,J=3,K=1,M=2,n=1Fig.2.Linear dependence relation between N1Θ1(x) and(-1)nN2Θ2(x) :(a) b =1,J=1,K=1,M=1,n=0 ;(b)b=1,J=1,K=1,M=-1,n=0 ;(c) b =10,J=3,K=1,M=1,n=2 ;(d) b =1 0,J=3,K=1,M=2,n=1 .
最后根据(9)式和(30)式以及文献[1,2],给出位于外电场中的刚性对称陀螺分子完整的用合流Heun 函数表示的归一化的解析本征函数为

或者表示为

式 中x=cosθ,J=n+|K+M|/2+|K −M|/2是角量子数,M是角动量在空间固定坐标系z方向的投影量子数,K是角动量在空间运动坐标系z′方向的投影量子数,n是极角θ方向波函数的节点数,N1和N2是极角θ方向波函数的归一化常数,精确的λ值由数值计算(27)式给出.
4 结 论
综上所述,本文提出了一种能精确求解位于外电场中刚性对称陀螺分子定态Schrödinger 方程的新方案.首先利用不同形式的函数变换和变量代换方法把变量分离后得到的极角θ方向的微分方程转化为合流Heun 微分方程,然后根据该方程及其解析解合流Heun 函数的特性,给出对应于同一本征态线性相关的两个解析解,构造朗斯基行列式而得到能级所满足的方程.再利用Maple 软件编程计算就可以得到精确的能量本征值,结果与其他文献用100 × 100 或200 × 200 矩阵对角化方法得到的精确值在保留到小数后面相同位数情况下是完全相同的.最后进行归一化运算就给出了用合流Heun 函数表示的归一化本征函数.由此可见,本文提出的研究方法不仅能得到精确的本征值,而且还能获得归一化的解析波函数.显然,这一方法具有很强的实用性,其结果将对研究刚性对称陀螺分子Stark 效应的能级分裂和振子强度等一系列实际问题带来很大的方便.
