BP神经网络在地震噪声波形检测中的应用

巫立华，张宝剑，林彬华，戴丽金，张丽娜

（福建省地震局，福州350003）

0 引言

在地震观测台网中，观测仪器故障和台站周边环境异常干扰等因素，造成地震波形数据异常。如果这些异常数据应用于地震预警、烈度速报等应用系统中将产生严重的不良影响。为了自动检测地震波形数据质量，研究者们提出了通过计算地震噪声功率谱密度（power spectral density，PSD）检测地震波形数据的方法。地震环境噪声可视为平稳的随机信号，可以用PSD来描述地震台站记录到的噪声水平和特征[1]，1993年美国USGS的Peterson及其研究小组[2]通过分析全球地震台网75个台站近2000条地震噪声数据，确定了全球高噪声新模型（newhigh noise model，NHNM）和全球低噪声新模型（new lownoise model，NLNM）。在日常观测中，通过绘制地震噪声波形的PSD曲线与该模型曲线进行比较，从而判断地震波形数据的质量。该方法在国内外都得取得了良好的应用效果，2007年Sleeman等人[3]在Orfeus数据中心通过监测实时波形数据PSD值的变化，在VEBSN（Virtual European Broadband Seismograph Network）实现了对宽频带地震台网波形数据质量的自动检测；2008年廖诗荣等人[4]应用地震噪声功率谱概率密度函数（PDF，power spectrum probability density function）方法处理分析新建台站勘选数据的噪声水平；2012年林彬华等人[5]采用该方法开发一套监控系统，每天绘制测震台站的PSD图，并与该台站的历史噪声数据绘制的最低和最高噪声水平参考线进行对比，实现自动判断波形是否异常。

近年来，随着人工神经网络技术的不断成熟，越来越多的的研究学者将人工神经网络应用到地震领域，并取得了较好的应用效果。Pulli等人[6]以挪威NORESS台阵事件为资料，应用BP神经网络对天然地震各人工爆破事件进行识别；Thibaut Perol等人[7]应用卷积神经网络人工智能技术对美国俄克拉荷马州的诱发地震进行检测与定位，检测出比地震目录多17倍的地震；边银菊等人[8]采用BP神经网络对北京及周边的地震和爆破事件进行识别；徐程等[6]以滇西南地震数据为训练样本，采用BP神经网络进行地震震级预测；林彬华等人[9]采用BP神经网络技术对台湾海峡两岸震级偏差进行预测训练，并利用训练得到的BP神经网络自动校正了2018年台湾地震震级。

BP神经网络具有非线性映射能力强和网络结构简单等特点，应用广泛。本文采用BP神经网络方法对福建测震台网历史地震噪声波形数据进行学习训练，研究应用于识别PSD是否异常的神经网络模型，从而使地震波形检测更简单高效。

1 数据资料与处理方法

1.1 地震噪声波形数据收集

福建地震台网共88个测震台站，安装地震计包括短周期地震计10台，宽频带地震计30台，甚宽频地震计48台，具体型号见表1。

表1 福建测震台网地震计型号统计表Table 1 statistical table of seismometer modelsin Fujian Seismic Network

1.2 地震噪声功率概率谱密度计算方法

每条数据段中包含一个通道24 h原始波形数据，为了免去地震、爆破、标定等非地震噪声的处理环节，采用McNamara等人[10]提出的功率谱概率密度函数（PDF）方法进行地震噪声PSD值的计算。计算主要步骤如下：

（1）分割记录段。把24 h数据段以每12 min进行分割，一般来说，记录段长度的取值需达到需要获取信号的最长周期的6倍以上[11]，因此12 min长度，可以满足周期120 s低频地震噪声PSD值的需要。为了避免PSD值的变化过大，对每段记录间按50%的叠加率选取。

（2）PSD值计算。采用与Peterson相同的方法对每个记录段计算PSD值。

（3）平滑处理。为了使得到的PSD值在频率对数坐标中呈等间隔采样，采用1/3倍频程采样处理。

（4）PDF值统计。逐个频点统计PSD值落在对应频点的以1 dB为间隔的功率窗内的记录段数目，该数目与该频点总记录段数目的比值作为该频点该功率窗的PDF取值。

2 BP神经网络应用

2.1 BP神经网络原理

BP（back propagation）神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，由一个输入层、一个输出层和若干个隐含层组成，基本网络结构如图1所示。

图1 BP神经网络结构Fig.1 BPneural network structure

各层之间由神经元连接，每个神经元具有加权、求和和传递等基本功能。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阀值，使网络输出不断接近预期值，主要工作流程如图2所示。

图2 BP神经网络工作流程Fig.2 The working flow chart of BPneural network

2.2 训练集和测试集

从每段地震噪声波形处理后得到的PDF值中提取各频点概率密度值最大（MODE）的PSD值作为该段地震噪声波形各频点处PSD水平的估计值。把MODE曲线、NLNM曲线和NHNM曲线绘制在一张PSD图中，通过PSD图中MODE曲线的形态和噪声值判断该段地震噪声波形是否异常。MODE曲线形态与噪声模型基本一致且噪声功率值在噪声模型范围内则判断为正常波形的PSD图，其中短周期地震计由于频带限制，在低频端超出观测频带范围部分有明显偏高，若其它频带范围的曲线与噪声模型一致，也判断为正常。图3为正常波形的PSD图，其中图3（a）为宽频带地震计波形PSD，图3（b）为短周期地震计波形PSD。图4为主要典型异常的PSD图，图4（c）中MODE曲线低于最低噪声模型曲线，图4（a）、图4（b）、图4（d）、图4（e）、图4（e）MODE曲线的形态与噪声值都严重偏出噪声模型。

图3 正常波形的PSD图Fig.3 PSDof normal waveform

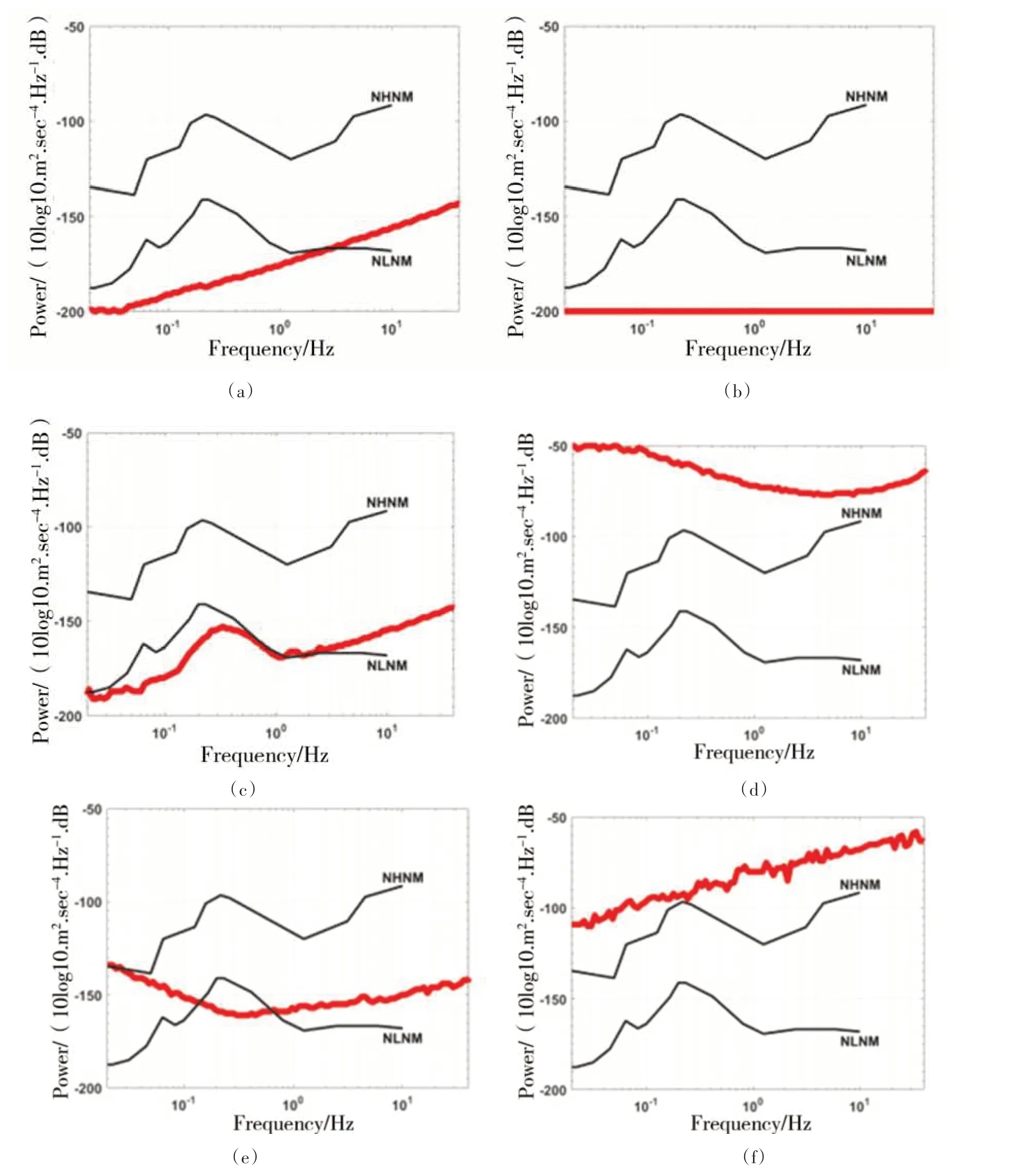
图4 异常波形的PSD图Fig.4 PSDof abnormal waveform

通过以上方法，在约12万个数据段的PSD值进中行逐一遴选，从中抽取了15 066条PSD图正常的PSD值，2988条PSD图异常的PSD值。把正常PSD值标记为0，异常标记为1。每类抽取约80%建立BP神经网络训练集，剩余作为测试集。

2.3 BP神经网络设计

2.3.1 BP神经网络结构BP神经网络的主要设计内容有网络层数、隐含层节点数、激活函数和训练函数。1989年Robert Hecht-Nielsen[11]证明了对于任何闭区间内的一个连续函数都可以用一个隐含层的BP网络来逼近，因而一个三层的BP网络可以完成任意的N维到M维的映射。基于此理论，本文采用一个隐含层的BP网络，激活函数采用log-sigmoid函数和purelin函数，训练函数选用traindx函数。

隐含层节点数对训练结果和训练效率产生决定性影响。根据研究，它主要取决于输入输出的非线性程度，即隐含层单元数与所要解决问题的复杂性、输入、输出单元的多少都有直接的关系。目前通常做法是采用经验公式得出一个估计值[12]。

式（1）中：M为输出单元数，N为输入神经元数，ɑ为1～10之间的常数。

本文中输入特征量为38，输出层单元数为1，ɑ取值10，根据估计值分别设计15、16、17三种隐含层节点数网络结构进行比对测试，根据测试结果选择最优的网络结构。

2.3.2 BP神经网络实现

采用MATLAB的神经网络工具箱塔建BP神经网络结构并训练和仿真[13]。主要流程如图5所示。

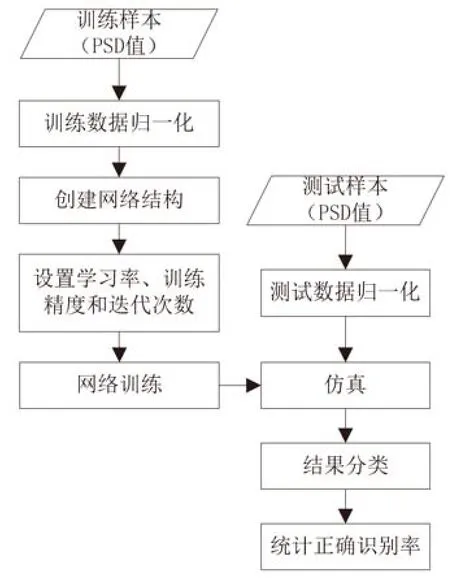
图5 BP神经网络设计流程Fig.5 Design flow chart of BPneural network

（1）归一化。BP神经网络中的激活函数S函数对[-1，1]区间的数值最为敏感，为了提高训练效率，输入样本数据一般情况都需要进行归一化处理。在MATLAB中可用premnmx（）函数进行归一化，把数据限定在区间[-1，1]。

（2）创建神经网络。采用NEWFF（）函数创建BP神经网络，通过该函数设定神经网络和各个网络层的节点数和激活函数，设置神经网络的训练函数。该函数创建的网络可自动初始化网络权值和阀值。

（3）网络训练。采用TRAIN（）函数进行训练，训练时通过设置学习率、训练精度和训练次数来达到训练目标。学习率控制神经网络训练过程中权值修正的步长，在BP神经网络设计中一般设置在0.01至0.001之间，训练过程中输出的标准方差如果快速线性下降，则所设置的学习率合理。训练精度根据训练样本数据目的数量级设置为0.001。训练次数初始为10 000，如果训练结果达不到训练精度则每次增加5000，直至达到训练精度。

（4）仿真测试。测试集数据进行同样的归一化处理后，用SIM（）函数进行仿真，验证训练后的神经网络结构检测效果。

（5）结果分类。在输入样本中正常标记为0，异常标记为1，因此仿真后预测结果小于0.5，则判定该样本对应地震噪声波形为正常，否则判定异常。测试集总共约3600个样本，判定结果与样本实际标记进行比较，统计判断正确的数目占所有测试数据的百分比。三种网络结构的测试结果见表2。

表2 不同隐含层节点数据测试结果Table 2 Test results of different hidden layer nodes

当隐含层节点数为16时，判定正确率为99.94%，该误差方差与节点数为15的方差接近，图6是该网络结构测试结果统计图，图中绿直线是判别分界线，只有2个异常波形的样本被误判为正常。根据测试结果最终选择检测地震噪声波形的BP神经网络模型网络层结构为38-16-1。

图6 隐含层节点数为16的测试结果Fig.6 Thetest resultsof hidden layer with 16 nodes

3 结论

通过计算地震噪声波形的加速度功率谱密度和绘制PSD图，进而判断地震噪声波形是否正常是一种成熟可靠且较为高效的波形质量监控手段。本文在此基础上，以PSD值为输入特征量，利用MATLAB设计并训练BP神经网络模型，并用测试样本对训练后的神经网络模型进行验证。结果表明，BP神经网络对异常PSD的识别率达99.9%以上，说明所设计的BP神经网络模型具有较高的预测能力，对地震噪声波形是否异常的检测具有一定的应用价值。

网络结构和训练参数的选择直接影响网络模型的训练效率和预测能力，但目前尚无完整统一的理论指导，只能根据经验进行对比测试选定相对较优的结构。因此如何选择更优的网络结构需要更多的实验和研究。此外，训练样本的数量和典型性对BP神经网络的泛化能力也有较大的影响，今后需进一步完善和优化训练样本数据，提高样本数量和典型性，从而提高网络模型的泛化能力。