工程结构中支撑减震结构响应及力学性能研究

史少华，石若利，刘 涛

（（1.四川文理学院建筑工程学院，四川 达州635000；2.云南大学建筑与规划学院，昆明650500）

0 引言

近年来，现有住房无法满足人民要求的矛盾愈加凸显，同时，随着炼钢技术的提升和改进，全国每年产钢率大大提高，这使得钢结构的得到不少关注，例如，Gholampour，Siroos等[1]通过对近场、远场平动构件和转动构件的分析，比较了有无转动构件对钢结构的影响。带支撑的钢框架结构因其独特的抗震耗能等优点受到极大关注，Skiadopoulos等[2]提出了一种新的基于力学的钢框架梁-柱-板区域节点抗震设计模型；Andres Gonzalez等[3]基于直接位移的设计方法对有偏心支撑框架建筑进行抗震设计，并通过非线性反应历史分析，对所建建筑物的性能进行了评估；Vahedi Niloufar等[4]用分析层次法优选具有专属抗震性能的混合钢框架；Yakhchalian，Masood等[5]评估了一些传统和先进的IMS（包括标量和矢量IMS）预测钢制屈曲约束支撑框架MRD承载力的有效性和充分性；郑宏[6]等对钢框架－桁架新型结构体系的抗震性能进行研究；王鹏[7]对高温差条件下的钢支撑的轴力变化进行分析；李晓瑾[8]对中心支撑在高层钢结构设计中的应用及分析进行研究。

随着理论和技术的进步，支撑方式对框架支撑结构抗震性的影响逐渐被许多学者注意到。欧阳号等[9]对不同布置方式的防屈曲支撑混凝土框架的抗震性能进行研究；邵永松等[10]研究了屈曲约束支撑布置方式对半刚接框架的抗震影响；王秀丽等[11]研究了屈曲约束支撑布置方式对钢框架的抗震性的影响。

上述是关于钢结构、支撑钢框架体系及支撑方式对结构性能的影响的研究，但是实际上支撑方式对结构抗震性能的影响的研究范围非常广。支撑方式大致可分为三类：中心支撑、偏心支撑和屈曲支撑。而合理的支撑方式及支撑的空间布置方式同样对结构受力具有重要作用，直接影响钢结构建筑的抗震性能和受力特点[12]。因此，本文借用PKPM软件分析支撑方式对结构抗震性能的影响具有一定的现实意义。同时，为框架支撑体系的支撑设计提供参考。

1 工程概况

本文所选取的建筑结构如图1，结构所占总面积为5992 m2，建筑高度为31.2 m，每层3.9 m，共8层，所选结构体系为应用最为广泛的钢框架体系，除了在结构四周设柱，沿结构纵向和横向每隔一段距离均有设柱。

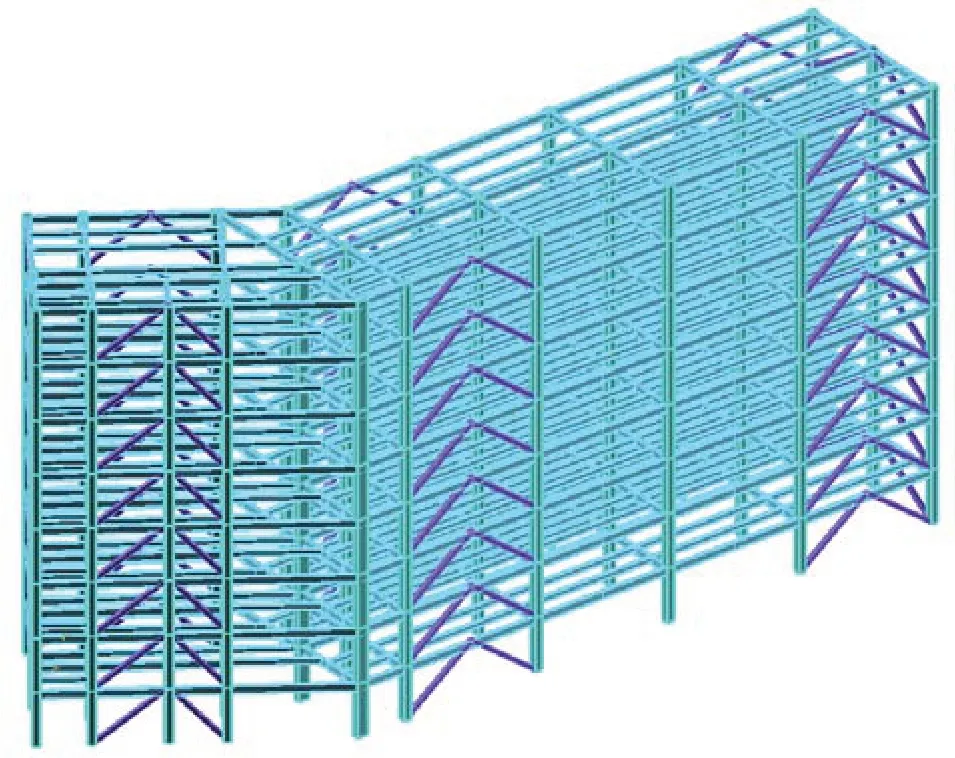
图1 八层钢结构轴测图Fig.1 Axonometric view of eight-story steel structure

结构原型位于安徽省某地区，基本风压定为0.55 kN/m2，基本雪压定为0.7 kN/m2，抗震设防烈度设置为8级，建筑结构安全等级是二级，设计基本地震加速度定为0.1 g，场地类别是Ⅱ类场地，设计地震分组是第一组。结构的标准层柱子轴线布置见图2。结构跨度适中，角柱采用矩形钢管混凝土GZ1，截面为箱型，截面尺寸为400×800×20×20mm，边柱采用矩形钢管混凝土GZ2，截面为箱型，截面尺寸为500×500×20×20 mm；梁均采用H型钢，其中，主梁截面尺寸为HM582×300 mm，次梁截面尺寸为HM440×300 mm；结构均选用型号Q235B的钢材。

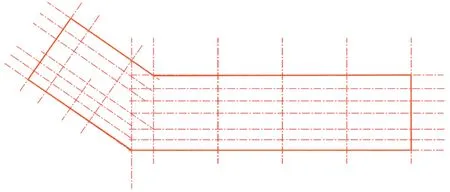
图2 柱子轴网布置图Fig.2 Layout of the column grid

2 支撑布置方案

本文通过改变纵向4跨结构的支撑方式，研究支撑方式对结构抗震性能的影响。方案一：在最左和最右的两跨框架上的每层布置一组交叉中心支撑；方案二：整个结构沿对角线方向布置一组交叉支撑；方案三：采用每两层两跨布置一组交叉中心支撑；方案四：最左跨和最右跨每两层布置单侧中心支撑，且沿中间柱对称，中间两跨每四层布置一组交叉中心支撑。四种方案的支撑布置方式均沿中间柱对称，均选用截面尺寸为300×300×20×20 mm的箱型支撑。图3为四种支撑布置方式，各方案的用钢量对比见图4。

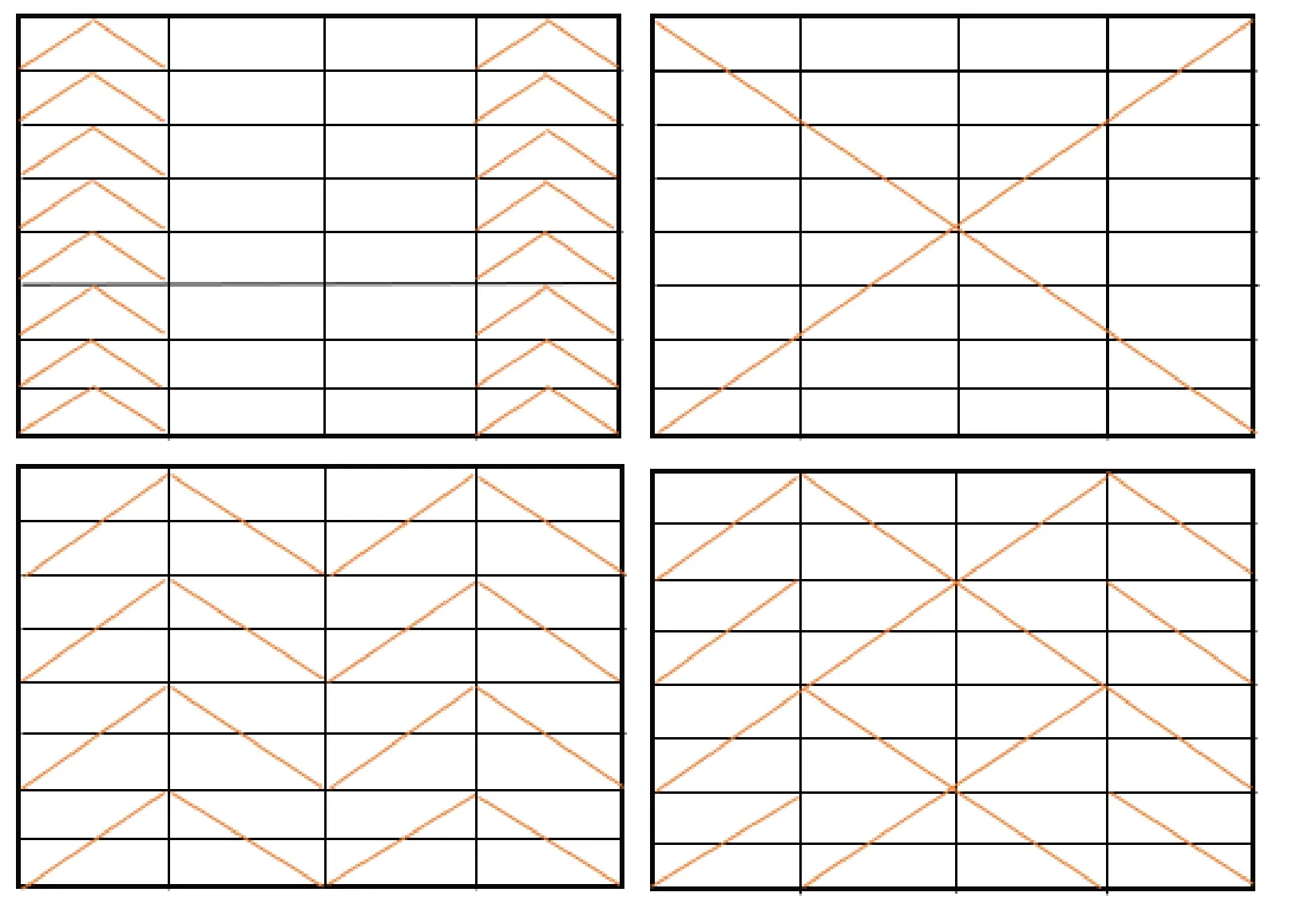
图3 四种支撑方案Fig.3 Four support schemes

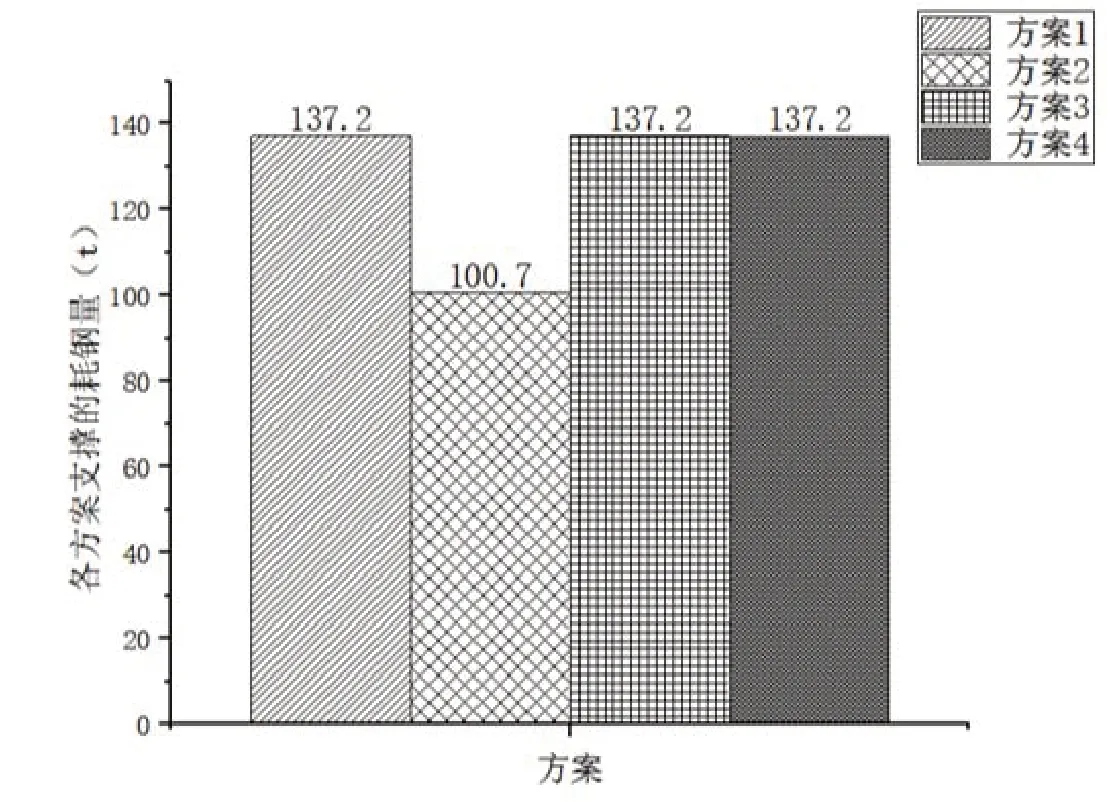
图4 各方案用钢量对比Fig.4 Comparison of steel consumption in each scheme

3 模型的有限元分析

3.1 模型的建立

本文利用PKPM对目标市场结构建模，PKPM是一款集建筑设什、结构设计、设备设计、节能设计为一体的综合类CAD系统[13]。四种支撑方案的空间模型如图5所示。其中，模型的材料和材料特性如下：钢梁、钢柱和支撑均采用钢材Q235，钢管混凝土柱采用C30+Q235的组合结构，其中钢材泊松比为0.3，弹性模量Es=2.06×105MPa，Ec=3.25×104MPa。

图5 四种支撑方案的空间模型Fig.5 The spatial model of the four support schemes

3.2 模态分析

根据相关规范[14]，在进行模态分析时，所选择的质量源应为恒荷载加上活荷载的0.5倍，其中质量源是指重力荷载代表值。4种方案不同支撑体系的前3阶振型周期见表1。

表1 结构模态分析结果Table 1 Structural modal analysis results

从表格中的数据可以看出，四种支承方案的前两阶与后两阶振型对应的分别是X平移、Y平移和扭转振动；X平移、扭转振动和Y平移。通过计算，扭转与平动的周期比分别为0.5829、0.6121、0.6139、0.6157，符合抗震设计规范中小于0.9的要求[15]。4种方案中，方案4周期比最大，其次是方案3及方案2，最小的是方案1，即方案1的扭转成分相对较小，由《建筑结构荷载规范》GB50009-2012的规定可对模型进行大致验算，具体验算方法见（1）式：

式中，T为该结构的自振周期，n为结构的楼层总层数。不难发现这四种方案在满足规范在自振周期方面的公式要求，也间接证明了模型的正确性。

通常，结构抗侧刚度与结构自振周期成反相关，根据表3.1数据得到方案2的X方向自振周期最大，其次是方案1，剩下的方案3、4相对较小，且十分相近，故采用方案2所示支撑布置方式时，结构抗侧刚度相对较弱，此时结构需要采取更多的加固措施以提高其抗侧刚度。方案3、4结构虽有相对较大抗侧刚度期抵抗变形的能力理应也相对强，但由于该方案的振型二均为扭转振动，其表现的地震响应不一定是最理想的，故还需进一步讨论方案1、2、3、4的地震作用下结构响应结果。

3.3 反应谱分析

为了研究在多遇地震强度下结构的响应，要对4种方案分别进行反应谱分析。阻尼比均取0.04，计算得到四种方案的结构各层平均位移，计算结果如表2所示。由表2可知，结构平均位移随楼层增加而增大，采用方案2布置方式时，结构侧向位移最小，其次是方案1，采用方案3、4布置方式时，结构位移最大，且相近。出现这种现象的原因可能是虽方案3、4的自振周期相对较小，抗侧刚度相对较强，但由于它们的扭转振动形态皆出现于第二振型，相较于方案1、2的前两阶振型均为平动，更不稳定，故受地震作用的影响更大，结构发生的位移也会相对较大。方案2与方案1的自振周期数值相近，且振动形态也相同，这时可能会由于不同支撑布置特点所存在的不同优势造成结构局部刚度等变化量不同，使得方案2所受地震作用下结构不利的响应弱于方案1.

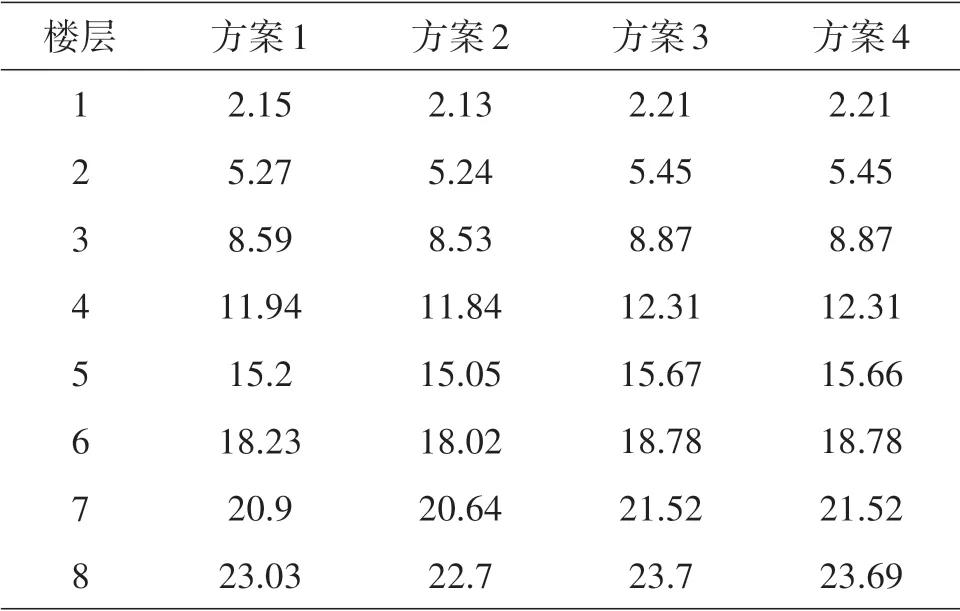
表2 各方案楼层平均位移（mm）Table 2 Theaveragedisplacement of floors in each plan（mm）

弹性层间位移角作为判断结构在小震情况下整体刚度的重要指标，由于此结构层数不高，因而主要控制因素不是风荷载而是地震作用，故应引起足够的重视。四种方案在地震作用下地板产生的最大弹性体位移角如表3所示。由表3可知，四种支撑方式均可以提高结构的整体刚度，同时，结构的变形还有较大的富余量。

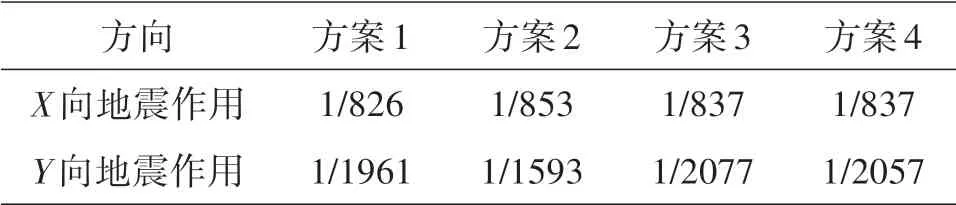
表3 各方案最大弹性层间位移角Table3 Maximum interlayer displacement angleof each scheme

3.4 Pushover分析

静力弹塑性分析方法是一种常见的方法，根据我国《建筑抗震设计规范》（GB 50011-2019）抗震规范，该方法可以运用于结构在罕遇地震下的计算。根据规范FEMA273定义的塑性铰，本文按照PKPM程序对其进行设置。梁体结构的塑性铰按照程序定义为M-M，只考虑弯矩屈服；柱体结构的塑性铰按照程序可以定义为P-M-M，要考虑弯矩和轴力的相关作用；而对于支撑结构只需考虑它的轴力。PKPM程序的荷载模式按照结构模态形式加载，定义X方向的荷载工况，设置当层间位移角达到1/50时分析终止。通过分析计算，PKPM程序找出了可以决定结构性能水平的性能点，即同一坐标系下需求谱和能力谱的交点。四种不同方案的最大基底剪力、塑性状态下结构的最大位移、最大层间位移角信息（即性能点信息），在罕遇地震作用下的数值如表4所示。

由表4可以看出，当用钢量相近时，方案1发生的位移较小，这是因为它的支撑杆件布置位置得当，结构的抗侧刚度较大，在地震作用下结构的塑性铰产生会延迟，相比而言，方案2、方案3、方案4三种不同支撑方案下，结构的抗侧刚度基本处于同一水平，发生的位移也基本相当。另外需要注意到，方案1的基底剪力显著大于其他三种方案，需要格外关注结构的基底应力变化，但经过验算，结构基底最大应力仍小于结构的承载力。

由表4的数据可知，现有方案最大层间位移角均小于1/50，故这些方案结构均满足抗震设防要求。

表4 各方案结构性能点信息Table 4 Information on the structural performance pointsof each scheme

3.5 主要构件的应力比和挠度

对结构不仅要进行整体分析，对各个构件的单独研究也非常重要。四种不同支撑设置方案中所加支撑、钢管混凝土柱的应力比如表5所示，由计算结果可以得出结论：改变纵向四跨中最左和最右跨的支撑布置，位于中间的跨梁柱应力比变化不大。

由表5中数据可见，四种方案下的支撑应力比均比较接近，这是因为它们使用的是截面相同的支撑，但是在方案1中梁与支撑有交点，导致该梁的应力比下降明显，相比其他方案小了10%左右。

表5 各方案主要构件应力比Table 5 Stress ratio of main components of each scheme

在每种方案中，钢梁与支撑有交点时，应力比为0.07～0.21，而纵向边跨与支撑无交点的梁应力比约0.63。要将应力比较小，即应力比为0.07～0.21的梁换为较大的应力比0.63。所以当分母中表示截面面积的数值减小时，应力比变大，每根梁能节省的用钢量大小由该值的减小量可以得到，再根据采用的钢材容重和梁的长度，计算出节约的用钢量，这都得益于支撑的合理布置。

不同支撑布置的耗钢量和四种方案所能节省的用钢量如表6所示。方案4、3、2、1所节省的钢材量逐渐减少。

表6 各支撑耗钢量与节省的钢材量Table 6 The amount of steel consumed and saved for each support

挠度是保证结构能否正常使用的关键。表7是四种不同支撑方案下此种梁产生的最大挠度，由于结构中跨的柱仅落在梁上，因而各方案中承受柱子荷载的梁挠度较大。由表7的数据可以看出：支撑的设置有助于减少梁段产生的挠度，因为有支撑的梁的挠度会比没有支撑的梁小很多。

表7 各方案中梁的最大挠度Table 7 Maximum deflection of beam in each scheme

4 结论

（1）方案1使每个跨层都有相同数量的支撑，虽整体节省钢材量最低，但结构的抗侧刚度提高显著，在小震和大震的作用下侧移均较小。但方案1的基底剪力显著大于其他三种方案，需要格外关注结构的基底应力变化，经过验算，结构基底最大应力仍小于结构的承载力。

（2）方案3、方案4由于结构特性相对方案1、2的稳定较弱，故其在小震和大震作用下侧移均较大，但该方案在节省钢材量上均高于前两者方案，虽其在地震作用下的相应较大，但离规范值皆有一定的距离，符合结构的延性设计要求，可最大限度地节约结构成本。

（3）方案2由于其在结构布置时采钢量皆少于另外三种方案，其在地震作用下的结构响应，如侧移量，梁最大挠度也相对较大，但与方案3、4结构下的响应差距不大，其布置特点也能在一定程度上节约相对较多的钢材，另外布置形式也较简单，最终的结构响应结果均在规范值内。在施工条件用钢量、作业环境等条件受限的情况下，可考虑采取此方案。

（4）综合考虑结构的抗侧刚度、延性、耗能能力和成本等因素，在施工条件均良好的情况下，方案1可作为最佳方案进行考虑，若在施工条件不是特别理想的情况下，方案2可作为减少经济成本及劳动力的优选。本文证实了支撑结构的许多优点，比如，支撑在框架结构起重要作用，支撑能增大结构刚度，提高结构抵抗变形能力，支撑的设置有助于减少梁段产生的挠度，提高结构安全性等。但同时，本文也有许多不足之处，比如，支撑分为中心支撑，偏心支撑和屈曲支撑，而本文仅讨论了中心支撑的布置方式对结构抗震性的影响。同时，现在的建筑结构因功能的要求，不规则、错层结构等也十分常见，因此关于一些特殊结构的建筑也可以进行相应研究。另外，本文还可以利用ABAQUS，ETAS建模，并进行结构分析，将所得结果与现有结果进行比较，这也是对现有结果的一种检验方式。