微波等离子体电子回旋共振放电粒子模拟分析

张 岩， 钱禹行， 刘尚合， 赵 鑫， 郭英军， 孙鹤旭

(1.陆军工程大学石家庄校区电磁环境效应国家级重点实验室， 石家庄 050003； 2. 河北科技大学电气工程学院， 石家庄 050018)

微波等离子体因其具有无极放电、放电区域集中、放电稳定等特点，在工业应用领域中尤其是功能材料的制备方面有着广泛的应用[1-5]。而电子回旋共振(electron cyclotron resonance, ECR)放电是微波放电的一种，相比传统的微波等离子体系统，采用电子回旋共振放电是更为先进的低温等离子体技术，它对微波源、微波反应腔的要求大为降低，提高了材料表面改性处理、微电子、大规模集成电路制造等领域中的低温等离子体加工水平[6-10]。

针对电子回旋共振放电问题，中外学者已经进行了相关研究，在理论、模拟方法上的研究已经非常成熟，例如，Sakharov[11]建立了二维全波模型，计算了X极化微波束在磁化等离子体中的传播和吸收，表明在真空磁轴上进行ECR加热是最佳的；Sánchez-Villar等[12]利用等离子体输运积分的混合粒子/流体模型和用于快速电磁场计算的频域全波有限元模型对电子回旋共振推进器原型进行了数值模拟，发现外加磁场决定了器件中功率的流动和吸收，并且功率吸收主要由电子回旋共振区的径向快速电场驱动；夏旭等[13]采用PIC/MCC(particle-in-cell with Monte Carlo collision)方法建立2 cm的电子回旋共振离子推力器仿真模型，研究了磁场结构对离子源内等离子体与壁面电流特性的影响；柯于俊等[14]采用有限元分方法进行流体仿真，研究了极靴对 ECR等离子体特性的影响。魏绪波等[15]利用有限元软件分析了微波、等离子体和电子束对微波窗的影响，并探究了微波窗损伤机理，延长微波窗使用寿命。上述研究为ECR应用技术的发展提供了依据，但近年来微波技术在ECR离子源中的作用，随着离子电荷状态和束流的增加而变得越来越重要，亟需对微波等离子体ECR放电特性展开深入研究。

为此，现使用PIC方法对微波等离子体电子回旋共振放电的电离过程进行了数值模拟，模拟了ECR放电过程中不同外加静磁场与不同微波频率下的电子能量分布以及微波电场强度与电子速度分布趋势。并与电子回旋运动的频率公式相印证，说明该模型能够正确反映ECR放电的物理过程。模拟结果反映了共振区域内，微波电场强度的大小会影响电子的加速效果及能量转换效率。旨在提出微波频率与ECR放电及其生成等离子体之间的作用规律，为ECR离子源中微波耦合加热等离子体的研究提供理论依据。

1 粒子模拟方法

粒子模拟方法[16-17]又叫粒子云网格，其主要思想是：首先将空间划分为若干个网格，并且将网格中的带电粒子所带的电荷通过加权的方式分配到网格点上，得到网格点的电荷密度分布，进而求解得到空间的电磁场分布，然后逐个跟踪带电粒子并求解每个带电粒子在空间电磁场作用下的运动规律，获得带电粒子的运动数据，最后对大量粒子的数据进行统计分析，得出等离子体的宏观性质。

PIC 方法是研究气体放电等离子体的有效手段之一，但是由于在实际放电过程中等离子体中带电粒子数目远远超出了当前的高性能计算机所能模拟计算的总粒子数。因此，根据实际情况建立了微波等离子体电子回旋共振放电的1D3V模型，其中，粒子在某一方向上同时存在位置的变化的和运动速度的变化，记为 1D；粒子的3个速度方向记为 3V。PIC模拟流程如图1所示。

t为时间；Δt为时间步长图1 PIC模拟流程图Fig.1 PIC simulation flow chart

采用PIC方法模拟微波等离子体电子回旋共振放电过程，而粒子模拟的主要研究对象是单个带电粒子，如电子、离子和中性粒子等，具体流程是：首先需要将空间划分为若干个网格，并假设大量带电粒子的初始位置和初始速度；然后将网格内的带电粒子所带的电荷分配到网格点上，得到空间网格点的电荷密度和电流密度分布；并求解出空间网格点的电磁场分布，其满足 Maxwell 方程组。

(1)

(2)

(3)

(4)

式中：D为电位移矢量；E为电场强度矢量；H为磁场强度矢量；J为电流密度矢量；B为空间的磁感应强度；ρ为空间电荷密度。

其次求解出带电粒子的受力情况，并根据Newton-Lorentz运动方程推算带电粒子在下一时刻的空间位置和运动速度，Newton-Lorentz运动方程的基本形式如下：

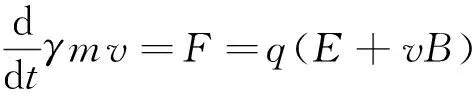
(5)

(6)

(7)

式中：q为带电粒子的电荷量；m为带电粒子的质量；F为带电粒子所受的力；x为带电粒子的位置；v为带电粒子的运动速度；γ为相对论因子。

在ECR放电系统中，因为波导系统采用的是TEM模式，所以只能得到x、y方向的有效微波电场强度，模拟中只考察x方向的有效微波电场强度Ex为

Ex=E0cos[2πω(n-1)Δt]

(8)

式(8)中：E0为微波电场强度幅值；n为运行时间步数；ω为微波频率。

模拟中带电粒子间不考虑碰撞，求得放电空间内平均电子能量(εave)分量，由于波导系统采用的是TEM模式，所以只需要求得平均电子能量在x和y方向的分量即可。

(9)

(10)

(11)

2 数值建模

微波等离子体ECR放电模型的示意图如图2所示，是具有轴向施加的静磁场的一维有界系统。圆极化的电磁平面波(微波)在左边界(z= 0)进入并沿z轴传播，到达右边界(z=L)。假定电磁波在x或y中没有变化。外部磁场Bext在z轴上保持恒定，ECR层位于整个放电系统。放电系统内带电粒子的位置仅沿z轴改变，但是带电粒子的速度被视为具有3个空间分量(1D3V)的矢量。

图2 微波等离子体电子回旋共振放电模型示意图Fig.2 Schematic diagram of microwave plasma electron cyclotron resonance discharge model

ECR放电属于微波放电，当图1中施加静磁场时，在洛伦兹力的作用下，电子作环绕磁力线的回旋运动[18-20]。

电子回旋频率公式为

(12)

式(12)中：e为电子电荷量；ωc为电子回旋频率。当通入微波的频率与电子回旋频率相等时，就会发生共振现象。

3 仿真结果与分析

根据图2建立的仿真模型，对微波等离子体电子回旋共振放电进行仿真分析。模型参数设置如下:空间间隔设置为3.3×10-5m，时间间隔设置为5.5×10-14s，微波波导采用的是TEM模式，微波磁感应强度的幅值设置为0.1 mT，微波电场强度的幅值设置为1.5×105V/m，平均电子温度设置为10 eV，平均电子密度设置为5×1017m-3。由于外加磁场是固定的，所以整个放电室内均满足与微波共振的条件，模拟中只考虑微波电磁场一个周期内的分布。

3.1 模型验证

由式(12)可知，对于 2.45 GHz微波，电子回旋共振形成条件通过计算得到需满足磁感应强度为 0.087 5 T。若计算结果符合电子回旋频率公式，即可验证该模型正确。图3给出了微波频率为2.45 GHz条件下，不同外加静磁场下x方向电子能量沿轴向分布，图4给出了x方向、y方向平均电子能量分布与x、y方向平均电子能量均方根分布。

图3 不同外加静磁场下x方向电子能量沿轴向分布Fig.3 Distribution of electron energy along the axis in the x-direction under different external static magnetic fields

图4 外加静磁场为0.087 5 T时平均电子能量沿轴向分布Fig.4 Distribution of average electron energy along the axis direction when the applied static magnetic field being 0.087 5 T

3.2 微波电场对ECR的影响

在上述模型验证正确的情况下，可以探究微波电场强度与电子轴向速度之间的联系。在图5中给出了外加静磁场为0.087 5 T条件下，微波频率设置成2.45 GHz时x、y、z3个方向的电子速度分布，图6给出了不同微波频率下x方向的电子速度拟合曲线结果与微波电场分布。

图5 微波频率为2.45 GHz时电子速度沿轴向分布Fig.5 The electron velocity distributed along the axial directions when the microwave frequency being 2.45 GHz

图6 不同微波频率下电子速度拟合曲线与微波电场沿轴向分布Fig.6 The electron velocity fitting curve and microwave electric field distributed along the axial direction at different microwave frequencies

从图5中可以得出：共振区域内，电子在z方向的速率并无显著的增加，这是因为系统采用的是TEM波，ECR仅发生在垂直于z轴的方向；而平行于x、y轴的电子在外加静磁场和微波电场的共同作用下沿z轴作震荡运动。模拟中只考察vx作为拟合的曲线结果。

图6考察了1.4、2.45、3.57 GHz 3种条件下的电子速度拟合曲线与微波电场沿轴向分布，仿真中外加静磁场设置为0.087 5 T，可以观察到微波频率取为2.45 GHz时电子共振条件下，电子速度才与微波电场分布趋势相似，而1.4、3.57 GHz微波频率下电子速度与微波电场分布趋势相差很大。且在共振时电子作类似于微波电场周期性变化的震荡运动，说明微波电场推动了电子运动发展。从图6(b)中也可看出，高能电子所在区域总是在微波电场强度较大区域，而随着微波电场强度的降低，电子得到微波电场的加速效果也随之减小。说明在共振区域内，微波电场强度越大，电子的加速效果越明显。

4 结论

采用1D3V模型，对电子回旋共振等离子体的各种物理参量(电子速度、平均电子能量、外加磁场、微波频率)进行数值模拟，结果表明：随着外加静磁场磁感应强度的增加，共振区域内电子的平均能量分布均是先增加后下降，并且在0.087 5 T时达到峰值，同时电子的加速效果也更好，生成的高能电子数量更多。其符合电子回旋频率公式，说明该模型能够进行微波等离子体ECR放电模拟。在0.087 5 T磁感应强度下，微波频率为2.45 GHz时电子共振条件下，电子速度才与微波电场分布趋势相似，说明微波电场推动了电子运动发展。且在共振区域内，微波电场强度越大，电子的加速效果越明显。

综上所述，在微波等离子体ECR放电中可以通过改变微波频率、外加磁场来增加高能电子的产生效率，使电子回旋共振放电产生的等离子体密度和能量转换效率更高。所以利用微波频率、外加磁场等物理参量，可以提高微波等离子体源中高能粒子的产生效率。数值模拟结果也为PIC/MCC方法研究微波等离子体ECR放电规律奠定了基础。