波导阻抗带宽与缝隙导纳关系研究

李 雁, 卢晓鹏, 盛 磊

(中国电子科技集团公司第三十八研究所， 安徽合肥 230088)

0 引言

缝隙波导谐振天线具有效率高、交叉极化低、带内波束指向色散小、功率容量大、机械强度高、环境适应性好等诸多优点，在星载相控阵雷达和通信系统中得到了广泛应用，如国外的TerraSAR-X、Sentinel-1、Almaz-1和国内的海丝1号等SAR系统辐射阵面皆采用了缝隙波导谐振阵。但缝隙波导谐振天线的突出缺点是带宽窄，这限制了它在宽带高分辨军用和民用SAR领域的应用。

为实现缝隙波导谐振阵的宽带设计，很多文献对此进行了研究和讨论。理论上，文献[1]给出了谐振阵的输入驻波比与缝隙数目N及带宽B之间的近似关系。但此关系未计入缝隙间距对工作带宽的影响，同时其计算获得的最大带宽相比工程实践明显偏小。文献[2]从谐振阵等效电路出发，建立了谐振阵实现口径等幅同相激励的理想电纳条件，给出了谐振阵实现方向图最大带宽的导纳设计方向。工程上，公开文献主要从改变缝隙形状[3-4]、子阵化[5-6]和差分馈电[7]等方面探索了展宽缝隙波导阵阻抗带宽的实现方法。其中改变缝隙形状的技术措施会带来交叉极化的恶化以及加工难度的增加。而子阵与差分馈电技术则会带来天线复杂度与厚度的增加。为此希望能从理论上探索出一种实现单层波导谐振阵带宽最大化的分析方法，为阻抗带宽的优化设计提供依据。

本文首先从谐振阵等效网络出发，研究了缝隙谐振阵实现理想阻抗匹配时所需的导纳特性，并建立并联缝隙等效电路，实现缝隙导纳特性的单参数表征，据此提出了一种谐振阵实现最大带宽的导纳特性分析方法，建立了谐振阵不采用过载技术时实现最大带宽的通用公式。同时研究了缝隙宽度对导纳特性与阻抗带宽的影响情况，最后进行了全波仿真设计验证。

1 宽带设计对缝隙导纳需求分析

1.1 理论依据

缝隙波导谐振阵通常采用并联缝隙形式进行设计，以矩形波导宽边开偏置纵向缝为例，其天线模型与等效电路如图1所示。

图1 缝隙波导谐振阵等效电路

对均匀加权缝隙阵，为了简化分析过程，可设yn=y(n=1,2,…,N)，根据微波网络理论，并联电导、短路波导段、并联电导之间波导段以及馈电波导段的T矩阵为

(1)

(2)

(3)

(4)

式中，B为波导的传播常数。由此得到整个网络的T矩阵为

(5)

在缝隙波导谐振阵末端短路的情况下，可推导出端口反射系数为

(6)

(7)

若已知缝隙导纳y，则由式(7)计算端口匹配特性；反之若需要缝隙波导端口匹配，则可取S11=0。通过求解下式方程，得到实现缝隙波导谐振阵宽带理想匹配下各频率点的所需的导纳值。

(8)

1.2 缝隙数对缝隙导纳的影响

工程上缝隙波导谐振阵的最大特点是单根波导上馈电缝隙数越多带宽越窄，首先分析理想匹配情况下缝隙数对缝隙导纳的需求情况。不失一般性，这里以中频5.4 GHz的缝隙波导谐振阵开展实例分析。取d=40 mm=0.72λ0，LS=20 mm，Lf=20 mm，对应矩形波导宽边尺寸a=38.55 mm。由式(8)所列方程求解出不同缝隙数对应的理想归一化导纳曲线，如图2所示。这里的导纳曲线按谐振电导最大值进行归一化处理(以下将此电导、电纳称为归一化电导与归一化电纳)，这是基于Stegen从标准波导孤立单元纵向偏置缝隙大量的测试数据中发现，同一波导口径下，以归一化导纳为纵坐标，以缝隙长度与谐振长度之比为横坐标，不同偏置缝隙的归一化导纳特性基本一致。

(a) 电导特性

(b) 电纳特性图2 理想匹配时不同缝隙数的归一化导纳曲线

由分析结果可见，对于不同的缝隙数，理论上存在对应的导纳特性，可实现裂缝波导谐振天线的理想匹配。缝隙数越少理想匹配时要求归一化导纳变化越平缓，且电纳需求随频率变化具有单调下降趋势。即缝隙数越少，要求缝隙导纳的变化越平缓，谐振性越弱。很容易理解当缝隙数为1时，要求其电导值为1，而电纳值只需要补偿1/4波长短路段引入的电纳。

1.3 缝隙间距对缝隙导纳的影响

工程设计时缝隙单元间距也是需要考虑的设计参数，为此对缝隙数固定且单元间距变化情况下，理想匹配对缝隙导纳的需求情况进行研究。这里以5单元缝隙波导谐振阵开展实例分析，单元间距分别取d=35,40,46 mm，结果如图3所示。可见缝隙间距越大，缝隙的谐振性需求也越强。

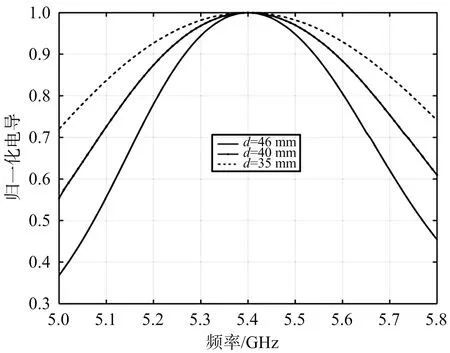
(a) 电导特性

(b) 电纳特性图3 理想匹配5单元线阵不同缝隙间距的导纳曲线

综上，对于特定缝隙数和缝隙间距的波导谐振阵，理论上存在适当的缝隙导纳特性可实现天线端口全带宽的理想阻抗匹配。

2 缝隙等效电路与谐振阵最大带宽

2.1 并联谐振缝隙的等效电路

从物理概念上看，缝隙导纳的频率特性主要由缝隙自身决定，导纳的绝对值由馈电波导的形状及在波导上的偏置决定，这一特性可由Stegen的研究结果所证实。因此，对于特定波导结构的同样缝隙可用一个等效电路进行表征。

根据文献[8]的波导并联缝隙等效电路模型，并参考与缝隙互补的偶极子等效电路[9]，将波导并联缝隙等效为一个RLC串联电路，建立了波导并联缝隙天线单元等效电路，如图4所示。据此可计算出在谐振频率不变的情况下，串联电容变化所引起的天线归一化导纳特性的变化曲线，如图5所示。可见，电容变化将改变天线的频带谐振特性，且电容越大导纳的谐振性越弱。即缝隙导纳的频率特性可用电容C进行计算。

当然，通过职业院校技能大赛，也反映出了我们在教学中的一些薄弱环节。如教学投入不足，教学实习和实训设备不够完善，选手不能适应竞赛中采用的现代企业新设备、新技术、新流程，或在规定时间内完成不了比赛任务；基础理论课教学与专业技能训练没有有机结合。应大力推行教学做一体化模式，使车间与教室合二为一，理论与实践有机融合，努力培养更多高素质、技能型专业人才和实践应用型能工巧匠。

图4 波导并联缝隙天线单元的等效电路

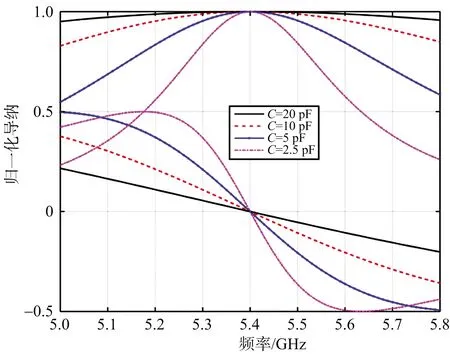
图5 缝隙归一化导纳受串联电容影响的分析曲线

2.2 谐振阵带宽分析方法与可实现的最大带宽

基于图4给出的缝隙等效电路，可建立不同缝隙数、不同单元间距谐振阵获得的最大阻抗带宽的分析方法。具体过程是，针对特定缝隙数的波导谐振阵，通过调整串联电容值，使得导纳特性逼近理想匹配时导纳曲线。然后将此导纳曲线带入公式(7)，分析出此导纳特性下的带内驻波。最后再进一步微调串联电容值，在不采用过载技术的情况下(即中频理想匹配)，优化得到此缝隙数下的最大驻波带宽和对应串联RLC等效电路表征的最优导纳特性曲线。

不失一般性，仍以中频f0=5.4 GHz、dx=40 mm=0.72λ0的缝隙波导谐振阵为例开展分析。采用此方法在最大驻波比分别限定在1.5和2的情况下，得到不采用过载技术时不同缝隙数的谐振阵最大可实现带宽,如表1所示。图6给出最大驻波比为1.5时，不同单元的谐振阵的最优RLC电路导纳特性曲线。可见该曲线与理想匹配情况类似，单元数越少导纳的谐振特性需求也越弱。

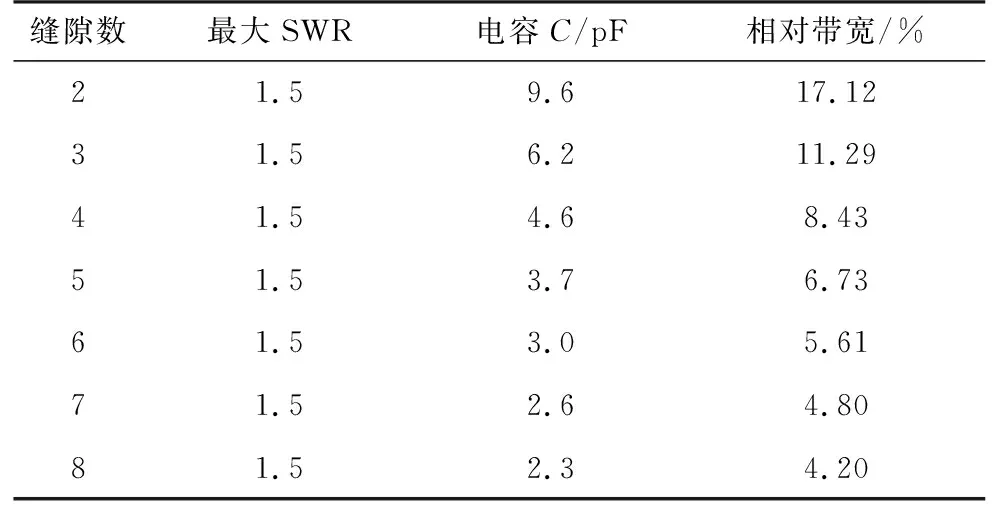
表1 串联RLC电路dx=0.72λ0端馈谐振阵最大带宽

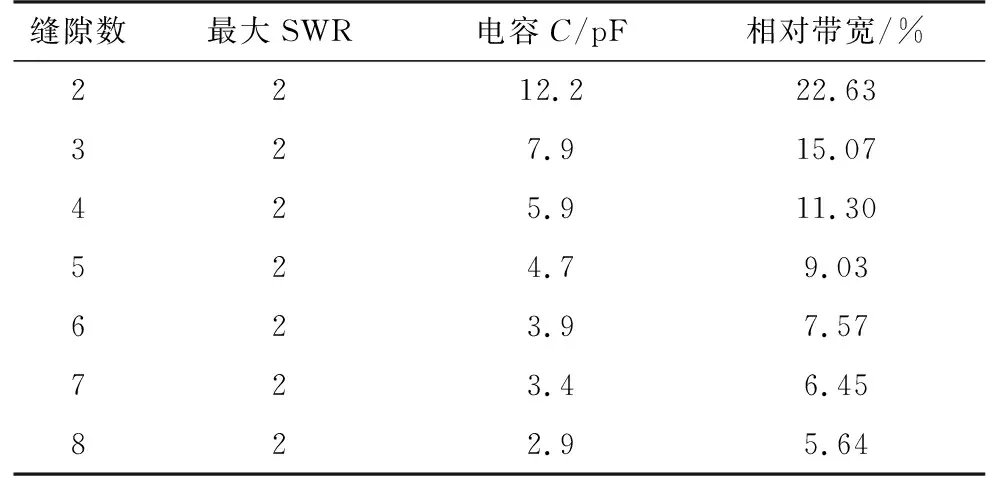
续表

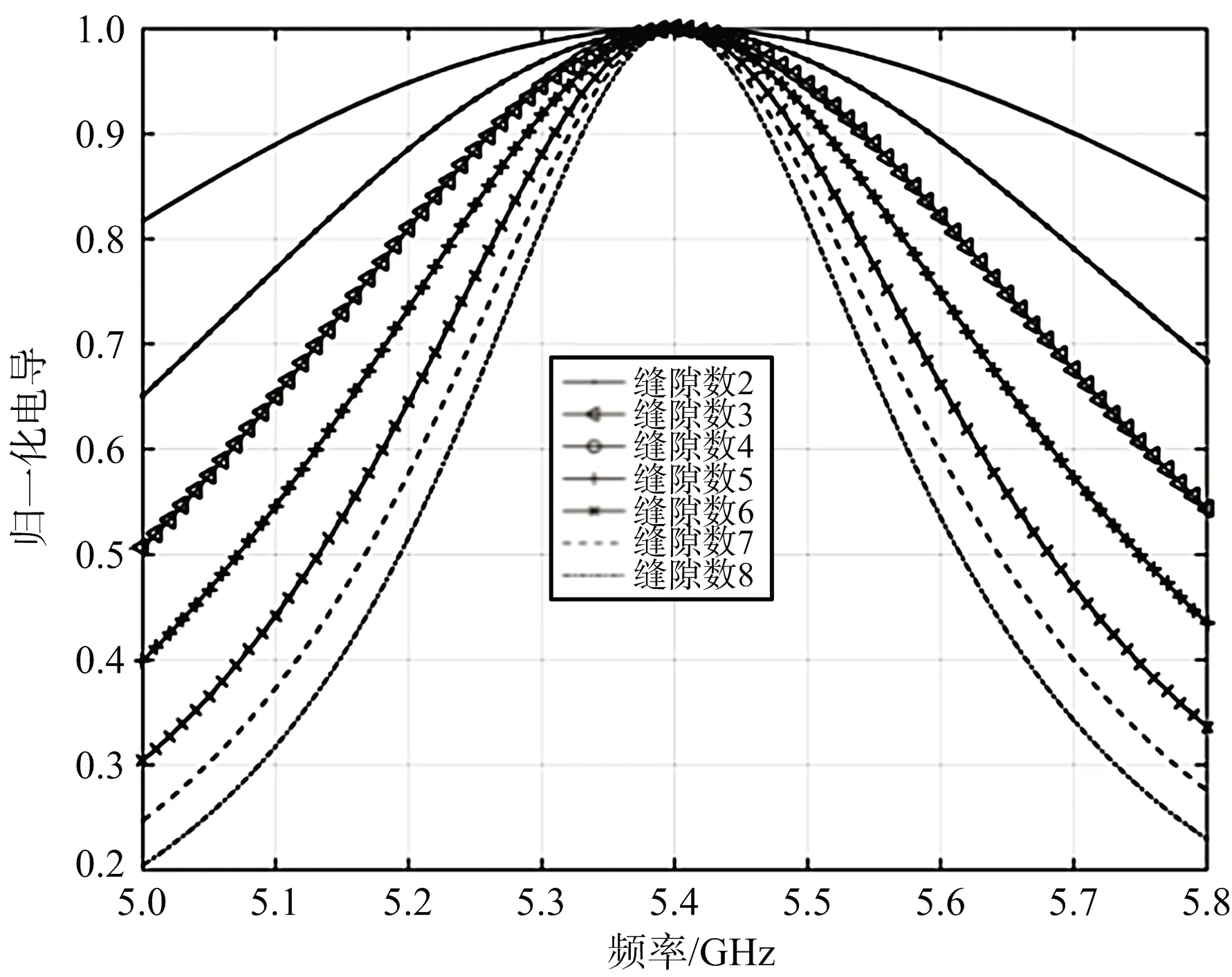
(a) 电导特性

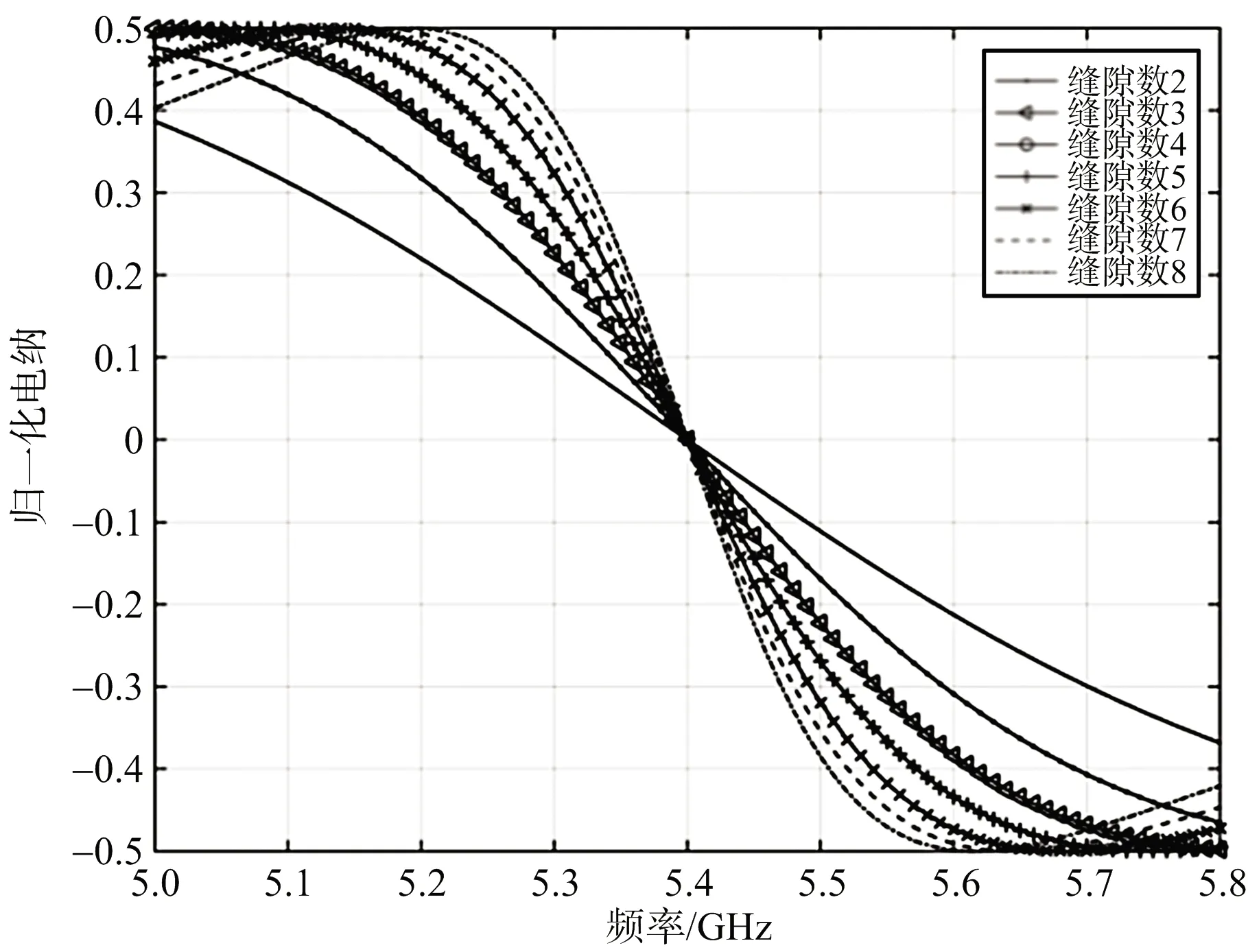
(b) 电纳特性图6 不同缝隙数RLC电路最优导纳曲线

将RLC电路分析出的最大带宽与文献[1]拟合公式的结果进行对比，如图7所示。可见，带宽随单元数的变化趋势两者相同，但同样单元数目的情况下，基于RLC电路得出的天线最大带宽明显优于文献[1]结果。

图7 缝隙数与带宽之间的关系曲线(dx=0.72λ)

由表1还可以看出，不同的最大驻波条件，RLC电路对应的电容不同，为比较这种导纳特性需求差异，以缝隙单元数6为例，图8分别给出了最大驻波比为1.5和2时，带宽最优串联RLC电路的导纳特性与理想匹配时的比较。可见，单纯RLC串联电路无法实现谐振阵全频带的理想匹配，因为RLC串联电路的电导与电纳特性难以同时逼近理想匹配条件，特别是电纳特性在边频远离理想匹配条件。因此串联RLC电路的最优匹配结果是电导、电纳相对于理想匹配条件的折中。此外，允许的最大驻波越大，RLC电路的最优电导曲线越接近理想匹配时的电导曲线。

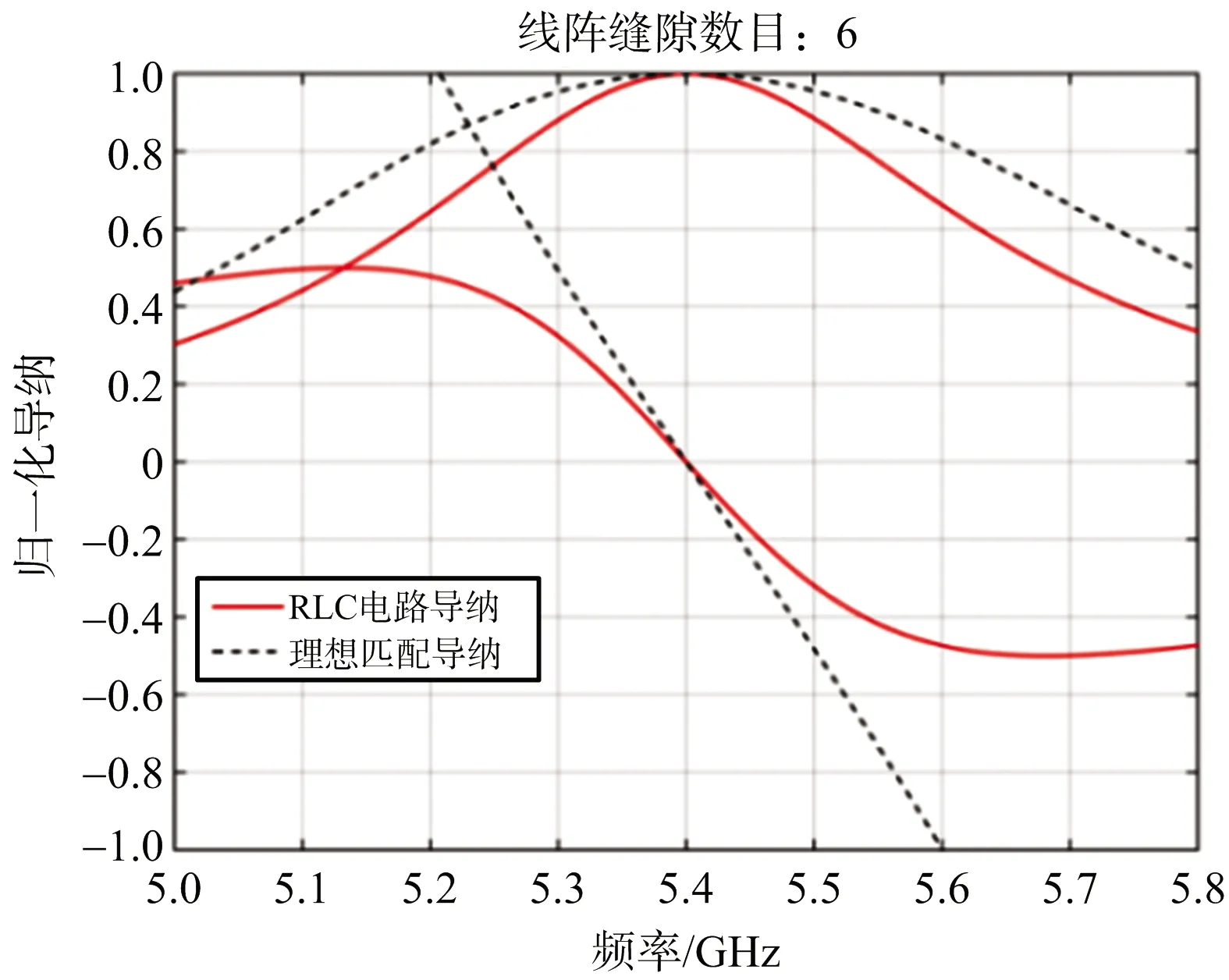
(a) 最大驻波为1.5的导纳

(b) 最大驻波为1.5的带内驻波

(c) 最大驻波为2.0的导纳

(d) 最大驻波为2.0的带内驻波图8 6单元线阵带宽最优时的导纳特性与带内驻波

2.3 不同单元间距可实现的最大带宽

由理想匹配条件分析结果，理想导纳特性与单元间距相关。对不同单元间距谐振阵的最大带宽进行分析，并将相同单元间距不同单元数对应的带宽特性转化成天线长度(单元数×单元间距)与带宽的关系曲线，结果如图9所示。可见，相同谐振阵长度，单元间距越小带宽越大。这表明在谐振阵长度确定的条件下，为实现最大带宽，应尽可能选择小单元间距进行波导谐振阵设计，而不是以缝隙数最少为设计条件。

(a) 最大驻波1.5

(b) 最大驻波2.0图9 不同单元间距的线阵长度与带宽关系

2.4 波导谐振阵最大带宽的拟合公式

根据并联缝隙RLC等效电路模型，对不同缝隙数与不同单元间距的最大带宽进行分析总结，最终获得了不采用过载技术时波导谐振阵最大阻抗带宽的通用公式如下：

(9)

式中，bw为百分比最大相对带宽，λ0为中频工作波长，dx为缝隙单元间距，N为端馈缝隙阵单元数目。

式(9)考虑了缝隙数与缝隙间距的影响，相对等效电路分析结果，带宽计算误差在0.1%以内。

3 矩形波导缝隙宽度对导纳特性与带宽的影响

缝隙波导谐振阵改变缝隙宽度是调整导纳的常见方法，下面对缝隙宽度与导纳特性的关系进行研究，为天线带宽的优化设计提供参考。

3.1 缝隙宽度对导纳特性的影响

取标准矩形波导宽边尺寸a=38.55 mm，b=19.28 mm，d=40 mm。各种缝隙宽度情况下的导纳特性仿真结果如图10所示。可见缝隙宽度越宽，归一化导纳变化越平缓，导纳的谐振特性越弱。但相比于图6所示不同缝隙数的谐振阵所需的最优导纳特性，缝隙宽度的变化只能在有限范围内改变导纳特性。

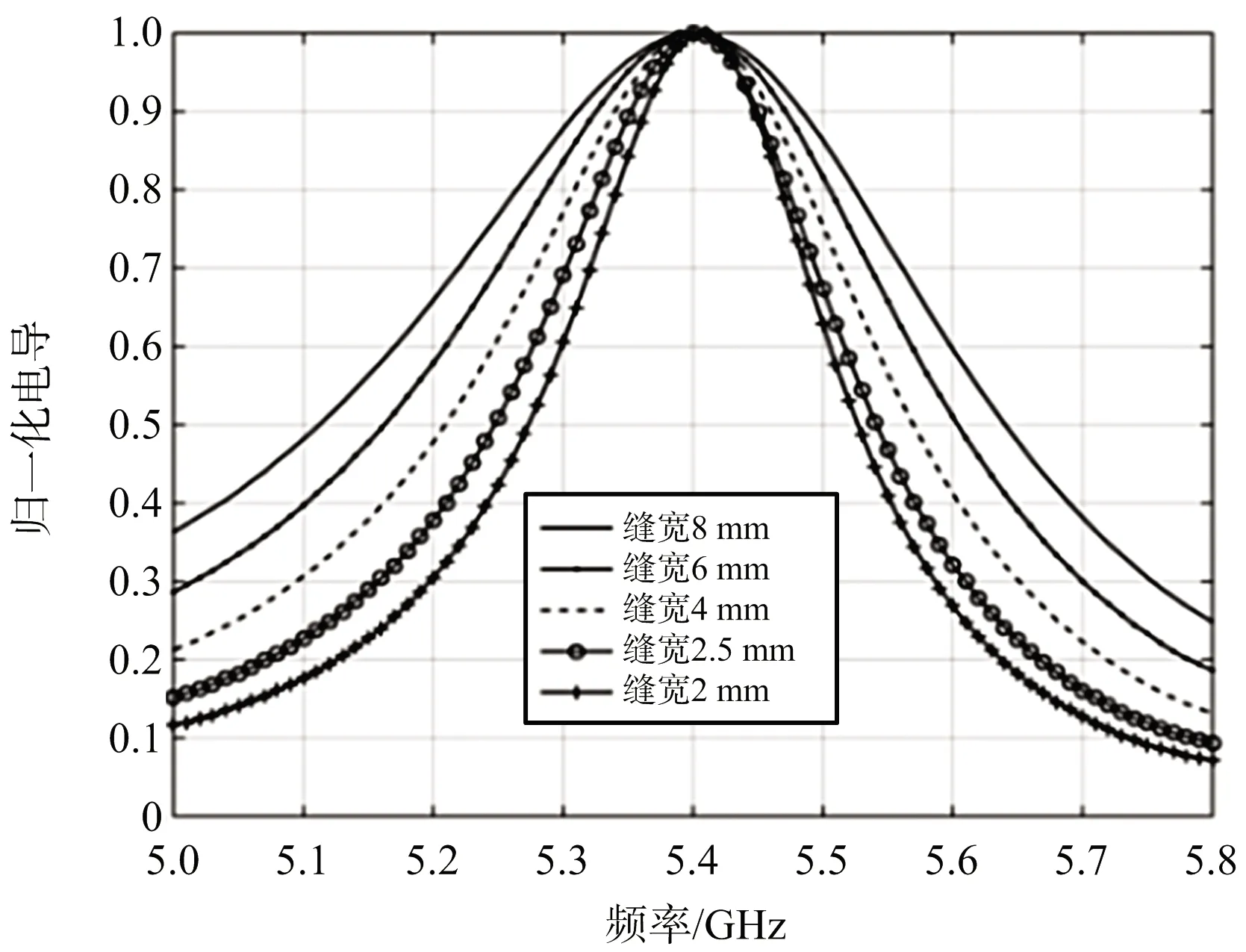
(a) 电导特性

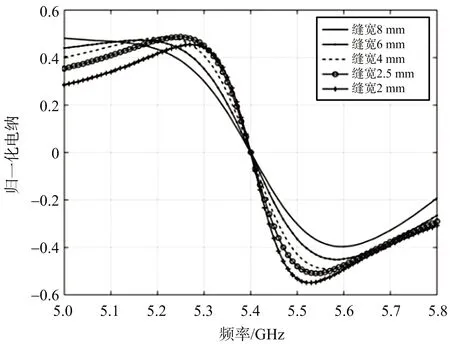
(b) 电纳特性图10 标准矩形波导不同缝隙宽度下的导纳特性

3.2 缝隙宽度对阻抗带宽的影响

为评估缝隙宽度对波导谐振阵带宽的影响，将计算所得的导纳特性代入式(7)，得出缝隙宽度对不同单元数的天线阵的带内驻波性能和带宽的影响情况。结果表明，缝隙数≤5时，通过增加缝隙宽度可明显增加谐振阵的驻波带宽，但当缝隙数>5时，需要选择合适的缝隙宽度来实现带宽的最优化。其中，缝隙宽度对4、8单元线阵端口驻波频率特性影响的分析结果，如图11所示。对于4单元阵，单纯依靠增加缝隙宽度，即使增加到8 mm，驻波比优于1.5时的最大工作带宽仅有6.85%，达不到串联RLC电路所能获得的8.43%最大工作带宽。而在单元数为8时，在所分析的几种缝隙宽度中，宽度为4 mm时驻波比优于1.5的最大带宽约为4.0%，接近4.2%最大工作带宽。

(a) 4单元线阵

可见对于传统矩形波导缝隙天线，在单元数较少的情况下，单纯增加缝隙宽度可展宽工作带宽，但达不到串联RLC电路的理论最大带宽；而在单元数较多时，通过选择合适的缝隙宽度，可获得接近理论分析的最大带宽。

4 设计仿真验证

为验证上述分析结果，以8单元端馈波导谐振阵为设计实例，进行天线的全波仿真验证。此模型采用周期边界进行设计，其中缝隙间距dx=40 mm=0.72λ0，相邻线阵间距dy=39.5 mm，最终优化后的缝隙宽度为5.4 mm，缝隙偏置与长度分别为2.68 mm和25.52 mm，具体模型如图12所示。为补偿宽缝隙所引起的电纳特性所呈现的感性，在模型中引入了宽边容性膜片进行调节，膜片高度Wt=1.28 mm。最终的端口驻波特性优化结果如图13所示，其驻波小于1.5的工作带宽达到了 4.1%，接近等效电路模型最大带宽分析结果4.2%，表明并联缝隙等效电路模型及上述分析结果的正确性。

(b) 天线结构参数图12 8单元线阵周期边界仿真模型

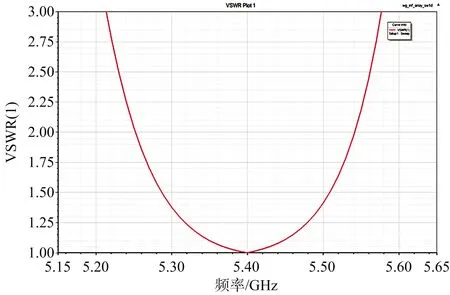
图13 周期边界8单元线阵端口驻波全波仿真结果

5 结束语

本文利用传输线理论，给出了不同单元数、单元间距及缝隙宽度的波导谐振阵实现理想匹配时的导纳频率特性曲线，为后续寻求缝隙谐振阵的全带宽阻抗匹配设计提供了参考。提出了并联缝隙的RLC串联等效电路模型，用单参数串联电容C实现了对缝隙导纳特性的表征，据此建立了分析缝隙波导谐振阵阻抗带宽的新方法，获得了谐振阵实现阻抗带宽最优化所需的导纳特性曲线，为常规波导谐振阵工作带宽的最大化设计确定了导纳优化目标。总结了谐振阵不采用过载技术时，计入单元数与单元间距影响下的最大阻抗带宽的通用公式。并由此得出在波导长度固定的情况下，选择小单元间距有利于增加阻抗工作带宽的结论，为波导谐振阵的布阵优化提供了带宽方面的设计依据。

以标准矩形波导谐振阵为例，研究了缝隙宽度对导纳特性和工作带宽的影响情况，结果表明缝隙宽度可对缝隙导纳特性进行有限范围的调整，在缝隙数较少时，可通过增加缝隙宽度有效提高阻抗带宽，但难以达到RLC电路的理想最大工作带宽；而当缝隙数较多时，可通过选择适当的缝隙宽度实现带宽的最大化。最后，利用全波仿真软件进行了8单元线阵带宽的优化设计，仿真与理论分析结果基本吻合，证明了分析方法和设计过程的有效性。

本文提出的阻抗带宽分析方法，为波导谐振阵带宽的精确设计提供了一种有效手段，具有很好的工程参考价值。后续我们将用此方法对过载技术进行研究，探索采用过载技术时谐振阵的带宽上限。同时还将对不依赖于缝隙宽度变化实现缝隙导纳有效调整的方法进行研究，以实现不同缝隙数的波导谐振阵阻抗带宽的最优化设计。