几何因素对U型管内超临界甲烷流动换热影响

孙鹏 路义萍 韩昌亮 许麒澳 张羽楠

摘 要：超临界甲烷换热器广泛存在于工程实际中，由于超临界甲烷在拟临界温度附近物性变化剧烈，使得其流动与传热规律十分特殊而复杂。基于计算流体动力学（compautational fluid dynamics，CFD）原理，采用有限体积法对超临界甲烷湍流流动与传热特性进行数值模拟，在验证模型可靠性的基础上，分析了弯管曲率半径、U型管立式与水平布置形式对传热特性的影响。结果表明：在管壁边界热流密度q=80kW/m2、入口质量流量G=75kg/（m2·s）、入口温度Tin=180K的条件下，迪恩涡强度随弯管曲率半径的增大而减弱，弯管处的对流传热系数随曲率半径增大而增大;此外，与水平布置相比，U型管立式布置时，超临界甲烷流体与壁面间的对流换热效果更强。本文研究结果对超临界甲烷换热器性能优化具有指导意义。

关键词：超临界甲烷;流动传热;曲率;布置形式

DOI：10.15938/j.jhust.2021.04.018

中图分类号：TK124

文献标志码：A

文章编号：1007-2683（2021）04-0132-06

Abstract：Supercritical methane heat exchangers are widely used in engineering practice. The heat transfer law of supercritical methane is special and compalicated due to the drastic change of physical properties near the pseudo-critical tempaerature. Based on the principle of Compautational Fluid Dynamics（CFD）， the finite volume method is used to simulate the turbulent flow and heat transfer characteristics of supercritical methane. On the basis of verifying the reliability of the model， the influences of curvature radius of bent tube， vertical and horizontal arrangement of U-type tube on the heat transfer characteristics are analyzed. The results show that：when heat flux q=80kW/m2， mass flow G=75kg（m2·s）， and inlet tempaerature Tin=180K， the dean vortex strength decreases with the increase of curvature radius of the bent pipe. The convective heat transfer coefficient at the bent tube increases with the increase of the curvature radius. In addition， compared with the horizontal arrangement， the vertical arrangement of U-type tube has a stronger supercritical methane heat transfer capacity. The results of this paper provide guidance for the performance optimization of supercritical methane heat exchanger.

Keywords：supercritical methane; convective heat transfer; curvature; layout form

0 引 言

液化天然氣是一种清洁的化石能源，从海上运输而来的天然气需加压至其临界压力4.599MPa以上方可应用。 U型管由于其曲型结构被广泛的应用于浸没燃烧式气化器、天然气空温式气化器等气化器。由于甲烷在临界温度附近物性会反生强烈变化。因此，深入研究U型管内超临界甲烷在拟临界温度点附近的流动与传热特性，对液态甲烷气化流程的构建具有重要价值。

目前，国内外对超临界流体介质的研究主要集中在水和CO2的实验和数值模拟上。罗峰等[1]对蛇形管内超临界CO2进行数值计算研究，计算方法对本文U型管的研究具有较大借鉴价值。Xin Du[2]等应用湍流k-ω模型模拟并分析了超临界水，结果表明小管径对换热有加强作用。Mofeng Qu[3]等研究了超临界水传热强化和恶化的机理，确定了边界层比热积分和浮力效应是其主要影响因素。Han[4]对超临界甲烷在水平直管中的模拟得出热传递系数的峰值出现在拟临界点附近。与质量流相比，工作压力对传热性能的影响较小。杨帆等[5]对16mm内径的光滑圆管内超临界压力下低温甲烷的流动与传热进行数值研究，结果表明边界层内的大质量热容和密度差产生的浮升力是传热强化的主要原因。此外还有众多学者讨论了超临界流体在不同条件下的换热关联式[6-8]，文[9-11]使用湍流方程对超临界流体进行数值模拟。

综上，目前超临界流体的实验或数值研究流动传热机理多以CO2或临界水为研究对象。对甲烷的传热规律研究较少，并局限于圆管或特殊通道工况下的研究。本文利用 ANSYS Fluent软件，模拟了甲烷在U形管内的临界流动与换热过程，着重研究甲烷在弯管处于不同曲率对及布置形式对超临界甲烷在弯管处对流动换热的影响。

1 模型及求解与验证

1.1 物理模型

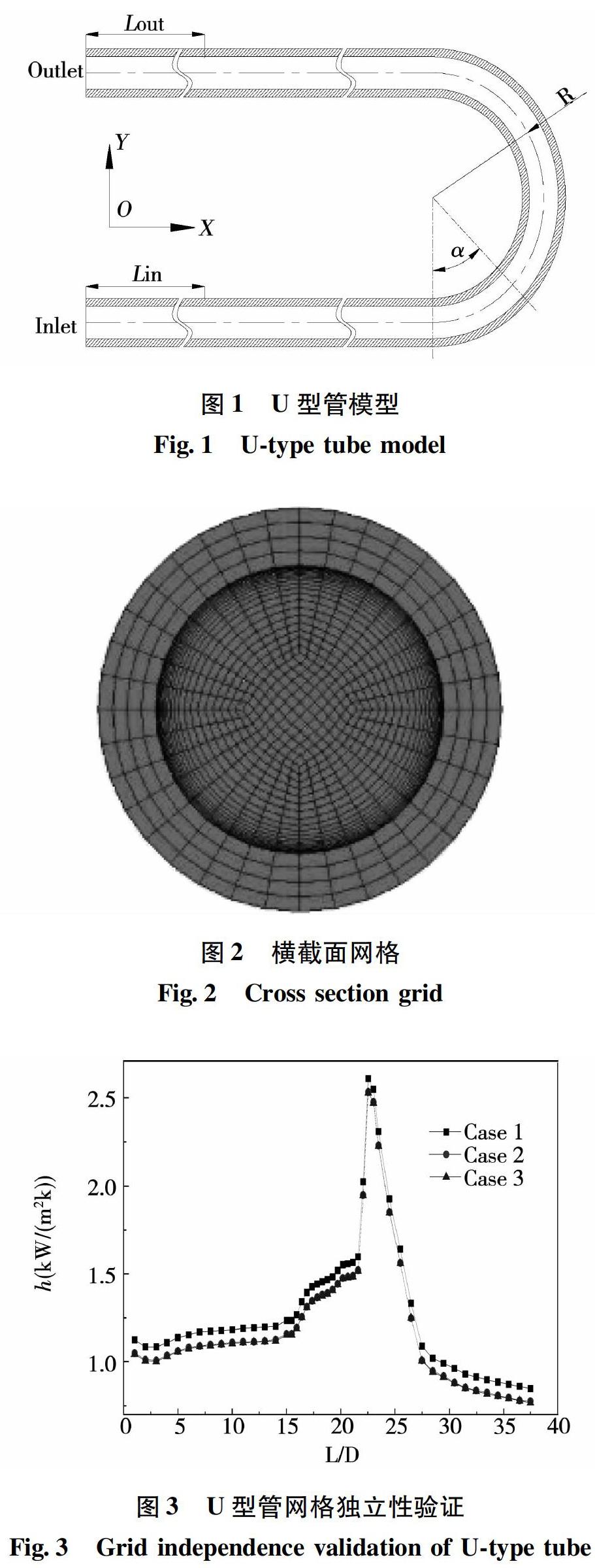
本文三维U型管物理模型如图1，其尺寸为：管壁厚度为δ=2mm，圆管内径为D=10mm，U型管曲率为R=27mm，管道总长度为1580mm，其中加热段长度为380mm，此外模型还设有长度为600mm的入口段Lin和出口段Lout。

1.2 网格划分及独立性验证

对近壁面网格进行加密处理，在保证近壁面边界层区域内第一层边界层高度满足y+<1，之后按1.2的比例逐渐增大横截面网格见图2。将3组U型管离散网格（网格数分别为140万、170万、200万）进行独立性验证，监测管表面对流换热系数h这一主要物理量沿管长方向的变化情况，见图3，由图3可知，随网格数量增加，Case 2和Case 3的h曲线基本重合，最终选用Case 2的网格设置。

1.3 数学模型及求解条件

在本次计算中，忽略流体与外界环境之间的换热、仅分析热流边界条件中热流密度对流体的影响，同时考虑重力影响。管内流动和换热过程服从质量守恒定律、动量守恒方程和能量守恒方程，其通用控制方程见式（1）。所有工况条件下的Re均远大于临界值，流动处于湍流状态，Realizable k-ε模型可以准确计算管道的分离的流动，湍流模型采用Realizable k-ε模型，见式（2）、（3）。由于本文仅研究稳态，故方程均忽略时间项。

式中：ρ为密度;U是流体流动的速度矢量;ui为速度在3个坐标方向的分量;φ为通用控制变量;Γ为广义扩散系数;S为带有重力项的广义源项;k为湍流脉动动能;Gk为浮升力项;ε为湍流脉动动能耗散率;C1、C2为常数σε、σk分别为k和ε的湍流普朗特数。

本文在应用FLUENT软件进行求解时，把甲烷物性看作温度的单值函数计算，在压力P=6.93MPa下的甲烷物性见图4。具体工况条件为：流体入口为质量流量进口，G=75kg/（m2·s），入口温度Tin=180K，热流密度q=80kW/m2、重力g=-9.8m/s2，流体出口为压力出口，压力P=6.93MPa。求解压力与速度离散方程组耦合采用SIMPLE算法，动量和能量采用二阶迎风格式进行离散。

1.4 模拟准确性验证

为说明湍流模型对计算结果的准确性影响，利用Realizable k-ε模型数值模拟了文[12]中的实验结果。本文对该实验进行建模并数值模拟，与文献的记过偏差见图5，具体为焓值和对流换热系数的变化关系，结果表明二者的平均误差为 9.1%，证明了本文计算模型的正确性。

2 U型管布置形式对传热特性的影响

迪恩涡是流体在曲率作用下，使管内速度场、压力场发生变化的现象，将迪恩涡对流和剪切作用应用到传热领域，可以显著地提高换热系数[13]，其强度可由迪恩数衡量。 迪恩数（Dn）表达式见式（4），其中Re为雷诺数，r为管徑，R为弯管处的曲率半径。

本节介绍了水平U型管（xoy面平行于水平面）和立式U型管（xoy面垂直于水平面，入口在下）对换热的影响。图6为水平U型管和立式U型管两种布置形式下管壁温度Tw和对流换热系数h随L/D的变化规律，由图6可知，前半段水平U型管与立式U型管的Tw变化曲线相近，因此进入弯管前的直管段不会因水平或垂直的布置方式对换热产生影响。当流体处于弯管之中的前一刻，壁面温度Tw存在一个小幅下降的趋势，在此之后Tw则逐渐升高。相同时刻的流体在流出弯管后壁面温度会出现降阶式的突降，而后Tw则会换换增大，但这一上升趋势是沿着L/D方向增大的，也是随着加热的不断进行而产生的。

此外，L/D=27.5是U型管水平布置与立式布置的换热系数的一个分界点，处在27.5之后的位置立式U型管的换热系数要比水平U型管小，这说明水平管的换热效果更好。而L/D在15～27.5范围立式管的换热强度更大。之所以会有这样的效果出现是因为在L/D=27.5之前，立式管换热强度大，并且已经将流体温度升高至拟临界温度以上，导致物性变化平稳并使密度差降低，从而浮力效应减弱换导致换热强度降低。此外，立式U型管在弯管处的换热效果有明显的提升。

图7为水平U型管和立式U型管的Dn随弯曲角度α的变化规律。由图7可知，在水平U型管中，的Dn数与弯曲角度α正相关，在弯曲通道出口处（α=180°的位置），Dn数出现最大值。当α<170°时，立式U型管的Dn数高于水平U型管。

3 曲率半径对传热特性的影响

图8为曲率半径R分别为17mm、27mm、37mm时，在原始计算条件下超临界甲烷在U型管内的壁面温度Tw、对流换热系数h随L/D的变化情况。由图8可知，流体进入弯管前，不同曲率半径对应的Tw变化规律相同，总体呈先升高再下降后升高的趋势，三条曲线基本重合，说明曲率半径的改变对流体进入弯管前的换热影响较小，流体进入弯管后，R=27mm、R=37mm条件下的Tw先下降后升高，曲线出现谷值。随着曲率半径的增大，谷值点左移。且当R =17mm时，Tw在L/D=21处出现峰值。工质流体离开流出弯管后，可以看出不同当改变曲率半径条件时，不同曲线所对应下的Tw出现了存在交点。尤其是位于在加热段出口的附近区域，3条曲线存在明显差异间的差异较为显著，但整体趋势大致相同，Tw随着曲率半径的增大，而h逐渐减小。

从由图8可知，当R=17mm时，h的谷值出现在L/D =21处，说明在该位置处出现换热的恶化现象。然而通过提升U型管对应的曲率半径，这一换热恶化现象明显得到改善。同时还可以看到，在R=27mm、R=37mm条件下的h同样呈现出先升高后降低的趋势下降，两种h曲线的峰值点与Tw曲线的谷值点相对应。同时，当曲率半径由R=17mm增至R=37mm时，h的峰值减小约17%。这是由于因为在保持管道的长度总长不变的前提下，增大曲率半径，会导致直管段长度减少，因此近壁面流体在进入弯管前后还未才达到拟临界温度，当流体刚进入弯管后时，浮升力效应以及和迪恩涡强度都逐渐得到了显著的增强，同时h随着曲率半径的增长增大而升高增大。随着加热的进行，浮力效应和迪恩涡强度减小，h下降，h峰值点移动方向与迪恩涡的峰值点移动方向一致。

圖9为不同曲率下的迪恩数Dn随弯曲角度α的变化规律，由图9可知，改变不同曲率半径对于下的Dn的分布并未产生显著影响，其变化规律趋近相同，Dn均为先升高后降低。在当R=17mm时， 27mm，37mm时，峰值分别出现在α=160°、α=130°， α=110°的对应位置。随着曲率半径逐渐的增大，Dn开始降低且其峰值点出现左移现象，同时弯管出口的h也随之增大，说明说明迪恩涡的强度将随着曲率半径的增加而降低，进一步证明了对于延长弯管的延长将有利于整体的换热冷却效果。此外，当R=17mm时，由于近壁面流体在进入弯管前已达到拟临界温度，流体进入弯管后所受到的浮力效应逐渐减弱变缓，迪恩涡的强度逐渐升高并恶化了换热。随着U型管曲率半径的增大，可以观察到迪恩涡强度逐渐降低减小，换热恶化现象得到了明显改善。

4 结 论

1）迪恩涡对于弯管对流的换热能力具有十分显著的影响，同时在弯管内对流换热系数h与迪恩涡的强度的变化规律趋近一致，均为先升高后降低，且在弯管位置处可以观察到h的峰值;随着曲率半径的增大，h和迪恩涡的峰值减小，R=17mm时，弯管内发生换热恶化。

2）在流体进入弯管前，U型管的布置形式对于之前的直管段换热并无显著影响，而当流体进入弯管后，可以观察到立式U型管的换热能力明显强于同一工况条件下的水平U型管;而当流体由弯管流出再一次进入后续直管段时，水平U型管整体的温度低于立式U型管，说明此时水平布置方式的换热能力较强。以上结论证明了与水平U型管相比，立式U型管可以抑制流体在弯管段内的换热恶化，而水平U型管则可以改善其在水平段内的流动换热。

3）工质在U型管中的流动换热可分为水平直管段、弯管段以及后续水平直管段三部分。其中弯管段的存在并未对水平直管段内的流动换热造成显著影响，该位置处的换热特性与水平直管大体一致，但导致了后续水平直管段内的换热恶化;工质流入弯管后，其强度先增大后减小;期间流体在弯管靠近外壁附近区域形成低速低温区，在内壁附近区域形成相应的高速高温区;工质的对流换热系数h在进入弯管后得到了较为明显的增长，随后便随着流动逐渐降低。

参 考 文 献：

[1] 罗峰， 胥蕊娜， 等. 细蛇形管内超临界压力CO_2层流对流换热数值研究[J]. 工程热物理学报， 2014， 35（6）：1170.

LUO Feng， XU Ruina. Numerical Investigation on Laminar Convection of Supercritical Pressure CO2 in a Mini Serpentine Tube[J]. Journal of Engineering Thermophysics，2014， 35（6）：1170.

[2] DU Xin， LV Zhihao， ZHAO Shuai， et al. Numerical Analysis of Diameter Effects on Convective Supercritical Water Flow in a Vertical Round Tube[J]. Applied Thermal Engineering， 2019， 160：14095.

[3] QU Mofeng， YANG Dong， LIANG Ziyu， et al. Experimental and Numerical Investigation on Heat Transfer of Ultra-supercritical Water in Vertical Upward Tube under Uniform and Non-uniform Heating[J]. International Journal of Heat and Mass Transfer， 2018， 127：769.

[4] HAN Changliang， ZHANG Yunan， YU Hong， et al. Numerical Analysis on Non-uniform Flow and Heat Transfer of Supercritical Cryogenic Methane in a Heated Horizontal Circular Tube[J]. The Journal of Supercritical Fluids， 2018， 138：82.

[5] 杨帆， 刘畅， 姜文全， 等. 超临界压力下低温甲烷传热特性数值研究[J]. 中国石油大学学报（自然科学版）， 2018， 42（6）：139.

YANG Fan， LIU Chang， JIANG Wenquan， et al. Numerical Study of Cryogenic Methane Heat Transfer Characteristics under Supercritical Pressure[J]. Journal of China University of Petroleum， 2018， 42（6）：139.

[6] GU Hongfang， LI Hongzhi， WANG Haijun， et al. Experimental Investigation on Convective Heat Transfer from a Horizontal Miniature Tube to Methane at Supercritical Pressures[J]. Applied Thermal Engineering， 2013， 58（1/2）：490.

[7] LIU Z B， HE Y L， QU Z G， et al. Experimental Study of Heat Transfer and Pressure Drop of Supercritical CO2 Cooled in Metal foam Tubes[J]. International Journal of Heat and Mass Transfer， 2015， 85：679.

[8] WANG K Z， XU X， LIU C， et al. Experimental and Numerical Investigation on Heat Transfer Characteristics of Supercritical CO2 in the Cooled Helically Coiled Tube[J]. International Journal of Heat and Mass Transfer， 2017， 108：1645.

[9] 崔海亭， 刘思文， 王少政. 超临界CO2水平直管内冷却换热的数值模拟[J]. 河北科技大学学报， 2019， 40（3）：2528.

CUI Haiting， LIU Siwen， WANG Shaozheng. Numerical Simulation of Convection Heat Transfer of Supercritical Carbon Dioxide in Horizontal Straight Tube[J]. Journal of Hebei University of Science and Technology， 2019， 40（3）：252.

[10]靳书武， 武锦涛， 银建中. 水平圆管内超临界甲烷对流换热数值模拟[J]. 应用科技， 2015， 42（5）：67.

LE Shuwu， WU Jintao， YIN Jianzhong. Numerical Simulation of Convective Heat Transfer of Supercritical Methane in a Horizontal Tube[J]. Applied Science and Technology， 2015， 42（5）：67.

[11]HAN Changliang， REN Jingjie， WANG Yanqing， et al. Numerical Investigation of Supercritical LNG Convective Heat Transfer in a Horizontal Serpentine tube[J]. Cryogenics， 2016， 78：1.

[12]LEI Xianliang， ZHANG Jun， GOU Lingtong， et al. Experimental Study on Convection Heat Transfer of Supercritical CO2 in Small Upward Channels[J]. Energy， 2019， 176：119.

[13]湛含輝， 朱辉， 陈津端， 等. 90°弯管内二次流（迪恩涡）的数值模拟[J]. 锅炉技术， 2010， 41（4）：1.

ZHAN Hanhui， ZHU Hui，CHEN Jinrui， et al. Numerical Simulation of Second Flow（dean vortices） in 90°Curved Tube[J]. Boiler Technology， 2010， 41（4）：1.

（编辑：温泽宇）