基于测量不确定度计算冻猪肉中挥发性盐基氮的误判概率

郭 胜，凌 霞，李文慧，杨 莹

（襄阳市公共检验检测中心，湖北 襄阳441000）

在检验检测中会出现测量结果处于容许限附近的情况，对于此类测量结果的符合性判定，CNASGL015:2018《声明检测或校准结果及与规范符合性的指南》[1]附录A给出了10种可能出现的情况。若采用最为常用的二元决策判定，即判定结论只有合格与不合格两种情况，当测量结果处于“情况2、情况3、情况4、情况7、情况8、情况9”时存在错误接受或错误拒绝的风险。

CNAS-CL01:2018《实验室认可指南》[2]中的“7.8.6.1”条款规定：“当做出与规范或标准符合性声明时，实验室应考虑与所用判定规则相关的风险水平（如错误接受、错误拒绝以及统计假设），将所使用的判定规则制定成文件，并应用判定规则”。CNASTRL-010:2019《测量不确定度在符合性判定中的应用》[3]中的“4.3”条款对错误接受、错误拒绝等进行了具体定义。当符合性判定结论处于错误接受或者错误拒绝时存在误判的风险，通过对误判概率的计算，得到一个具体的量化概率值来准确评价符合判定的风险水平。

挥发性盐基氮是肉类食品储存过程中蛋白质的分解产物，是衡量肉制品新鲜程度的重要指标[4-6]，已成为猪肉新鲜程度的标准检测法[7]。在猪肉冷冻保存过程中，挥发性盐基氮含量有逐渐升高的趋势[8-9]，因此对冻猪肉检测挥发性盐基氮是很有必要的。本文以一次测量结果处于容许限附近的冻猪肉中挥发性盐基氮的检测为例，对误判概率的计算详细展开。目前还没有针对误判概率进行详细计算的具体实例，本文对检验检测领域的误判概率计算具有一定的参考意义。

1 材料与方法

1.1 材料与设备

1.1.1 材料与试剂

冻猪肉：监督抽检样品；氧化镁，南京化学试剂股份有限公司；硼酸，西陇科学股份有限公司；盐酸标准溶液（浓度C0=0.100 2 mol/L，U=0.000 2 mol/L，k=2），北京坛墨质检科技股份有限公司；甲基红指示剂，天津市科密欧化学试剂有限公司；溴甲酚绿指示剂，国药集团化学试剂有限公司；95%乙醇，西陇科学股份有限公司。以上试剂均为分析纯。

1.1.2 仪器与设备

BSA224S型电子天平，赛多利斯科学仪器（北京）有限公司；UPYZX-11-10型纯水机，四川优普超纯科技有限公司。

1.2 方法

1.2.1 试样处理

称取制备均匀的冻猪肉试样20 g于具塞锥形瓶中，用量筒加入100.0 mL水，振摇使试样分散均匀，浸渍30 min后过滤。

1.2.2 测定方法

依据GB 5009.228—2016《食品安全国家标准 食品中挥发性盐基氮的测定》[10]第一法中步骤“5.3”对冻猪肉样品平行测定6次。

1.2.3 结果的计算与表述

试样中挥发性盐基氮含量的计算公式如下：

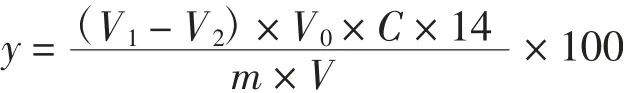
式中：y为挥发性盐基氮含量，mg/100 g；V1为试液消耗盐酸标准滴定使用液的体积，mL；V2为空白消耗盐酸标准滴定使用液的体积，mL；C为盐酸标准滴定使用液的浓度，mol/L；14为1.0 mL盐酸[C（HCl）=1.000 mol/L]标准滴定溶液相当的氮的质量；m为试样质量，g；V为吸取滤液体积，mL，本次检验中V=10 mL；V0为样液总体积，mL，本次检验中V0=100 mL。

1.3 评定误判概率

依据JJF 1059.1—2012《测量不确定度评定与表示》[11]评定测量不确定度，查询冻猪肉产品标准得出挥发性盐基氮容许上限TU。将测量结果y、容许上限TU、合成标准测量不确定度u代入CNAS-TRL-010:2019[3]中的合格概率计算公式，计算样品的合格概率。依据CNAS-GL015:2018[1]进行符合性判定，由合格概率结合符合性判定结论得出误判概率。

2 结果与分析

2.1 挥发性盐基氮测量结果

对冻猪肉试样平行测定6次，测定结果见表1。

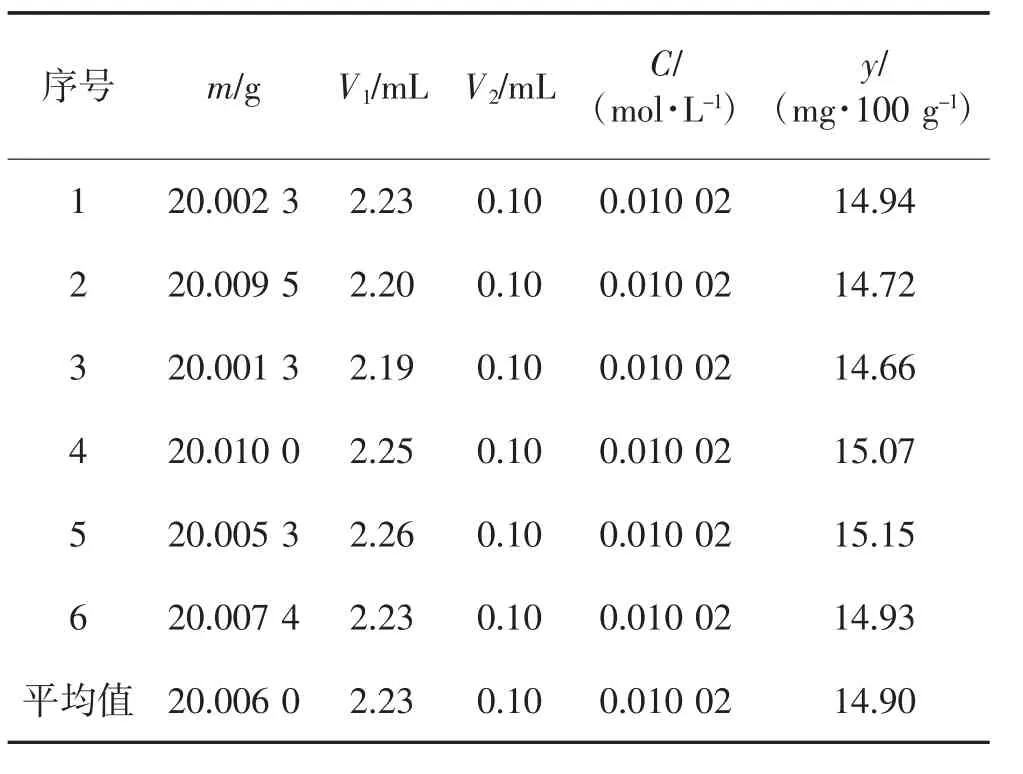
表1 挥发性盐基氮的测定结果Table 1 Determination results of TVB-N

2.2 评定测量不确定度

2.2.1 不确定度来源分析

分析检验过程和数学模型，挥发性盐基氮的测量不确定度主要来源见图1。

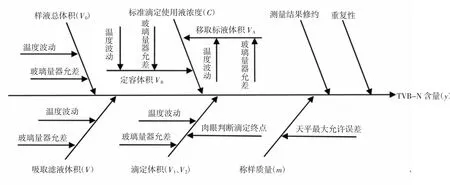
图1 冻猪肉中挥发性盐基氮的不确定度来源Fig.1 The uncertainty sources of TVB-N in frozen pork

2.2.2 测量重复性引入的不确定度分量ux¯（y）[12-13]

6次测定结果平均值为14.9 mg/100 g，带入标准偏差计算公式得：测量重复性引入的不确定度：

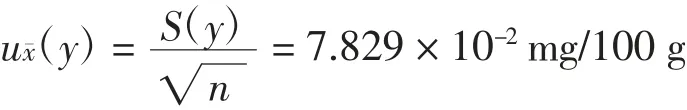
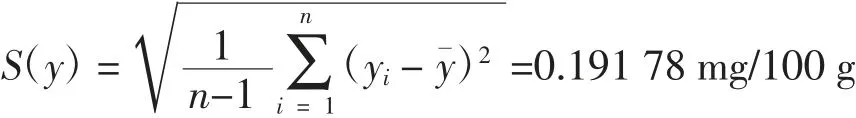
2.2.3 由体积V、V0、V1、V2引入的不确定度分量

记录整个试验过程，实验室温度波动范围为（20±3）℃，水的膨胀系数为2.1×10-4/℃，假设为矩形分布[14]。

本次滴定在临近滴定终点时再加半滴盐酸标准滴定液，溶液颜色就有很明显的变化，肉眼足以分辨，所以肉眼判断滴定终点引入误差的半宽度取半滴定液的体积约为0.03 mL，假设为矩形分布。

体积V1与体积V2是由10 mL A级滴定管的滴定体积；体积V是由10 mL A级单标线移液管移取的体积；体积V0是由100 mL A级量筒量取的体积。查询JJG 196—2006《常用玻璃量器检定规程》[15]得出玻璃量器允差的半宽度，假设为三角分布[16-17]。由体积V、V0、V1、V2引入的不确定度分量见表2。

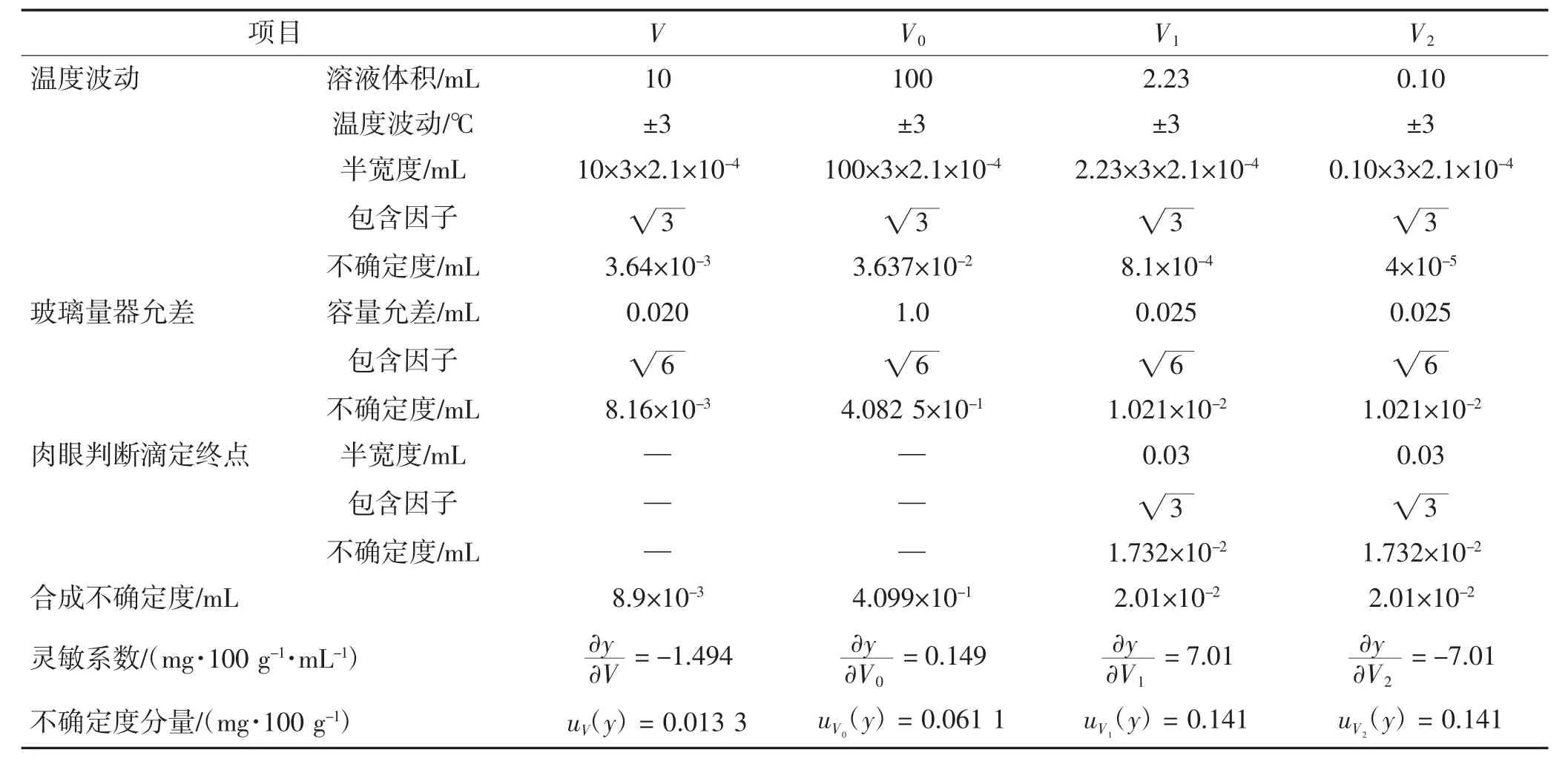
表2 由体积V、V0、V1、V2引入的不确定度分量Table 2 Uncertainty components introduced by volumes V，V0，V1 and V2

2.2.4 盐酸标准滴定使用液浓度C引入的不确定度uC（y）

盐酸标准滴定使用液的稀释步骤如下：用10 mL移液管（A级，单标线）移取10 mL盐酸标准溶液至100 mL容量瓶（A级）中，以纯水定容。

盐酸标准滴定使用液浓度的计算公式为：

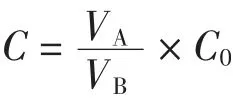
式中:C为盐酸标准滴定使用液浓度，mol/L；VA为移液管移取盐酸标准溶液的体积，mL；VB为定容体积，mL；C0为盐酸标准溶液浓度，mol/L。

查看盐酸标准溶液的标准物质证书得知其扩展不确定度U=0.000 2 mol/L，k=2。

盐酸标准溶液浓度C0引入的标准不确定度：

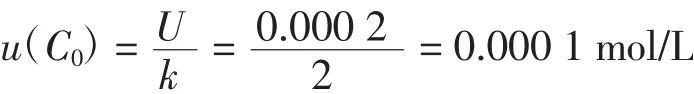
盐酸标准滴定使用液浓度C引入的不确定度见表3。

表3 由盐酸标准滴定使用液浓度引入的不确定度Table 3 Uncertainties introduced by concentrations of hydrochloric acid standard titration solution

盐酸标准滴定使用液浓度C引入的合成标准不确定度：

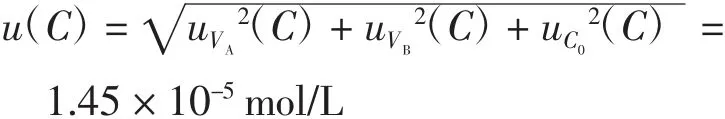
盐酸标准滴定使用液浓度C的灵敏系数：

由盐酸标准滴定使用液浓度C引入的不确定度分量：

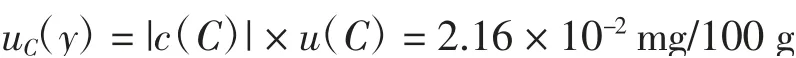
2.2.5 称样质量m引入的不确定度分量um（y）[18]

查阅天平检定报告，称样所用天平在称样量小于50 g时，最大误差为±0.5 mg，假设为矩形分布则称量质量引入的标准不确定度：

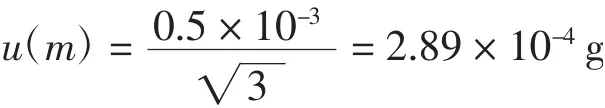
称样质量m的零敏系数：

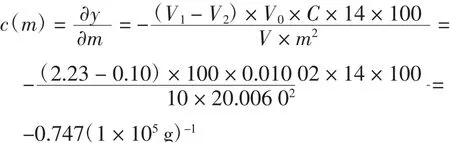
称样质量m引入的不确定度分量：

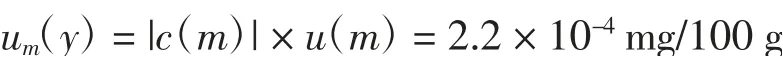
2.2.6 测量结果修约引入的不确定度分量uA（y）[19]

GB 5009.228—2016[10]规定计算结果保留3位有效数字，测量结果修约为14.9 mg/100 g，其修约间隔为0.1 mg/100 g，修约半宽度为0.05 mg/100 g，假设为矩形分布则结果修约引入的不确定度分量为：

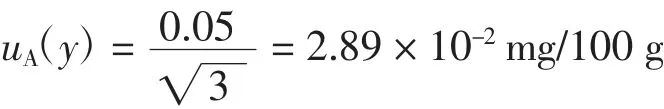
2.2.7 综上所述，挥发性盐基氮含量的合成标准不确定度为：

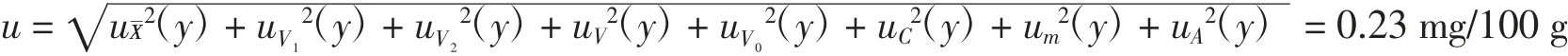
2.2.8挥发性盐基氮含量的扩展不确定度

取扩展因子k=2（置信概率95%）,扩展不确定度：U=2×0.23=0.46 mg/100 g。

2.3 计算合格概率

GB 2707—2016《食品安全国家标准鲜（冻）畜、禽产品》[20]规定冻猪肉中挥发性盐基氮含量≤15 mg/100 g，即容许上限TU=15 mg/100 g。

根据中心极限定理，结合测量不确定的评定过程，得出试样中挥发性盐基氮测量结果的概率密度函数近似服从正态分布[21-22]，依据CNAS-TRL-010:2019[3]中容许区间为单一容许上限区间的合格概率公式求得合格概率：

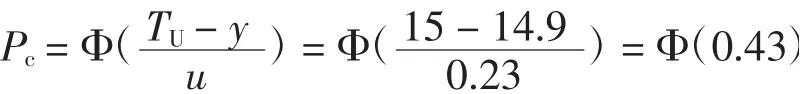
查询标准正态分布表[22]得合格概率Pc=66.6%。

2.4 进行符合性判定

测量值y=14.9 mg/100 g小于容许上限，测量值y加上扩展不确定度U=15.36 mg/100 g大于容许上限。在进行符合性判定时属于CNAS-GL015:2018[1]附录A中的“情况2”。规范要求在证书或报告中做出符合性声明时，本次检验的符合性判定结论可报告为：合格（包含概率可以低于95%的情况下）。

2.5 评定误判概率

若采用二元决策判定，本次符合性判定可判定为合格，但在考虑测量不确定度时，真值依然有一定的概率落在容许区间以外，即有一定不合格概率。依据CNAS-TRL-010:2019[3]中的“7.3”条款中二元决策的符合性评价可能出现的结果，本次符合性判定结论有一定的概率处于无效合格状态。

CNAS-TRL-010:2019[3]中的“7.3”条款关于无效合格的表述：“产品目标属性的符合性判定结论合格，但不符合客观事实。这种错误结论将残次品判断为合格品并出售给消费者，带来的损失通常由消费者承担，因此这种误判称为消费者风险。在实际符合性判定活动中依据被测量的测得值得到的满意结果时，得到无效合格结论的概率称为特定消费者风险，符号为RC*，RC*=1-Pc。”由此可知，特定消费者风险就是误判风险，即本次检验的误判概率。

试样中挥发性盐基氮含量的合格概率Pc=66.6%。所以本次检测符合性判定的误判概率为:P=RC*=1-Pc=33.4%。

3 结论与讨论

本次误判概率计算，当容许上限TU=15 mg/100 g，测量值y=14.9 mg/100 g，标准测量不确定度u=0.23 mg/100 g，符合性判定结论为合格时，符合性判定的误判概率为33.4%。

本次检验测量值处于容许限以内，测量值加上测量不确定度后处于容许限以外，符合性判定为合格时，误判概率P=RC*=1-Pc。在检验检测中符合性判定存在误判的另一种情况是，测量值处于容许限以外，测量值加上测量不确定度后处于容许限以内，此时采用二元决策判定，可判定为不合格，但依然有一定的合格概率。依据CNAS-TRL-010:2019[3]中的“7.3”条款，此时符合性判定有一定概率处于无效不合格状态。这种错误结论将合格品误判为残次品，使生产商无法售出合格品，带来的损失由生产商承担，因此这种误判称为生产商风险。实际符合性评价中依据被测量的值得到不满意结果时，得到无效不合格结论的概率称为特定生产商风险，表示为RP*，RP*=Pc。由此可知特定生产商风险就是误判风险，即误判概率，此时误判概率P=RP*=Pc。