计算小于任给整数的素数个数的一个近似

唐军强

（焦作大学基础部，河南 焦作 454000）

素数的分布是一个古老的问题。素数有无穷多个，古希腊数学家欧几里得在公元前 300 年左右就给出了一种简洁的证明。而欧拉使用“埃拉托色尼筛法”给出的一个式子——今天我们称为欧拉乘积公式，揭示了黎曼函数与素数分布之间的一种天然的联系[1]

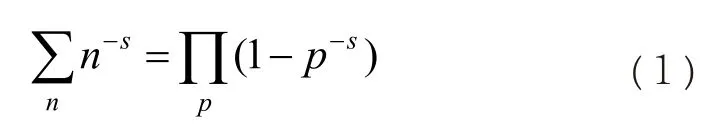
等式左端为对所有的正整数求和，等式右端为对所有的素数求积。当s=1时，左端级数发散，这提供了素数没有穷尽的另一个证明。黎曼 1859 年的论文《论小于一个给定值的素数的个数》正是从(1)式出发，给出了一个准确的关于的式子[2]，同时提出了举世闻名的黎曼猜想，即黎曼函数的所有非平凡零点的实部都是，至今未能获得证明。依赖于素数特性的现代密码编制术和破译术，其根基就在这里。而二十世纪的一系列非凡进展，显示出甚至原子物理学都尚未被完全理解的方式与这个奇怪难题扯上了关系。但是，黎曼假设是比素数定理更强的条件，即使没有黎曼假设的成立作保证，人们依然证明了素数的分布服从[3]

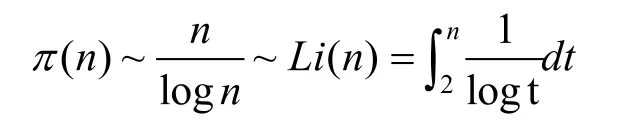
1.公式的推导

该公式的推导灵感来自于数论中欧拉公式的一种初等证明[4]，代表小于n且与之互素的自然数的个数，包括1在内。它的计算公式是

(2)式中 为n的素因子。我们知道，如果一个整数n不能够被小于等于的素数整除，那么它一定是一个素数。这一点对于小于n的整数自然也是成立的。换句话说,小于n的合数都能够被小于等于的某个素数整除，如果我们从n个数字中去除掉这些合数，那么剩下的都是素数了。假设小于等于的素数表示为,第一步，我们先从n个数中减去n和的倍数，即

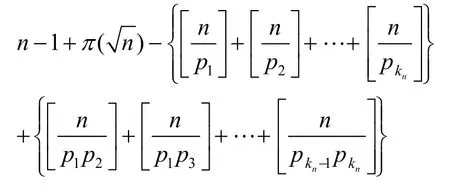
同样地，如果一个小于等于n的整数是三个素因子的乘积，那么这些数字在第一步运算中被减去了次,而在第二步运算中被加了次，由于，从而应当再减去一次，则有第三步的运算

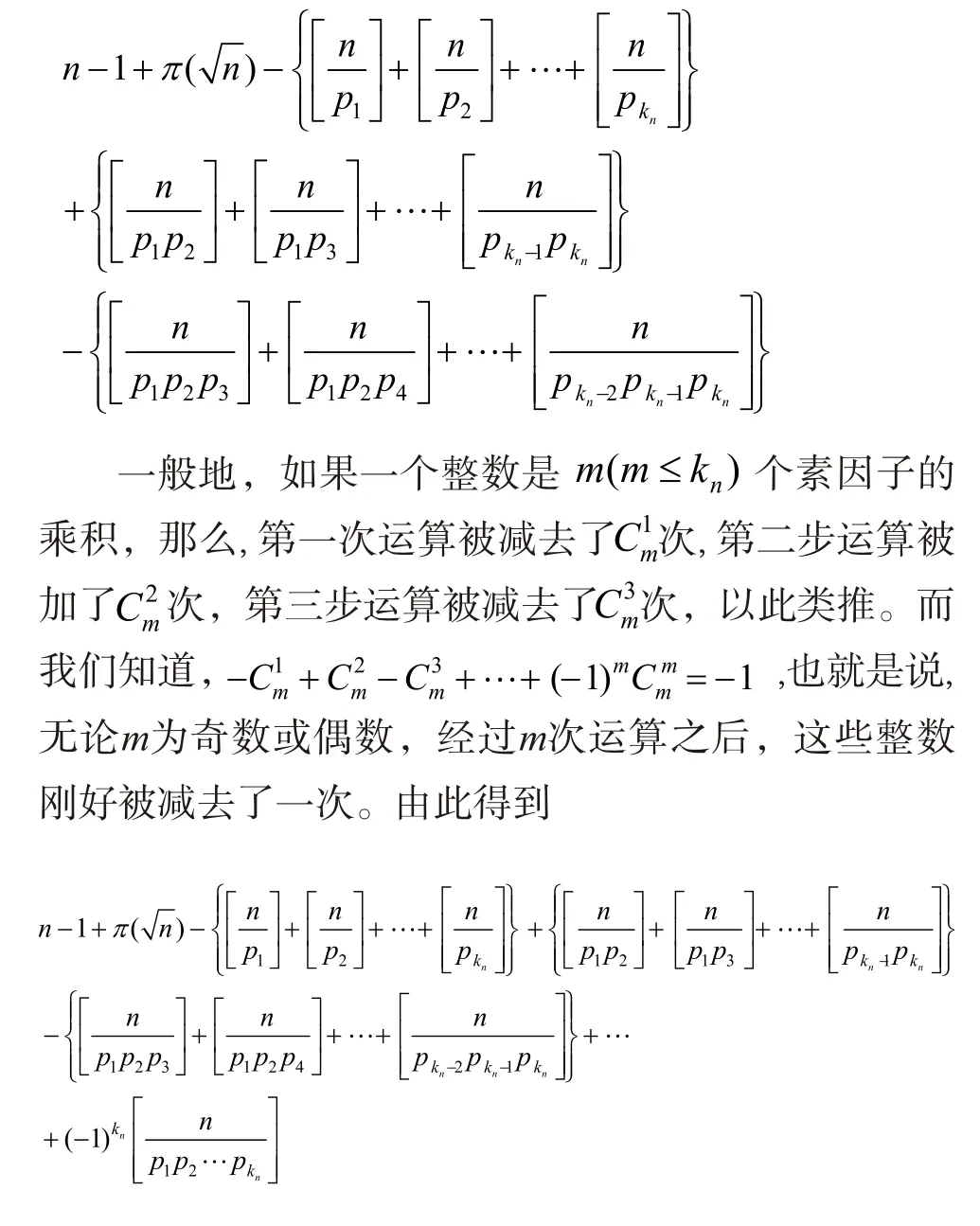
这样看起来似乎有些草率，但是，如果带着取整的符号来要求精确性，则公式就不能够得到简化。去掉取整的符号后，容易看到，(3)式就是连乘积的展开式，即

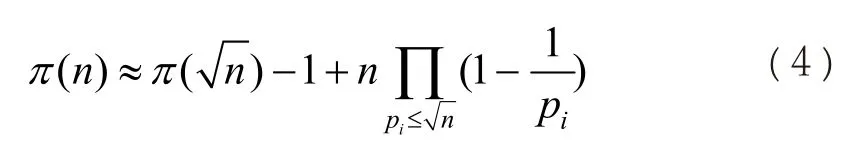
其二，(3)式当中可能会出现某些素因子的乘积大于n的情况，这些项其实是不存在的。但是，对于不同的n，我们又无法确定哪些素因子的乘积会大于n，这是(3)式无法弥补的缺憾。

例1 求小于100的素数个数。

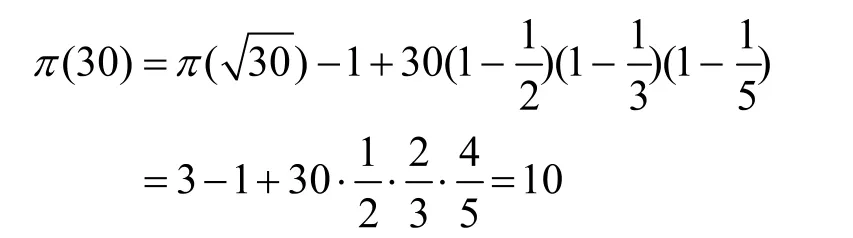
2.数值比较

表1 近似公式和素数真值 的数据比较

表1 近似公式和素数真值 的数据比较

3.结语

本文所述的方法只能说是对于素数分布进行的一种积极有益的探索。在大尺度上，(4)式有着无法弥补的缺憾。素数定理至今仍然是描述素数分布的最简单和足够精确的公式，这似乎意味着我们只能从统计的角度去对待素数。要获得比素数定理更为精确的结果，就必然需要面临更加复杂的公式，引入性态不太良好的函数和更加繁琐的计算。