这样教岂不是更好

朱小平

数学教学离不开习题。习题教学必须明方向、理思路、有逻辑、重思维，方能使学生摆脱思维之困，提升解题能力，发展学科素养。

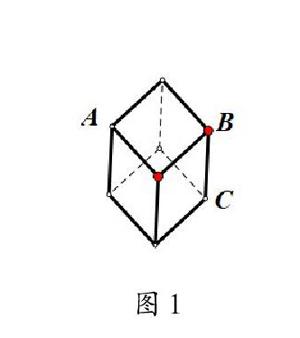
人教版数学七年级上册第130页习题4.2第11题是一道拓展探索题。如图1所示，一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B，怎样爬行路线最短？如果要爬行到顶点C呢？说出你的理由。

一次听课活动中，执教教师是这样处理的：学生以小组为单位边观察图1边讨论如何解题，用时20多分钟之后，教师让学生分享讨论结果，一共得到4种从点A到点C的最短路径。这样教学，不仅费时费力，而且效果不好。究其原因，教师在解决此题的过程中既没拿实物演示，也没有画出相应的展开图进行直观讲解，更没有深入地挖掘问题的本质，探索出行之有效的解决问题的方法。

接下来，笔者分享自己对于此题的探究过程。

首先，每个小组准备正方体盒子若干，按图2标注顶点A、B、C，并在六个面分别标注上、下、前、后、左、右字样。

然后，先后出示5个问题。

问题1：从点A到点B如何走最近？理由是什么？（两点之间，线段最短）

问题2：从点A到点C如何走最近？理由是什么？（从点A到点B再到点C）

问题3：上述答案对吗？对要说明理由，不对则给出正确路径并解释。

通过学生的解答，笔者发现，学生有转化问题的意识和实际拼接经验，但缺乏明晰的方向与有序的思考，只能借助直观、动手操作、观察发现获取从点A到点C的最短路径的部分方法，而不能将立体图形快速展开，准确形成点A、点C的共面，不重不漏地找出所有的最短路径。基于此，笔者继续出示了问题4。

问题4：刚才我们通过把盒子的某些面拆拼到一起，得到了一些最短路径，如果没有纸盒供拆拼，我们怎样才能迅速找到所有的最短路径呢？

通过小组合作交流，学生认为没有实物的情况下，只能借助图形思考，想象点A、点C拼在同一平面的情形。显然，学生只能从实践操作到空间想象，不能到达逻辑推理的高度，缺乏用数学的思维思考、分析、解决问题的能力。于是，笔者追问：研究一個几何对象，我们通常会从组成它的元素开始研究，那么正方体有哪些元素？（顶点、棱、面）从元素出发，这个问题又该怎样研究呢？学生发现，从点A到点C的最短路径必然与起点A和终点C这两个顶点元素有关，蚂蚁要从起点A沿正方体的表面爬行到终点C，一定会经过含点A和点C的面，而点A、点C不共面，点A在“前”“上”“左”三面，点C在“后”“下”“右”三面，寻求从点A到点C的最短路径，就是要将空间问题平面化，把含点A的面与含点C的面组合在同一平面（如图3），即利用“两点之间，线段最短”获取路径。

最后，为了更清楚、更有条理地表示这一过程，笔者用图4、图5、图6依序说明：前后、上下、左右这些两两相对的面可看成是对称的，若从前下、前右、上右组合的面可以找到最短路径，则其对称的组合上后、左后、左下也必然成立，只有相邻面才能拼接，而相对面平行，无法拼接。

通过对问题4的探讨，学生得出了找“直线爬行路径”的一般方法。那么，这些路径是否都是最短路径呢？笔者出示问题5：将立体图形展开成平面图形后，一共有6种从点A到点C的直线爬行路径，这些路径的长度一样吗？都是最短的吗？

学生通过比较路径长度，发现它们都是由两个相同大小的正方形组成的长方形的对角线的长度，故最短路径有6种，分别经过前下、前右、上后、上右、左后、左下这些面的展开图。

此题解决的是“空间内两点间的最短距离”问题，学生受思维定式影响，给出了从点A到点B再到点C的错误的直觉判断。此时，笔者让学生借助实物操作，将立体图形转化为平面图形，探索发现了正确结论。笔者引导学生从直观走向抽象、从想象走向推理，由一道题的讨论引申出一般思想方法的运用。

（作者单位：襄阳市襄州区教育教学研究中心）

责任编辑  张敏