基于边缘保持滤波和改进核模糊聚类的脑肿瘤图像分割方法*

王志刚, 冯云超

(湖南师范大学 信息科学与工程学院 ,湖南 长沙 410081)

0 引言

根据世界卫生组织的最新统计，脑肿瘤是世界上最常见的癌症死亡类型之一[1]，且脑肿瘤的发病率和死亡率近年呈上升趋势，对人类的生命健康造成了严重的威胁.在疾病诊断过程中，准确获得脑肿瘤的尺寸、形状等信息能够为脑疾病的治疗提供很大的帮助.因此，将脑部肿瘤从核磁共振成像(Magnetic Resonance Images,MRI)图像中准确完整地分割出来对于脑疾病的诊断具有重要的意义.

MRI对人体无电离辐射伤害，有较高的安全性[2]，并且对人体软组织显示清晰，因此被广泛地应用于脑部疾病的诊断和治疗中[3].然而，由于人类的脑部结构非常复杂，且MRI成像存在边缘模糊、灰度不均匀、易受噪声干扰等问题[4]，因此脑肿瘤MRI图像分割一直是研究的热点和难点问题.

核模糊C-均值聚类算法(KFCM)是一种无监督聚类算法，具有效果稳定、运算速度快等特点，因此被广泛地应用于医学图像处理领域[5].然而，KFCM算法对于噪声较为敏感，且聚类精度不高，降低了算法的实用性.为此，学者们对该算法进行了大量的研究和改进，王燕等[6]将核模糊聚类算法与马氏距离相结合，提出一种FCM-KM算法，抗噪性得到明显提升；汪敏等[7]将核函数与模糊局部信息聚类相结合，提出了一种基于方差系数加权的模糊聚类分割方法，具有较好的抗噪性和分割精度；Hua L等[8]将PSO算法与KFCM算法相结合，进一步提高了算法的分割准确率.但是，这些优化算法大多数只考虑了像素的灰度信息，忽略了像素之间的邻域信息，并且采用单个高斯核函数进行数据映射，限制了算法的泛化和学习能力，因此仍然存在一些过分割和欠分割现象，并且对于噪声的鲁棒性也不高.

针对现有算法的不足，本文提出一种基于边缘保持滤波和改进核模糊聚类的脑肿瘤图像分割方法.实验表明，该方法在去除噪声的同时保留了更多的图像边缘信息，具有较好的噪声鲁棒性，并且分割精度也更高.

1 加权引导滤波

传统的去噪算法虽然能有效去除图像中的噪声，但是却模糊了图像的边缘，不利于医学图像的后处理，本文采用一种新型的加权引导滤波算法进行图像预处理，在去除噪声的同时可以把图像的边缘较好地保留下来.

1.1 引导滤波

引导滤波是何凯明等[9]提出的一种新型滤波器，它假设输入与输出之间存在如下的线性关系：

qi=akIi+bk,∀i∈wk，

(1)

其中：q为输出图像；I为引导图像；i和k为像素索引；a、b是当窗口w中心位于k时该线性函数的不变系数.为了使输入图像p与输出图像q的差别最小,使其转化为最优化问题,其代价函数为：

(2)

其中：ε为调整系数，是为了防止ak过大；p为输入图像；I可为任意图像，也可以是输入图像本身.利用线性回归，可解得系数a、b：

(3)

(4)

1.2 加权引导滤波

由于原始的引导滤波算法，在不同的窗口内采用了相同的ε调整系数，没有考虑到不同窗口内像素之间的差异性，使得边缘保持效果不佳.Li等[10]提出一种基于方差的加权引导滤波算法，它使用3×3窗口内的局部方差计算边缘权重,利用边缘权重对调整系数ε进行惩罚，来增强算法的鲁棒性，其定义如下：

(5)

由于并不是所有方差较大的区域都对应图像的边缘区域，所以使用局部方差计算的边缘权重并不是很好的边缘惩罚因子.本文采用基于Canny算子的边缘权重代替文献[10]中的局部方差，Canny算子在边缘监测中精确度较高，但是传统的Canny算子为了避免噪声的影响会先进行高斯滤波去噪操作，由于高斯滤波不能很好地保护图像的边缘，所以本文采用基于双边滤波的Canny算子，在降噪的同时还能很好地保留边缘信息.改进后的权重因子定义如下：

(6)

其中：CB(i)为双边滤波Canny算子；γ取(0.001×L)2，L为图像的灰度值范围；N为像素总数.这样一来，图像的边缘部分就会比平坦部分分配到更大的权重，将边缘权重因子引入到代价函数中可得：

(7)

利用线性回归，求解系数a、b得：

(8)

(9)

2 改进的核模糊聚类算法

2.1 混合核函数模糊聚类算法

核模糊聚类算法的基本思想是将原始数据通过核函数映射到高维特征空间进行处理[11]，这样可以突出不同类别样本之间的特征差异，使得其在高维特征空间中变得线性可分，然后再进行模糊C均值聚类得到分割结果.

设X={x1,x2,x3,…,xn}是原始空间Rs通过非线性变换φ(·)映射至特征空间Rp上的一个数据集，则KFCM算法在高维特征空间下的目标函数为：

(10)

传统的核模糊聚类算法(KFCM)采用单一的高斯核函数进行数据映射，其定义为：

(11)

由于单一高斯核函数仅有一个可以调节的参数σ，这对聚类算法的学习和泛化能力起到了一定的限制作用[12]，所以本文采用混合高斯核函数来替代原先的单一高斯核函数，这样可以通过调整多个σ参数来优化数据在高维特征空间中的分布，可以有效提高算法的性能.

混合高斯核函数的定义如下：

(12)

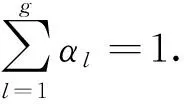
2.2 基于MRF和混合核函数的模糊聚类算法

为防止滤波后的残余噪点对图像分割造成干扰，本文将马尔科夫随机场的局部先验概率引入到算法中，由于其考虑了像素的邻域信息，因此具有较强的抗噪性.

假设yij是(i,j)像素点的灰度值，yij=k表示该像素点属于第k类，设该像素点的马尔科夫模型为y={yij|yij∈K}，其中K={1,2,3,…,k}，k为类别数，根据Hammersley-Clifford定理，吉布斯随机场与马尔科夫随机场是等效的[13]，可以得到马尔科夫随机场的先验概率计算公式：

(13)

其中：Ω表示标号场；y为标号场中的元素；U(y)代表能量函数，其定义如下式：

(14)

其中：c表示基团；C表示基团集合；Vc(y)表示势团函数，其定义如下式所示：

(15)

其中：yt为邻域像素的标号；ys为中心像素标号；β为势团参数.

本文在混合核函数聚类算法的目标函数中添加一正则项，将马尔科夫随机场的先验概率引入，增强算法的抗噪性，改进的目标函数如下式所示：

(16)

其中:uij为第j个数据对第i类的隶属度；dij为第j个像素到第i个聚类中心在核空间中的欧式距离；Pij表示马尔科夫随机场的先验概率；λ为约束系数.

根据拉格朗日乘数法，可以求得隶属度迭代公式如式(17) 所示，聚类中心迭代公式如式(18)所示：

(17)

(18)

3 算法的实现过程

3.1 粒子群算法确定聚类中心

由于核模糊聚类算法的初始聚类中心为随机确定，容易陷入局部极值造成算法的不稳定性，所以对上述算法做出进一步改进，利用粒子群算法初始化聚类中心，增强算法的稳定性.

粒子群优化 (Particle Swarm Optimization，PSO) 算法是由Kennedy和Eber-hart提出的优化算法[14].该算法是受到鸟群搜寻食物飞行行为启发提出的，具有易实现、需调节参数少、收敛速度快等优点.

在D维搜索空间中由N个粒子汇聚成一个群落，群落中的每个粒子都在寻找自己的最佳位置，第i个粒子由Xi=(xi1,xi2,…,xiD)表示位置，由Vi=(vi1,vi2,…,viD)表示其速度，搜寻过程中，个体的最优位置定义为pi=(pi1,pi2,…,piD)，记为pbest，群体中所有粒子在之前搜寻过程中的最佳位置用g表示，记为gbest.粒子的速度和位置更新公式如下所示：

(19)

(20)

其中：c1和c2为学习因子；r1和r2是两个随机值，取值范围为[0,1]；w是惯性权重.

3.2 算法的具体步骤

算法的具体实现过程如下：

步骤1：设定加权引导滤波算法的相关参数，规整化因子为0.01，半径为3，对图像进行去噪预处理；

步骤2：设定粒子群算法的相关参数，粒子群规模N=30，最大迭代次数tmax=30，学习因子c1=c2=2，然后通过粒子群算法求得算法的初始聚类中心V(0)；

步骤3：设定聚类数目c=3，迭代终止条件ε=10-5，最大迭代次数Tm=100，高斯核数目g=2，高斯核参数σ1=150，σ2=20，核函数权重因子α1=0.7，α2=0.3，正则项约束系数λ=0.6；

步骤4：输入由步骤2获得的初始聚类中心V(0)，根据式(17)和式(18)不断更新聚类中心Vi和隶属度矩阵U，如果‖J(i)-J(i-1)‖≤ε或者达到最大迭代次数，则停止迭代，否则继续进行本步骤；

步骤5：根据最终得到的隶属度矩阵把目标像素指定为相应的最佳聚类中心的值，输出图像；

步骤6：结合形态学对图像进行后处理，平滑肿瘤图像的边缘.

4 实验结果及分析

4.1 实验环境

本次实验的脑肿瘤MRI图像来自BraTS2018数据库，该数据库的MRI图像共有四种形态，分别是 T1、T1c、T2 和 FLAIR，由于FLAIR图像常用于发现肿瘤[15]，所以本次实验选择FLAIR图像.实验环境为Windows10、AMD Ryzen5 3500U处理器和16 GB内存，实验平台为Matlab 2018a.

4.2 加权引导滤波算法去噪实验

为了证明加权引导滤波算法的有效性，从数据库中随机挑选某位患者的脑肿瘤MRI图像，抽取其第65张切片和第75张切片为实验图像，在图像中添加方差为0.01的高斯噪声，使用该算法进行去噪，并且同原始引导滤波[9]、双边滤波[16]和基于方差的加权引导滤波[10]进行对比，算法的相关参数均采用原文献中的推荐参数，其去噪效果如图1～图3所示.

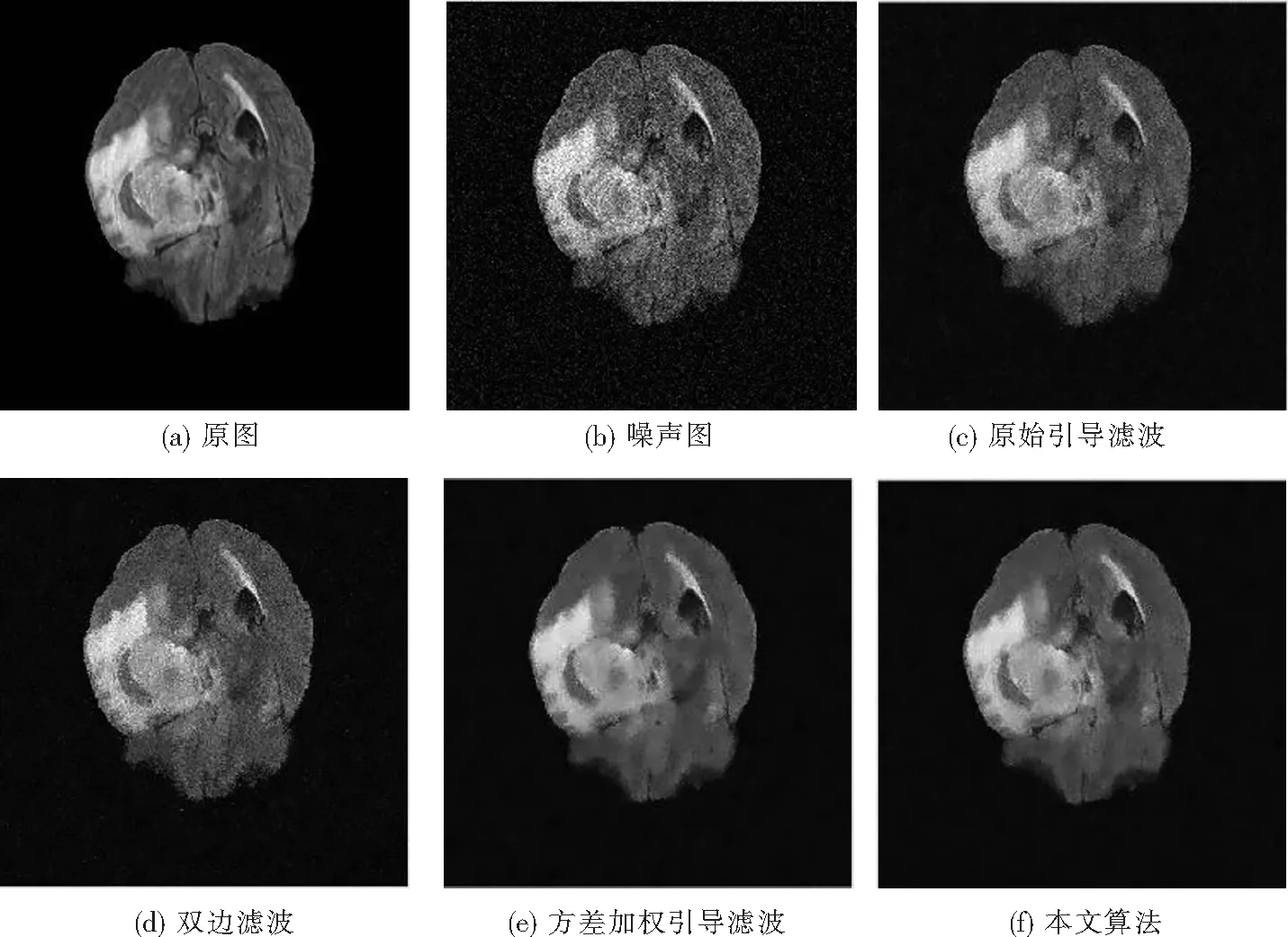
图1 第65张切片的去噪效果Fig.1 Denoising effect of the 65th slice

从图1和图2可以看出，本文算法在视觉效果上强于其他保边滤波算法，去噪后的图像无明显噪点；从图3和图4可以看出，经本文算法去噪后，图像边缘清晰，跟原图像最接近，其他算法的涂抹感较为严重.为了防止主观评价因素的影响，本文选择峰值信噪比(PSNR)和结构相似性(SSIM)两个评价指标对算法进行评估，两者的值越大说明算法降噪性能越好.

图2 第75张切片去噪效果Fig.2 Denoising effect of the 75th slice

图3 切片65细节放大图Fig.3 Enlargement of section 65 details

图4 切片75细节放大图Fig.4 Enlargement of section 75 details

峰值信噪比定义如下：

(21)

其中：MAX表示图像的灰度级；MSE表示原图像与处理图像之间均方误差.

结构相似性定义如下：

(22)

以上面两幅图像为例，对四种算法的PSNR值和SSIM值进行比较，比较结果如表1所示.

表1 不同降噪算法的比较

从表1可以看出，改进算法的PSNR值和SSIM值均高于传统算法，两幅图片的PSNR平均值相比传统算法提升0.804 1～2.096 2 dB，SSIM平均值相比传统算法提升0.031 2～0.065 4，说明改进算法的性能更好，适用性更强，能有效去除脑核磁共振图像中的高斯噪声.

4.3 脑肿瘤分割实验

为了证明所提算法对于脑肿瘤分割的有效性，从数据库中随机挑选某位患者的脑肿瘤MRI图像，抽选3个切片，并且向图像中添加方差为0.01的高斯噪声来模拟噪声环境，经改进加权引导滤波算法去噪后，分别使用FCM算法[17]、KFCM算法[18]、FLICM算法[19]和本文算法进行图像分割，分割结果如图5～图7所示.

图5 切片1分割结果对比Fig.5 Comparison of segmentation results in section 1

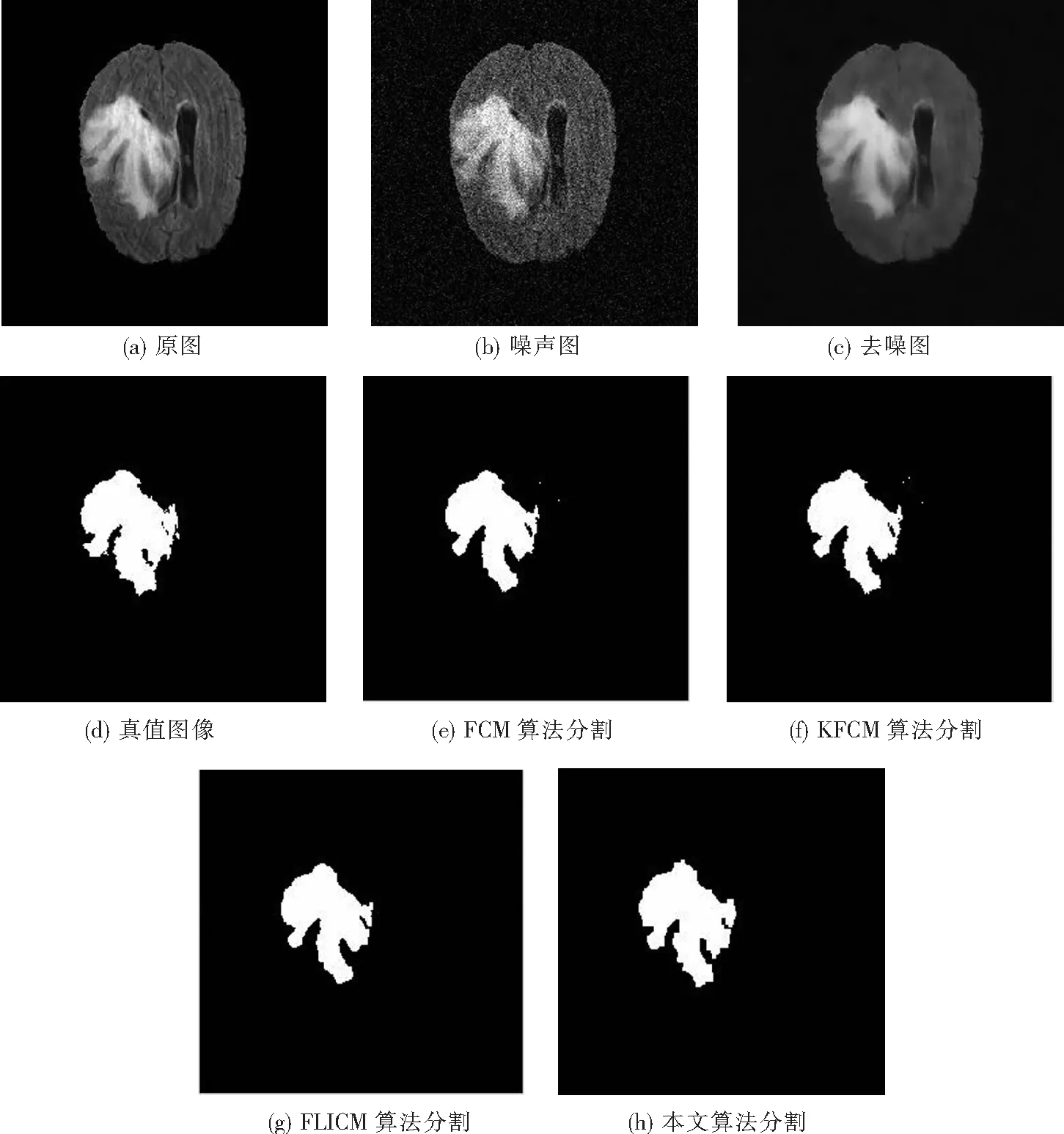
图6 切片2分割结果对比Fig.6 Comparison of segmentation results in section 2

图7 切片3分割结果对比Fig.7 Comparison of segmentation results in section 3

从图5、图6和图7可以看出，本文算法能够较好地处理脑肿瘤的边缘部分，且分割精度更高，分割效果最接近于真值图像.为了避免主观评价因素的影响，本文选择 Dice系数、Jaccard系数、Sensitivity系数、Accuracy系数四个评价指标对算法进行评估，其定义分别如下：

(23)

(24)

(25)

(26)

其中：TP为正确分割的目标区域；FP为误分割的目标区域；FN为没有检测到的目标区域；TN为一定的非目标区域.

仍然以上述三幅脑肿瘤MRI图像为例，将本文算法同FCM算法、KFCM算法和FLICM算法进行比较，比较结果如表2所示.

表2 本文算法与其他算法的分割性能对比

由表2可以看出，本文算法在四个指标上均有较高的数值，相较传统聚类算法有一定提升，Dice平均值高出传统算法1.69%～2.45%，Jaccard平均值高出传统算法3.03%～4.35%，Sensitivity平均值高出传统算法4.65%～5.87%，Accuracy平均值高出传统算法0.16%～0.23%.在肿瘤分割实验中，通常以Dice和Jaccard作为主要评价指标，其值越接近1，代表分割结果越精确.在本次实验中，本文算法的Dice平均值达到0.955 1，Jaccard平均值达到0.914 1.

5 结语

本文提出的脑肿瘤图像分割方法，利用改进的加权引导滤波算法进行图像预处理，具有良好的保边抗噪性；同时，通过粒子群算法确定初始聚类中心，提高了算法的稳定性；并且利用多个高斯核函数进行数据映射，可以优化算法的分割性能，最后通过马尔科夫随机场先验概率对算法的目标函数进行修正，进一步增强了算法的抗噪性.实验结果表明，所提方法能在有效去噪的同时，较大程度上保留图像的边缘信息，与FCM算法、KFCM算法和FLICM算法相比，分割精度更高，能将脑肿瘤从脑MRI图像中准确地分割出来，是一种有效的脑肿瘤图像分割算法.但是，在高斯核的参数调节上，需要一定的先验知识，限制了算法的灵活性，实现高斯核参数的自动调节，将是下一步研究的重点.