多场耦合作用下天然土质边坡安全性数值仿真研究*
2021-09-30谢承煜刘承波朱佳妮钟红军谢洪高盛美玉
谢承煜, 刘承波, 朱佳妮, 钟红军, 谢洪高, 盛美玉
(湘潭大学 环境与资源学院,湖南 湘潭 411105)
0 引言
随着经济高速发展,各项基础建设蓬勃兴起,如水利水电、房屋建设、能源与交通以及矿山开采等,都不可避免地遇到各类边坡安全问题.在工程实际中,边坡往往承受多物理场耦合作用,边坡体的存在状态更是一个复杂的体系,包括压力(如重力、边坡开挖后的应力重新分布以及地震活动引起的动态载荷)、水力(如地下水流渗入和雨水入渗)和边坡体本身力学结构等,在多种影响因素的耦合下,导致了边坡体的失稳破坏[1-4],其所造成的人员和财产损失备受社会关注,其中,以天然土质结构为主的边坡相较于岩质边坡而言更易于发生失稳破坏,主要的灾害类型为滑坡灾害,是工程建设中的重点防治对象,且我国又是一个滑坡等自然灾害频发的国家[5-8],根据国家统计局地质灾害数据显示(如图1),以2019年为例,全年地质灾害共发生6 181次,其中滑坡灾害占4 220次,累计占全年灾害次数的68.3%,是崩塌灾害的3倍.
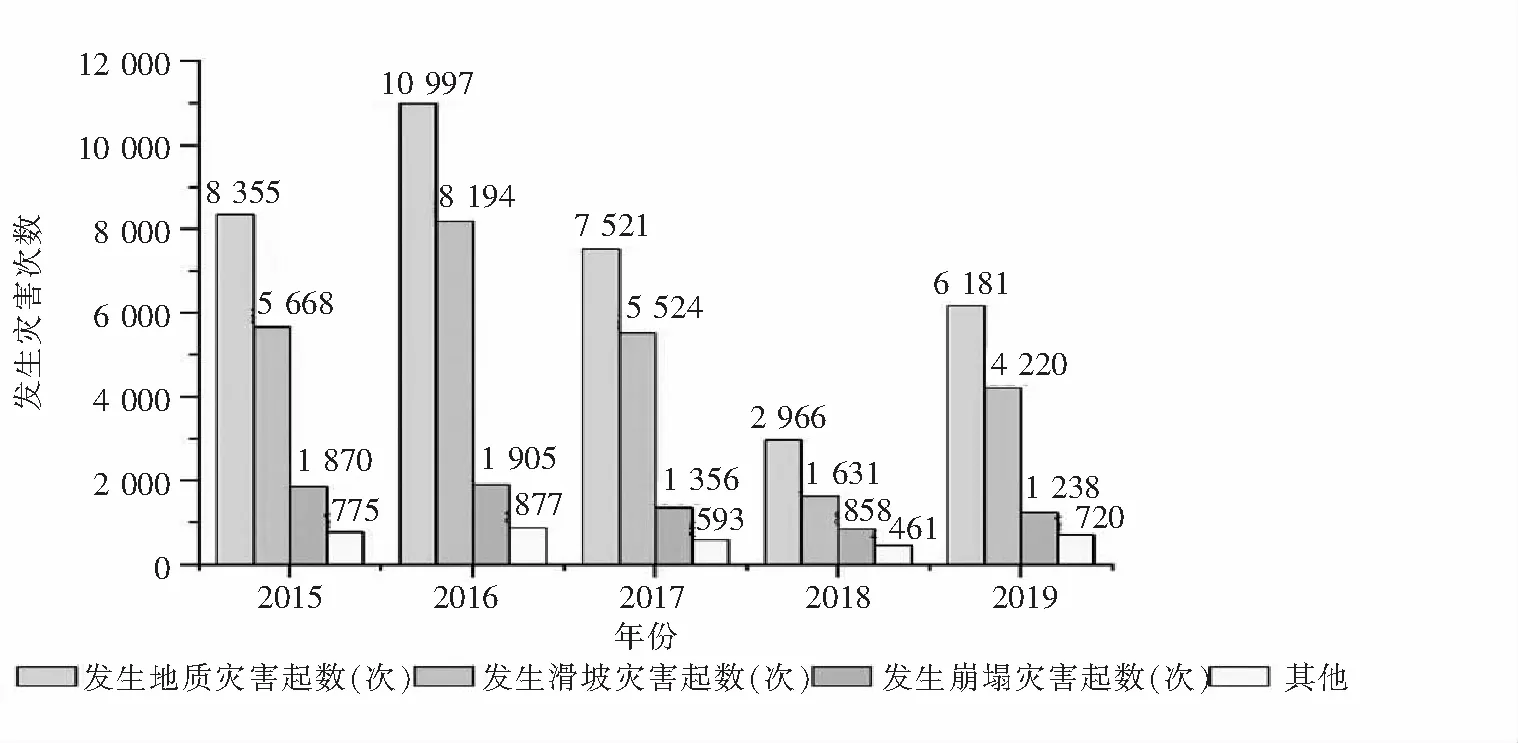
图1 我国近五年地质灾害数据柱形图Fig.1 Column chart of geological hazard data in recent five years in China
物理场耦合作用于边坡体的稳定性分析经过了较长的发展历程,由两场耦合到三场耦合再到四场耦合的研究,随着数学理论方法的不断发展,科学技术的不断进步,对边坡多场耦合作用的数学模型建立及数值模拟计算方式也得到了不同程度的改善.蔡亚飞等[9]运用ABAQUS对渗流-应力耦合及降雨入渗作用下的边坡进行了稳定性分析;张良以等[10]结合数值模拟运用对渗流场-应力场-膨胀应变场耦合下非饱和膨胀土边坡逐渐破坏演化规律进行了系统的研究;朱和玲等[2]运用数值模拟方法研究了基于降雨-地震耦合作用的土质边坡稳定性;Wu等[11]对温度场-渗流场-机械荷载耦合下的边坡变化特性进行了数值模拟,并与传统的极限平衡计算结果进行了对比;Qu等[12]运用COMSOL Multiphysics 对应力场-渗流场-温度场-化学场耦合下的岩质边坡进行了稳定性研究.尽管对多场耦合作用于边坡体的稳定状况已取得了一些研究成果,但仍不够完善,作用于边坡体的多种物理场之间的相互作用、相互影响是一种非常复杂的关系,不同的研究手段、内外在因素的不同等都会造成研究结果的差异,故仍需加以改进或完善,使其更贴近于实际应用.基于此,本文对在多场耦合作用下边坡的安全性展开研究,利用数值模拟分析方法,揭示天然土质边坡在降雨-渗流-应力场耦合作用下的位移变形规律,以期达到边坡安全防护的目的.
1 多场耦合作用下土质边坡安全性数值模拟
运用COMSOL Multiphysics软件进行数值模拟计算,通过建立二维有限元模型,设置降雨-渗流-应力耦合工况参数,并分阶段进行求解,从应力、塑性、位移等云图中提取数据,以此分析土质边坡的变化特性.
1.1 建立几何有限元模型
(1) 几何模型
为方便操作,导入在CAD软件中构建的二维边坡模型,如图2所示,其边界范围:左右边界距离取54 m,上下边界距离取30 m,坡面顶点距左边界的距离取20 m,坡角距右边界的距离取10 m、距下边界的距离取10 m.同时,为了不影响边界设定和求解域的完整性,对CAD导入模型作修复操作,相对修复容差为1.0×10-5[13].
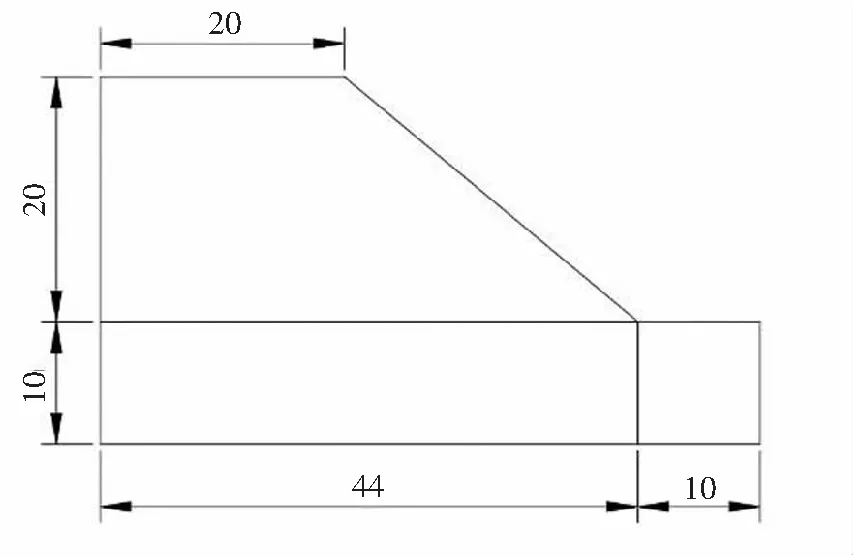
图2 二维土质边坡模型尺寸图(单位:m)Fig.2 2D dimension drawing of soil slope model(unit:m)
(2) 网格剖分
为了更为精确高效地对几何模型进行网格剖分,将网格的序列类型切换为用户控制网格,网格剖分方式为映射,共剖分1 699个单元(如图3所示).其中,在映射设置中的“域选择”依次点击几何模型的域,直至选中整个模型,且在尺寸设置中,将“预定义”设置为超细化,单元大小参数:最大单元大小为1.08 m,最小单元大小为0.004 03 m,最大单元增长率为1.2,曲率因子为0.25,狭窄区域分辨率为1[14].

图3 二维土质边坡网格剖分图Fig.3 2D mesh subdivision of soil slope
(3) 材料参数
材料参数的设定决定了材料的变化特性,边坡土体的材料为弹塑性材料,服从Drucker-Prager准则和莫尔-库伦准则[15-16],其参数如表1所示.

表1 二维土质边坡土体的材料参数表
(4)边界条件
边坡模型的下边界设置为固定约束,左右边界为辊支承,则其余为自由边界;同样,在“体积力”的扩展选项中选择重力,且在重力设置中选择所有域,为边坡模型添加自重力.
1.2 工况分析设计方案
土质边坡在受物理场作用的情况下,其应力及孔压随时间在不断变化,为确保土质边坡的变形在物理场作用下产生,而非自重力,故分四步层层递进(如图4所示),将物理场接口分为四组(如表2所示);先计算土质边坡在弹性状态下的初始应力和孔压,进而将所得结果导入后计算土质边坡在塑性状态下的应力和孔压,此时土质边坡在降雨渗流条件下为动态变化,即为瞬态研究,最后求算出土质边坡在强度折减法下的位移变形和塑性应变.
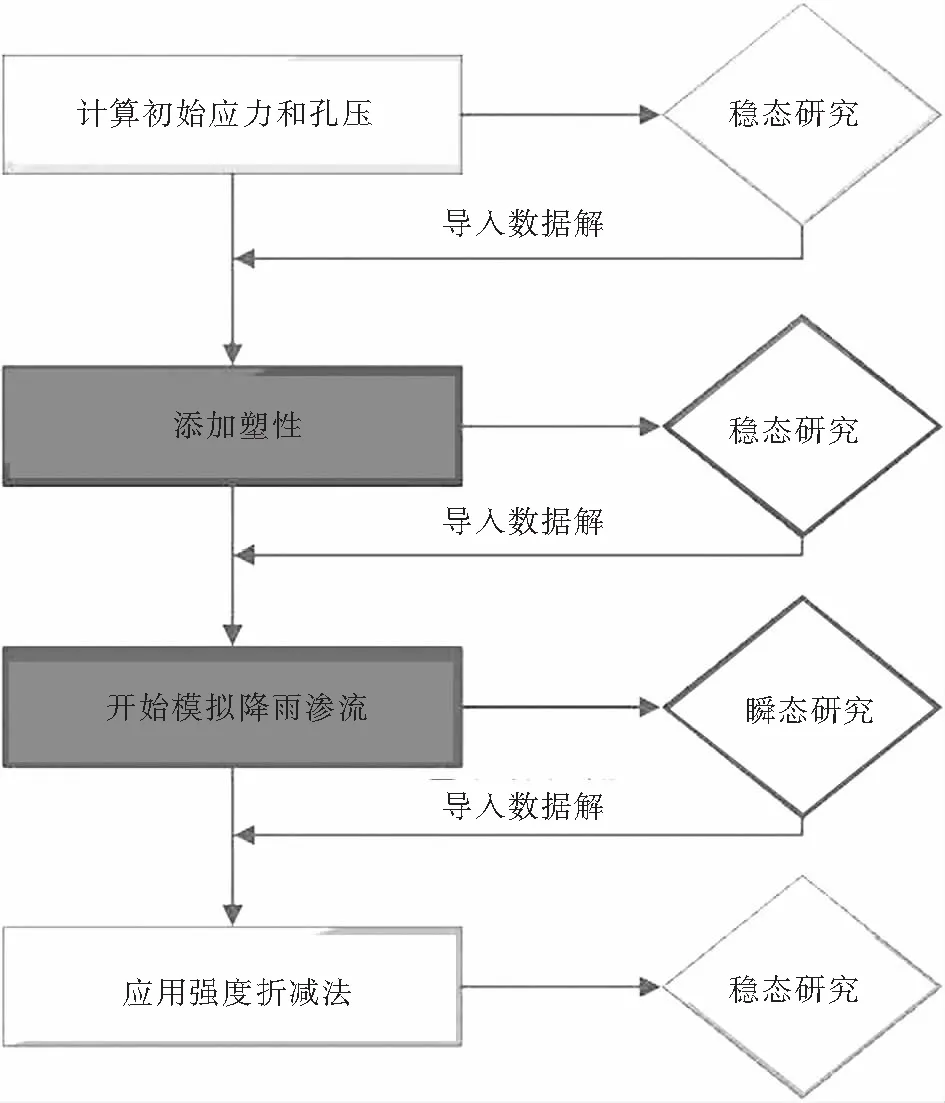
图4 工况分析步骤图Fig.4 Working condition analysis step diagram

表2 工况分析设计方案表

表2(续)
2 计算结果分析
为每一个研究步骤选择好物理场接口后,通过求解得到各个研究步骤的计算结果.
2.1 初始应力与孔压
为了确保土质边坡的变形是受物理场作用下所产生的,而非自重力,在进行多场耦合计算之前,需要先对土质边坡进行初始应力与孔压的计算,如图5和图6所示.
从图5中可以得出初始主应力分布整体呈波浪形,由边坡内部向外辐射,层状边界清晰,可明显得出边坡主应力分布走向,层次感较强,并在坡顶和坡脚处出现了剪应力集中现象;从图6中可以得出边坡受自重影响,其压力主要集中在边坡底部,分布均匀,层状清晰,并在边坡底部出现压力最大值,压力值随高度的增大而减小.
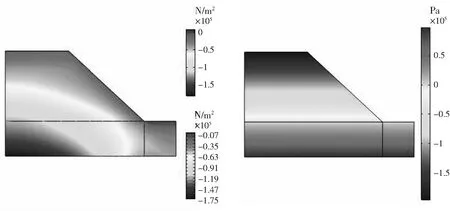
图5 初始主应力等值云图 图6 压力云图Fig.5 Contour map of initial principal stress Fig.6 Pressure nephogram
2.2 添加塑性变化
将第一组物理接口的解导入第二组物理接口中,并为模型添加塑性变化,则得到如图7~10结果.
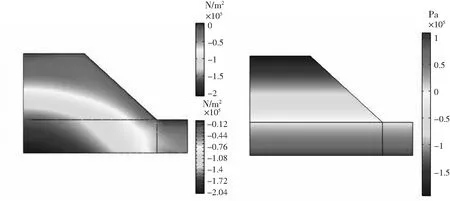
图7 弹塑性状态下主应力等值云图 图8 弹塑性状态下压力云图Fig.7 Isogram of stress in elastoplastic state Fig.8 Pressure nephogram in elastoplastic state
从图7~图10可以得出,将研究1的结果导入第二组物理接口,并为边坡土体材料添加土壤塑性,边坡土体材料由原来的弹性添加塑性变化为弹塑性本构模型后,对比图5和图7,其应力集中表现在弹塑性状态下相比较有缓和;对比图6和图8,其压力分布范围无明显变化,压力分布水平稍有点下移;土质边坡有效塑性应变如图9所示,主要集中在坡角处,呈椭球状;如图10所示,土质边坡在弹塑性状态下的最大位移主要表现在坡顶至下坡面,呈弧形状,并在距坡面不远处有集中体现.
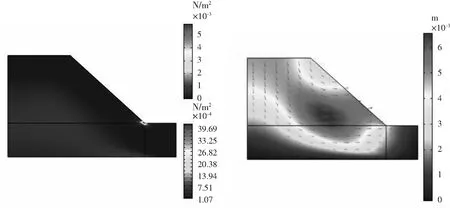
图9 弹塑性状态下有效塑性应变等值云图 图10 弹塑性状态下位移云图Fig.9 Equivalent nephogram of effective plastic strain in elastoplastic state Fig.10 Displacement diagram in elastoplastic state
2.3 降雨-渗流-应力场耦合
根据上一组物理接口得到的结果导入第三组物理接口中,并从应力、饱和度、塑性、位移四个方面选取具有显著特点的三个不同时间段的特征进行分析.
(1) 应力特征
图11中(a)为降雨渗流前主应力等值云图,(b)为降雨渗流12 h后主应力等值云图,(c)为降雨渗流120 h后主应力等值云图.土质边坡在降雨渗流后的主应力变化不明显,层次清晰,尤其在降雨渗流12 h后与之相比无明显变化,但从图中可以得出,在坡顶至坡角处有应力集中体现,尤其在坡角处应力集中明显,且有缓慢向边坡内部延伸现象.
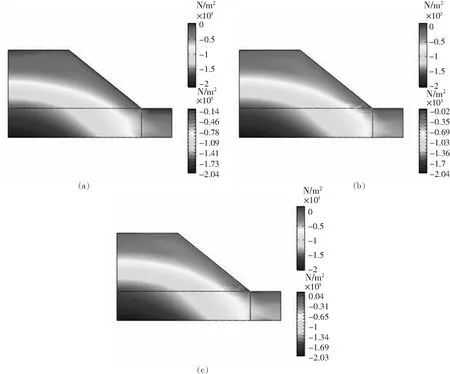
图11 主应力等值云图Fig.11 Principal stress contour map
(2) 饱和度特征
采用Richards方程模型,水力传导率为0.2 m/h,并在右边界和左下边界设置10 m的压力水头,压力水头与压力水头时间变化关系如图12所示:其随时间变化呈圆弧形下降.图13中(a)为降雨渗流前饱和度云图,(b)为降雨渗流72 h后饱和度云图,(c)为降雨渗流120 h后饱和度云图.随着时间的推移,由于降雨渗流作用,水流向边坡体内渗流,土壤由非饱和状态转变为局部饱和状态,或由非饱和到饱和渐变向内扩张.
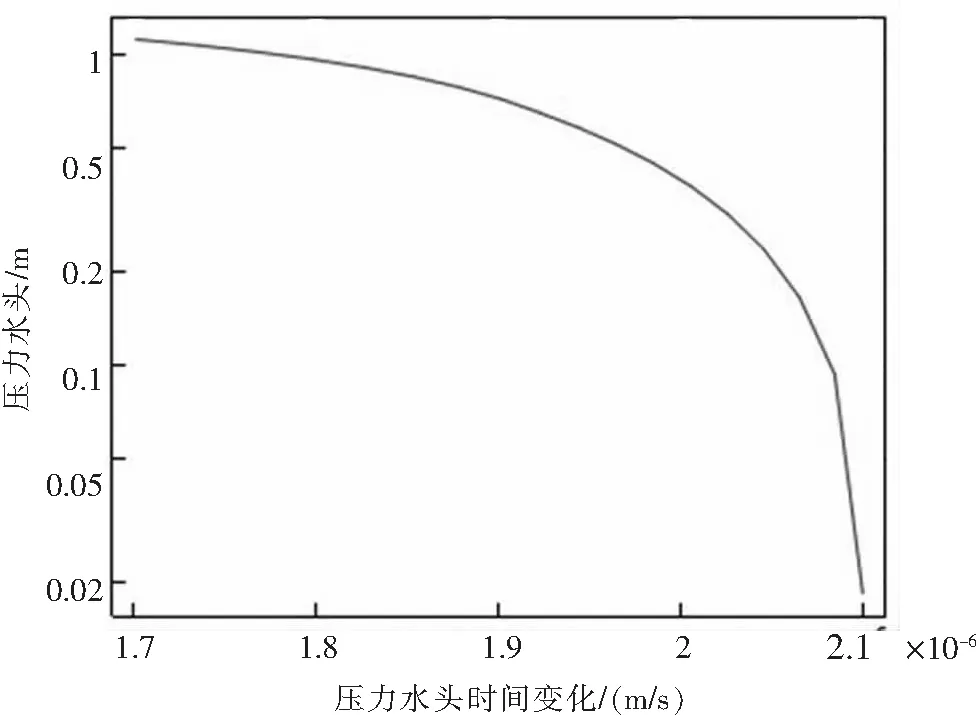
图12 压力水头与压力水头时间变化关系曲线图Fig.12 Pressure head and pressure head time variation curve
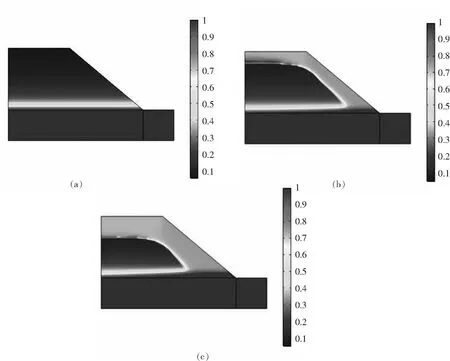
图13 饱和度云图Fig.13 Saturation nephogram
(3)塑性特征
图14中(a)为降雨渗流2.4 h后有效塑性应变云图,(b)为降雨渗流4.8 h后有效塑性应变云图,(c)为降雨渗流120 h后有效塑性应变云图.土质边坡有效塑性应变主要表现为由坡角处向边坡体内延伸,即坡角处为最先发展并开始出现的位置,且以较慢的速度向边坡内部扩大,呈弧形状,而后受到周围土体的约束,在降雨渗流4.8 h后无明显变化.
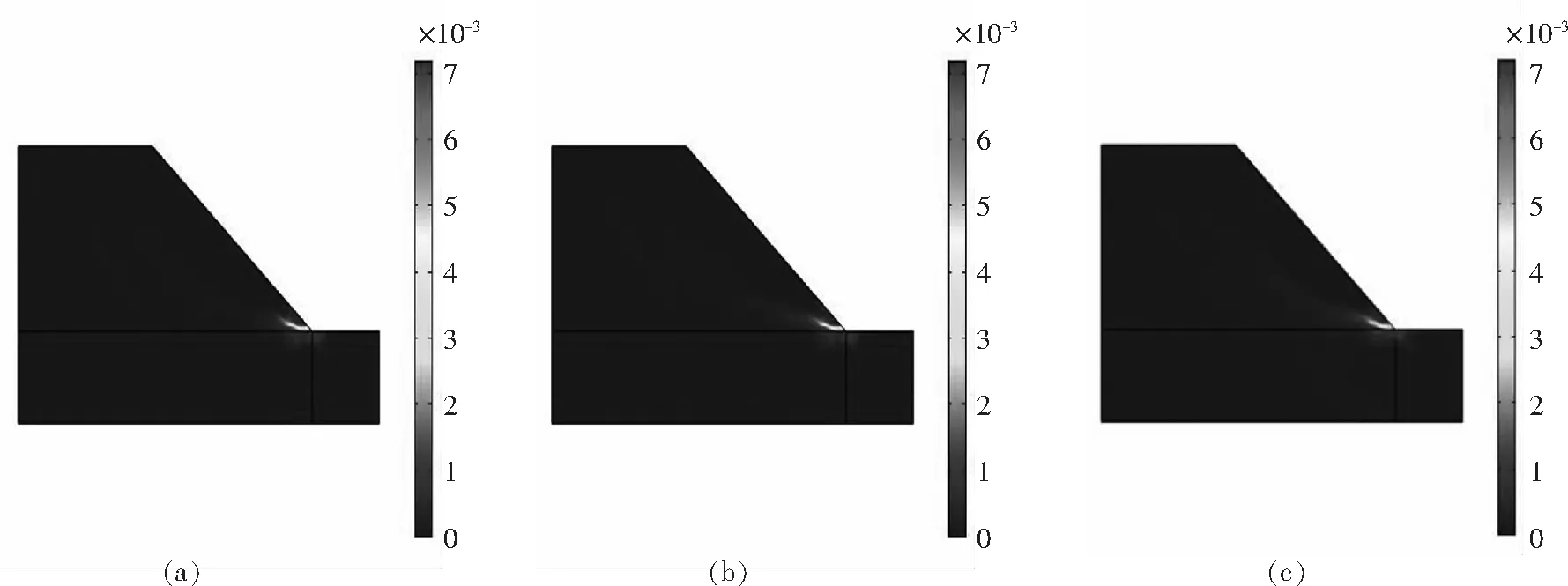
图14 有效塑性应变云图Fig.14 Effective plastic strain nephogram
(4)位移特征
由图15所示,其中:(a)为降雨渗流24 h后位移云图,(b)为降雨渗流72 h后位移云图,(c)降雨渗流120 h后位移云图.土质边坡在降雨-渗流-应力场耦合作用下的位移表现为由边坡内部向坡表面逐渐增大,并出现了由上坡面至坡角聚集的现象,在坡角处的位移最大,且最为明显.针对降雨渗流后的边坡位移数值进行提取,以坡肩位移和坡角位移为例,并绘制曲线图,如图16所示.

图15 位移云图Fig.15 Displacement nephogram

图16 坡肩和坡角位移曲线图Fig.16 Displacement curve of slope shoulder and slope angle
由图16可知,坡肩与坡角的位移变化可分为两个阶段,即以降雨渗流1.4 h为分界点,在降雨渗流1.4 h前呈直线上升,降雨渗流1.4 h后,坡角位移曲线呈弧线上升,而坡肩的位移曲线上下浮动较大,呈波形状.
2.4 结合有限元强度折减法应用
有限元强度折减法是边坡稳定性有限元分析领域的常用方法,其实质就是通过对模型进行单元划分,将其划分为微小单元,从而达到更为精确的计算,进而对材料的黏聚力和内摩擦角折减并不断带入模型迭代计算,直至不收敛则表示模型已经达到极限,发生土体失稳[17];此方法能够很好地解决有限元模拟复杂的问题,结果更为直观,在工程中有着广泛的应用,下面将对土质边坡在降雨-渗流-应力场耦合作用下的位移及塑性变化结果进行分析,如图17所示.
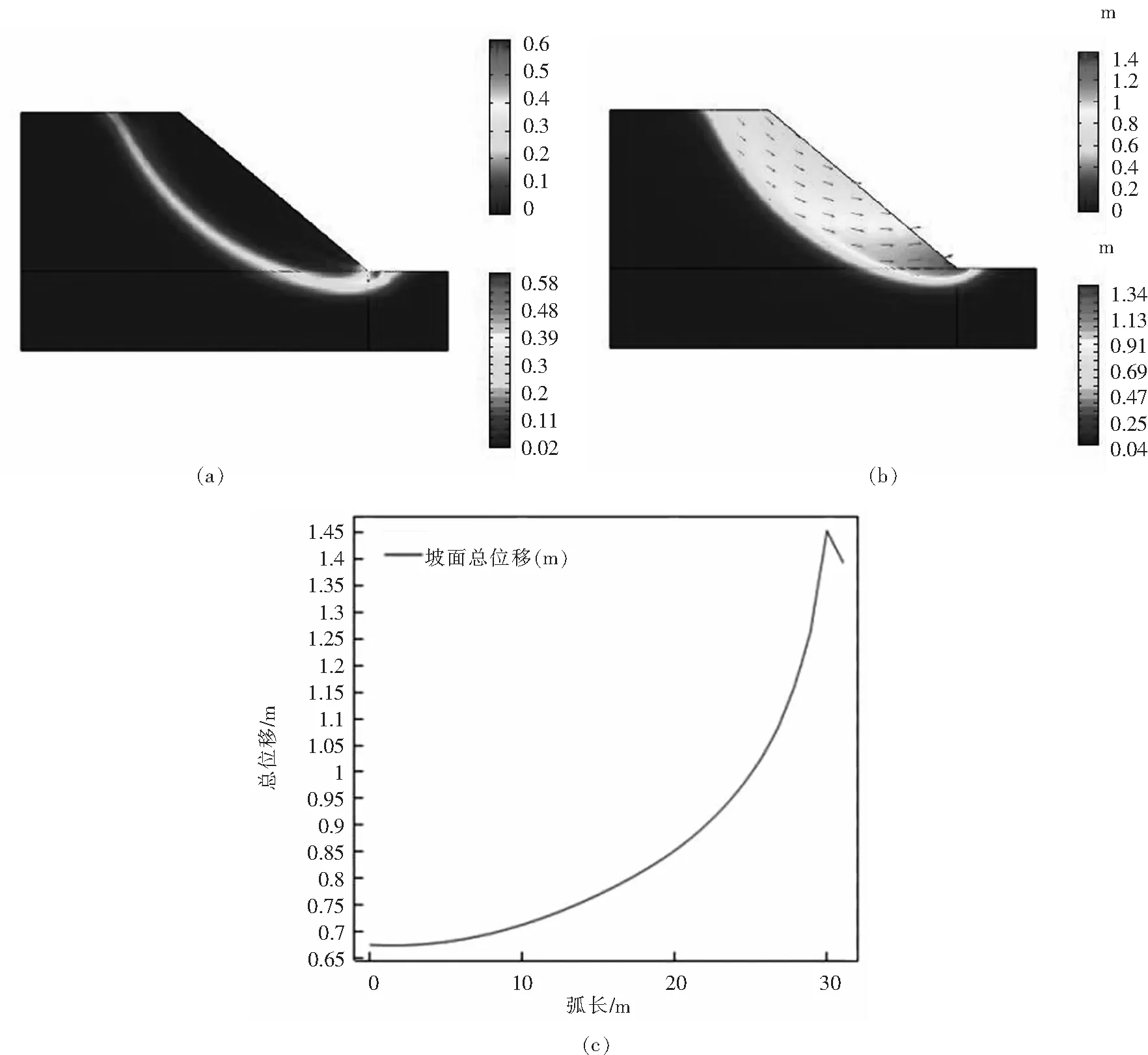
图17 耦合作用下土质边坡潜在破坏图Fig.17 Potential failure diagram of soil slope under coupling action
由图17可知,其中:(a)为有限元强度折减法计算后土质边坡有效塑性应变等值云图,(b)为位移等值云图,(c)为坡面位移曲线图.在结合有限元强度折减法计算后,可得到土质边坡在降雨-渗流-应力耦合作用下的潜在破坏面,所表现出的失稳破坏类型为滑坡破坏,其主要表现特征是边坡土体内部朝向坡面,由坡角延伸至坡顶处形成滑动弧面,折减后的安全系数为1.283,最小位移为0.04 m,最大位移为1.45 m,其中以坡角处位移最为敏感.
3 安全性分析
土质边坡的稳定性与其安全性密不可分,边坡稳定性是实现边坡安全性的前提,即要实现边坡安全性必须要先解决边坡稳定性问题.从安全学原理角度出发,将土质边坡发生的失稳破坏假定为事故,并将其划分为三个阶段,即事故孕育阶段、事故生长阶段、事故损失阶段,根据COMSOL Multiphysics软件对降雨-渗流-应力耦合作用下土质边坡稳定性数值模拟云图结果,可将土质边坡在降雨渗流前1.4 h定义为事故孕育阶段,此时天然土质边坡为低风险状态,较为安全;在1.4 h至边坡发生失稳破坏前定义为事故生长阶段,此时天然土质边坡为高风险状态,即较为不安全;在持续作用直至失稳破坏后,转变为事故损失阶段,此时事故已经产生,又将由不安全逐渐转变为趋于安全状态,即逐渐向低风险状态过渡,形成新的力学平衡状态.而从有限元强度折减法对安全系数的定义出发,土质边坡在降雨渗流120 h后的安全系数为1.283,按照安全系数大于1时为稳定状态,小于1时为不稳定状态的定义,理论上来说此时的边坡处于一个较为安全的状态,但随着降雨-渗流-应力耦合的不断作用,土质边坡持续受作用5天后的位移变形是直线上升的,发展速度快,且依据在现实生活中的实际情况,安全系数值只能作为一个参考,不完全符合实际,故而将降雨-渗流-应力耦合作用下的土质边坡定义为不安全状态.
4 结论
以天然土质边坡为研究对象,运用COMSOL Multiphysics数值模拟软件,通过构建几何二维平面有限元土质边坡模型,揭示了天然土质边坡在多物理场耦合作用下的演化规律,获取了在降雨-渗流-应力场耦合作用下天然土质边坡的安全性,结果表明:随着降雨渗流的不断进行,在降雨渗流前1.4 h,天然土质边坡的位移变形呈直线上升,此时天然土质边坡为低风险状态,处于事故孕育阶段,较为安全;在1.4 h至24 h为缓慢变形时间段,24 h后变形程度逐渐地加大,其中以坡角处变形最为明显,此时天然土质边坡为高风险状态,处于事故生长阶段,即较为不安全;在持续作用直至失稳破坏后,转变为事故损失阶段.通过有限元强度折减法对有限元模型进行了计算分析,在降雨-渗流-应力场耦合作用下,天然土质边坡潜在破坏面为滑动破坏,其主要表现特征是边坡土体内部朝向坡面,由坡角延伸至坡顶处形成滑动弧面,最小位移为0.04 m,最大位移为1.45 m,安全系数为1.283.
