汽车风阻系数灵敏度分析方法研究
2021-09-30苏东海
郑 鑫,苏东海
(1.沈阳工业大学机械工程学院,沈阳110870;2.华晨汽车工程研究院,沈阳110141)
前言
以前在汽车产品的设计初期,造型师不考虑整车的空气动力学性能导致新造型的车辆具有较大的风阻。近年来,由于国家对车辆的油耗法规越来越严格,车辆的空气动力学性能被高度重视。目前,传统汽车设计的流程是先设计车身空间布置、考虑美学和科技感设计,造型基本定型后,再进行空气动力学优化;为了考虑美学,空气动力学优化的空间变得很窄;考虑新产品开发的周期,预留给空气动力学优化的时间会变得很少;空气动力学在国内的发展不过20年,空气动力学工程师技术水平还有待进一步提升才能满足新产品的开发需求。基于以上问题,急需一种全新的空气动力学优化方法来缩短优化周期,完成空气动力学性能目标,提升企业产品竞争实力[1-8]。
应企业的急迫需求,本文中就此介绍一种全新的空气动力学优化方法,可以通过准确寻找到车身表面对风阻敏感的区域位置,获取相应的风阻敏感度值,确定相关位置或零部件的优化方向,快速完成整车空气动力学性能目标[9-15]。此方法也打破了对空气动力学工程师的技术门槛,科学有效地完成企业的空气动力学性能开发需求。
1 风阻敏感度分析方法介绍
1.1 关于风阻系数的灵敏度推导
整车车身造型对风阻敏感度分析可以采用全局敏感度分析法,也可用区域敏感度分析法或采用两种方法配合进行分析。采用全局敏感度法分析出影响风阻的主要敏感度位置或零部件,用区域灵敏度法分析出区域变化对整车风阻的影响效果。全局敏感度法比较适合用于车身造型设计的初期,进行整车的风阻敏感度分析。区域敏感度法适合于车身造型设计的中期,在较为敏感的区域内进行系统、准确的敏感度分析,寻找出更加具体的优化方向。
假设整车车身造型固定不变,整车风阻系数会受到风速、迎风面积和横摆角的影响,将风阻系数设为优化的目标,其目标函数为

式中:v为车辆运行速度,m∕s;A为车辆的正投影面积;α为横摆角,rad。在空气动力学中除了风阻系数,还需要考虑升力系数Cl,因为升力影响整车的操控性能,尽量让Cl变小或负数,保证车辆在运行过程中保持运动的稳定性。由于车辆在运动过程中会有转向,车辆就会有一定的横摆角存在,整车的风阻就会与横摆角为零的状态存在差别,则阻力系数目标值变化的表达式为

建立阻力系数和升力系数的关系式:

式中:λ为阻力系数和升力系数关系式的斜率,也是目标函数中针对Cd和Cl的影响程度比,
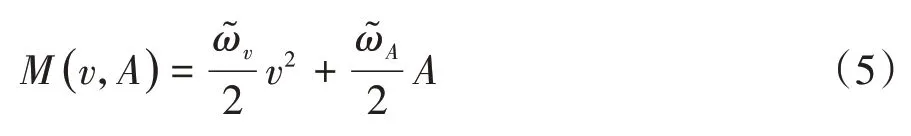
式中为敏感度系数。
经典的风阻系数计算公式为

式中F为整车风阻,N。
由式(1)可知,式(5)和式(6)相等,都是关于速度v和迎风面积A的函数。为了求出两个敏感度系数,分别对速度v和迎风面积A进行求导:

得到速度的敏感度和迎风面积的敏感度分别为
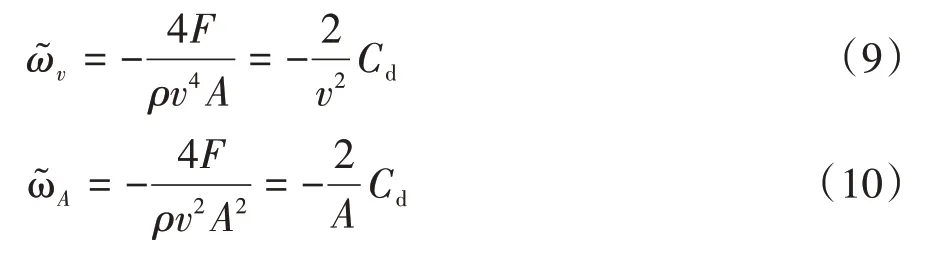
由式(9)可得到车辆的速度和风阻系数的灵敏度关系,当正投影面积不变时,风阻系数和速度的平方成负相关,即车速越大,整车的车速敏感度越小。当车速不断增加时,速度的敏感度将趋近于0,风阻系数不会再发生变化。由式(10)可得车辆的迎风面积和风阻系数的灵敏度关系,迎风面积的敏感度与车速没有关系,迎风面积越大,越小。
假定车辆沿直线作匀速运动,车辆的速度不变,横摆角为0,现针对整车车身造型进行空气动力学优化来进行风阻灵敏度分析。
首先进行全局灵敏度分析,设定输入变量是一个m维度的空间域Πm。
将风阻系数的目标函数M(x1,x2,…,xm)拆分为低维度的空间子集:

得到风阻系数的目标函数M(x1,x2,…,xm)的总方差:

经过推导,得到各阶灵敏度系数为

式中:Si为输入变量xi的1阶灵敏度系数,表示输入变量xi对输出变量的影响程度;Sij(i≠j)为2阶灵敏度系数,表示输入变量xi和输入变量xj之间的关联度;S1,2,…,m为m阶灵敏度,表示有m个输入变量之间的关联度。
可得到:
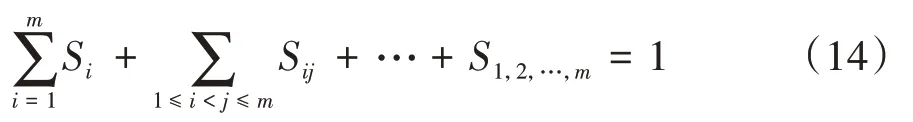
针对于区域灵敏度方法求解风阻系数的灵敏度。根据关于Xi的δ指标贡献(CDI),引入风阻系数的目标函数得到其表达式为
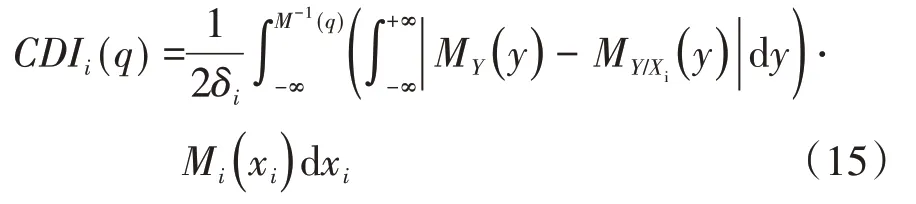
式中CDIi(q)的控制区域为[0,1]2。通过式(15)可以求出所有输入变量的δ指标贡献,即可分析出主要贡献因子的数量及其占比。
通过Copula函数法进一步简化式(15):
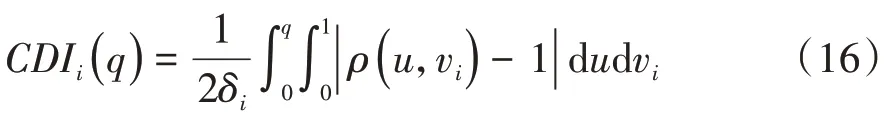
若Copula函数的密度ρ(u,vi)可以得到,则采用2阶数值积分就可求出CDIi(q),得到δ指标贡献。
1.2 自动变形技术理论推导
借助于计算机,可以从离散后的流场中计算得到计算网格表面即车身造型表面的灵敏度,可以通过设定目标值,限定输入变量的计算区域,就可完成准确的变形趋势计算,大大提升了风阻系数目标函数的计算精度。整个计算过程,充分考虑了问题的整体性,通过线性变化、矩阵求解等数学方法得到系统的离散型变形趋势模型,全面地剖析了变形趋势模型相对于传统模型的巨大优势,实现了计算的工作量与输入变量个数的无关性;实现了智能的微分技术对空间离散的计算,消除了由于计算的盲目性导致的大量无效计算量。
(1)下面基于流场变形趋势方程的变形趋势模型来求解相关表面网格,即车身造型表面的灵敏度分析。对于车辆的风阻系数优化,可以设定目标函数为

其中:

式中:Q为风阻系数;xsurf为车身造型面需要调整的网格点坐标;xall为车身造型面的所有网格点坐标;w为所有车身造型的网格点流场状态。
采用微积分中的链式法则对式(17)进行求导可得:


式中:[K]为刚度矩阵;Δxall为车身造型表面所有网格的位移;Δxsurf为车身造型表面需要调整的网格位移。该敏感度可表示为

令R为离散流场的方程残值。当仿真计算得到的流场稳定收敛时,存在R(w(xall),xall)=0,那么相应的流场可以进行线性处理,得到的方程为

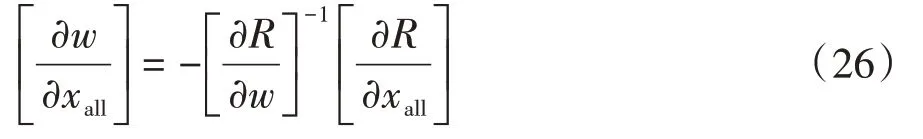
将式(24)和式(26)代入式(22)可以得到:
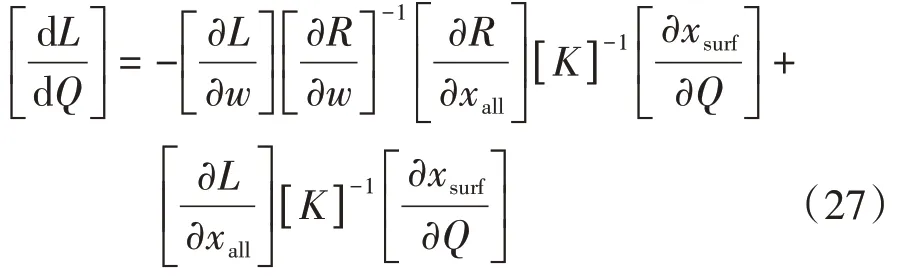
采用数学的转置运算法则,令Λ=为造型变化部分计算流场的变形趋势因子,变换后的流场变形趋势方程为

将式(28)代入式(27)得

式(29)就是基于流场的变形趋势模型。从式(28)和式(29)可以得到,虽然此基于流场的变形趋势模型与输入变量无关,但因为计算一个就必须对每个一输入变量计算一次动网格,同时还要参与复杂的矩阵方程求解。当输入变量较多时,计算时间将成倍的增加,这对计算资源提出了新的要求,为此基于流场的变形趋势方程模型要考虑在气动优化过程中的输入变量的选择。
(2)基于车身造型的风阻系数目标函数的全局变形趋势模型,由于基于流场的变形趋势方程模型需要每次计算动网格及复杂的计算过程,现对此变形趋势方程进行进一步处理,得到车身造型的风阻系数目标函数的全局变形趋势模型:
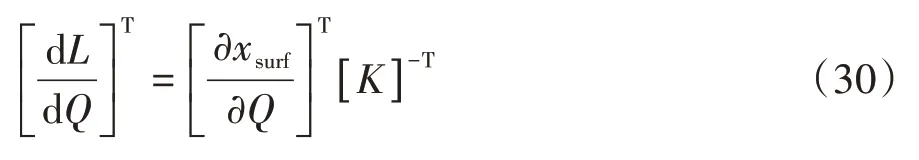

式(31)和式(28)相同,都是流场相关的变形趋势方程,Λw是整个流场的变形趋势因子。计算车身造型的风阻系数目标函数对所有车身造型表面网格坐标的敏感度


式(33)为变形趋势方程中的动网格部分,Λx为车身造型表面网格的变形趋势变量。通过矩阵方程的推导求出最终的目标函数梯度

基于车身造型的风阻系数目标函数的全局变形趋势模型中,由于对式(23)进行了矩阵的转置处理,使得与输入变量相关的项出现在式(30)的左侧,在整个计算过程中最后一步的计算才涉及了输入变量,保持了整个流程相关的变形趋势方程、变形趋势方程的动网格的求解以及相关的几何敏感度计算都与输入变量的无关性。通过这样的处理,整个模型的仿真可以实现自学习、自判断、自适应网格,同时计算精度也得到了保证。
2 对某款SUV进行风阻敏感度分析
2.1 敏感度分析
针对某款SUV的车身造型进行风阻敏感度分析,采用的模型为某SUV车型。本文中采用稳态计算,为了保持计算的稳定性,采用耦合求解器,通过适当增加库朗数(Courant number)设为200来提高计算的收敛速度。
边界条件设置好后,先计算一个稳定的流场,仿真的收敛性通过观察残差曲线来判断,残差曲线的检测值越低越好,一般在10-5以下为完全收敛。此时计算得到的风阻系数值作为实车风阻系数的近似值。
选取位于造型表面的控制点,如图1所示,对于控制点的选取可以根据工程师的经验来选择车身造型对风阻的主要贡献区域,这样可以快速、精确地完成风阻的优化。若只是流体工程师而非专业的汽车空气动力学工程师,可以根据车身造型的表面进行从车头到车尾全面覆盖选取,选取的距离最好贴敷车身表面,尽量靠近,目的是更快速、更精确地得到车身造型表面对整车风阻的影响,进而确认车身造型的优化方向,存在的缺陷就是选取的控制点较多,即输入变量较多,整个模型的计算时间也会增长,但由于采用基于车身造型的风阻系数目标函数的全局变形趋势模型计算,会很大程度上减少计算时间量,根据模型计算方法的选择对比计算,采用基于车身造型的风阻系数目标函数的全局变形趋势模型计算时间要比基于流场变形趋势方程的变形趋势模型可节省10%~20%的计算时间。

图1 车身造型表面的控制点
基于计算出的网格敏感度,造型表面网格将在每个控制点处发生曲面变形,其设置的指定控制点的位移量由最大值∕最小值来定义目标函数的敏感性,通常敏感度的程度定义为
$MaxDisplcement∕${MaxReport}
图2为整车控制点的位移敏感度矢量,矢量箭头的方向为车身造型优化的推荐方向。图中MaxDisplcement为8 mm,MaxReport是控制点的位置敏感度矢量的最大值。

图2 控制点的位置敏感度矢量
车身造型表面的网格敏感度如图3所示,红色区域表示敏感度的位移量达到1,这些区域对整车风阻的影响程度最高,车头、前发动机舱与前风窗玻璃夹角和车辆尾部是重点关注区域。车头是位于车辆的最前端,考虑到内部有散热系统、前端模块等零部件,优化的空间非常有限,故只考虑前发动机舱与前风窗玻璃夹角和车辆尾部的敏感度对整车风阻的影响。可见,灵敏度分析可以直观地寻找到对优化造型表面的主要影响区域或零部件,从全局角度进行整车灵敏度分析,灵敏度位移量最大的区域就是对风阻系数优化最见成效的区域。

图3 网格敏感度示意图
2.2 自动变形技术实现
采用变形技术是因为敏感度分析完成后,得到了车身造型表面的变化趋势,通过变形可以直观地得到降低风阻后造型面的变化情况,省掉了工程师根据经验去人为判断,极大地提升了空气动力学优化的智能性。
车身造型表面网格变形量的显示如图4所示,红色表示最大位移变化量,优化该位置的型面对降低整车风阻非常有利。前端的位移变化主要是前风窗的型面变化,红色的原点位置的弧度变化最大。同理,汽车尾部的车标位置的位移变化最大。

图4 网格变形位移示意图
通过敏感度分析后,找到了变形最大的位置,更加准确的车辆造型面变化情况如图5和图6所示。由图5可知,造型面的变化是向外突出的,这是由于通过增加前风窗玻璃型面的弧度,让通过前风窗玻璃的气流可以平顺通过,减少气流分离。由图6可见,计算一次车身造型表面网格敏感度后造型表面就会发生变化,整车的风阻系数就会完成一次优化,此过程可以进行多次,直到达到设计目标。车身尾部更向外突出,这样的好处在于气流通过车辆尾部时可以尽最大程度地贴敷车身,使脱离车身的气流分离延后,进而达到降低风阻的目的。手动变形可以直接影响车身造型表面的变化幅度,但几何结构特征容易受到破坏,而本文采用的变形方法在整个变形过程是自动化的,新生成的几何表面是非常平滑的,这里需要强调:在设计优化过程中,必须要考虑到项目对整车的定义,改变车辆长度一定要在合理的变化范围内才能进行。即在项目开发的早期比较容易实现。

图5 车辆前端模型的前后变形对比

图6 车辆后端模型的前后变形对比
通过灵敏度分析、网格变形后计算得到的风阻系数值如表1所示。其中:网络变形4见图5和图6;而变形1和变形3则依次介于原模型与变形4之间。

表1 优化过程中风阻系数值对比
原模型在Y平面上的速度分布云图如图7所示,车辆尾涡的区域较大,方向向上,气流的流动速度较大,导致整车尾部的压力较小,车辆前后的压差较大,风阻系数较大。通过多轮敏感度分析,网格变形后,整车的车身造型表面发生变化,优化后的整车速度流场如图8所示。对比图7和图8,优化后的整车顶部的速度明显增加,这表明通过前风窗弧面的优化增加了气流贴附车顶流动的距离,减少了车体表面的涡流区,即减小了车身表面的剪切力,所以在一定程度上对降低风阻有利。车辆尾涡的方向由向上变成向下流动,尾涡的面积减少,减少了尾涡对车身表面的影响,而且在一定程度上填补了尾部的空压区,这对降低整车的风阻系数非常有利。

图7 原模型的速度流场分布图

图8 优化后的速度流场分布图
3 风洞试验前准备及结果分析
3.1 风洞试验前准备
本次试验得到了宝马的支持,在宝马工作间用油泥制作试验样车,需要强调:油泥模型的车架为刚制骨架,表面包覆ABS材料制作的原车车型的近似形体,最外面包裹油泥。图9为车辆骨架的设计图,此骨架具有平台通用性。图10为ABS材料制作的车身外形,表面上的孔洞主要起到固定油泥的作用。图11为ABS表面粘贴油泥、最外层采用高精度三维数字铣刀加工整车造型。图12为真实的散热风扇。图13为轮罩附近的结构,完全按照真实数据制作。图14为整车在风洞中进行安装调试的场景。
图9 车辆骨架设计图

图10 ABS车身

图11 表面油泥模型

图12 散热风扇

图13 轮罩附近结构

图14 测试车辆风洞试验图
3.2 风洞试验结果分析
根据智能优化的影响因子建立风洞试验测试的优化方案,具体的试验结果与仿真对比见表2,可以得到以下结论:
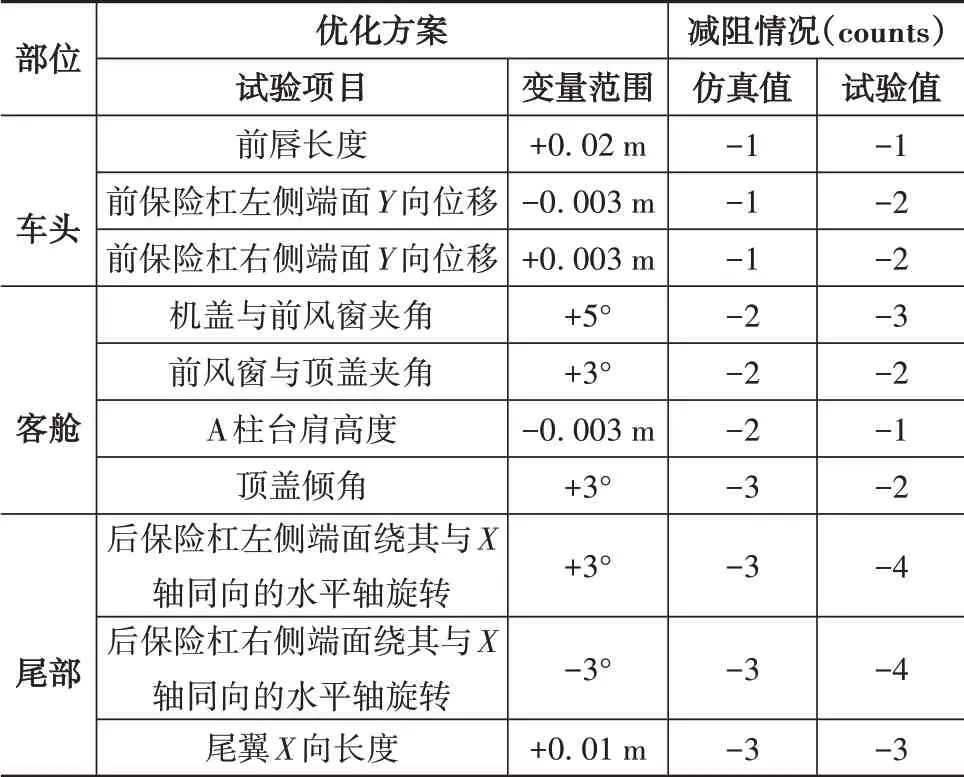
表2 整车风阻影响因子分析结果表
(1)从试验和仿真结果对比,仿真误差较小;
(2)尾部优化对风阻系数降低效果最明显,设计过程中着重针对尾部做优化;
(3)风洞试验的全过程都有造型师的参与,让造型师零距离接触风洞试验,了解影响车辆空气动力学特性的车身造型关键位置,便于以后造型设计过程中着重考虑。
4 结论
通过本文中的研究,得到以下结论。
(1)完成风阻灵敏度的理论推导,实现了灵敏度在空气动力学风阻计算中的理论推广。
(2)自动变形技术可以使整个模型的仿真实现自学习、自判断、自适应网格,同时计算精度也得到了保证。
(3)通过对某SUV的风阻敏感度分析,运用网格变形技术实现网格针对敏感度的变化,实现风阻系数优化结果的全自动输出。证明了风阻灵敏度理论和自动变形技术的可行性。
(4)计算全过程无需人工干预,就可达到预设风阻系数目标值。
