感应式磁力仪MFS06e的磁场记录时域分析

蒋 礼

(华北水利水电大学数学与统计学院，河南 郑州 450046)

德国Metronix公司的电磁测深系统GMS由于精度高、操作方便等优点而在高校、科研院所及生产单位中得到了广泛应用[1-3]。国内目前常用的型号为GMS07[4]，该系统通常由一台主机ADU07、磁场传感器MFS06e[5-6]、固体不极化电极和联接电缆线所组成。但是非常遗憾，由生产商提供的系统操作软件Mapros，仅能显示磁场传感器的原始感应电压(单位为mV)，以及最终的阻抗张量估算结果，而无法显示真实的磁场值[4，7]。这给使用者带来了诸多不便，比如:不同仪器间的一致性检测，不能直接使用实测磁场记录，而只能使用阻抗张量[8-9]；仪器的重新标定必须返厂由生产商进行操作[10]；科研人员只能使用生产商的指定算法，无法对算法改进[11]。其他厂商的同类型仪器，大多也同样存在上述问题。

仅知感应电压无法直接估算出磁场值，必须使用标定函数或标定文件来去除仪器响应，才能得到真实的磁场记录(nT)[12]。由此导致，许多科研工作者在展示磁场记录时，要么无量纲[13]，要么直接使用感应电压值[14-15]，或者将感应电压和最终阻抗结果并列[4，16]，甚至会出现将感应电压记录误当作磁感应强度的情况[17]。

1 感应式磁力仪的频率响应函数

将磁场传感器作为一个系统，则磁场是系统的输入，感应电压是系统的输出。该系统的频率响应函数称为系统标定[10，18]，其决定着对不同频率输入信号的增益及延迟。如果能够获知系统标定，则根据感应电压来反演实测磁场，就可以转换成为一个已知输出和系统而求输入的问题。下面，以感应式磁力仪为例，分析该磁场传感器系统的频率响应函数。

基于法拉第电磁感应定理，感应式磁力仪的主线圈感应电动势为[19-20]:

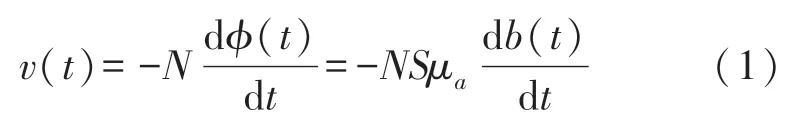
在式(1)中，N为线圈匝数，S为线圈截面积，μa为磁芯的有效磁导率，b(t)为线圈中的磁感应强度，φ(t)为线圈的磁通量。对式(1)进行傅里叶变换，可得:

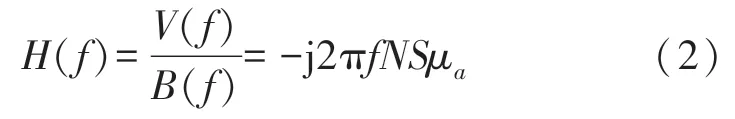
在式(2)中，f为频率，V(f)和B(f)分别为v(t)和b(t)的频谱，H(f)为主线圈的频率响应函数。为提高磁场观测带宽，还需要在主线圈上引入磁通负反馈[19]:

式中:G为放大器增益，M为主线圈与反馈线圈的互感，Rfb为反馈电阻，Lp为主线圈等效电感，C为等效分布电容。如此，感应式磁力仪的总频率响应函数为:Cal(f)＝H(f)·H0(f)，Cal(f)也被称为该磁场传感器的标定。另外，由于运算放大器的1/f噪声对线圈的低频信号干扰严重，所以通常还需要在传感器中使用斩波稳零技术来改善低频段信号[20]。

下面，以GMS系统常配置的感应式磁力仪MFS06e为例，分析其具体的标定。

2 磁力仪MFS06e的标定分析

磁场传感器的标定分为两类:标定文件和标定函数。标定函数由物理原理和制作工艺决定，相当于该系统的理论频率响应函数，同一型号的传感器的标定函数完全一致。标定文件则对应于每一个传感器的实际频率响应函数，由于电子元器件及零部件参数的细微差异，同一型号的两个传感器的标定文件也不可能完全一样。

模型记录各类别的碎片信息出现的频率、时间甚至地点等，然后根据这些经验分析哪个时间段，哪个地点适合推送什么类别的语义图示。机器学习通过先向学习者推送未聚类的知识变量使学习者根据知识特征进行手动聚类，并将结果与机器学习的聚类结果进行匹配，就能发现学习者可能遗漏或者不确定的知识点，这些反馈信息就代表学习者还需努力进步的方向。学习者可以根据自身要求将某些知识变量设置不同的重要等级。

2.1 标定函数

根据Metronix公司提供的MFS06e产品手册，该传感器的标定函数如下[18]:

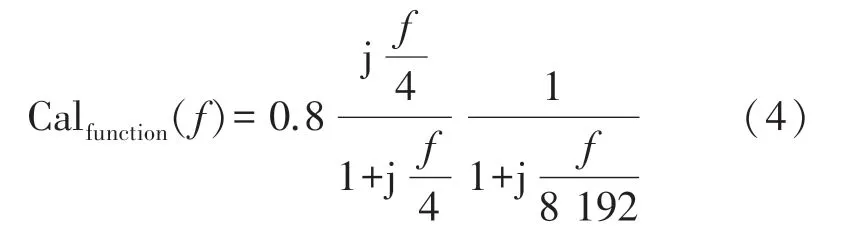
在进行去仪器响应时，标定函数Calfunction(f)可以直接当作该仪器的频率响应函数。所以，在已知磁场传感器的感应电压记录时，使用标定函数可以反演出真实的磁场值:

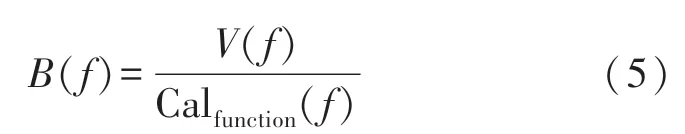
在式(5)中，V(f)和B(f)分别为感应电压记录和磁场值的频谱，对B(f)进行傅里叶逆变换即可得到传感器所测的真实磁感应强度b(t)。

2.2 标定文件

每个传感器都有自己特定的标定文件，文件名通常为“型号＋编号”，存放位置一般位于Mapros工区的Cal子文件夹中。表1为MFS06e046传感器的出厂标定文件的具体内容。由于打开斩波器可以改善低频信号，所以斩波器开(Chopper on)与关(Chopper off)的频率响应函数，在低频段差异显著[21]，因此生产商会分开进行标定[18]。为节省篇幅，在表1中将chopper off和chopper on的相同频点进行合并显示，并省略了部分频点的标定内容。

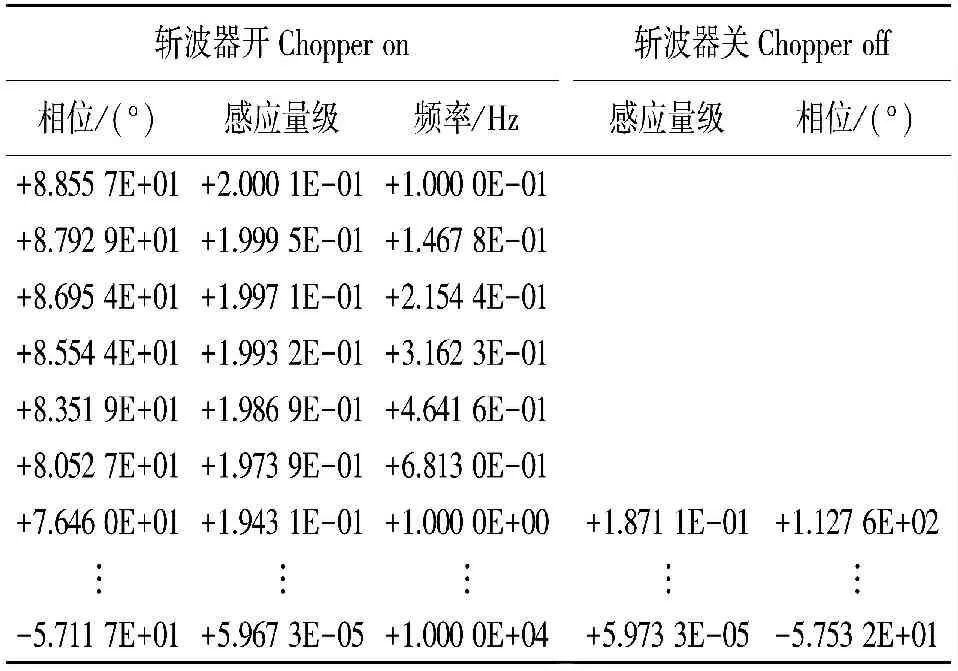
表1 MFS06e046的标定文件

在表1中，点线方框为chopper off时的标定，而虚线方框为chopper on时的标定，两者共用对应的频点值。标定文件通常分为三列，依次为频率、感应量级和相位，表中的所有数值均使用科学计数法来表示，取5位有效数值。从表中可以看出，频率的单位为Hz，各频点呈对数分布，其中chopper on的频点范围为104Hz~0.1 Hz，chopper off的频点范围为104Hz~1 Hz；相位的单位为度，表示对应频点的标定相位；感应量级的单位为V/(nT·Hz)，表示对应频点的标定幅度与该频率之商。从表中可以看到，随着频率的持续降低，chopper on标定的相位趋向于90°，而感应量级趋向于常量0.2。

由标定文件确定的系统频率响应函数如下:

在式(6)中，Mag(f)和Pha(f)分别为该频率值对应的感应量级和相位。

2.3 标定函数与标定文件对比

对于同一传感器，由标定函数和标定文件分别确定的频率响应函数间会存在一定的差异。图1为标定函数和标定文件的频率响应曲线对比图。

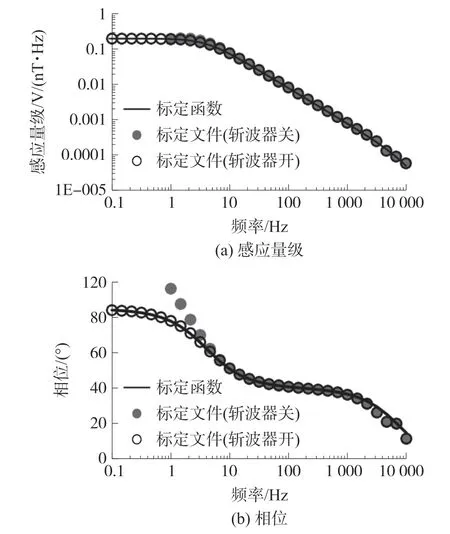
图1 MFS06e046的标定函数和标定文件的频率响应曲线

通过上述对比可以发现，虽然使用标定函数和标定文件都能将电压记录(V)转换为磁场记录(nT)，但是两者存在一定的差异。①在全频段，标定函数都可以近似代替标定文件中的chopper on；②在大于4Hz的频段，标定文件中的chopper off和chopper on具有同样的标定效果；③在小于4Hz的频段，只有选择chopper on来激活放大器的chopper放大技术，才能获得正确的标定结果；④在3 kHz~10 kHz的高频段，使用标定函数会出现一定的相位偏差，极个别频点可能会有近10°的偏差。

3 标定实验

图2为一段由装配3个感应式磁力仪MFS06e的GMS07系统所采集的时长约为25 min的磁场三分量记录，其中，图a为感应电压记录，图b为磁场反演结果。在图2中，a、b两幅子图的对应分量排列顺序完全一样，由上至下依次为:Bx、By和Bz，分别对应于磁场的北向、东向和垂向分量；而且所有子图的横轴均为时间轴，单位为“分”；a子图中的纵轴为电压，单位为mV；b子图中的纵轴为磁感应强度，单位为nT。观察图a中Bx、By和Bz的电压记录可以发现，在8分~11分、11分~16分以及16分~20分的三个时间段内，波形的频率明显不同，为描述方便，在文中依次将其称为高频段(HF)、低频段(LF)和中频段(MF)。图b为去仪器响应之后的磁场记录，其中实线为使用标定函数的结果，而虚线是使用标定文件中chopper on的结果。

3.1 时间序列的整体趋势对比

观察图2(b)的磁场记录可以发现，使用标定函数和标定文件的去仪器响应结果，在整体上相似程度极高，两者除了在趋势上有一点区别之外，无论是幅度的大小还是变化规律都基本一致。此外，两磁场反演结果的相位略有差别，标定函数(实线)较标定文件(虚线)的结果略有所超前。

但是，LF、MF和HF之间在图2(b)中的比例与在图2(a)中的比例明显不同。观察图2(a)的电压记录的振幅可以发现，在Bx分量中，MF的幅度最强，其次是LF，最弱的是HF；而在By分量中，LF的幅度最强，其次为MF，最弱的是HF；而在Bz分量中，LF的幅度最强，其次是HF，最弱的是MF。而对于图2(b)的磁场记录，在Bx分量中，LF和MF的幅度基本相当，HF几乎消失；在By分量中，LF的幅度明显高于MF，而HF非常微弱；在Bz分量中，HF和MF的幅度基本相当，但LF的幅度明显高于两者。

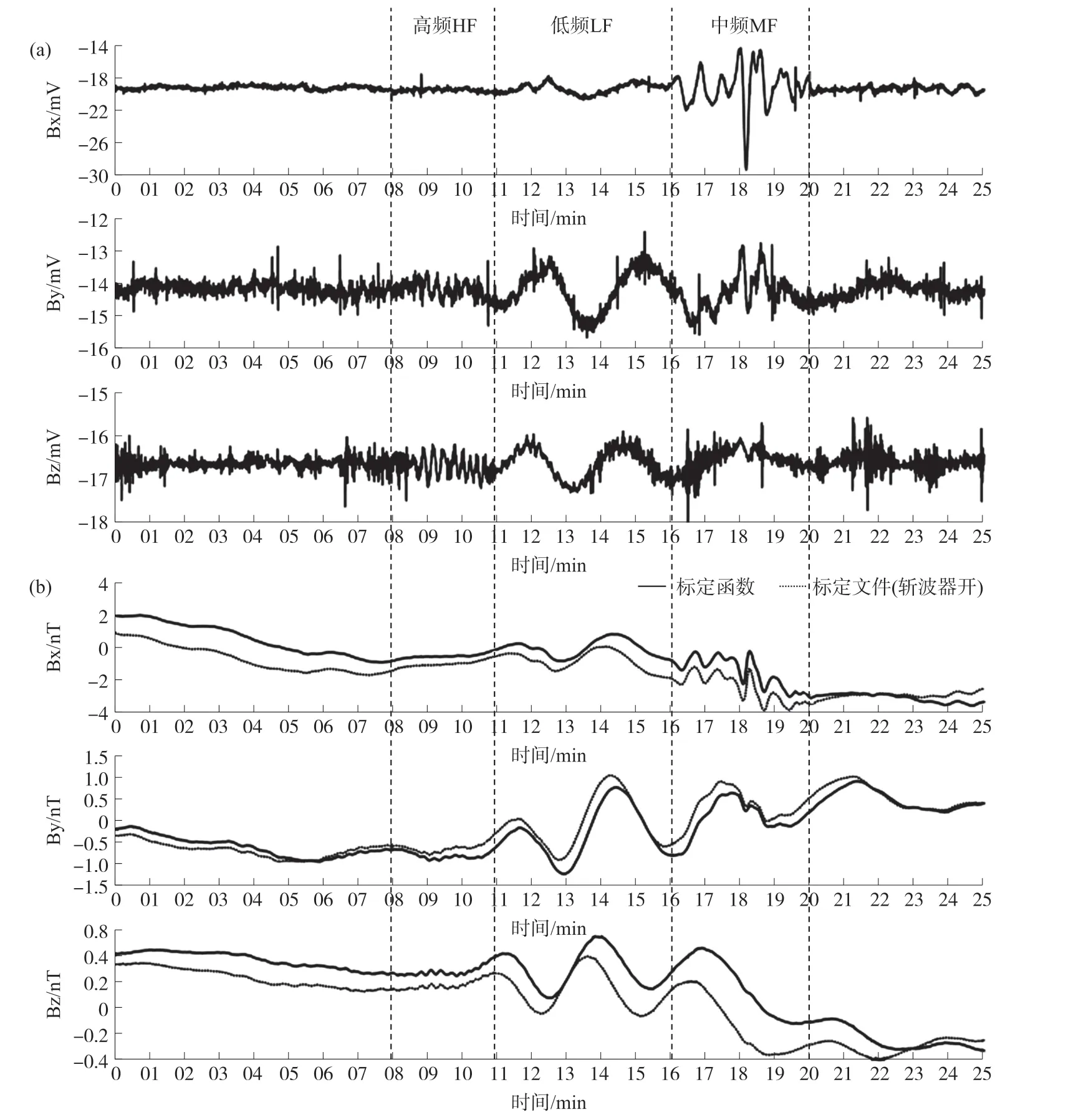
图2 MFS06e的原始电压记录及对应的磁场记录

由此可以看出，使用标定函数或标定文件去仪器响应时，将时间序列由mV转换为nT，对不同频率的补偿效果并不一样。电压信号的频率越低，所得到的补偿将越大。如此补偿后，低频信号相较高频信号而言，幅值增加更为明显。

3.2 时间序列的局部细节对比

为了进一步精确比较标定函数和标定文件的处理结果之间的差异，截取图2(b)所示磁场的局部时段和频段进行对比分析。对图2(b)中各分量的时间序列进行带通滤波，滤波参数统一为1 s、5 s、40 s、55 s(s表示“秒”，其中5 s和40 s为通带截止频率，而1 s和55 s为阻带截止频率)，以此提取出HF在18 s附近的主频信号，最后截取HF在8分~11分的主时段，由此可得图3。

图3的分量排列顺序及图标设置与图2完全一致。从图3可以看出，由于使用了带通滤波器，所以在各分量中，标定函数与标定文件的结果在趋势上已经没有任何差别，幅度变化几乎完全一致，只是在相位上略有区别。图中的实线略微滞后于虚线，这与图2(b)中的相位差异恰好相反。

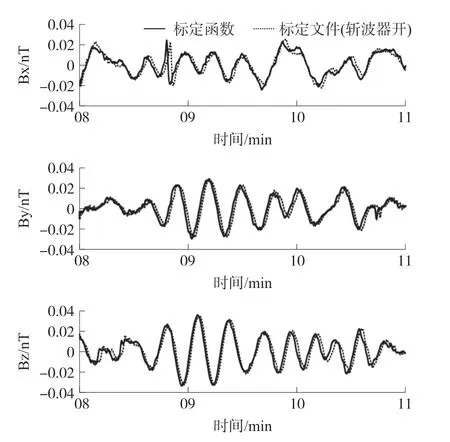
图3 由标定函数及标定文件分别反演的磁场记录

产生上述相位差异的原因，主要源于图1所示的标定函数和标定文件的频率响应曲线之间的差异。在图1(b)的高频部分，可以清楚的看到，标定文件的相位小于标定函数的相位，去仪器响应的过程是在频域中除以系统的标定，所以使用标定函数会产生更大的延迟。而随着频率的降低，根据式(4)，标定函数的相位趋向于90°；但是标定文件的最低频率只到0.1 Hz，对于更低频率的标定全部需要进行插值。从表1的chopper on中可以看出，随着频率的降低，虽然相位的增长速度越来越慢，但是照此趋势进行插值，必然会在某个低频点之后出现相位大于90°的情况，所以在低频段反而是标定文件的相位大于标定函数的相位。因此，去仪器响应之后，在低频部分，标定文件的结果较标定函数而言将会显得更为滞后。

4 结论

①使用标定函数和标定文件，都可以将感应式磁力仪MFS06e的电压记录，转换成真实的磁场记录；②使用标定函数的算法更简单，使用标定文件的结果更精确；③一般情况下，可以使用标定函数来代替标定文件，如此，系统的幅频特性基本是准确的，但相频特性可能会在局部频段上出现细微的偏差；④无论是使用标定函数还是标定文件去仪器响应，磁场记录都有可能出现相位超前或滞后的情况，需要针对具体频段、具体时段进行具体分析。

以上四点结论也可以推广到其他型号的感应式磁力仪，但对于其他类型的磁力仪(如:磁通门磁力仪[22])是否适用，还有待进一步验证。