基于磁通量法索力测量模型参数的调适研究*

2021-09-29刘小锋冯志敏胡海刚冯少玉徐俊峰

传感技术学报 2021年7期

刘小锋，冯志敏，胡海刚，冯少玉，徐俊峰

(宁波大学海运学院，浙江宁波 315832)

桥梁作为海洋工程中一项基础设施，对促进我国经济发展、便利人们生活方面发挥着十分积极的作用。拉索桥是当前较为常见的桥型，其中，拉索作为其主要承载构件，索力直接控制着整桥内力分布与线形。在桥梁长期运营过程中，重复变化的动载荷又将使拉索产生疲劳损伤，极大地威胁着桥梁的安全性与稳定性[1-3]，因此精确测量索力可为桥梁运营维护管理提供有力的参考依据。

目前，索力测量的方法主要有油压表法、压力传感器法、振动频率法和磁通量法等，相比于其他几种方法，磁通量法具有精度高、动态性好、寿命长、可实现全天候测量等诸多优点[4-7]，现已得到广泛地应用和研究。龙跃[8]、邓年春[9]、Zhao Y[10]、何利[11]、殷鹏雷[12]、Cho S[13]等分别利用磁通量传感器对天津永和大桥、湛江海湾大桥、香港昂船洲大桥、宜宾长江大桥、台州椒江二桥、韩国Hwamyung大桥进行索力监测，测量精度平均在3%左右。磁通量传感器在使用前需预先标定，以获得索力与感应电压间的模型关系。标定时，通常只对拉索进行单次逐级加载，以得到标定样本。然而，拉索卸载后，再次对其逐级张拉，获得的标定样本会与第1次标定样本间存有差异[14]，故单次标定模型精度稳定性较低。为此，徐聪[15]、任亮[16]、Cappello C[17]对试件进行3次循环加载，并取标定样本均值拟合模型，在一定程度上提高了模型精度的稳定性。虽然平均标定法运算简单，但却不能充分利用每组标定样本信息，造成了一定的信息资源浪费；此外，平均标定法的模型参数在实际索力测量时保持固定不变，故难以保证标定模型对每次随机测量均能达到较高精度。因此，对拉索进行多次加载标定，并充分挖掘每组标定样本信息，使模型参数随每次测量能够被适应性地调整，将对进一步提高索力测量精度及稳定性具有重要意义。

本文提出模型参数调适方法，分别对各组标定样本线性拟合，基于交叉测试和最近距离分配方法，使得实测感应电压可自适应地选择模型参数计算索力，每组标定样本信息都得到了充分利用。室温18℃时，在试验机上对15.2 mm钢绞线多次加载，并利用磁通量传感器测量对应感应电压，共获得4组标定样本和15个随机测试样本。基于获得的实验数据，对单次标定、平均标定和模型参数调适法进行测试、对比和分析，验证了模型参数调适法具有更高的测量精度及稳定性。

1 磁通量法索力测量原理

当铁磁材料在受到外力作用时，内部磁特性(如磁导率)将发生改变，此称为铁磁材料的磁弹效应[18]。拉索一般是由多根预应力钢绞线组成，属于铁磁材质，磁通量法正是基于拉索的磁弹效应利用磁通量传感器来测量索力。安装于拉索上的磁通量传感器一般为套筒式，其主要由励磁线圈、感应线圈、对应线圈骨架、外壳等组成，结构如图1所示。

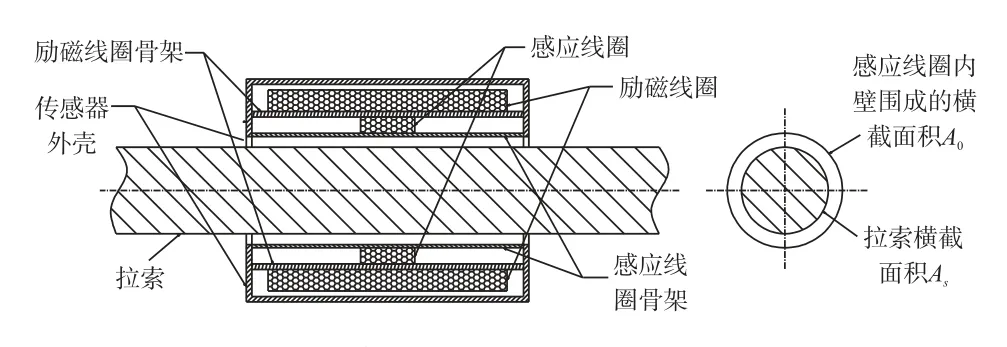
图1 套筒式磁通量传感器结构

磁通量传感器工作时，励磁线圈以一定频率对拉索进行励磁，感应线圈产生相应的感应电压。其中，感应电压大小取决于单位时间内通过感应线圈的磁通量，而磁通量又与线圈铁芯的磁导率有关。拉索作为线圈铁芯，其磁导率计算公式为[19]:

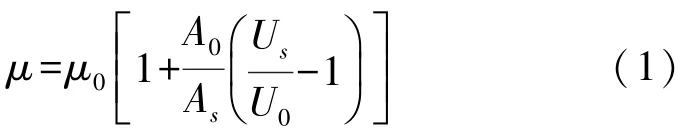
式中:μ为拉索磁导率、μ0为真空磁导率、As为拉索横截面积、A0为感应线圈内壁横截面积、Us为感应线圈中含拉索时的感应电压、U0为感应线圈中不含拉索时的感应电压。

当拉索受到轴向拉力时，磁导率将发生变化，由式(1)可得:

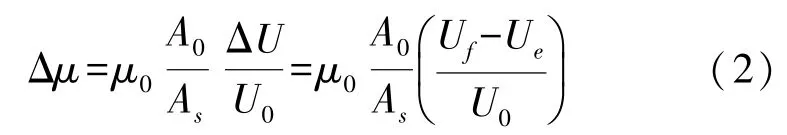
式中:Δμ为拉索磁导率变化量、Uf为拉索承载时的感应电压、Ue为拉索空载时的感应电压。

根据Joule效应，得拉索轴向应变与磁导率变化量间的关系为[20]:

式中:ε为拉索轴向应变、l为拉索长度、Δl为拉索轴向伸长量、λs为轴向变形常数、Ms为饱和磁化强度、H为外磁场强度、Kμ为单轴磁各项异性常数、θ0为磁场与易磁化轴间角度。

再由应力应变间关系得:

式中:σ为拉索横截面应力、E为拉索材料的弹性模量、F为索力。

联立式(2)~式(4)，得索力与感应电压间的关系为:

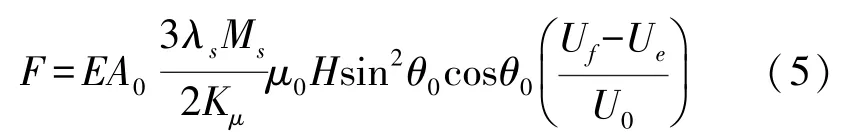
由式(5)可知，F与Uf间具有线性关系，斜率和截距参数通过标定获得。

2 模型参数调适法

为充分挖掘多组标定样本信息，并使标定出的模型参数随实测感应电压作适应调整，提出了模型参数调适法。该方法首先利用最小二乘法对各组标定样本线性拟合，确定各模型参数，再对各拟合模型采用其他组标定样本交叉测试，从而获得各模型参数下每级测试误差均值，然后根据实测感应电压与各组标定样本同级感应电压距离之和，找出最小距离对应级次以及该级次下交叉测试时最小误差均值对应模型参数，最后将实测感应电压代入此参数下模型计算索力。模型参数调适法的具体步骤如下:

①令第i组标定、第j级加载获得的感应电压与索力样本为(Uij，Fij)，i＝1，2，…，m；j＝1，2，…，n。其中，m为标定组数、n为加载级数。

②基于最小二乘法，线性拟合第i(i＝1，2，…，m)组标定样本集{(Uij，Fij)，j＝1，2，…，n}元素，确定模型参数ki、bi，得索力与感应电压间第i个标定模型为:

③将第c(c≠i，c＝1，2，…，m)组标定样本集{(Ucj，Fcj)，j＝1，2，…，n}中的Ucj代入式(6)中的U，得相应测试索力为:

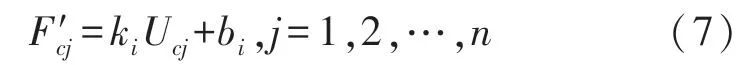
④计算集合{F′cj，j＝1，2，…，n}中各元素相对误差为:

⑤计算除第i组标定样本各级的测试索力平均相对误差为:

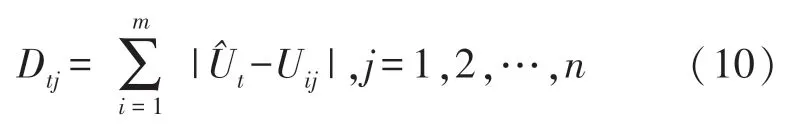
⑦找出集合{Dtj，j＝1，2，…，n}中最小值元素对应的指标j，取步骤5中j值下各模型的，得集合，i＝1，2，…，m}。

模型参数调适法流程如图2所示。

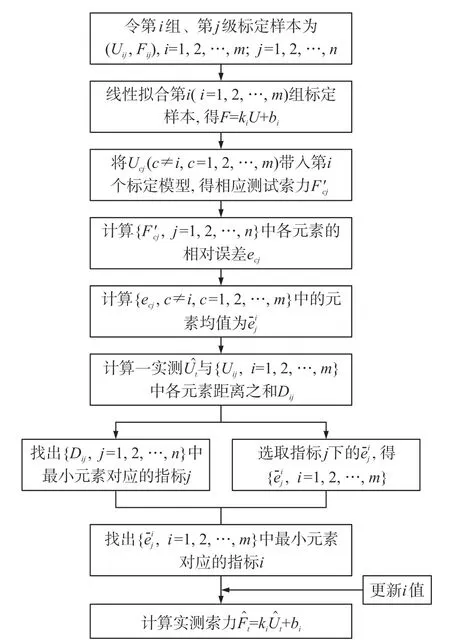
图2 模型参数调适法流程图

由此可知，模型参数调适法利用标定样本对各模型交叉测试时的最小误差均值来确定每级最优模型参数，并基于聚类思想，以实测感应电压与标定感应电压最近距离对应级次来分配模型参数，故当标定样本选取的足够均匀合理时，该方法将对实际工程中索力测量精度提高十分有益。

3 实验与分析

3.1 实验方法

将磁通量传感器安装固定到一段钢绞线上，再将钢绞线两端安装于试验机上下夹头中。在室内某温度下，利用试验机以一定步长对钢绞线逐级加载至设定值，同时利用磁通量传感器测量出钢绞线在各级加载下的感应电压，按此过程循环测量多次，获得多组标定样本，并将它们取均值，作为新的一组标定样本。再对钢绞线随机加载，获得多个测试样本。根据获得的实验数据，分别对单次标定、平均标定、模型参数调适法进行测试，通过对比分析测试结果，验证模型参数调适法的可行性和有效性。

3.2 实验条件及数据获取

实验选用钢绞线长度为700 mm、直径为15.2 mm，磁通量传感器由深圳某公司生产，内径为17 mm、外径为45 mm、长度为210 mm，试验机由长春机械科学研究院有限公司生产，最大拉力为100 kN，实验系统如图3所示。在室内温度18℃下，利用试验机以2 kN为步长对钢绞线从0 kN逐级加载至30 kN，同时利用磁通量传感器测量各级加载下的感应电压，按此过程循环3次，共获得3组标定样本，再取3组标定样本的均值作为第4组标定样本，各组标定样本如表1所示。再对钢绞线进行15次随机加载测量，共获得15个测试样本，如表2所示。

图3 磁通量法索力测量实验系统

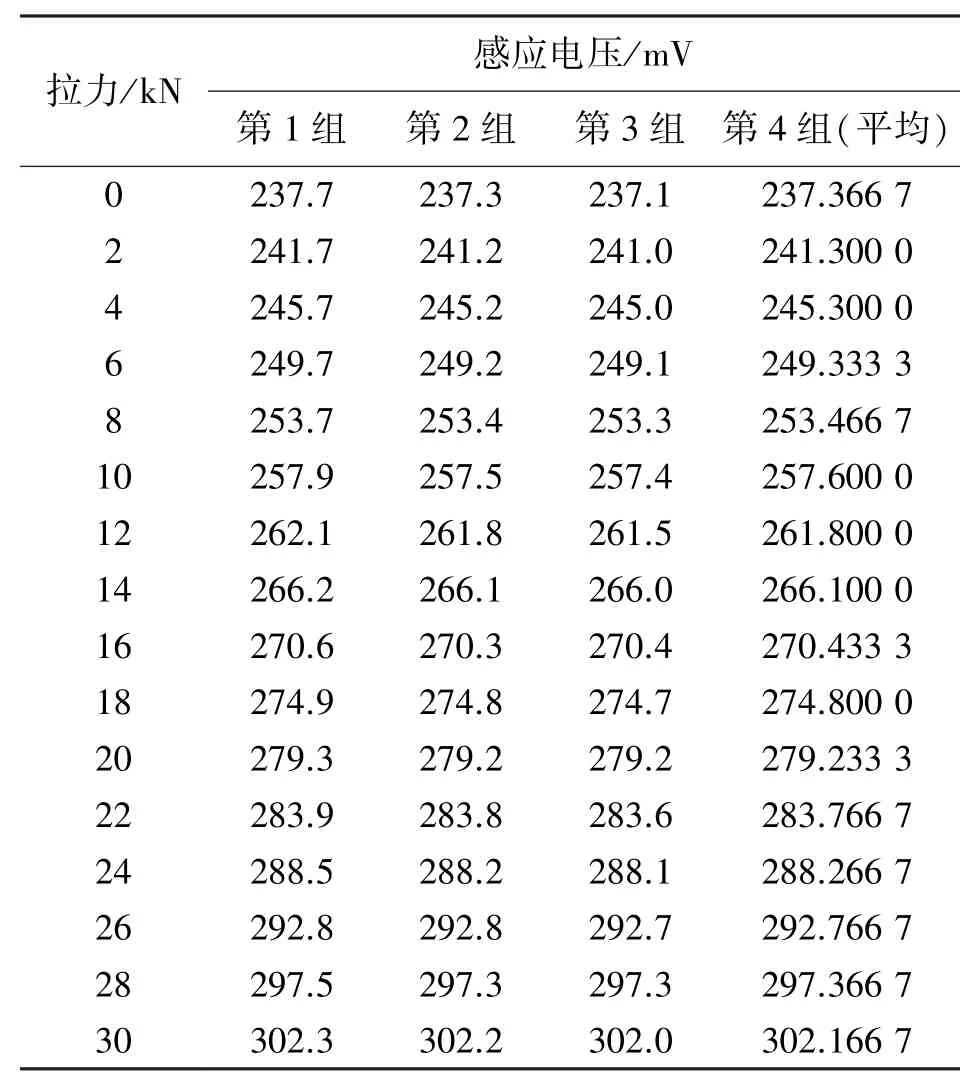
表1 标定样本数据

表2 测试样本数据

3.3 测试结果及分析

利用最小二乘法分别对4组标定样本线性拟合，结果如图4所示。从图中可看出，各拟合线均能很好地通过样本点，相关系数也都在0.999 6以上，说明拉力与感应电压间具有高度的线性正相关关系，符合磁通量法测量理论，同时也表明磁通量传感器工作正常。4个线性模型的斜率k和截距b如表3所示。表中可知，各模型参数间均有差异，故对应的拉力测量结果也必将不同。

表3 四个线性模型参数值

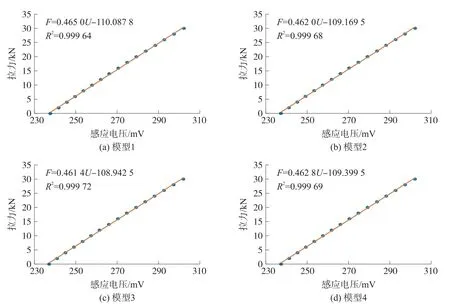
图4 四个线性模型

利用上述4个模型对15个测试样本进行测量，对应的测量误差如图5所示。由图5可知，各模型测量误差不同，在一些测试样本处还存有较大差异，且各模型精度随测试样本不同而变化，表明单次标定模型的精度稳定性较差；此外，模型4虽具有稍好的精度稳定性，但对每个测试样本并不具有最高测量精度，即若直接利用平均标定法来获得最终测量模型，必将导致精度较高的其他模型被弃用。因此，对于每个测试样本，应选择合适的模型参数，以获得较平均标定法更高的测量精度及稳定性。

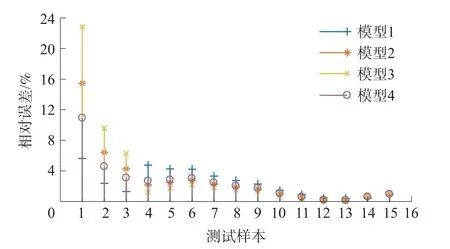
图5 四个模型的测量误差

利用模型参数调适法对15个测试样本测量，其中每个测试样本所选取的模型参数如表4所示。表中可知，模型参数调适法的模型参数随测试样本动态变化，表明模型参数调适法可根据实测感应电压来对模型参数进行适应性选择。

表4 测试样本模型参数选择表

将模型参数调适法与平均标定法的测量结果及误差进行对比，结果如表5所示。表中可知，模型参数调适法的测量误差都低于平均标定法，表明模型参数调适法对提高测量精度取得了显著效果；此外，经表中计算可得，模型参数调适法与平均标定法测试误差的均值分别为1.507 5%和2.469 0%，表明模型参数调适法的精度比平均标定法提高了1.6378倍；模型参数调适法与平均标定法测试误差的标准差分别为1.371 1和2.661 5，表明模型参数调适法的精度稳定性比平均标定法提高了1.941 1倍。

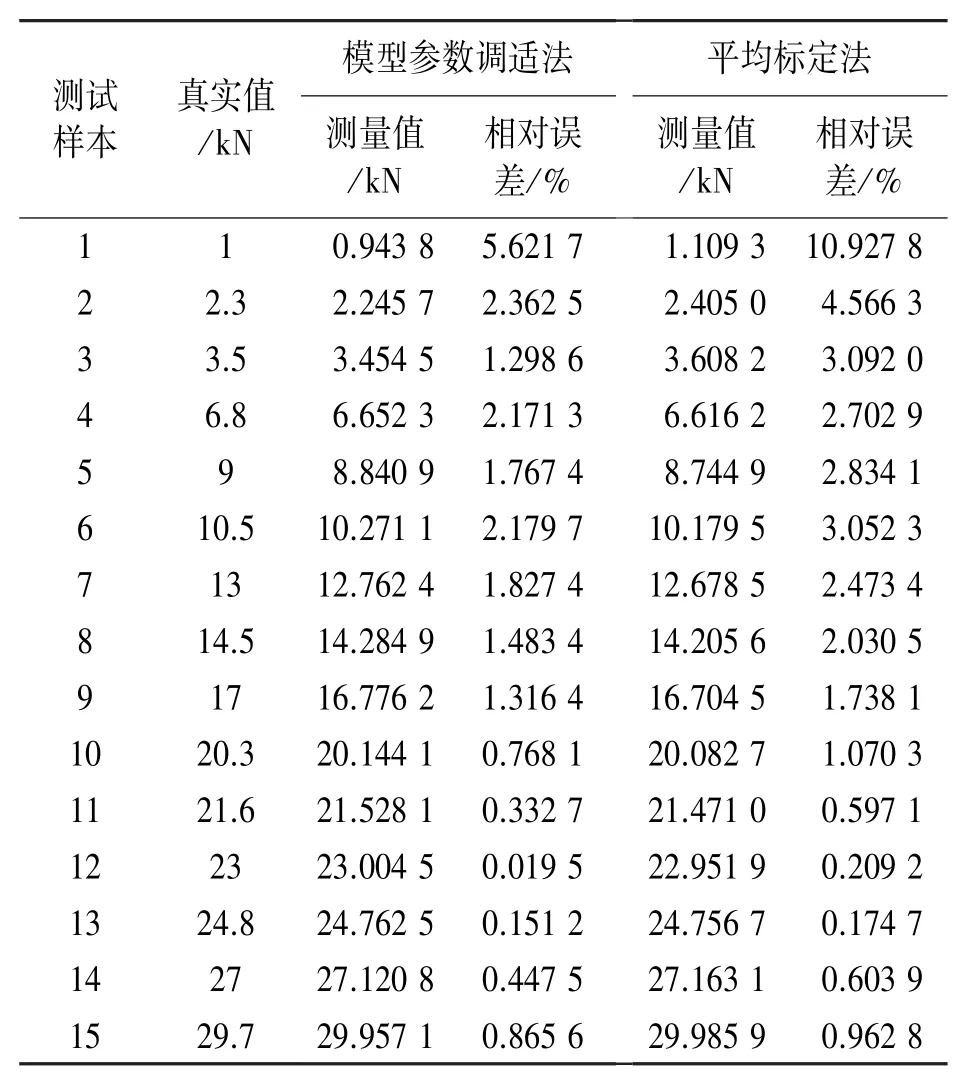
表5 模型参数调适法和平均标定法的测量结果及误差对比

综上所述，由于各单次标定模型参数不同，使得一些测量误差存有较大差异，平均标定法虽综合了每次标定样本信息，获得稍好的精度稳定性，但因对信息利用率较低，精度并没有达到最高，而模型参数调适法可根据每次实测感应电压适应性地选择合理的模型参数，使每组标定样本信息均得到充分利用，相应地减小了测量误差，从而较平均标定法提高了测量精度和稳定性。