基于CEEMDAN阈值滤波的磁场信号去噪模型*

董晓芬，陈国光，田晓丽，闫小龙，赵归平

(中北大学机电工程学院，山西 太原 030051)

地磁场具有全天候、全天时、全区域的特点，磁强计具有抗干扰能力强、无积累误差、成本低、抗冲击机性强的优点，使得地磁导航姿态测量技术得到了广泛的应用。但是地磁信号非常微弱，安装在载体内部的磁强计容易受到固定磁场、感应磁场和随机磁场等干扰，从而导致载体姿态测量精度大幅度下降，因此需要对各种干扰磁场进行补偿[1-2]。

目前，国内外学者研究磁场信号去噪的方法主要有傅里叶变换、小波分析、独立分量法以及基于信号时域分析的形态滤波法等，单志超根据铁磁性目标信号的噪声特性和时频特性，提出了一种基于小波变换的磁异常信号背景噪声消除方法[3]。Mandrikova采用小波阈值法和平稳小波变换抑制噪声，提高了地磁异常信号的分辨率[4]。李季采用形态滤波器对磁场信号进行处理，有效地消除了信号中含有的强脉冲干扰[5]。除了这些方法，经验模态分解EMD(Empirical Mode Decomposition)和Hilbert-Huang变换在信号处理领域应用较为广泛，它是一种对非线性和非平稳信号自适应分解的处理方法和时频幅分析方法，但是使用这种方法会出现模态混叠、端点效应等问题，为了改进这些问题，很多学者提出了许多改进算法，如集合经验模态分解(EEMD)、完备总体经验模态分解(CEEMD)和完整集成经验模态分解(CEEDMAN)[6-7]。

本文在分析磁场误差模型的基础上，借鉴EMD阈值设置方式和小波软阈值方法，将CEEMDAN阈值滤波方法应用于磁场信号的去噪中，对含噪声的地磁信号进行完备分解，并将经过阈值滤波处理后的信号与有效信号重构，得到去噪后的信号，通过对实际磁场信号进行分析验证了该方法的有效性。

1 CEEMDAN方法

CEEMDAN根据信号特性自适应地向其添加不同的高斯白噪声，通过计算的残余信号来获取下一级的IMF分量，将含噪信号从高频到低频依次分解出一组IMF分量，可有效解决使用EMD出现的模态混叠问题并提升分解过程的完备性及分解效率[8]。

首先定义一个运算符Ej(·)，表示为采用EMD产生的第j个IMF，ωi(n)为N(0，1)的白噪声，εi为白噪声的幅值系数，x(n)为原始数据，CEEMDAN算法的步骤如下:

①首先向原始信号x(n)中添加白噪声ε0ωi(n)，获得信号Xi(n)为:

式中:i为加入高斯白噪声的次数i＝1，2，…，N。先求取第一阶IMF分量IMF1，对于第i次加入白噪声的Xi(n)，进行EMD分解，得到IMFi1，重复计算N次，对其集成平均可得到第一阶IMF为:

由原始信号x(n)和第一阶IMF获取一阶残差为:

②在一阶残差r1(n)的基础上添加白噪声ε1ωi(n)，获得信号r1(n)＋ε1ωi(n)，同样进行EMD分解，得到IMFi2，重复计算N次，对其集成平均可得到第二阶IMF为:

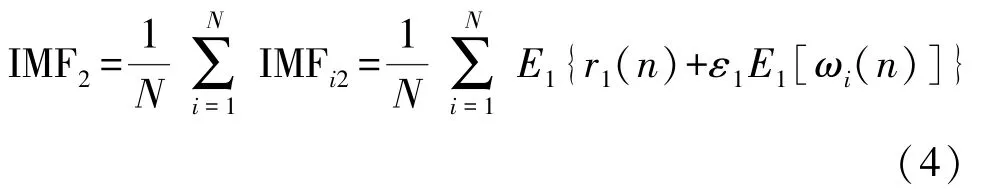
由一阶残差r1(n)和第二阶IMF获取二阶残差为:

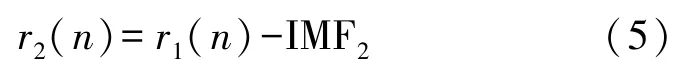
③在残差rk-1(n)的基础上添加白噪声εk-1ωi(n)，获得信号rk-1(n)＋εk-1ωi(n)，进行EMD分解，得到IMFik，重复计算N次，则k阶IMF为:

分解得到k阶残差为:

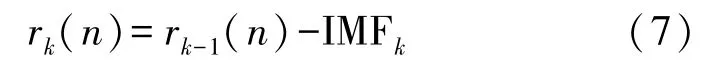
④返回步骤③继续进行下一步分解，直到残差不能分解为止，最终残差为R(n)；

⑤获得最终分解结果，原始信号x(n)可以表示为:

最终信号通过CEEMDAN分解后得到一系列从高频到低频的IMF分量，CEEMDAN利用噪声自适应的特点，可对原始信号进行精确完整的重构。

2 CEEMDAN阈值滤波去噪模型

2.1 磁场误差模型的建立

使用双轴磁强计测量弹体滚转角过程中，有很多磁场干扰源，根据其表现形式的不同可以分为固定干扰磁场、感应干扰磁场、随机干扰磁场等[9]。

固定干扰磁场是指弹体上硬磁性材料产生的磁场，其磁性在一定时间内不随外界磁场的变化而变化，因此固定磁场的磁场强度不变，可表达为:

感应干扰磁场是指软磁性材料在地磁场的作用下产生的磁场，其磁性随外界磁场的变化而变化，呈现一定的比例关系，可表达为:

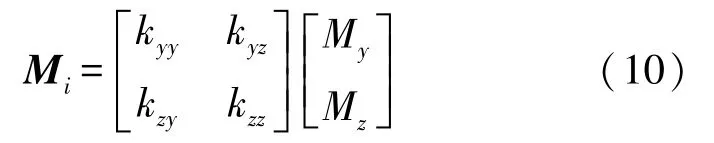
磁强计的制造误差包括零位误差、灵敏度误差和非正交误差，其系数分别为零位误差系数Bo、灵敏度误差系数Cl和非正交误差系数Cn，大小不随磁场的变化而变化。

随机磁场的来源复杂，频谱范围宽，主要包括电路系统内电子元器件内部产生的热噪声、散粒噪声和量子噪声，可认为其为白噪声，还有舵机产生的影响，舵机由电机驱动，在工作的瞬间会产生瞬时强磁场脉冲，工作过程中，舵翼转动的频率大小也会产生不同频率的噪声，随机干扰磁场用ωt表示。

设真实磁场信号为M，则磁强计输出的误差模型为:

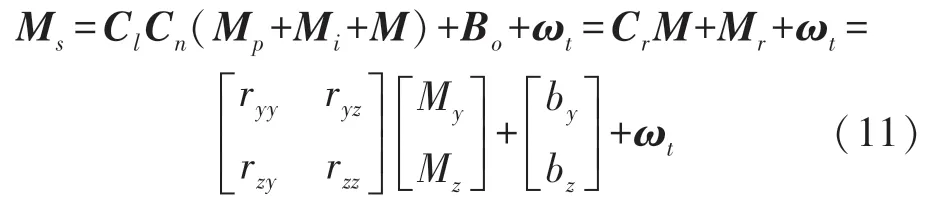
根据地磁场理论，在某一空间内地磁场的磁场强度矢量M的标量大小为恒定值，设为M0，所以当不考虑噪声影响时，弹体在这一空间内做任意姿态运动时，双轴磁强计所测得的磁场分量满足:

从上式可以看出，不考虑噪声影响时，随着弹体的姿态角运动，矢量M顶点的轨迹是一个圆心在原点，半径为M的地磁圆[10]。在固定磁场干扰、感应磁场干扰、自身误差和随机误差的影响下，由磁强计误差模型Ms＝CrM＋Mr＋ωt可知，双轴磁强计所测数据的轨迹在几何上可解释为经过伸缩、旋转、平移畸变为斜椭圆，由于随机误差不能用固定的参数进行表示，导致斜椭圆模型的固定干扰系数、感应干扰系数、零位误差系数、灵敏度系数、非正交系数等不能准确地估计，所以需要提前将磁场信号进行滤波处理，滤除随机干扰，然后进行斜椭圆拟合参数估计，可得到斜椭圆模型如式(13)所示:

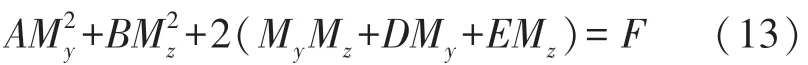
2.2 利用自相关系数和傅里叶变换确定分界点

采用CEEMDAN方法对含随机噪声的磁场信号进行完备分解后，得到主成分为噪声的IMF、有效地磁信号与噪声混叠的IMF和有效地磁信号IMF，为了将包含噪声的IMF分量中的噪声信号滤除，和剩下的有效信号IMF分量进行重构来实现信号的降噪。因此需要准确地找到噪声IMF分量与有用信号的IMF分量之间的分界，它直接决定CEEMDAN滤波方法的降噪效果。

文中利用噪声的数学特性来寻找分割点，自相关函数是描述信号变化的剧烈程度的函数，也反映了同一个信号在不同时刻间的相关程度。由图1可看出，对于理想高斯白噪声信号，由于数据在各个时间点的随机性，在不同时刻两个信号之间的关联性很差，所以随机噪声的自相关系数在零处取得最大值，在其他点处趋近于零[11]。

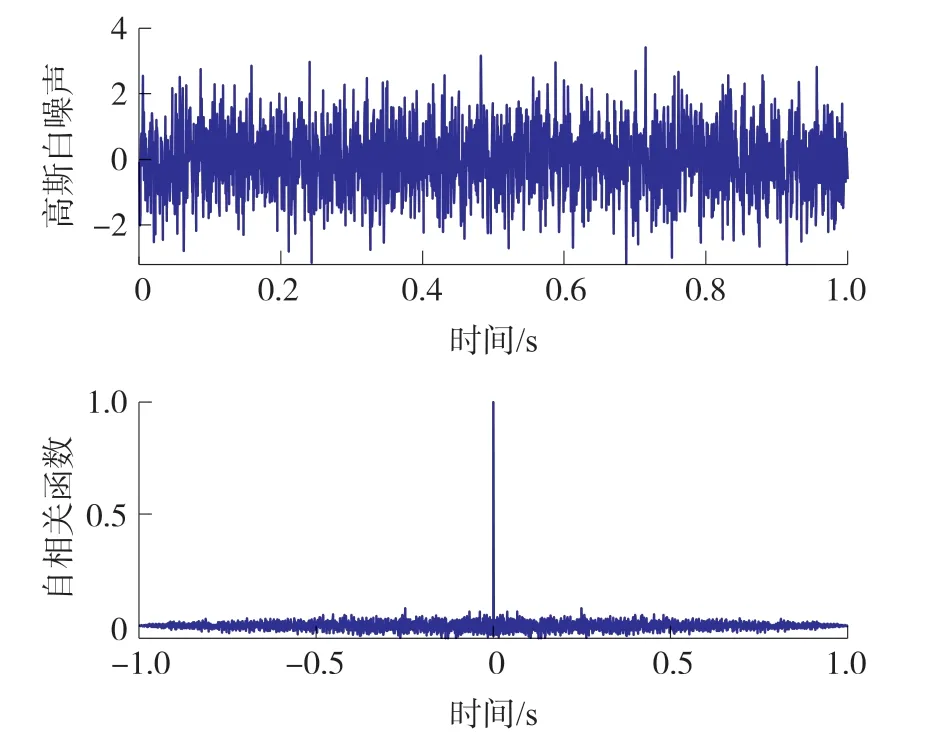
图1 随机信号与其归一化自相关函数

分析图2的正弦函数归一化自相关函数，可观察到自相关系数也是在零处取得最大值，但是由于正弦信号在不同时刻的数据存在着相关性，因此在其他点处自相关系数是随着时间差的变化而变化的，没有立即减小到零。

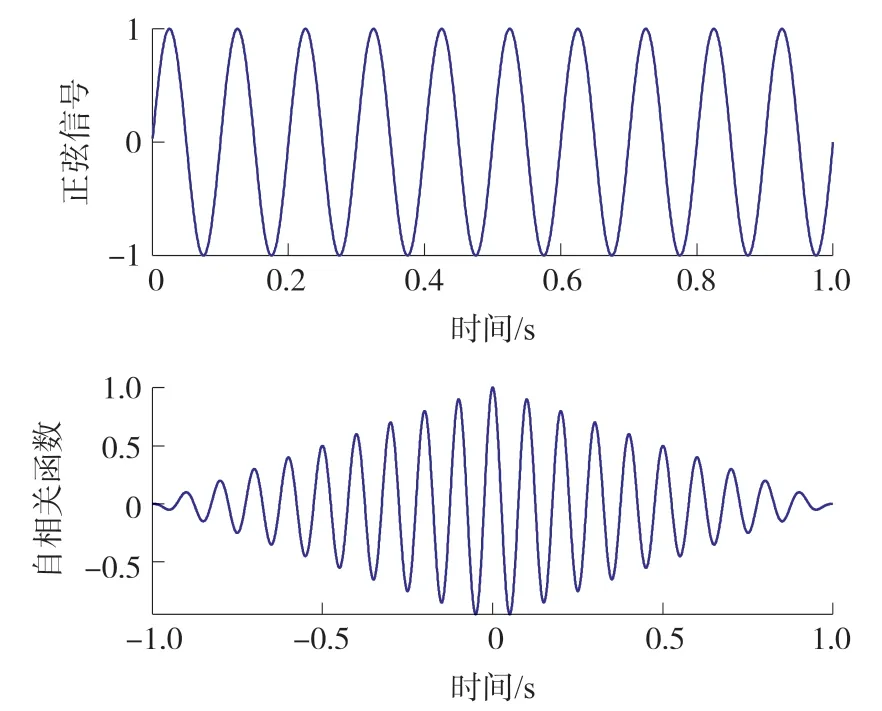
图2 正弦信号与其归一化自相关函数

已知原始信号为x(t)，其自相关函数表达式为(14):

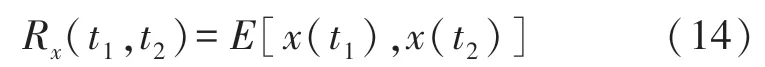
采用归一化自相关函数计算噪声与信号模态分量的自相关函数值，归一化函数的表达式为式(15):

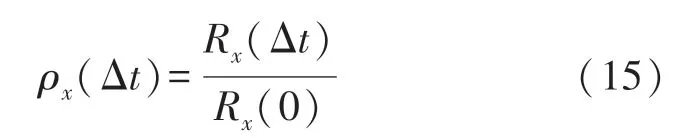
对含有随机噪声的地磁信号进行CEEMDAN分解得到IMF分量，可以根据上述特点来根系各个IMF的自相关函数，进而判断出含噪声的IMF分量和有效信号IMF之间的界限[11]。但是由于噪声的复杂性，自相关函数曲线的不确定性，可以对各个IMF分量进行傅里叶分析，从频域对信号进行分析，根据地磁信号的低频特性来进一步确定分界点。

2.3 小波阈值去噪算法

由于一般信号在时间域上的连续性，而随机噪声在时间域上是不连续性的，因此在小波域，有效信号所产生的小波系数其模值较大；而高斯白噪声经过小波变换，在小波阈仍然表现为很强的随机性，其对应的系数很小。根据该特点，需要通过设置阈值函数进行去噪处理，大于阈值的系数保留下来，而小于阈值的分解系数则通过置零进行消除[12]。

CEEMDAN通过添加有限次的自适应白噪声来减少重构误差，但是经过分解得到的高频IMF分量可能中含有有效分量信号，因此本文根据EMD阈值的设置方法，采用小波软阈值的处理方式，将高频IMF进行阈值处理后，对其滤波后的分量与有用分量进行重构以达到信号去噪的目的[13]。

对前(k-1)个IMF噪声分量使用阈值滤波，阈值处理形式采用软阈值的方法，表达式为:

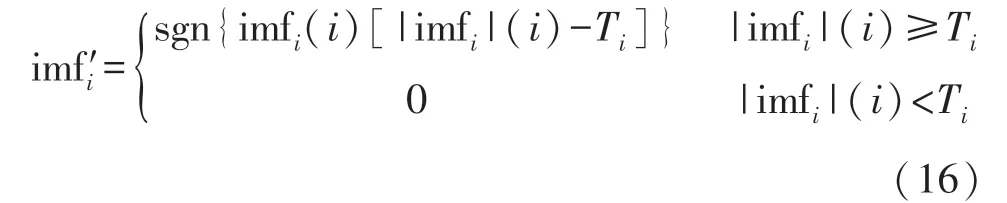
式中:imf′i为去噪后的第i阶IMF分量，Ti为第i阶IMF分量的阈值。阈值确定的方法采用EMD方法中的阈值计算模型:

式中:σ唯一常数，Ei为第i阶IMF对应的能量，其值可以使用式(18)进行估计:

对前k阶IMF进行小波软阈值处理之后，得到前k阶滤波后的IMF分量为IMF′，和k阶后的IMF分量可得到重构后的信号为:

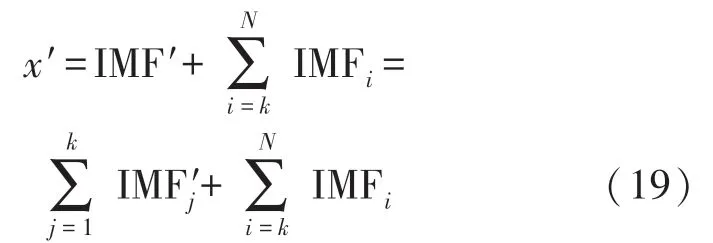
2.4 去噪效果评价指标

为了分析CEEMDAN阈值滤波算法的降噪效果，本文采用均方根误差和信噪比指标对地磁信号的去噪效果进行评价。

均方根误差表示的是真实信号与重构信号偏差大小的一个指标，均方根误差越小，表示去噪后的信号与真实信号之间的偏差越小[14]，其表达式为:

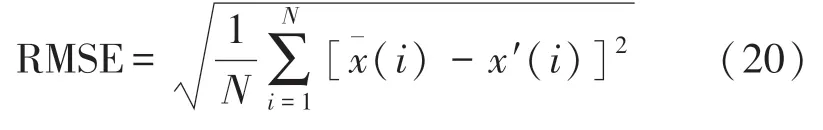
信噪比为有用信号功率与噪声功率的比值，表示的是信号中的有效成分与噪声成分的比例关系，信噪比越大，表示信号中噪声所占的比例越小，其表达式为:

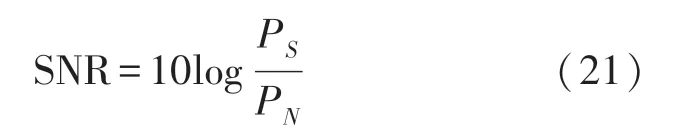
式中:PS为有用信号的功率，PN为噪声的功率。

3 实例分析

实验中采用双轴磁强计，弹体上的电子设备及供电系统和执行机构工作的时候会产生预期范围内的高频干扰噪声。为了验证CEEMDAN滤波算法在地磁测量信号中的滤波效果，首先，只给地磁组件供电，将装有磁强计的弹体放在无磁转台上，以1.5 Hz的频率匀速转动，磁强计输出的模拟信号经过16AD转换后经过DSP以50 Hz的采样频率进行采集，得到无外界干扰的磁场信号，然后地磁组件和其他组件一起供电，在旋转的过程中电机以10 Hz的频率开始工作，可得到包含噪声的磁场信号，以采集到的Y轴的信号Ny为例，如图3所示。

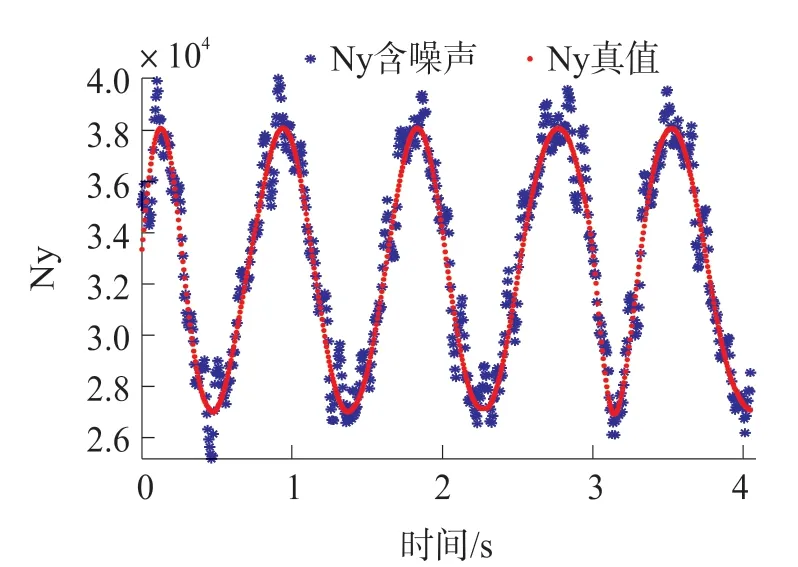
图3 原始磁场信号与含随机噪声的磁场信号

文中将采集到的无外界干扰的磁场信号作为真值，使用CEEMDAN阈值滤波去噪方法对包含噪声的磁场信号进行处理后与真值进行比较。

首先使用CEEMDAN方法对采集到的磁场信号Ny进行分解，其中参数设置如下:噪声标准差为0.2，集成平均次数为500，允许的最大迭代次数为500。Ny经过分解后得到11个IMF分量和一个残余分量，其中分量IMF5~IMF11和余项12如图4所示，通过图4可以观察到经分解后的IMF分量从第八阶IMF分量开始幅值的数量级发生了变化。

图4 含随机噪声的磁场信号经CEEMDAN分解得到IMF5~IMF11与余项

然后根据Ny分解得到的各阶IMF的自相关系数来判断含噪声的IMF分量和有效信号IMF分量之间的分界点，其中第1阶IMF到12阶IMF的自相关系数如图5所示:

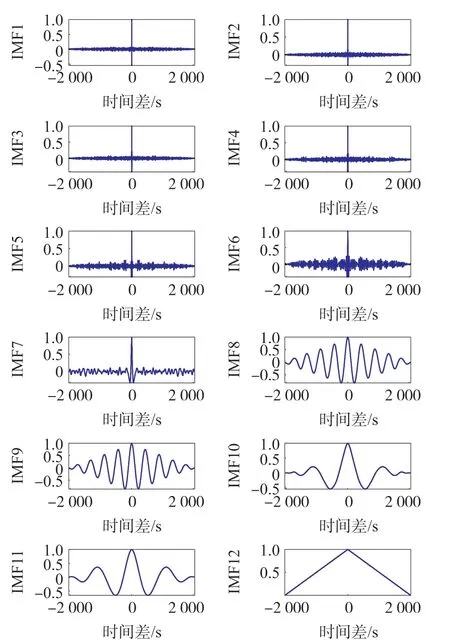
图5 IMF5~IMF11与余项的自相关系数

从图5中可以看出Ny的IMF分量的前七阶IMF的自相关系数和高斯白噪声信号的自相关系数的特点类似，从第八阶开始自相关函数的曲线的特点为零点处最大，在其他点随着时间差的变化而变化，和一般信号的自相关函数相似，由此可以估计分界点为第八阶。再观察第5阶到第八阶各阶IMF的傅里叶变换，如图6所示，从图5中可以观察到第八阶IMF分量的频率集中在1.5 Hz，和转台转动的频率接近，根据地磁信号属于低频信号，其频率值一般在1 Hz以下，由此可以确定含有噪声的IMF分量和有效信号IMF分量之间的分界点为第八阶IMF。

图6 IMF5~IMF8阶的频谱分析结果

然后分别对磁场信号Ny的前八阶IMF分量进行小波软阈值处理得到IMF′，根据式(22)

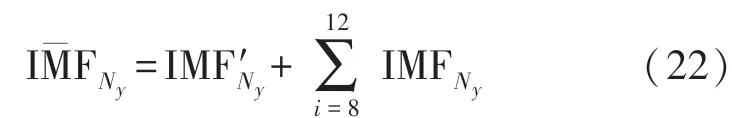
得到重构信号和真实信号如图7所示。

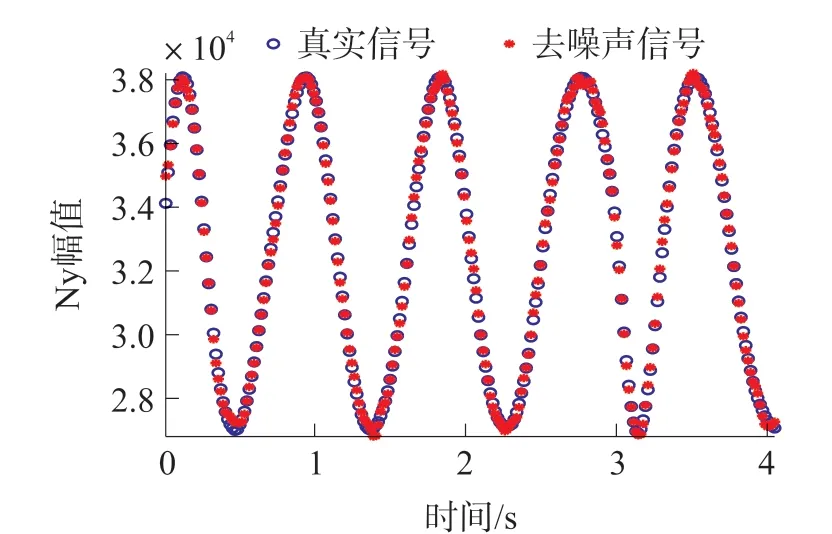
图7 原始地磁信号与重构地磁信号

最后为了验证该算法的可行性，本文分别采用了使用CEEMDAN强制滤波和本文提出的CEEMDAN阈值滤波算法处理磁场信号进行比较，通过表1可以发现分别信噪比提高了1.156 dB，均方根误差提升了10.52%，如表1所示。

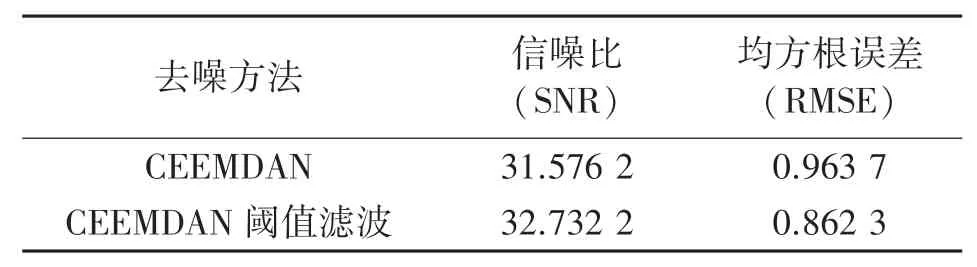
表1 去噪精度指标

将经过CEEMDAN小波阈值滤波得到的重构信号Ny、Nz根据磁场误差模型，建立斜椭圆模型，得到由真实数据、含噪数据和重构数据得到的斜椭圆分别如图8所示:

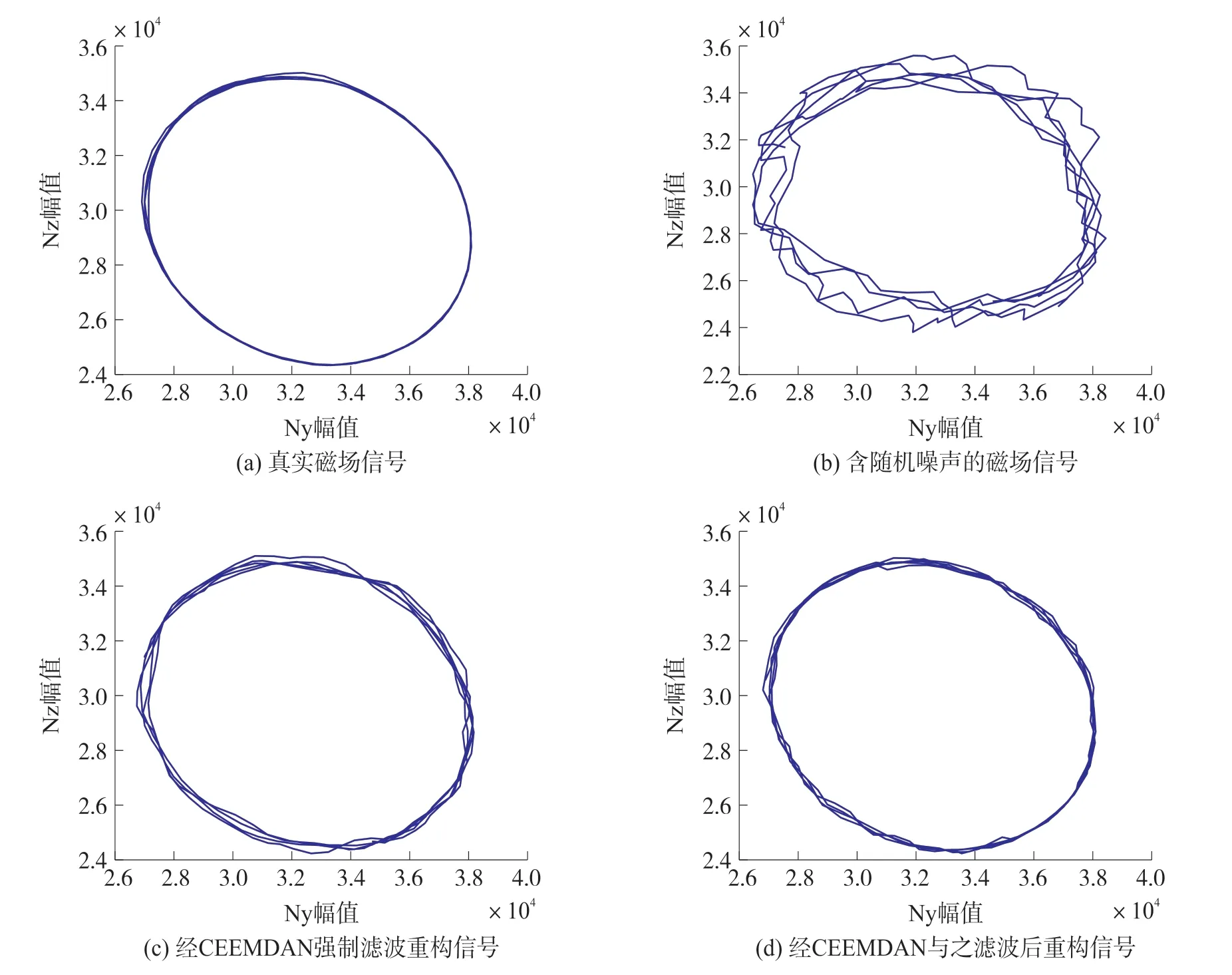
图8 不同信号构成斜椭圆

磁场误差补偿的效果可以用重构后的信号构成的椭圆距真实磁场数据构成的椭圆的几何距离L来衡量

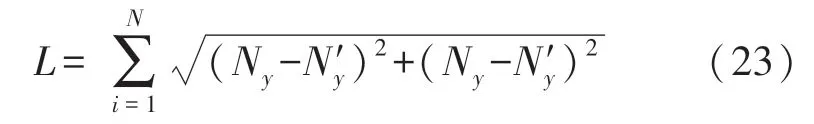
几何距离L越小，说明补偿后的斜椭圆越接近真实斜椭圆，可得到含噪声的磁场数据、经过CEEMDAN强制滤波后的磁场数据和经过CEEMDAN阈值滤波处理后的磁场数据的几何距离，如表2所示，对比CEEMDAN强制滤波，经过CEEMDAN阈值滤波处理后的磁场信号几何距离下降了13.87%，表明了本文所提方法的有效性，可以为椭圆参数估计进行预处理。

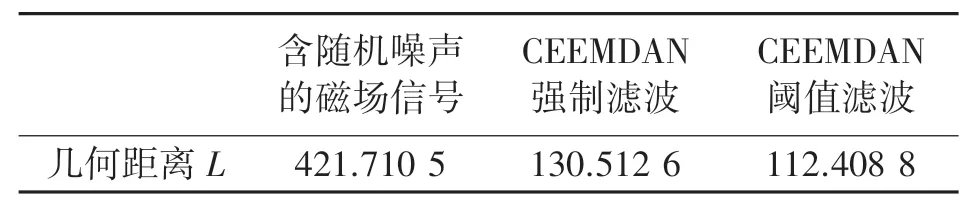
表2 几何距离指标

4 结论

本文针对地磁信号的特点，根据CEEMDAN方法能够对信号进行完备分解的基础上，提出使用自相关系数和傅里叶变换确定IMF分量中噪声IMF分量与有用信号IMF分量之间的界限，借鉴EMD阈值设置方式，结合小波软阈值对含噪声的IMF分量进行滤波处理，最后重构信号以得到去噪后的信号。通过对实际磁强计输出磁信号进行CEEMDAN阈值滤波处理之后分析均方根误差、信噪比和椭圆间的几何距离，结果表明:本文提出的方法要优于CEEMDAN强制去噪方法，验证了该方法在处理含噪声的磁场信号上的可行性和优越性。