基于视觉和轮速计紧耦合的轮式机器人定位算法研究*

朱道俊，徐湛楠，马婷婷，曹平国，宋全军*

(1.中国科学院合肥物质科学研究院，安徽 合肥 230031；2.中国科学技术大学研究生院科学岛分院，安徽 合肥 230026)

随着机器人技术的发展和计算资源能力的提高，轮式机器人的应用逐渐得到普及。定位技术是实现轮式机器人自主导航的重要技术环节。对于室内外小场景范围内的轮式机器人应用，如巡逻机器人，低成本、高精度、高鲁棒性、易用性成为了定位系统的研究目标。

同时建图与定位(SLAM)技术[1]是研究机器人在未知环境下定位的主流技术方案。其中基于视觉传感器的SLAM(V-SLAM)技术由于其低成本、测量信息丰富得到了广泛研究。经典的VSLAM工作有PTAM[2]、ORB-SLAM[3]、ORB-SLAM2[4]等，Mur-Artal R等提出的ORB-SLAM第一次将SLAM分为三个运行线程进行处理，实现了V-SLAM大场景下的实时运行能力[3]。然而实际环境中由于场景特征的单一(如走廊环境)和传感器的快速运动等，很容易导致V-SLAM定位失败，鲁棒性较差。

视觉-惯性融合SLAM(VI-SLAM)是通过融合视觉和IMU传感器的SLAM方案，由于IMU具有很好的动态特性，VI-SLAM能有效处理机体的快速运动和场景单一的情况。经典工作有MSCKF[5]、SMSCKF[6]、OKVIS[7]、VINS-Mono[8]等。香港科技大学秦通等提出的VINS-Mono因其快速精确初始化流程、视觉-惯性紧耦合非线性滑动窗口优化估计器、四自由度位姿图优化等特点成为当前VI-SLAM中定位效果最好的算法之一，实现了在无人航空飞行器上的精准位姿轨迹估计，然而其在轮式移动机器人上的应用却会出现很多退化问题，导致定位精度下降甚至定位失败。为了实现VINS-Mono精确有效的初始化，需要保证初始化过程中机体有充分的三轴运动激励，而轮式机器人由于平面运动的限制，很难做到这点。Wu等通过数学和实验证明了当轮式机器人在某些特定运动场景下，VINS会出现额外的不可观自由度，会带来很大的估计偏差[9]，比如纯直线运动、常量局部加速度运动等，而这些运动情形在轮式机器人上是很常见的。

针对轮式机器人，轮速计传感器可以很好的替代IMU，轮速计也能够提供高频率的机体状态量测量，同时对于特殊运动场景，轮速计不会带来退化问题。Wu等也证明了通过融合轮速计信息能够避免尺度不可观的问题，提高定位精度[9]。Zhang等[10]、Liu等[11]、Lee等[12]通过融合视觉-IMU-轮速计信息来实现轮式机器人定位，结果相比于VINS都有了很大的提高。Zheng等提出了一种基于视觉-轮速计紧耦合的定位系统，它基于ORB-SLAM框架进行改进实现，提出了一种新的视觉重投影观测误差形式[13]。

为了同时追求系统的运行效率和定位精度，本文发现在室内外小范围平面运动场景下，视觉-IMU-轮速计定位系统相比于视觉-轮速计定位系统，会引入大量的额外系统负担，比如，IMU的融合大大增加了系统的状态维度、增加了系统初始化的难度[8]，然而定位精度不会有很大的提高，甚至对于低成本IMU，会带来更大的定位误差。因此，本文中提出紧耦合视觉和轮速计定位方案，提高系统定位精度的同时提升系统运行效率，主要贡献如下:①提出了一种基于非线性滑动窗口优化的视觉-轮速计定位系统估计器；②提出改进了一种联合视觉-轮速计的快速精确系统初始化方案。③轮速计-相机坐标系变换外参在线标定。

1 数学记号

在本文中，我们使用大写字母表示向量/矩阵，使用小写字母表示标量，∈SO(3)表示坐标系B到坐标系A的旋转变换，为其单位四元数表示，这里使用Hamilton表达形式[14]；ApB∈R表示坐标系B原点在坐标系A下的坐标；A(·)表示坐标系A下的某量，表示状态估计值或者测量值，δ(·)表示状态的误差形式，本文使用右乘扰动来定义旋转误差，其形式为:

⊗表示四元数乘法，(·)img表示四元数的虚数部分；表示向量对应的反对称矩阵，比如向量a＝[a1a2a3]T对应的反对称矩阵为:

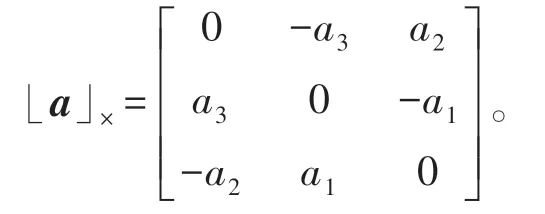
ei表示R3×3单位矩阵的第i列，。SO(3)上的李代数表示为so(3)，log(·)获得SO(3)对应的so(3)，反之，exp(·)将so(3)转换为SO(3)。向量v的第i个元素表示为v(i)。

本文涉及到三个不同的坐标系，分别是世界坐标系、轮速计坐标系(机体坐标系)和相机坐标系，我们将它们依次表示为w、b和c。另外bk、ck表示时间顺序上第k个机体坐标系和对应的相机坐标系。

2 系统描述

如图1所示。系统输入为相机和轮速计观测信息，对于新的图像帧，先使用KLT光流法跟踪上一帧的特征点，再提取新的Shi-Tomasi角点。对于新帧和上一帧之间的轮速计测量值，进行预积分处理，详见4.4节。

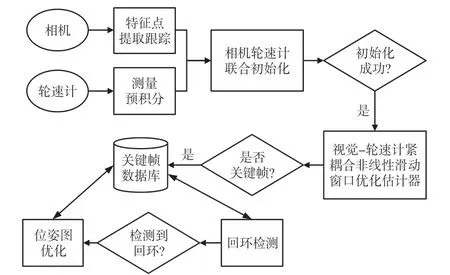
图1 系统流程图

若系统未完成初始化，则进行相机轮速计联合初始化，详见3节。若初始化成功，则进行视觉-轮速计紧耦合非线性滑动窗口优化，详见4节，若窗口中帧数达到最大，则判断次新帧是否为关键帧，若是，则选择窗口中的最老关键帧进行边缘化，否则边缘化次新帧[8]。

为消除长时间累积误差，对新关键帧进行回环检测，在历史关键帧数据库中查找当前关键帧的回环帧。回环检测基于视觉词袋库DBoW2[15]进行实现。若检测到回环，则进行六自由度位姿图优化，保证长时间位姿轨迹估计的一致性[8]。

3 视觉-轮速计联合初始化

与VINS-Mono不同的是，本文提出使用两帧快速初始化，将第一帧F0设置为世界坐标系原点，为保证比较好的初始化，初始化两帧之间需要有足够的视差，设置初始化视差阈值为Tp，当前帧Fc与F0的视差小于Tp时，则丢弃该帧，反之，设置当前帧为初始化第二帧F1。由于轮速计能够提供比较精确的短时间位姿估计，因此可通过轮速计积分测量来预测F1的位姿，如图2所示，对F0和F1跟踪匹配的特征点进行三角化，最后进行一次集束调整(BA)优化，所需最小化的误差函数为:

为求解式(2)，我们采用迭代求解的方式，每次迭代通过求解增量方程Hδx＝b得到更新增量δx，然后更新到当前状态估计值上:，对于平移状态，，对于旋转状态，。本文中使用Ceres Solver库[16]来求解上诉迭代优化问题。

4 视觉-轮速计紧耦合非线性滑动窗口优化估计器

非线性滑动窗口优化估计器中的状态及测量约束关系可用因子图进行表示，如图3所示，其中圆形和椭圆形表示系统优化的状态，方块表示测量误差因子，与方块相连接的连接线表示该测量因子所关联到的状态。优化的状态包括关键帧位姿、轮速计相机外参和特征点位置，详见4.1节。传感器测量约束因子包括特征点重投影误差因子和轮速计预积分测量误差因子，详见4.2和4.3节。为了处理低频视觉信息和高频轮速计信息的融合，本文进行了相邻关键帧间轮速计测量预积分和误差传播，详见4.4节。

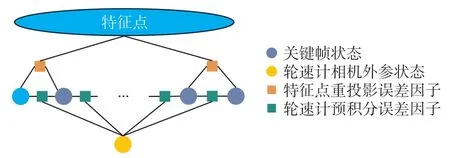
图3 非线性滑动窗口优化估计器因子图

4.1 系统状态

滑动窗口中估计状态为:

式中:N为滑动窗口大小，m为滑动窗口中所能观测到的路标点数量表示第i帧位姿状态，λl，l＝1，…，m表示第l个路标点逆深度状态，参数化表示在锚坐标系(观测首帧相机坐标系)下[8]，定义如下:

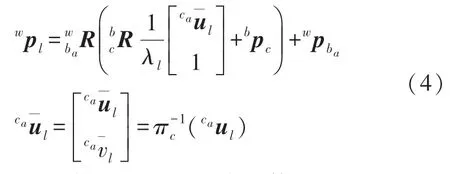
式中:ba/ca分别表示观测首帧机体/相机坐标系，表示路标点l在ca帧下的像素观测坐标值，将其通过相机内参和畸变参数转换到归一化平面坐标，这个转换过程即为。表示轮速计坐标系和相机坐标系之间的外参变换，这里将其作为系统状态进行在线估计，可以减小不精确的外参标定结果对定位精度的影响。如果有比较精确的外参线下标定值，可以将其从系统状态估计中移除。

4.2 视觉观测误差因子

如图4所示，路标点l在cj帧的重投影误差定义为观测坐标和重投影坐标之间的坐标差值，重投影坐标计算方法为首先将路标点l通过其逆深度和观测首帧位姿估计转换到世界坐标系下，再通过cj帧位姿估计投影到cj帧图像平面上，如下所示:

图4 特征点重投影观测误差

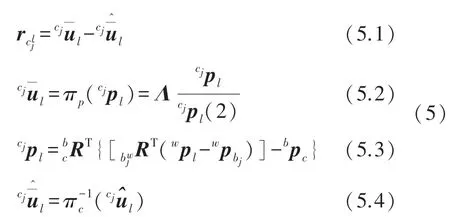
其中式(5.1)表示重投影误差，为路标点l在cj帧上预测归一化平面坐标，为观测归一化平面坐标，式(5.2)将相机坐标系下坐标点投影到相机归一化平面上，为路标点l在相机坐标系cj下的坐标，(2)表示向量的第三个元素，式(5.3)将路标点l的世界坐标转换到cj帧相机坐标系下，通过式(4)计算获得。

由式(4)、式(5)可以看出，路标点l一次视觉重投影误差分别关联到锚机体坐标系位姿状态、当前机体坐标系位姿状态和路标点的逆深度状态，因此需要分别对三个状态求误差雅可比矩阵，分别设为。

4.3 轮速计误差因子

两个相邻关键帧Fk和Fk＋1之间的轮速计积分测量为:

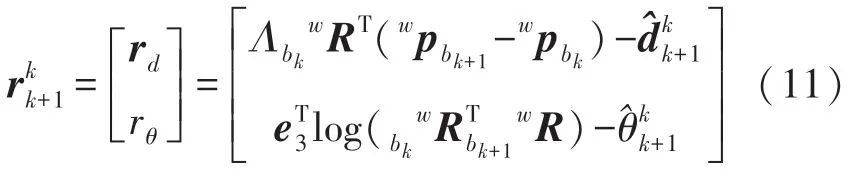
式中:rd表示轮速计平移测量误差，rθ表示轮速计航向角测量误差。

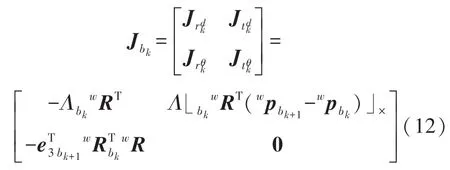
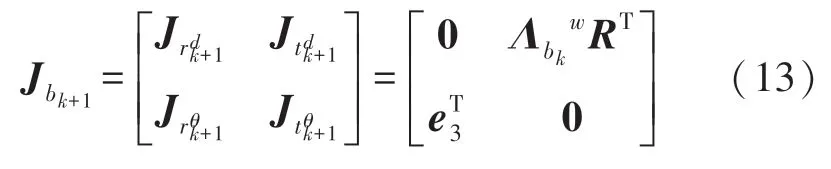
4.4 轮速计预积分

由于相邻关键帧之间有多次轮速计测量，为了获得相邻关键帧之间轮速计测量的噪声协方差矩阵，需要将轮速计测量进行积分。如图5所示，用i、j表示图像测量时间索引，用k表示轮速计测量时间索引，我们将图像测量时刻ti和tj之间的轮速计测量进行积分和误差递推。

图5 轮速计预积分

轮速计k时刻的测量为:

根据SSε(2)上的递推公式，有:

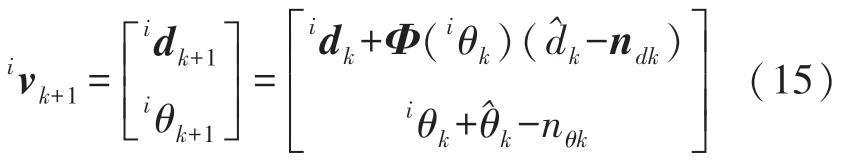
式中:Φ(·)表示对应的二维旋转矩阵，ivk＋1的噪声协方差由ivk噪声协方差和nvk测量噪声协方差递推得到，因此需要求得式(15)对ivk和nvk的雅可比矩阵，设分别为Jvk、Jnk，解析表达式为:

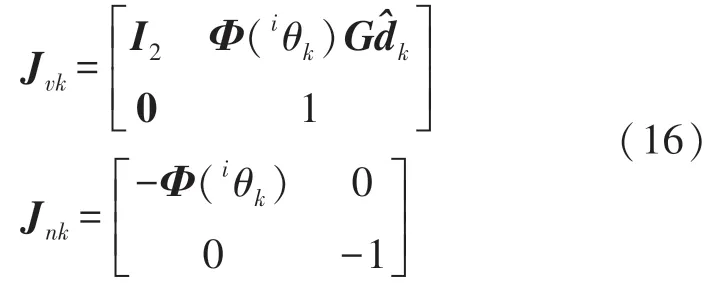
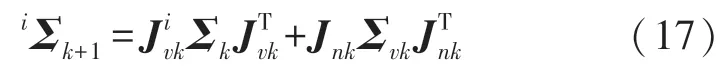
以此递推，可以得到ti和tj时刻图像帧之间的轮速计积分测量ivj和噪声协方差矩阵iΣj。

5 实验及分析

5.1 实验配置

本部分对本文所提出算法进行了实验验证，实验平台如图6所示，四轮车上搭载了一个PC和一个相机。PC用于读取相机和轮速计传感器测量信息和进行算法处理，机器人操作系统(ROS)用来进行四轮车、相机和PC的信息通信传输，使用操作系统为Ubuntu18.0。

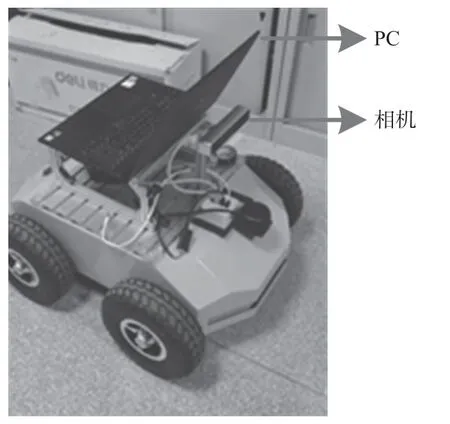
图6 实验平台配置

实验设备的具体型号配置如表1所示。本实验代码基于开源VINS-Mono[17]代码框架修改。

表1 实验设备具体配置信息

为了验证所提算法的精确度，另外进行了两组对比实验，其一是基于视觉-IMU融合的VINS-Mono方案；其二是仅使用轮速计的定位方案。为了量化评估轨迹误差，实验数据采集时确保了起始位置和终止位置相同，通过计算终点、起始点位置估计距离差和轨迹总长度的比例来定义估计误差，如式(18)所示，其中为终止点估计位置，为起始点位姿估计，＾S为轨迹总长度估计。因为起始点设置为世界坐标系原点，所以＝0。

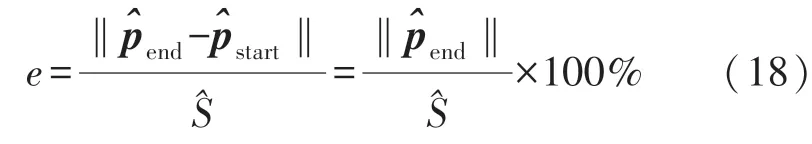
传感器之前的外参数通过线下进行标定，相机内参和相机-IMU外参数通过Kalibr[18]进行标定。相机-轮速计外参数通过CamOdomCalibraTool[19]进行标定，该标定参数为粗略标定，会对该参数进行在线估计优化。

5.2 轨迹误差分析

实验中录制了三种不同场景的数据集进行测试，分别是实验室，会议室和走廊环境，如图7所示。对每个实验场景采集的数据集，分别对本文所提算法和比较算法运行了3次，并取结果平均值作为误差结果。如图8所示，分别为本文所提算法、VINSMono和轮速计在三个实验场景下其中一次运行结果所估计的运动轨迹。从图中可以看出，VINSMono和轮速计都产生了很大的轨迹误差，VINSMono甚至在实验室场景中产生了发散，原因在于以下几个方面，一是本实验采用了低价的IMU传感器，有比较大的误差，二是VINS-Mono对相机和IMU之前的外参标定和时间同步参数有很高的精度要求，而这对低价的传感器配置来说是很难实现，三是本实验的场景主要是平面运动，且大部分是直线运动和匀加速运动，这给VINS-Mono的初始化以及后面的估计带来了很大的不可观问题[9]。另外，仅用轮速计的轨迹估计随着时间增长误差将不断增大，原因是轮速计是通过积分得到位姿估计的，因为测量带有误差，所以长时间的轮速计积分将不断积累误差。而本文所提算法通过融合相机和轮速计信息获得了很精确的定位表现，通过视觉特征点、观测测量来矫正轮速计积分误差，同时轮速计积分测量也对相邻帧间的位姿起到较精确的约束作用。相比IMU，视觉-轮速计融合能够获得更鲁棒的表现，机体终点位置估计能很好的回到初始点，其终点位置估计误差如表2所示。如图9所示为所提算法和其他两种对比算法分别在三种实验场景下的估计轨迹误差，其中水平横轴表示不同的估计算法，水平纵轴表示不同的实验场景，垂直轴表示算法估计误差。可以看出所提算法相比于VINS-Mono和纯轮速计估计都有很大程度的精度提高。

图7 实验数据采集环境，从左至右分别为实验室、会议室和走廊

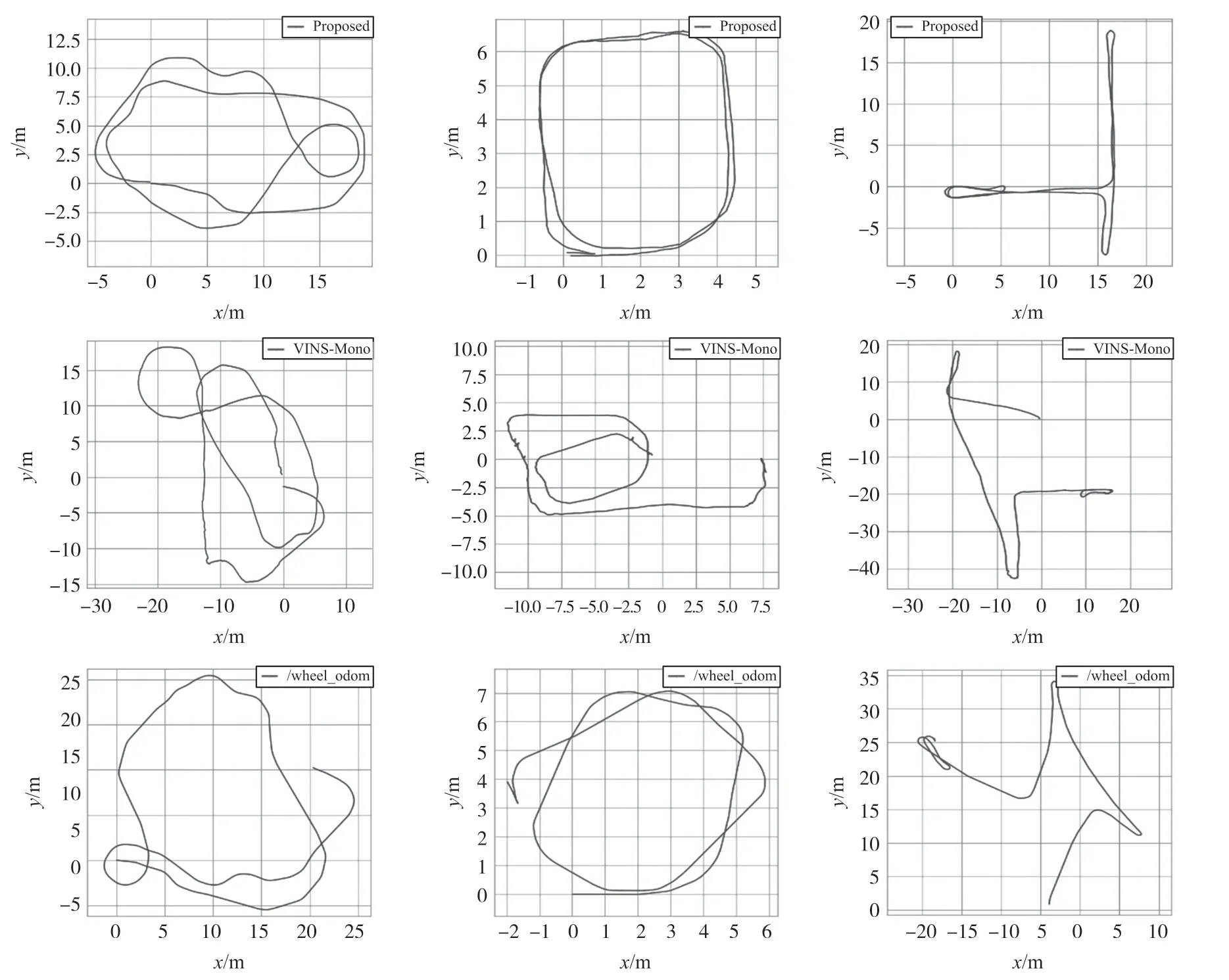
图8 所提算法和其他两种对比算法分别在三种实验场景下的估计轨迹对比图

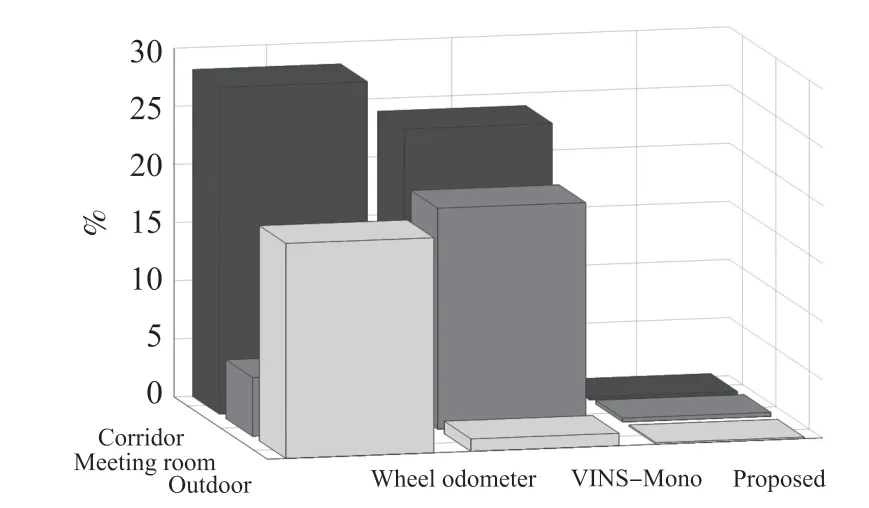
图9 所提算法和对比算法分别在三种场景下估计轨迹误差对比

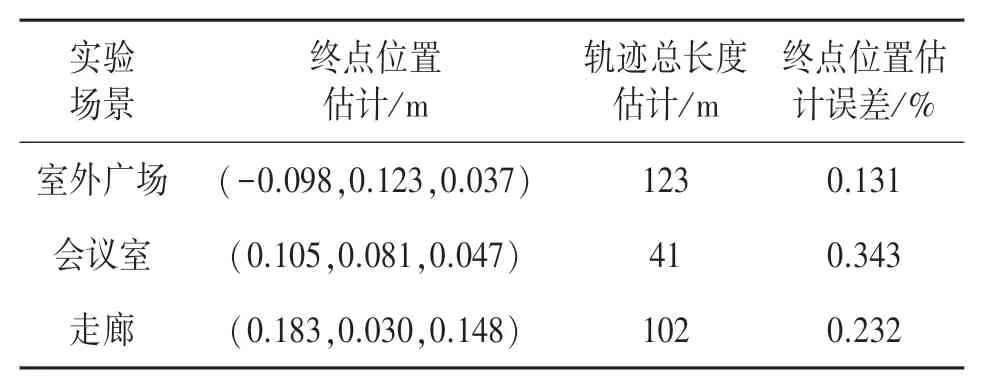
表2 所提算法在三个实验场景下的估计误差

5.3 轮速计-相机外参在线标定实验分析

实验中对轮速计-相机外参进行了粗略线下标定，为了进一步优化该参数，可对其进行在线估计。轮速计-相机外参数有6个自由度，分别是3自由度平移和3自由度旋转，然而由于平面运动，只有5个自由度可观，z轴平移不可观[20]，因此只能估计出轮速计-相机外参数中的x、y轴平移和roll、pitch、yaw旋转角。如图10和图11所示，分别为轮速计-相机平移外参和旋转外参估计值，可以看出，参数估计在经历初始阶段的稍微震荡后，最后都趋于收敛稳定。

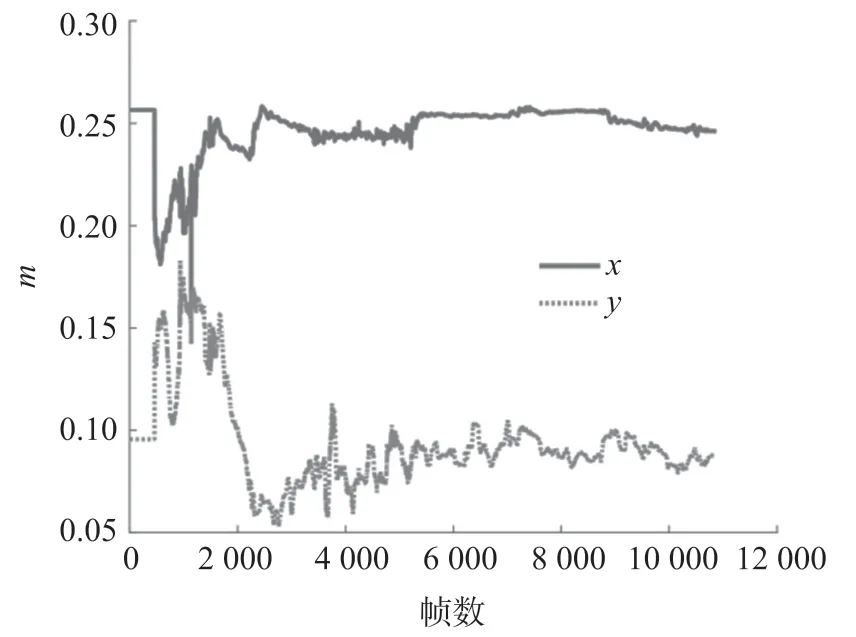
图10 轮速计-相机平移外参在线估计结果

图11 轮速计-相机旋转外参在线估计结果

5.4 系统运行效率实验分析

本部分实验对比了所提算法与VINS-Mono的运行效率。保持其他条件参数相同，如滑动窗口大小(实验中设置为10帧)，优化完成的最长时间(实验中设置为0.04 s)和最大迭代次数(实验中设置为8)。以会议室场景为例，如图12所示，为两个系统在初始化完成后的30 s内每次迭代优化所需的时

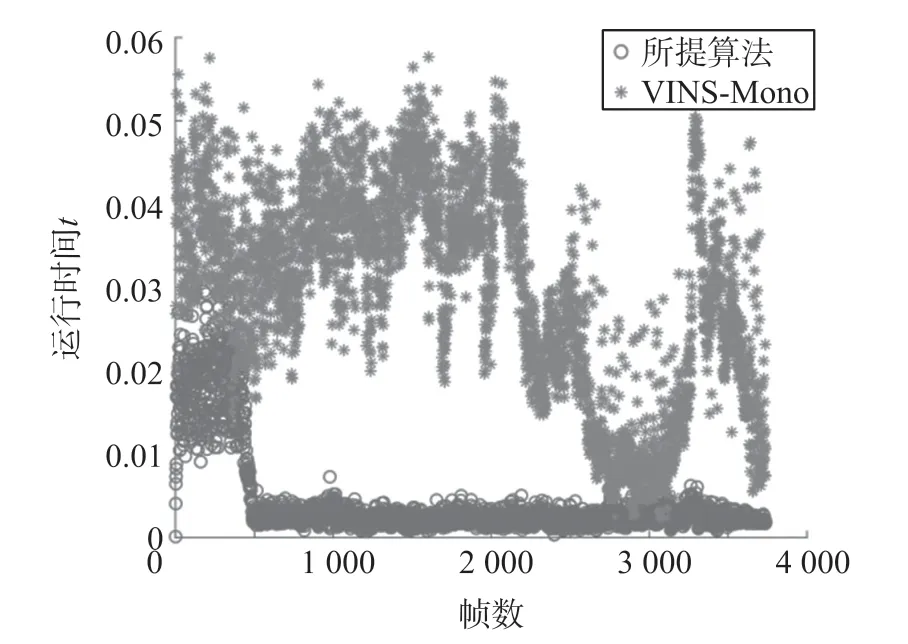
图12 本文所提算法与VINS-Mono运行效率对比

间，可以看出本文所提算法一次优化耗时大约是VINS-Mono的1/10，效率得到了很大提高。原因在于轮速计信息的融合并没有引入额外的系统状态，每帧的状态维度为6维，相反，VINS-Mono系统中，每帧需要估计的状态维度为15维，因此大大增加了优化迭代时需要的时间。

6 结论

本文提出了一个基于视觉-轮速计紧耦合的轮式移动机器人定位算法。采用了基于滑动窗口的非线性优化框架，最小化特征点观测重投影误差和帧间轮速计积分测量误差，来保证系统的实时性和精确度。此外，本文提出了基于视觉-轮速计联合的系统初始化流程，能够快速精确的完成初始化。本文所提系统中对相机-轮速计坐标系变换外参进行了在线标定，在粗略的线下标定外参数下，对其进行在线估计优化，减少了对传感器线下高精度标定的要求。通过实验表明，在低成本实验传感器配置的情况下，本文所提算法在小范围室内外轮式机器人应用场景下相比于VINS-Mono获得了更鲁棒更精确的定位表现，同时运行效率也有比较大的提高。本文实验场景为室内外规则平面环境，未考虑轮速计打滑造成的影响，下一步将加入对轮速计打滑情况的处理。