基于遗传算法的频谱作曲技术研究

苏飞

(商洛学院 艺术学院， 陕西 商洛 726000)

0 引言

近些年来，在频谱作曲中，将计算机技术应用于乐谱研究成为一个重要的研究方向。通过某种算法策略控制获得音符序列，最终得到完整旋律，形成一种算法的频谱作曲，能向观众传递直观感受，因此，频谱作曲相较传统作曲方式实用性更高[1-2]。在计算机作曲方面，目前已经有多种计算机算法应用于频谱作曲中，如应用较多的神经网络算法、专家系统法、马尔科夫链表转换法等[3-6]。但算法在应用过程中存在一定局限性，神经网络算法对采用的数据提出了较高的要求[7]，而专家系统更多的受限于谱曲的规则限制[8]，马尔科夫链表转换法更多的是依靠当前所具备的知识和信息来实现对音乐频谱作曲[9]。相较而言，遗传算法不依赖于问题参数本身，能够获得更好的全局最优解特性，被越来越多地应用于乐曲创作中[10]。通过利用遗传算法对乐曲进行编码，并采用交叉、变异算子获得满意解能较好的保证乐曲的呈现度[11]，但利用遗传算法在进行频谱作曲时，容易忽视短句的构成或调性更高的音乐频谱，适应函数主要依靠系统本身定义，使得乐曲差异性较大[12]。基于此，本研究提出一种新的音乐知识遗传算法，通过在适应函数中引入人的策略来提升评价标准，有效提升遗传算法在频谱作曲中的适应度和呈现度。

1 遗传算法的频谱分析

1.1 算法的基本流程

遗传算法(GA)基于自然选择和遗传变异的全局概率算法，形式简单，具有较强的普适性。通过遗传算法来采用二进制编码方式，能减少外界噪声对乐谱的影响，将乐谱信息方便地表示出来[13]。遗传算法的谱曲流程，如图1所示。

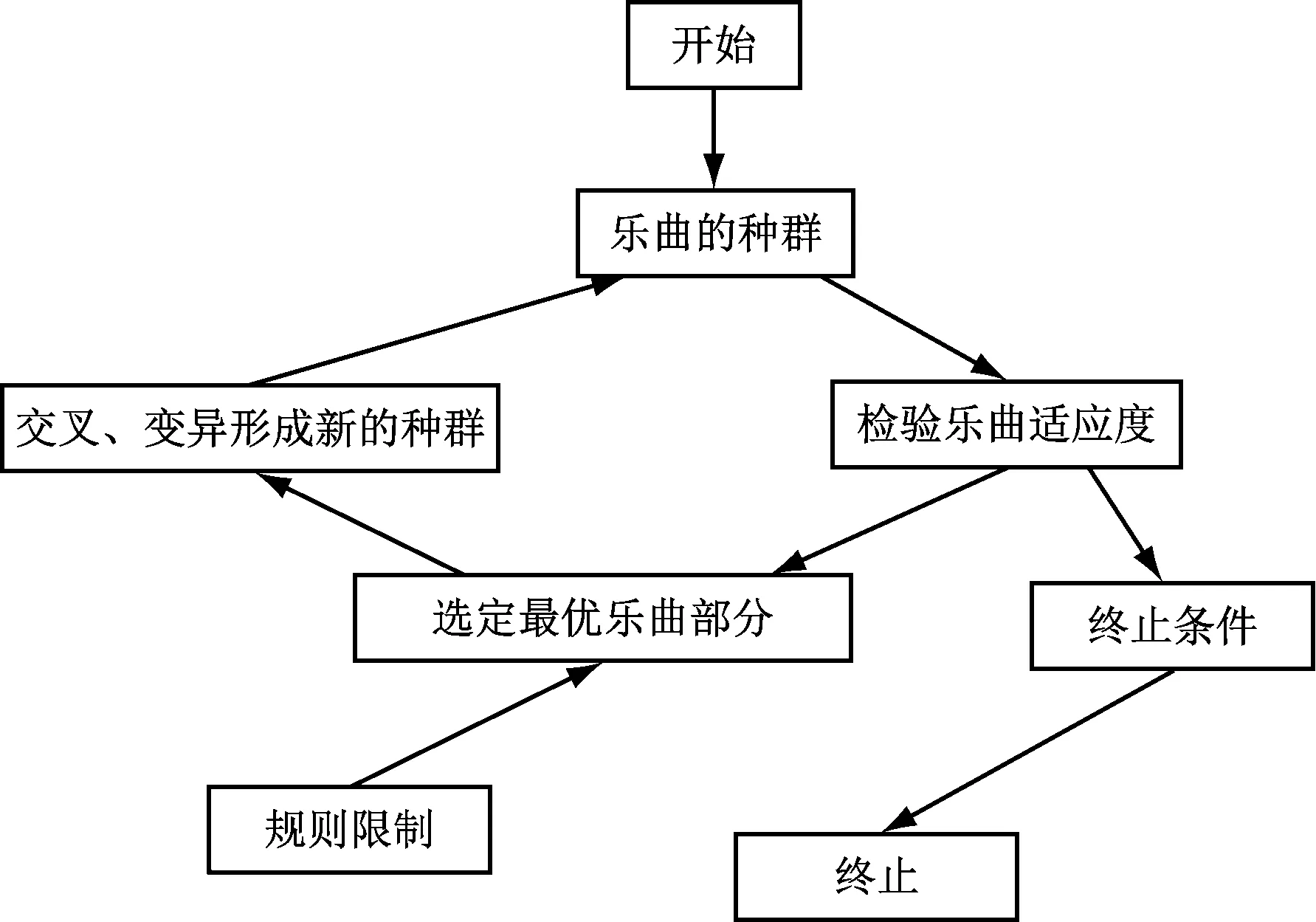
图1 遗传算法的编曲流程

算法的具体流程如下。

(1) 选择编码策略，将乐曲集合X转化为串结构空间S；

(2) 定义适应度函数f(x)；

(3) 根据进化策略选择群体n，确定交叉、变异算法，交叉概率Pc、变异概率Pm等参数；

(4) 生成初始化群体P；

(5) 计算群体串解码后的适应度函数f(x)；

(6) 通过交叉、变异算子形成新一代群体；

(7) 判定群体是否满足规则限制，或算法达到迭代次数，若不满足则返回步骤(6)重新计算。

1.2 算法的编码策略

遗传算法编码是将一个问题的可行解从解空间域转化为能处理的搜索空间中，描述问题可行解的过程。编码决定了染色体排列形式，同时决定了基因变换到解空间的表现形式和交叉、变异操作[14]。通常，遗传算法作曲时，采用二进制编码方式将乐谱信息表示出来。

1.3 算法的适应度函数

在遗传算法的作曲过程中，首先要制定相关规则用编码的形式将音乐知识表现出来，再根据交叉、变异后获得新的乐曲，作出评价。通常适应度函数根据不同乐曲间要素差异，定义权值获得不同适应值[15]。乐曲的要素如下所述。

(1) 大的间隔度：遗传算法中进行交叉、变异算法的初始染色体是随机的，因而乐曲中的连续音符间存在较大间隔。为避免这类间隔造成乐曲频谱杂乱，使用者要限制音符间的最大音程，当音程超过设定值后，适应度阀值取超出部分与权值之积。

(2) 模式匹配：算法执行过程中，在音乐片段间设置匹配模式，从心理学角度将模式匹配加入适应度函数中，听众在欣赏音乐的过程中不仅能识别该模式，同时也希望音乐中展现相类似的音乐模式，此外，音乐中主题的发展也是通过重复的节拍联系起来。

(3) 音符特征：在一个小节中，第一强拍和次强拍作为强拍位置音符，若第一次强拍和次强拍为和音或休止符，则赋予正的权值，若不是和音，则赋予负的权值。对于乐曲中的长音符，使用者可以指定为长音符，对于音符中的长音符，设定和音音符与协调旋流音权值为正，无和音的休止符、音阶音符取负的权值。

(4) 速度：使用者按照一定的标准选定乐曲进行速度，算法通过在每对连续小节中增加音符和休止符判定乐曲的速度。

1.4 算法基本操作

选取曲谱的初始种群后，对编码进行交叉、变异操作，获得新的曲谱，具体操作流程如图2所示。

图2 染色体交叉、变异操作

首先对选择的初始种群染色体进行单点或多点交叉操作，其中适应度更大染色体进入下一轮种群，在作曲系统中，通过变异算子寻找乐曲缺陷或能引人愉悦的乐曲进化方向[16]。对于其中的单个音符变异，随机选定一个音符，并用新的音符代替，或采用稍高的音符，也可随机选取两个音符数量相等片段进行位置交换，或改变染色体的序列，获得新的音符染色体序列。在复制和交叉过程中因为变异和分割形成的单调沉闷音符，可以执行合并重复音符向，即将染色体中任意相同音高的连续音符合并为等长音符。

1.5 算法终止条件

算法终止条件与适应度函数有关。当选定适应度函数后，借助人的理解来判定乐曲的优劣，采用自适应评价适应度函数时，利用最大迭代次数或作品相似度作为终止条件[17]。

2 遗传算法的频谱作曲

本节中提出基于遗传算法的交互式作曲系统。通过适应度函数进行乐曲评价。由于作曲过程中的乐曲质量的提高，只需要较少的迭代次数就能获得满意的乐曲，大大降低了作曲时间。对于乐曲中存在的单个音符在节奏、和弦、旋律上的不同组合，产生的数量过于庞大，系统选择对特定子集进行处理来合理减少搜索空间计算方法。在乐曲信息的编码过程中，音乐知识和规律是作曲系统中构筑乐曲的必要因素，而规则是通过适应度函数执行的，本研究采用人对个体的评价作为适应度函数来验证群体对规则的遵守情况，降低算法对乐理知识的高要求。

2.1 乐曲结构

通常音乐作品是由一个主调声部和多个复调声部构成。为简化运算，只产生单声部乐曲，乐曲长度采用4节拍，拍号为4/4，为便于对乐曲细微变化处进行准确评价，形成易识别乐曲，将乐曲调号定为C大调，主音固定在谱表小字一组c上。音符时值以整数方式表示，以十六分音符为准，定义值为1，其他音符按表1所示定义，休止符与普通音符相同。由于系统中主音固定在小字一组c上，因此取各音与c间的半音倍数对应整数值作为音符音阶，拍子的力度同样采用整数值进行定义，乐曲不同音符、音程和力度的编码处理,如表1所示。

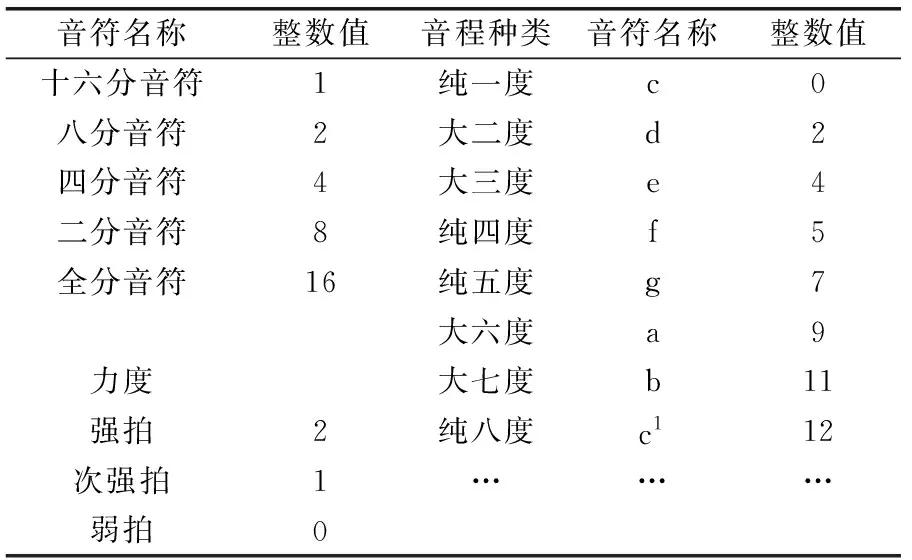
表1 乐曲的编码处理

2.2 乐曲表示方法

由单个或多个音符以一定的形式组成乐曲，将潜在的信息表示出来。在本研究系统中，单个音符以{音程种类，音符时值，拍子力度}的整数值形式来表示，如图3所示。

{(14,2,2),(11,2,2),(9,2,2),(11,2,),(14,8,2)},{(14,2,2),(11,2,1),(9,2,2),(11,2,1),(14,8,2)}图3 乐曲的整数法表示

选择一段《丢手绢》的五线谱，用整数的表示方法。其中小括号内表示一个音符信息，大括号为一小节音符信息。

2.3 交叉变异方法

系统提供了音程交叉、时值交叉、力度交叉3种方式，音程交叉方式下的染色体变化,如图4所示。

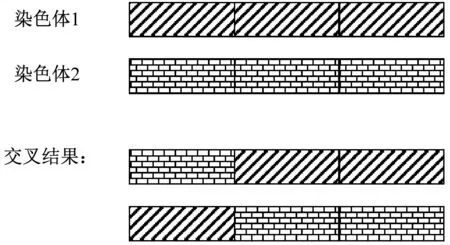
图4 染色体的音程交叉算法

同时，可定义变异概率值，对某一段染色体某个组成部分进行修改、删除等操作。

2.4 算法作曲实现

选取儿童音乐《小星星》作为初始种群，在适应度函数下，通过异常算法交叉、变异操作生成新的乐曲，如图5所示。

(a) 初始五线谱

(b) 进化五线谱图5 频谱乐曲的生成

图5(a)为乐曲的初始五线谱。采用二进制编码方式对乐曲进行编码操作，并根据3种交叉方式，以及5%的随机变异率进行交叉变异操作。通过随机替换单个音符、改变小节音符和音符序列、复制音符片段进化乐曲。对乐曲进行迭代计算，当进化到50次时，去除其中存在的旋流音以及不和谐音符，获得新的五线谱如图5(b)所示。

对比新旧两个五线谱可以发现，生成新的乐曲以很快地收敛速度达到适应值。采用模式匹配时，染色体权重取值相较于其他特征值更为重要，若模式匹配进化过程中超过权重阈值，则形成单调重复的五线谱，毫无律动性。

3 总结

将遗传算法应用于作曲中，获得了一种新的计算机算法频谱作曲方式。通过遗传算法将乐谱转化为数字编码形式，以人作为适应度函数，进行交叉、变异算子形成新的乐曲。通过实例分析可以看出，遗传算法应用于作曲中的效果与系统的音乐知识表现程度相关，当规则越充分，则作品呈现度越高，算法在小节音乐作曲中获得了较好的效果。但由于算法是一类随机、启发式的搜索方法，制作新乐曲的效果不能与作曲家相提并论，后续可以将神经网络引入到遗传算法中，实现对更长乐曲制作的算法改良。