Magnetic dynamics of two-dimensional itinerant ferromagnet Fe3GeTe2∗

Lijun Ni(倪丽君),Zhendong Chen(陈振东),5,Wei Li(李威),Xianyang Lu(陆显扬),Yu Yan(严羽),Longlong Zhang(张龙龙),Chunjie Yan(晏春杰),Yang Chen(陈阳),Yaoyu Gu(顾耀玉),Yao Li(黎遥),Rong Zhang(张荣),Ya Zhai(翟亚),Ronghua Liu(刘荣华),†,Yi Yang(杨燚),‡,and Yongbing Xu(徐永兵),4,§

1Jiangsu Provincial Key Laboratory of Advanced Photonic and Electronic Materials,School of Electronic Science and Engineering,Nanjing University,Nanjing 210093,China

2Jiangsu Provincial Key Laboratory for Nanotechnology,School of Physics,Nanjing University,Nanjing 210093,China

3Department of Physics,Southeast University,Nanjing 211189,China

4York-Nanjing Joint Centre for Spintronics and NanoEngineering,Department of Electronic Engineering,University of York,York YO10 5DD,United Kingdom

5Jiangsu Key Laboratory of Opto-Electronic Technology,Center for Quantum Transport and Thermal Energy Science,School of Physics and Technology,Nanjing Normal University,Nanjing 210023,China

Keywords:two-dimensional ferromagnet,ferromagnetic resonance,magnetic anisotropy,magnetic damping

During the last two decades,two-dimensional(2D)materials such as graphene and transition-metal dichalcogenides,exhibiting many attractive properties,have been extensively studied.[1–4]The 2D intrinsic ferromagnetic vdW crystals were predicted to have promising spintronic applications[5–8]with high data storage density,faster response,and lowpower dissipation.[9,10]It is also of great interest as the building block for engineering spintronic vdW heterostructures.[11]Recent experiments have demonstrated that it is possible to obtain 2D ferromagnetic order in CrI3-and CrSiTe3-type compounds.[12–17]However,bulk CrI3,CrGeTe3,and CrSiTe3exhibit the FM orders below 68 K,61 K,and 33 K,respectively,which are much lower than room temperature(RT).Among the predicted and experimentally observed vdW ferromagnetic materials,as an itinerant ferromagnet,[18]the single crystalline FGT stands out with a relatively high TCin its bulk state,ranging from 150 K–220 K depending on Fe deficiencies.[19–24]Up to now,various experimental investigations such as anomalous Hall effect,[25]DC magnetization,[20,23]chemical substitution,[26,27]and magnetic microstructure[28]have been carried out on FGT.However,there still lacks the magnetic dynamics study of this 2D vdW itinerant ferromagnet until now.

Three-dimensional(3D)microwave cavity-based electron-spin-resonance spectrometer as a high sensitivity technique has been widely used for the magnetic analysis of ferri-and para-magnetic components within environmental samples and characterization of dynamic properties of magnetic materials.[29,30]According to the resonance field(Hr)and linewidth(ΔHpp)of ferromagnetic resonance(FMR),[31–33]one can obtain magnetic anisotropy K1and the magnetic damping of magnetic materials.Since magnetic relaxation processes govern the efficiency and determine the performance of magnetic devices,including hard drives,magnetic random access memories,magnetic logic devices,and magnetic field sensors,therefore obtained damping experimentally,as well as dynamic magnetic properties of magnetic materials and heterostructures,is crucial for their application in potential spintronic devices.Generally,it is crucial to obtain the FMR spectra,as this is the first step for further investigating the dynamic properties of 2D vdW ferromagnets.Hence,it is necessary to obtain the FMR spectra and understand the essential magnetization dynamics of bulk FGT for future functional spintronic devices containing FGT metallic ferromagnet near room temperature.

In this paper,we first established the static magnetic properties of the single crystal FGT bulk.The static magnetization properties were obtained by studying temperature-and magnetic field-dependent magnetic susceptibility using a superconducting quantum interference device(SQUID)magnetometer.And we determined magnetic anisotropy constant K1from the SQUID measurements.More importantly,we have conducted the dynamic studies with electron-spinresonance(ESR)spectrometer at cryogenic temperature,and observed the FMR spectra in the intrinsic 2D ferromagnet FGT.Temperature-dependent magnetic anisotropy constant K1and the effective magnetic dampingαeffhave been calculated from the isothermal angular dependent resonance field Hrand linewidth.The K1exhibited an expected decreasing behavior near TC.However,the effective magnetic damping αeffas large as 0.58 was obtained,showing little temperature dependence.Our results provide significant insight into the magnetization dynamics of 2D vdW itinerant ferromagnet FGT,going beyond the previously reported static observation.

High-quality FGT single crystals were synthsized by the chemical vapor transport method.First,the pure powders Fe(99.998%),Ge(99.999%),and Te(99.999%)were weighed out in a stoichiometric ratio of 3:1:5.The elements were blended and placed,along with solid iodine I2as a transport agent,into an evacuated quartz tube,which was evacuated of air before sealing.Then,the sealed tube was placed in a furnace with a temperature gradient between 700°C and 650°C for one week.The starting mixed constituents were placed at the hot end,and the single crystals precipitated on the cold end of the tube.Finally,the FGT single crystals were analyzed with x-ray diffraction(XRD).Temperature-and fieldmagnetization measurements were carried out using a SQUID magnetometer.The out-of-plane angular dependence of FMR was measured using an electron-spin-resonance spectrometer due to its high sensitivity at a microwave frequency of 9.48 GHz.Before the measurements began,an external field had been set along the easy magnetic axis(i.e.,c-axis)of FGT.And then,the measurements were implemented to vary the angle as the samples were rotated.

FGT is a layered hexagonal structure(the P63/mmc space group).[23]In Fig.1(a),the crystal structure of FGT contains Fe3Ge slabs separated by a so-called vdW gap between adjacent Te layers.The Fe atoms in the unit cell occupy two inequivalent Wyckoff sites Fe1 and Fe2.Figure 1(b)presents a 2θXRD scan;only(00l)peaks are detected,indicating that our FGT samples exhibit the high single-crystalline quality,and the crystal surface is normal to the c-axis with the plateshaped surface parallel to the ab-plane.Figure 1(c)shows the temperature dependence of magnetization M(T)measured under H=100 Oe applied in parallel to the c-axis.An obvious paramagnetic(PM)to FM transition is observed.Besides,the ZFC and FC curves show significant splitting at low temperatures.TC≈204 K is roughly determined from the minima of the dM/dT curve with an external field of 2 T parallel to the c-axis,as indicated by the orange arrow in the inset of Fig.1(c).Figure 1(d)shows the field dependence of hysteresis loops at various temperatures for H‖c-axis.We observe that saturation magnetization Msgradually decreases with the temperature increasing.Moreover,Msof FGT at 185 K approximately drops significantly by two orders of magnitude as compared with that at 2 K,as plotted in Fig.1(f).To confirm the magnetic anisotropy of FGT,we further perform isothermal magnetization loops at 2 K for H‖ab-plane and H‖c-axis[Fig.1(e)].The magnetization saturation with H‖c-axis and H‖ab-plane at 2 K is reached for H≈4.9 kOe and 35 kOe,respectively.The saturation field for H‖c-axis is much smaller than that for H‖ab-plane,indicating that the magnetic behavior is highly anisotropic with its easy magnetic axis along the crystal’s c-axis.This conclusion is in good agreement with previous results.[25,28]

In addition to H‖c-axis,we also measure the field dependence of hysteresis loops at various temperatures for H‖abplane,as shown in Fig.2(a).Figure 2(b)represents magnetization measured at T=185 K with the external field H‖c-axis and H‖ab-plane.Thus,we can determine K1using the following formula:

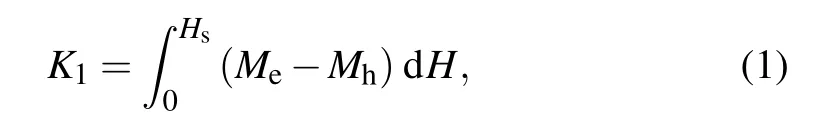
where Hsis the saturation magnetic field with the external magnetic field H‖ab-plane during the measurement.Meand Mhare the magnetization obtained with the external fields H‖c-axis and H‖ab-plane,respectively.The obtained K1is in the range of(3.8–0.4)×106erg/cc in the 2–205 K range,as shown in Fig.2(c).And,the K1decreases monotonically with increasing temperature.

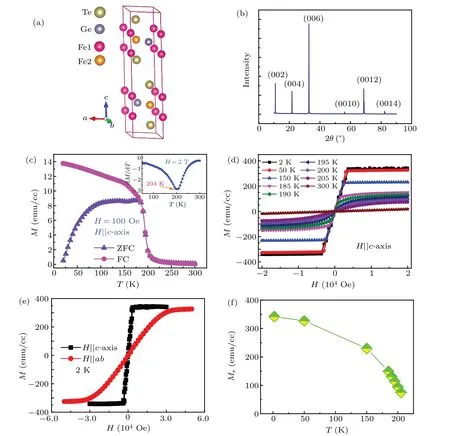
Fig.1.(a)Crystal structure of FGT from side.(b)XRD spectrum of a bulk FGT crystal.(c)Temperature dependence of magnetization for bulk FGT with zero-field-cooling(ZFC)and field-cooling(FC)modes measured with the external magnetic field H=100 Oe along the c-axis.Insert shows the derivative magnetization dM/dT vs.T in the applied field along the c-axis.Arrow denotes the minima of the dM/dT curve,determining the TC of FGT.(d)Field dependence of magnetization for FGT measured at 2–300 K with the external magnetic field H along the c-axis.(e)Magnetization is measured at T=2 K with the external field H‖c-axis and H‖ab-plane,respectively.(f)Saturation magnetization as a function of temperature(2–300 K).

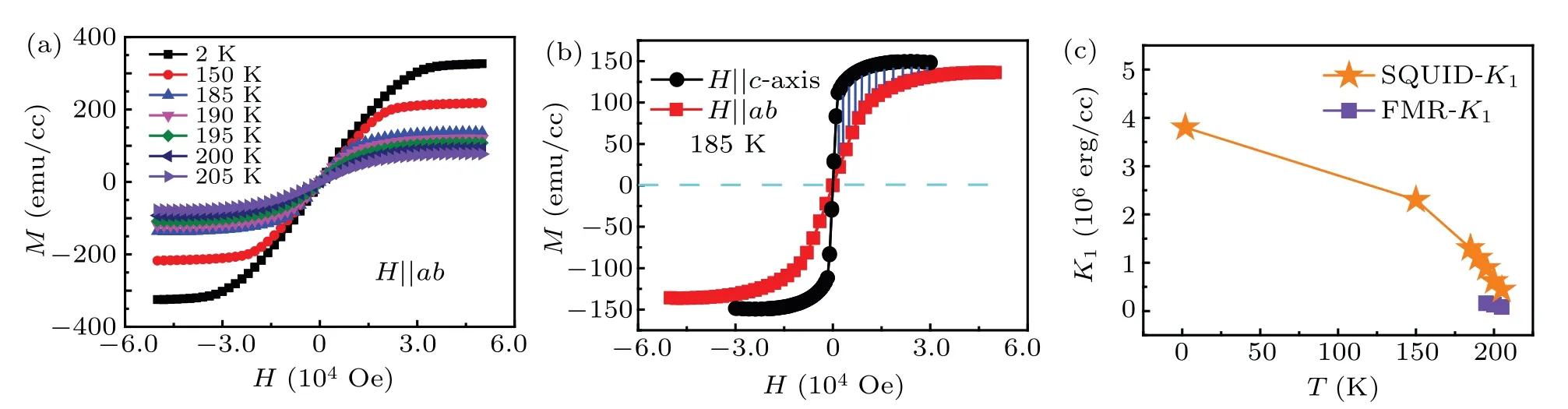
Fig.2.(a)Field-dependent magnetization of FGT with the external magnetic field H‖ab-plane measured in the range of 2–205 K.(b)Magnetization measured at T=185 K with the external field H‖c-axis and H‖ab-plane,respectively.The shaded area,surrounded by the magnetization curves when H‖c-axis and H‖ab-plane.(c)Temperature-dependent uniaxial magnetic anisotropy constant K1,calculated by fitting the angular-dependent Hr(violet squares)at 195–205 K and using the M–H loops(orange stars)at 2–205 K,respectively.

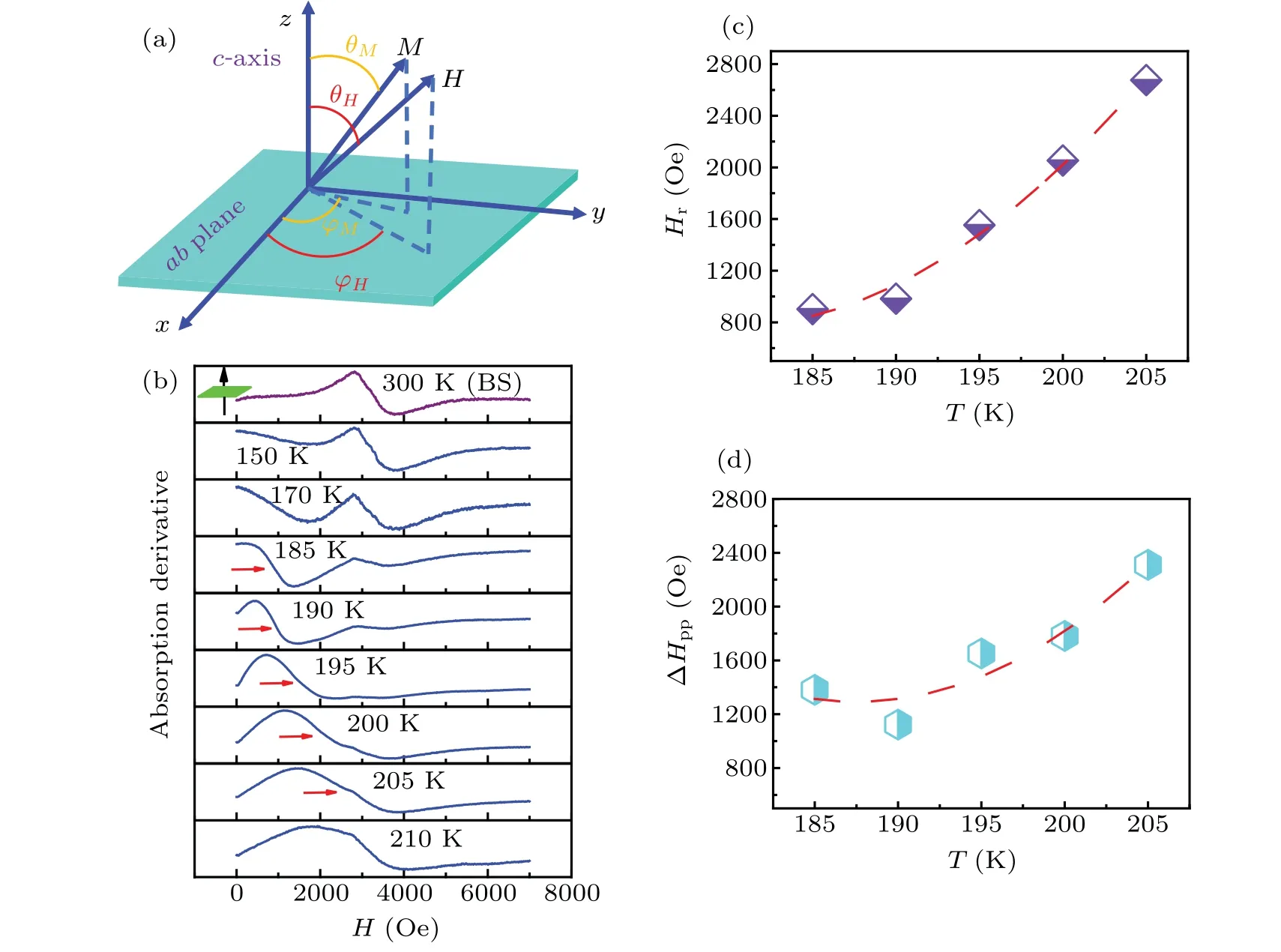
Fig.3.(a)The sketch of the coordinate system used to measure and analyze FMR.All FMR experiments are measured at a microwave frequency of 9.48 GHz.(b)FMR spectra of FGT with various temperatures(T=150,170,185,190,195,200,205,210 and 300 K)under the external magnetic field H‖c-axis(θH=0°;θM=0°).And the red arrow indicates the Hr of FMR spectrum.(c)–(d)Temperature dependences of Hr(c)andΔHpp(d),obtained from the FMR spectra in(b).The broken lines in(c)and(d)are the guide for the eyes.

To explore the magnetization dynamics of FGT,we further perform the FMR measurement of single-crystal FGT.Figure 3(a)represents a sketch of the FMR coordinate system,whereφMandφHare the azimuthal angles,andθMandθHare the polar angles of the magnetization M and the DC external field H,respectively.Figure 3(b)shows the field dependence of FMR spectra for various temperatures(T=150,170,185,190,195,200,205,210 and 300 K)with H‖c-axis(i.e.,in the perpendicular configuration,θH=0°;θM=0°).The purple curve in Fig.3(b)is the background signal because FGT enters into a paramagnetic state at 300 K and it is also the same as the signal of the empty cavity without a sample.Near TCfrom 185 K to 210 K,the typical FMR spectra are observed in the ferromagnetic phase of FGT.The observed FMR signals below 210 K illustrate a fundamental fact that the precession of magnetization of FGT single crystal can be driven by an external microwave signal,like most of the ferromagnetic materials.[30,31,33–36]Moreover,this observation is consistent with the TC≈204 K determined from the measurement of temperature-dependent magnetization.In addition,from Fig.3(b),we also find that Hrgradually shifts to zero external magnetic field with decreasing temperature,indicating that the natural resonance frequency of FGT due to its magnetic anisotropy is higher than the external excitation frequency 9.48 GHz for T<180 K.It is well known that Hrvalue corresponds to the intersection of the FMR spectrum with the base line.The extracted Hrfrom Fig.3(b)for the temperature of 185–205 K is displayed in Fig.3(c),which more intuitively presents a fall of Hrwith decreasing temperature.The FMR spectrum is broadened with increasing temperature while maintaining its derivative Lorentzian-like curve shape in the 185–205 K range.ΔHppis the width between the positive and negative peaks of the FMR spectrum.In Fig.3(d),the minimum value ofΔHppis larger than 1000 Oe,suggesting that this FGT system may have an unexpected high magnetic damping constant.In contrast with some other 2D ferromagnets,e.g.,Cr1/3NbS3and CrGeTe3,FGT has a weak FMR signal and very broad linewidth.[9,37]The FMR linewidth can generally be considered from three origins:(i)Gilbert damping,(ii)two magnon scattering,and(iii)sample magnetic inhomogeneities.The large Gilbert damping was reported previously in the Ni80Fe20film doped with heavy rare earth atoms.[38]In the doped Ni80Fe20film,the large linewidth(>1000 Oe at 22 GHz)corresponds to the damping value of 0.1–0.2.According to the modified Kambersk´y’s spin–orbital torque correlation theory,[39]for a ferromagnetic metal,two competing contributions give rise to intrinsic Gilbert damping:intraband electron–hole transitions and interband electron–hole transitions.The former contributes a conductivity-like term(decreasing with the electron scattering rateΓ),while the latter gives a resistivity-like term(increasing withΓ).For our FGT sample,the resistivity-like term may dominate the Gilbert damping.And,the existence of Fe vacancies also effectively enhances the scattering rate,thereby promoting interband electron–hole transitions.Meanwhile,due to more electron scatterings at the higher temperature,theΔHppincreases with temperature.Furthermore,theΔHpprising as the temperature increases is consistent with the behavior that the coherent FMR dynamics(where the wave vector k=0)continuously evolve into an incoherent process due to the strong thermal excitation of magnon,[40]resulting in the magnon scattering and the inconsistency of magnetic moments continually increasing and broadeningΔHpp.The temperature broadening linewidth or enhancing magnetic damping phenomena are generally observed in numerous magnetic materials.[41,42]Besides,the magnetization inhomogeneity is also expected to significantly influence the observed broad FMR linewidth due to the large magnetic anisotropy and nucleation of magnetic multidomain.

To quantificationally estimate the magnetic damping of FGT,we further carry out measurements of the out-of-plane angular dependence(i.e.,φM=φH=π/2)of FMR at the fixed microwave frequency of 9.48 GHz.Figure 4(a)shows the representative FMR spectra for differentθHat 190 K.The value of Hris enhanced as the external magnetic field H varies from the out-of-plane(H‖c-axis)to the in-plane(H‖ab-plane)direction.Figure 4(b)shows the out-of-plane angular dependence of Hrfor the temperature from 185 K to 200 K,and open circles represent the experimental data.Moreover,the curve of Hrvs.θHexhibits only one peak.These measurement results further confirm that FGT has uniaxial magnetic anisotropy,and the easy axis is along the c-axis as mentioned above.Figure 4(c)displays the experimentalΔHppas a function ofθHfor different temperatures,indicated by blue globules.

Fig.4.(a)The typical FMR spectra of FGT measured at T=190 K with different anglesθH=0°,45°,and 90°.(b)Angular dependence of resonance field Hr of FGT for various temperatures T=185 K,190 K,195 K,and 200 K.Open circles represent the experimental data and red lines show the fitting curve of Hr.(c)Angular dependence of peak-to-peak linewidthΔHpp with T=185 K,190 K,195 K,and 200 K.Blue globules indicate the experimental data and orange lines are the calculatedΔHpp.

Based on a single magnetic domain model for the FGT sample under FMR conditions,we analyze the data ofθHvariation of HrandΔHppquantitatively.First,we focus on the data θHvs.Hr.We describe the resonant peaks by the Smit–Beljers equation[43,44]

whereω=2πf with a microwave frequency f=9.48 GHz.γis the gyromagnetic ratio.F is the free energy density given by the following expression for the FGT sample:[30,45]

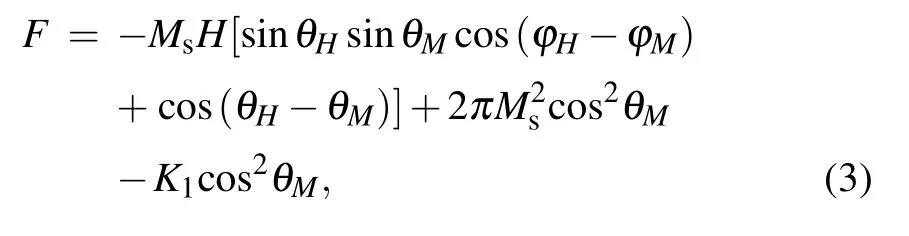
where K1is the perpendicular magnetic anisotropy constant.The first,second,and third terms represent the Zeemanenergy density describing the coupling between the magnetization vector M and the external magnetic field H,the shape anisotropy energy,and the uniaxial magnetocrystalline anisotropy energy,respectively.In our case,because the lateral dimensions in the ab-plane are much larger than the thickness of the FGT crystal along the c-axis,the shape of the measured platelet-like FGT crystal is described by the demagnetization factors(Nx=Ny=0,Nz=1)of an extended flat plate.Because ofφM=φH=π/2,we obtain the following equation by deducing from Eq.(3):[45]

Here,4πMeffis the effective demagnetizing field,defined by

where Hk=2K1/Msis the perpendicular magnetic anisotropy field.The experimental data of the angular dependence of Hrare fitted by using Eq.(4)with bothγand 4πMeffused as fitting parameters.The azimuthal angle of magnetizationθMis determined concurrently by solving the equation

The solid red lines in Fig.4(b)show the fitting results of resonant field Hras a function of the external field orientation θH.The temperature dependence of K1in the range of 195–205 K is summarized in Fig.2(c).The K1is in the range of(1.6–0.8)×105erg/cc from 195 K to 205 K.Meanwhile,the K1obtained from magnetization SQUID-measurements mentioned above has values of(8.9–4.4)×105erg/cc from 195 K to 205 K.We observe that there is the same order of magnitude of K1near TCof FGT calculated using two different methods.Furthermore,the slight deviation of K1value may be due to the different methods(i.e.,the dynamically and the statically determined K1)and domain structures at the angleθHclose to in-plane for the FMR-method.We note that it is more thorough and reliable to obtain the anisotropic constant K1from the M–H loops measurements.

Second,we turn to the linewidth of FMRΔHppanalysis in Fig.4(c).For out-of-plane measurements,ΔHppcan be expressed as[29,43]

Figure 5 shows no apparent dependence ofαeffon temperature in the range of 185–205 K.The overallαeffvalues are large with an average damping value of about 0.58.The αeffof FGT is much larger than that of other 2D ferromagnets such as Cr1/3NbS3,CrGeTe3and magnetic metal films CoFeB[41]and Fe.[47]There have three possible sources accounting for the large dampingαeffvalue.One source is that the FGT as 2D vdW itinerant ferromagnet itself owns a huge intrinsic Gilbert damping.The second source may be related to the strong magnon scattering process as an additional magnetic relaxation channel near TCand causes the enhancement of linewidth and damping.The third source is the magnetization inhomogeneity of the FGT sample.

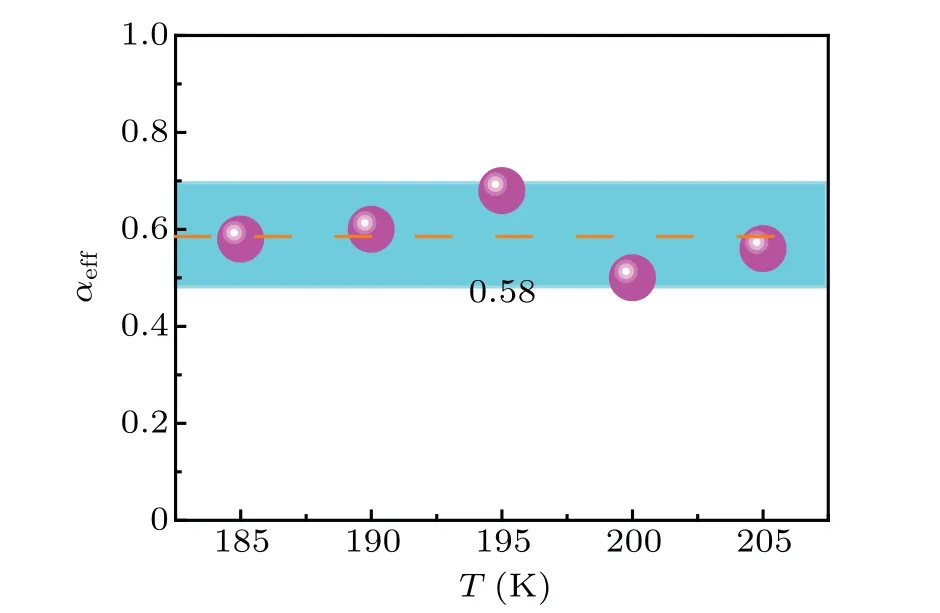
Fig.5.Effective damping constantαeff as a function of temperature.The orange dash line represents the average value of 0.58.

Note that our current FMR results with the relatively limited temperature range due to a low excitation frequency～9.48 GHz(or a low magnetic field range)prevent us from extracting the magnetic damping coefficient accurately and identifying the behind mechanism.The FMR spectra experiments with a large magnetic field range or high excitation frequency and first-principles calculations about damping or the theoretical models need to be performed to explore further the behind mechanism of such larger magnetic damping constant in this 2D vdW itinerant ferromagnet.

In summary,we characterized the static magnetization of the bulk FGT single crystal with a TCaround 204 K and obtained the temperature-dependent uniaxial magnetic anisotropy constant K1.Furthermore,the FMR spectra were also obtained by ESR from 185 K to TCwith a fixed frequency of 9.48 GHz.The minimum linewidthΔHppis larger than 1000 Oe when H‖c-axis.We also estimated the damping constant quantificationally from the out-of-plane angular dependence of FMR spectra,and found that the effective magnetic dampingαeffis about 0.58 near TC.Our results not only provide insights into the magnetic dynamical properties of 2D vdW itinerant ferromagnet FGT,but also can significantly facilitate its future applications in spintronic devices.