Barrier or easy-flow channel:The role of grain boundary acting on vortex motion in type-II superconductors∗

Yu Liu(刘宇),Xiao-Fan Gou(苟晓凡),‡,and Feng Xue(薛峰)

College of Mechanics and Materials,Hohai University,Nanjing 211100,China

Keywords:type-II superconductors,grain boundary(GB),vortex motion,competition effect,GB strength,the relative disorder strengthαp/αv

1.Introduction

The type-II superconductors allow for the penetration of quantized magnetic flux,viz.vortex lines(vortex for short hereafter)when being subjected to sufficiently strong external magnetic field.The motion of the vortices in superconductors is not only about the micro physics,more importantly,macroscopically dominates the superconductivity,for example the current-carrying capacity–critical current density Jc.[1–5]Essentially,vortex motion mainly results from the balance of the electromagnetic force(i.e.,the Lorentz force FL=J×B)and pining force at pining centers.The pining force on vortices,as an intrinsic characteristic of superconductors,is fundamentally determined by the pining strength of defects.These various defects in superconductors including second phases,grain boundaries,oxygen-vacancy clusters,irradiation-caused defects,dislocations,and growth flux inclusions are found to act as pinning sites for vortex motion against the driven electromagnetic force in type-II superconductors.[6–13]Among them,grain boundaries(GBs)are the most typical anisotropic pinning defects of the cuprate compound YBa2Cu3O7−x(YBCO).And therefore,study of the effect of GB on vortex motion in type-II superconductors has to be very significant not only for understanding their basic physics but also for the materials fabrication and many potential applications.

GB in type-II superconductors and the effect on vortex motion have been studied in various researches performed on thin films and bulk samples.[14–22]By means of magnetooptical and magnetic hysteresis measurements,GB in superconductors was found to play a strong obstructive barrier for vortex motion in most cases,and later studies further indicated that GB can also be an easy-flow channel of vortices under certain conditions.[23,24]Recently more researches focused on the dependence of the GB angle on vortex motion.[25,26]Thus,a question arises that what is exactly the role of GB on vortex motion and how does it affect.So far it has been still unclear and remains to be future studied.

In order to answer this question,deeply and completely understanding the effect of GB on vortex motion in superconductors has to be very significant.So,in the present work,we firstly developed a large scale molecular dynamic model,in which the GB structure was created by uniformly distributed special sites and an attractive well formed with the local electric fields.And besides,random structureless point pinning centers in superconductor were also taken into account in this model.Further performed with the LAMMPS code to deal with vortex–vortex,vortex–pin,and vortex–GB interactions,we tried to understand the role of GB on vortex motion,and reveal the effect mechanism of GB and the intrinsic correlations.In addition,on this molecular dynamic model and taking the superconductor YBCO as example with GB,we obtained a clear and visual knowledge of three typical trajectories of the vortices in the area near the grain boundary corresponding to the different relation of the average velocity with the driving force.

2.Calculation model and approach

Following the previous studies in regard to the GB effect on the vortex motion in the mixed state of superconductors,that is,the GB acting as easy-flow channels for vortices moving parallel to it and as an obstructive barrier for them perpendicular to it,here we consider the behavior of the vortices in the vicinity of the GB analogous to the motion of charge carriers induced by an electric field.As shown in Fig.1,the GB can be actually modeled as a potential well in which a series of dislocations(red dots)were arranged along the GB and meanwhile the local electric fields were applied to be perpendicular to the direction of the grain boundary on both sides.As charge carriers,all the vortices are subjected to an additional electric force when they move into the specific area to model the GB as a potential well showing that the GBs are anisotropic pinning centers.[27–29]The direction of the electric force that the vortices subjected to in the local electric field is perpendicular to the GB and always points to inside of the GB region since the local electric fields on both sides of the GB equal in magnitude(due to quantities of twin boundaries existing in the cuprate superconductors)but opposite in direction.

Fig.1.The calculation model:a magnetic vortex pinning area of type-II superconductors with the grain boundary(GB).A large number of solid black spots represent magnetic vortices,and the rectangular band area between the red dotted lines indicates just the GB,2d andθare the width of the GB and the angle between the GB and the applied current respectively.In the GB region,a series of bigger red dots represent dislocations,and the red arrows on magnetic vortices represent the directions of electric forces.I and H present the transport current and applied magnetic field,respectively.

Through the calculation model,we can study NvAbrikosov vortices interacting with the GB and Nprandom pins in a two-dimensional(2D)slice in the x–y rectangular system of the three-dimensional(3D)slab.The x axis is taken along the orientation of the applied current so that the Lorentz force only has a y component.In calculation,in order to use reasonably the periodic boundary conditions in the x-axis and y-axis directions for both GB and pinning sites,the slice is fixed with the GB in the center normal to the edge just as shown in Fig.1.And the variation of the angleθis realized by changing the direction of the applied current.Considering the London limitλL≫ξs,whereλLis the penetration length andξsis the superconducting coherence length,we can treat vortices as point particles.In the present calculation,we employed the LAMMPS molecular dynamics code to perform numerical simulation.

The equation of the time evolution of the vortex i at the position rican be given as[30,31]

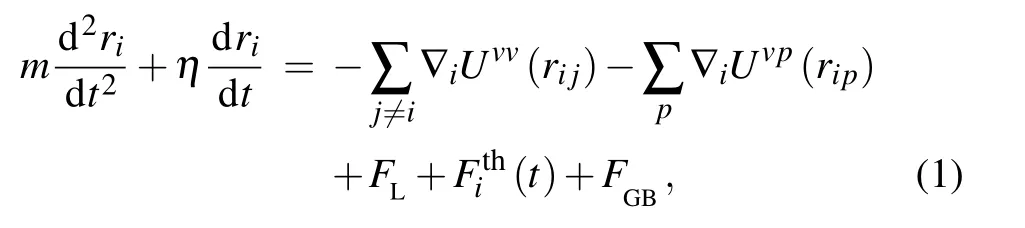
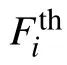
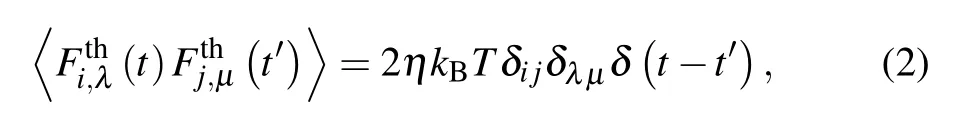
where kBis the Boltzmann constant,T is the temperature,and λ,µ=x,y.The vortex–vortex repulsive interaction is described by a modified Bessel function as[30,31]

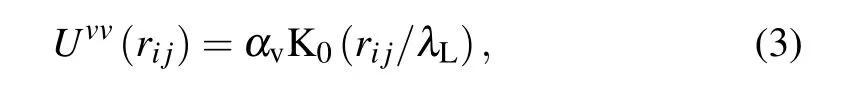
and the attractive pinning potential[30,31]is described by

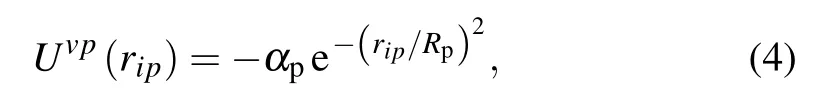
where Rpthe radius of the pins,andαvandαpare tunable parameters,which depend on the relative strengths of the vortex–vortex and vortex–pin interactions.The FGBis the GB force acting on the vortices,here we took account of the action of the local electric fields described in the calculation model and the effect of the series of dislocations acting as special uniform pinning centers.The related parameters E(the electric field intensity)and q(charge of the vortices)are tunable parameters.The pinning potential of the special pins along the GB is given by

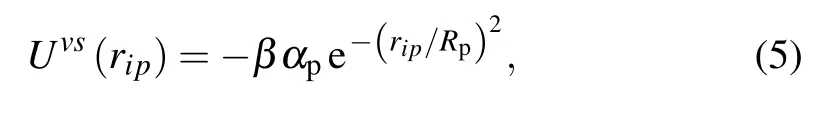
whereβis a tunable coefficient.The action of the local electric field occurs when the vortices moving into the specified area in the vicinity of the GB,and disappears after the vortices moving out the area.In simulation,we setαv=2.83×103λLε,whereεis an energy per unit length.The cutoff radius in the LAMMPS code rc=6.5λLand the radius of the pins Rp=0.22λL.A unit system was used here,in whichλL=1,ε=1,and kB=1.

3.Results and discussion

3.1.Vortex motion and the competition mechanism of determining the GB role

The samples with the presence of pins or both GB and pins display different responses with the external driving force.However,there all exists the critical depinning force Fcabove which the system starts sliding from a pinned state.In order to check for the hysteresis behavior of vortex motion,several trial values can be chosen in the neighboring range of the force initially obtained to confirm its accurate value for each critical force.On previous researches,[31]we already know that,in the elastic regime,all the vortices depin together and move orderly as one,which forming a topologically ordered structure with coupled channels,but flow along the channels around pinned regions of vortices which indicates the integrity of the lattice being compromised in the plastic case.To completely understand the vortex motion,in this work we can study both the elastic and plastic dynamics of vortices through a combined parameter—the relative disorder strengthαp/αv.It is defined as the ratio of vortex–pin and vortex–vortex interactions,and can characterize the level of the relative disorder on vortex motion in a system.Generally,we can choose the value small enough(for example,αp/αv=5×10−3)to enforce elastic behavior or big enough(for example,αp/αv=5×10−2)to cause plastic behavior.

Firstly,we calculated the critical driving force Fc,and obtained the normalized Fcby F0(i.e.,the critical driving force for the sample without GB)varying with the GB strength FGBboth in the elastic and plastic regimes under three different GB angles.Here the applied electric force FGB=Eq represents the total GB strength since the pinning force from the special pins along the GB keeps constant.As shown in Fig.2,the same things in common are that the normalized critical driving force varies with no obvious decrease when the GB strength is lower(less than about 10−1for elastic regime and 1.5 for plastic regime),while rapidly declines when the GB strength is much higher(larger than 10−1and close to 100for elastic regime and larger than 1.5 and close to 1.8 for plastic regime).The smaller the grain boundary angle is,the larger the normalized critical driving force is.And with referring to the result(identically equal to 1)for the sample without GB,generally,the critical driving forces vary from greater to lower than 1(no matter what regime it is in)except for the situation for the cases of GB angle 60°in the elastic regime(Fig.2(a))and GB angle 45°&60°in the plastic regime(Fig.2(b)),and in which the force keeps lower than 1 under no GB condition as the intrinsic behavior effected and concealed by the weight of the angle.

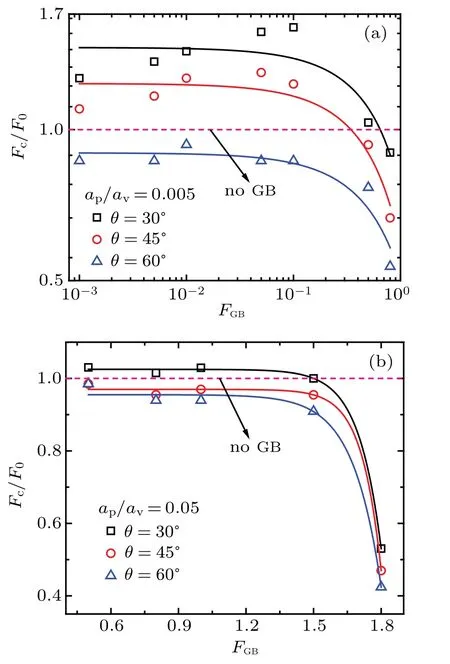
Fig.2.The normalized critical driving force Fc/F0 versus the GB strength FGB in(a)the elastic regime and(b)plastic regime for the sample of size(Lx,Ly)=with 384 vortices in three cases of different GB angles(F0 is the critical driving force for the sample without GB corresponding to specific relative disorder strengthαp/αv,the same below).

The results in Fig.3 show that,with the relative disorder strengthαp/αvincreasing for all three cases of GB angles,the critical driving force decreases across the value in the case of no GB,i.e.,the value from greater than 1 to less than 1,and the general trend is not affected by different GB angles.It means that the GB acts as an easy-flow channel for vortex motion as the critical driving force lower than that for the case of no GB,while as a strong barrier with the critical driving force higher than that in no GB situation.

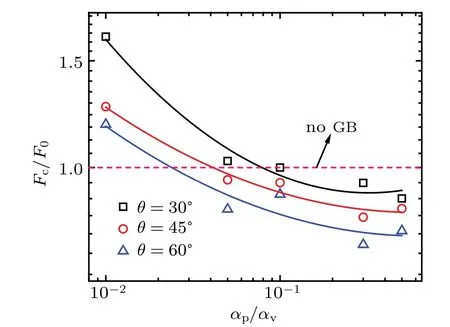
Fig.3.The normalized critical driving force Fc/F0 versus the relative disorder strengthαp/αv in three cases of different GB angles.The specific GB strength is fixed as 10−1.

Combined with the results in Fig.2,we discussed as follows:(i)the role of GB on vortex motion(or vortices start to move)is not unchangeable,but changes from obstruction(corresponding to the situation Fc/F0>1,it means obstructive action on vortices)to promotion(i.e.,Fc/F0<1,it means promotive action);(ii)the role changing on vortex motion is related to the relative disorder strengthαp/αvin no GB region,the GB angle and strength.In other words,this role changing depends on the relative strength of the restriction on vortices from pining centers in no GB region and GB region itself;(iii)more intrinsically,there actually exists a competition effect between the internal(in GB region)grain boundary strength and the external(in no GB region)effect intensity(the intensity can be characterized by the relative disorder strengthαp/αvor inversely the relative order strengthαv/αp).In conclusion,it is such the competitive behavior that determines the role of GB on vortex dynamics being a strong barrier or an easy-flow channel.Specifically,in the elastic depinning transition regime,the vortices have strong integrity and the pinning effect gets relatively weak,and consequently the long-range pattern is destroyed by GB.However,in the plastic depinning transition regime,the integrity of the vortices is relatively weak and the pinning effect is comparatively strong,and consequently GB primarily overcome the attraction of pinning centers.In a word,the competition exists in the contrast of the action on vortex dynamics from the GB region to no GB region.

The competition effect has to be of crucial importance on the role of GB over the vortex dynamics in the mixed state.Moreover,the existence of the competition effect can offer a preferable foundation for the optimization of superconducting transport properties by adjusting the correlation between the internal grain boundary strength and the external effect intensity.Indeed,various approaches developed,such as doped grain boundary,artificial pinning sites,and the arrangement of the pinning centers for adjusting and controlling the nanostructure of type-II superconducting materials,have been verified to be viable to transform the pinning effects.

Besides the competition effect,the relative orientation of flux movement with respect to the direction of GB has influence on the role of GB as well.As shown in Fig.4,no matter in which the elastic regime(Fig.4(a))or the plastic regime(Fig.4(b)),the critical driving forces sharply drops down when the angle is in the range of 0°–15°,and then gently decreases,and again rapidly goes down when the angle is close to 90°(for the plastic regime).And in other words,the critical driving forces decreases across the value in the case of no GB(i.e.,the Fc/F0varies from greater than 1 to less than 1).The variation of the critical driving force again indicates that the role of the GB on vortex motion can transform between a barrier and an easy-flow pathway.In addition,the lattice is more likely to move or be teared with the angleθgrowing,which means the system depinning transition becomes easier.

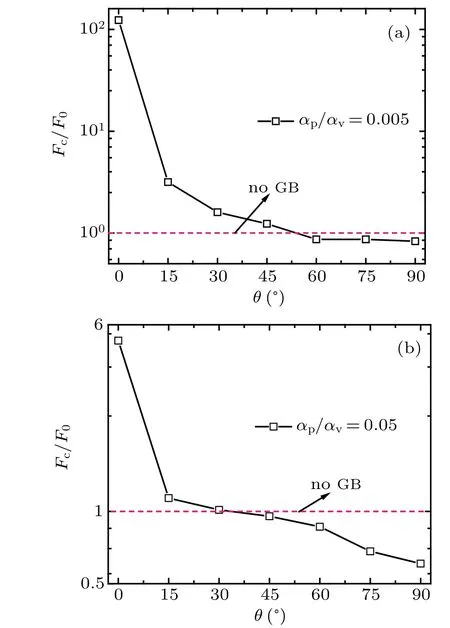
Fig.4.The normalized critical driving force Fc/F0 varying with the angleθ in(a)the elastic regime and(b)the plastic regime.The specific GB strength is fixed as 10−1.

3.2.Impact of GB on vortex motion in YBa2Cu3O7 conductors

Specifically,taking the superconductor YBa2Cu3O7(YBCO)as an example,we investigated the effect of GB on vortex motion in the superconductor.In calculation,the essential parameterαp/αvis set as 5.0×10−2,which is reasonable for YBCO samples.[26]As a result,the average moving velocities of vortices in the transverse and longitudinal directions versus the driving force were respectively plot in Fig.5.As shown in Fig.5(a),all the transverse velocities vxin three cases of different GB angles present similar a parabolic variation with a maximum value.But for different GB angles,generally,the transverse velocity vxpresents slightly different variations:with the driving force,the whole curve of the transverse velocity vxgradually shifting to the right,and the larger the GB angle is,the higher the maximum vxis.Generally,to a large extent,the transverse vortex motion is restricted by the strength of the GB potentials.The transverse velocity vxincreases with driving force at first,but when the component force in longitudinal direction reaches a strong enough value at which the vxrises up to its maximum,vortices launch across the grain boundary,which causes a decrease in the transverse velocity vx.

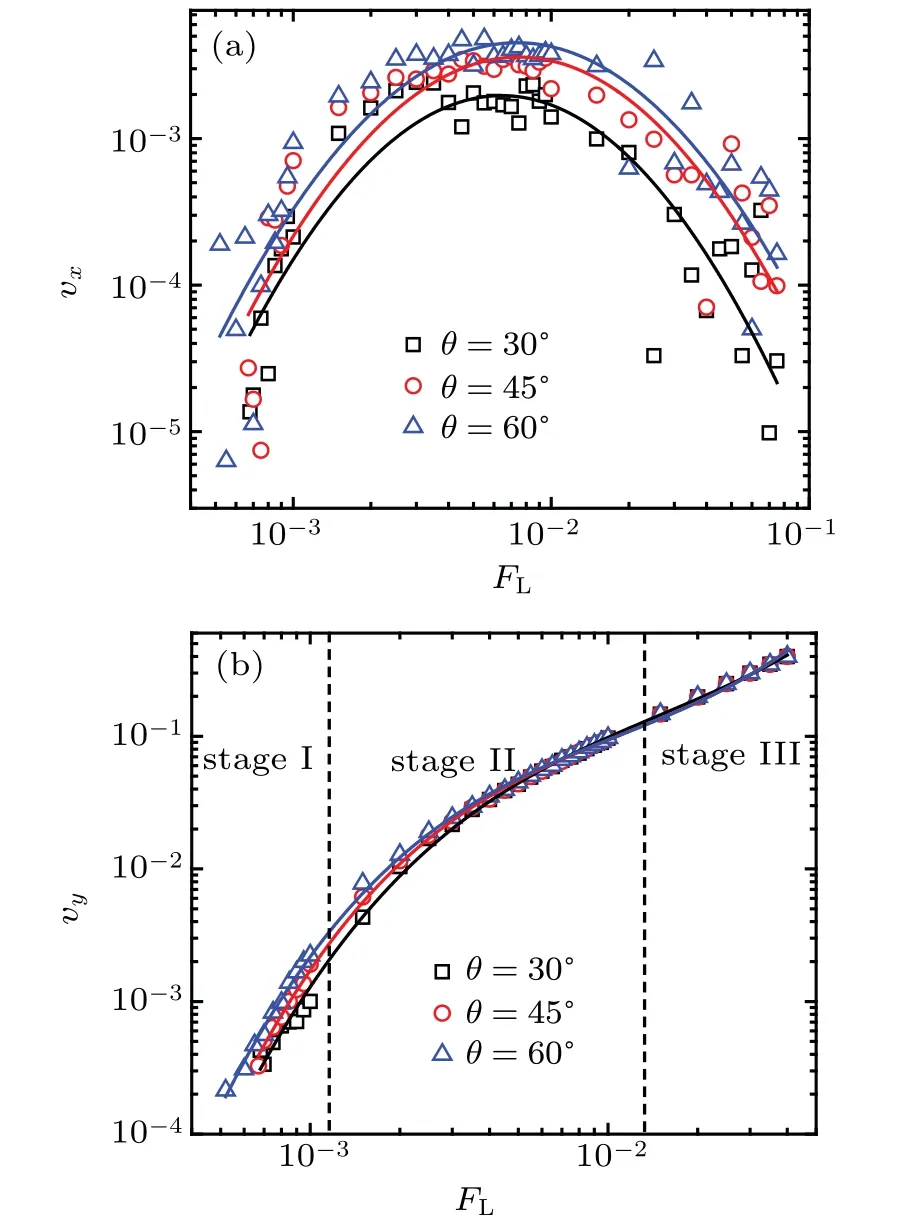
Fig.5.The average velocity(a)vx and(b)vy versus the driving force FL for the sample of size(Lx,Ly)= in three cases of different GB angles.

While the variation of the average velocity of vortices vywith the driving force is quite different.As shown in Fig.5(b),the velocity vymonotonically increases with the driving force for all three cases of GB angles.And in terms of magnitude,most of the velocity vy,as a whole,are one to two orders greater than the transverse velocity vx,and the velocities vyfor the two cases of the GB angle 60°and 45°,are close to each other,and slightly larger than that for the case of the GB angle 30°.Actually,more results show that the velocities vyincrease with the GB angle growing,and reaches maximum value at the angle reaching 90°,which corresponding to the moving direction of vortices parallel to the grain boundary.The results just indicate that the GB acts as easy flow channels for vortices moving parallel to the GB.More significantly,to deeply investigate vortex dynamics,on the calculated results we demonstrated three typical trajectories of vortices as shown in Fig.7,which is just matched up with three featured stages in Fig.5(b).In order to make the relationship between the GB and the trajectories more intuitive,the sample is revolved to the position where its edge parallel to the orientation of the applied current as the GB fixed(shown in Fig.6).The transformed sample still respect the original periodic boundary conditions.Here we try to make a complete illustration and in-depth discussion of the vortex dynamics in the YBCO sample with GB existing on the results of combined Figs.5(b)and 7.A channel occurs along the GB or in the vicinity of the GB when the driving force reaches the critical value(stage I).The vortices in the channel flow regularly past a series of fixed positions on the channel,viz.the trajectory of one given vortex on the channel fully displays the whole channel,as shown in stage I(Fig.7(b)).In this stage,the average velocities of vortices of the longitudinal component(i.e.,vy)presents an approximately linear increasing with the Lorentz driving force FL,which is shown as stage I in Fig.5(b).With FLincreasing,new channels which are generated as interconnected forms in the previous pinned area(stage II in Fig.7(c)).In this stage,the motion of vortices is somewhat disordered,which should be resulted from the average velocities of vortices nonlinearly increasing with the driving force in stage II shown in Fig.5(b).In stage III,the vortices flow orderly along the independent channels(Fig.7(d))as the driving force reaching to a sufficiently large value.And the average velocities of vortices for all three cases of the GB angles present an almost perfectly linear increasing with the driving force in stage III shown in Fig.5(b).

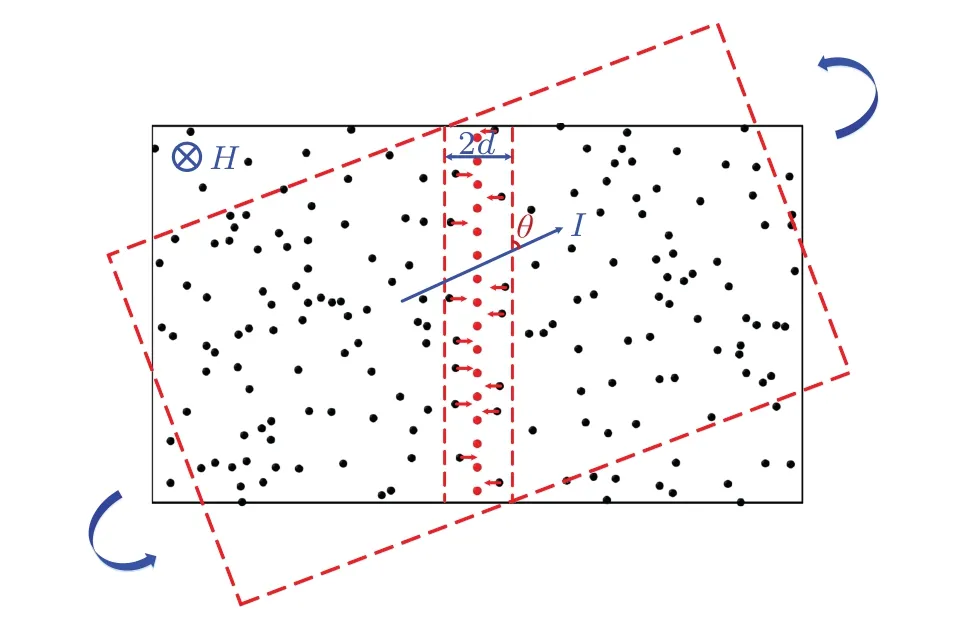
Fig.6.The sample revolved on the z axis to make the edge parallel to the direction of the applied current by fixing the GB.

Combining Figs.5 and 7,complete vortex motion in the area near GB should be understood as follows.The vortices begin to move firstly occurring in the vicinity of the GB,then with the Lorentz force growing,more interconnected moving channels are formed in the second stage,and finally all the vortices flow steadily.When the driving force gets strong enough,the vortices are able to cross through the GB,which causes a decrease in the transverse velocity.

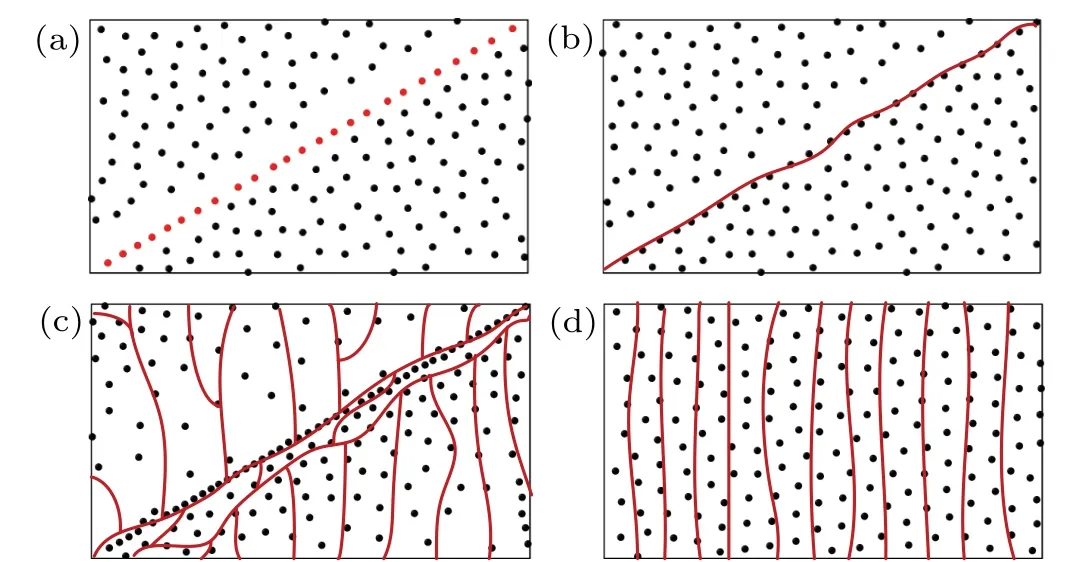
Fig.7.Typical trajectories of vortices in the YBCO sample with the GB of θ=30°during the three vortex movement stages:(a)the position of GB,(b)a channel along the GB(stage I),(c)interconnected channels formed(stage II),and(d)decoupled channels(stage III).

Besides the vortex dynamics,the resulted in macro transport properties of type-II superconductors should be much more concerned.Therefore,we furthermore investigate how the GB acts on the properties correlated to the transport current.For a type-II superconductor in the mixed state,the flux lines are subjected to the Lorentz force if the superconductor carries a transport current.If the vortices are driven by this Lorentz force with the velocity v,the electric field induced is as follows:

where B is the macroscopic magnetic flux density,and can be usually written as

whereφ0is the magnetic flux quantum and S is the area of the sample surface.N is the number of flux lines penetrating the superconductor sample.The Lorentz force acting on the flux lines can be calculated by

where J is the external current density.The practical critical current density is determined by the flux pinning in superconductors,fundamentally,and it is not an essential attribute,but depends on the flux pining,specifically the type,density,and configuration of pinning centers.According to Eqs.(6)–(8),the current–voltage characteristic of the YBCO superconductor with grain boundaries of various angles just corresponds to the relationship of the Lorentz force FLversus the velocityv.Thus,to reveal the current–voltage characteristic,we calculated the average velocity vyversus the driving force FLin the three cases of different magnetic field densities ranging from 0.025 T to 0.2 T for the GB angle 30°,which can be used for observing corresponding diverse characteristics of I–V curves.As shown in Fig.8,with the Lorentz force FLincreasing,the average velocity vyincreases slowly in the beginning,and then grows up gradually.Under smaller magnetic field,the vortices are more difficult to unpin and enter the flow state and match with lower average velocity.Particularly,several obvious fluctuations occur in the curve for the case of the smallest magnetic field intensity as 0.025 T,and this finding is nearly identical with the experiment observation.[26]This interesting phenomenon actually reflects the fact of the special feature of vortex dynamics in this case.As an intrinsic behavior for lower vortex densities which is proportional to the magnitude of the applied field,the strong fluctuations as well as sharp jumps are considered resulting from the melting transition of vortex lattice in high-Tcsuperconductors.[32]

Fig.8.The average velocity vy versus the driving force FL for the YBCO sample with the GB ofθ=30°under three cases of different magnetic fields.

4.Summary

In this article,we have studied the effect of GBs on vortex motion in type-II superconductors through molecular dynamical modeling.The most significant finding is that the role of GB on vortex motion can be changeable,in other words,it can transform between the two roles of strong barrier and easyflow channel.And the role change is intrinsically determined by the competition effect that the GB action on vortex motion is resulted from the two aspects:the internal GB strength in GB region and the external effect intensity(which can be characterized by the relative disorder strengthαp/αv)in no GB region.In conclusion,it is such the competition mechanism that determines the role of GB on vortex dynamics and transition between strong barrier or easy-flow channel.

For a superconductor YBCO sample with GBs,on molecular dynamical model and through the simulation of the depinning transition of vortices,we found three typical dynamical regimes and exhibited corresponding motion trajectories of vortices.The simulated results clearly revealed the role changing of GB on vortex motion and dominated by the competition effect between the GB and no-GB regions,which depends on essential characteristics of the grain boundary strength,angleθ,and the relative disorder strengthαp/αv.Further,we obtained the relation of the average velocity vyof vortices with their driving force FL,which is physically corresponding to the macroscopic current–voltage characteristics of YBCO conductors.Practically,in order to obtain a complete understanding of vortex motion in type-II superconductors,constructing the model containing multigrain boundary network is very necessary,and further relative studies are more significant for controlling artificial nanostructured pining defects,especially in coated conductors.