Chirp-dependent ionization of hydrogen atoms in the presence of super-intense laser pulses∗

Fengzheng Zhu(朱风筝),Xiaoyu Liu(刘晓煜),Yue Guo(郭月),Ningyue Wang(王宁月),Liguang Jiao(焦利光),and Aihua Liu(刘爱华),‡

1Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China

2School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China

3College of Physics,Jilin University,Changchun 130012,China

Keywords:ultrafast laser field,single photon ionization,quantum interference

1.Introduction

The invention of laser[1]has brought the modern science to a new era.With the development of the light source of this new type for six decades,the laser pulse of a few femtoseconds is easily produced in laboratories.[2–5]Such short laser pulse can be applied to the observation and control of the internal atomic and molecular dynamics.[6–9]The attosecond pulses might even be used to detect the electronic dynamics inside an atom.

As the optical device can generate dispersion modulation to the laser field,a chirp,which will make instantaneous frequency and phase change to the laser pulse,could be introduced during the generation of laser field.The chirped laser pulse has found a wide application in researches.For example,the chirped pulse can be used to explore the laser–matter interaction.[10–15]Especially,with the application of chirped pulse amplification(CPA)technique,[16]the intensity of laser can be dramatically increased.

Nowadays,free electron laser(FEL)light sources can generate a super-intense laser with peak intensity in the order of 1023–1024W/cm2.[17]For the light–matter interaction with such high peak intensity,there are many unexpected new physics and phenomena.For example,the atomic stabilization effect[18]would appear in the ionization process when a laser pulse with a peak intensity at around of 1016W/cm2or above is applied.Another example is the dynamic interference which has been predicted by many physicists recently.[19–21]

Interference process,which can be achieved by the double-slit scenario,is a vital wave phenomenon.Interestingly,one would expect to find the interference of the photoelectron wave packets produced in the ionization of atomic and molecular system in the presence of a super-intense and ultrafast laser field.The interference observed in the photoelectron spectrum is interpreted as a double-slit scenario in time-domain,as this kind of interference is formed by the electrons launched at different times,that is,one is on the rising part of the laser pulse and another one is on the falling part of the laser pulse.Moreover,owing to the notable ac Stark effect[22]involved in this process,such interference is referred as dynamic interference.[19,20,23]In addition,the atomic stabilization effect,which is closely related to the laser peak intensity,plays an important role in the formation of the coherent electron wave packets produced at different time.

The dynamic interference of ground state hydrogen atoms has been investigated extensively.[19–21,24–28]By solving fulldimensional time-dependent Schr¨odinger equation(TDSE),Guo et al.[21]and Jiang et al.[20]have discussed and confirmed the existence of dynamic interference within dipole approximation.Beyond the dipole approximation,Wang et al.[27]have investigated the corrections of non-dipole effects on the dynamic interference and confirmed the existence of dynamic interference in the photoelectron momentum distributions.In the works mentioned above,a non-chirped laser pulse is used.In order to investigate what changes in the dynamic interference can be taken by using a chirped laser pulse,we carry out the following work.

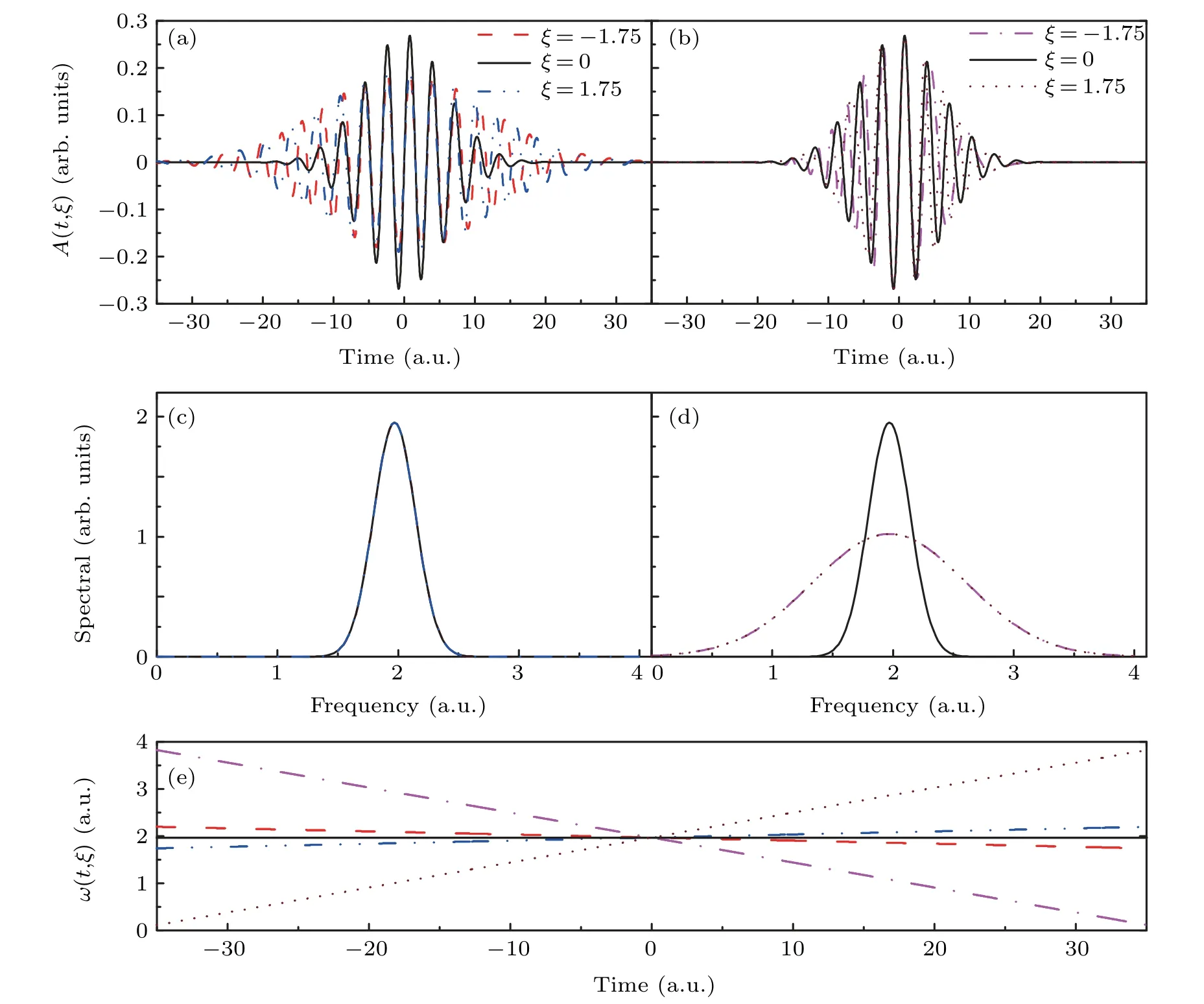
Fig.1.Schematics for the vector potential,power spectra profile,and instantaneous frequency for laser field with a central frequencyω0=53.6 eV and pulse durationτ0=0.24 fs at different chirp characters.Graphs(a)and(c)are presented for equal-power laser pulse which is labeled by form 1:solid dark line refer to results for non-chirped laser pulse withξ=0;blue dotted line is for the results for positive chirped laser pulse withξ=1.75;red dashed line is for the negative chirped laser pulse withξ=−1.75.Graphs(b)and(d)are presented for equal-FWHM laser pulses which are labeled by form 2:solid dark line refer to results for non-chirped laser pulse withξ=0;brown dotted lines are for the results for positive chirped laser pulse withξ=1.75;pink dash dotted lines are for the negative chirped laser pulse withξ=−1.75.Graph(e)presents the instantaneous laser frequencies for the above cases.

There are many different types of chirped pulses used in the experimental and theoretical studies,and those chirped laser pulse can be categorized into linear[28–34]and nonlinear chirped pulse.[35,36]Especially,two different expressions of the linear chirped pulse with Gaussian shape have been given by Tong et al.[29]and Barmaki et al.,[30]which have been used by experimental and theoretical physicists respectively.So,we intend to explore the effects of chirped pulse with different forms on the dynamic interference for the ionization of hydrogen atoms in the ground state.It is our aim to build a bridge between the results obtained from the experimental and theoretical physicists by discussing the similarity and difference for the results caused by those two pulse types.The vector potential of a linearly polarized chirped laser pulse can be written as

whereξis the chirped parameter.[37]In Fig.1,we present some properties for the chirped laser pulses of two forms which have been used in some literature.[29,30]The peak amplitude A0(ξ),instantaneous carrier frequencyω(t)and timedependent envelope F(t)are written as follows.The laser of first form can be expressed as[29](refer as form 1 in figures throughout this paper)

The laser for the second form can be written as[30](refer as form 2 in figures throughout this paper)

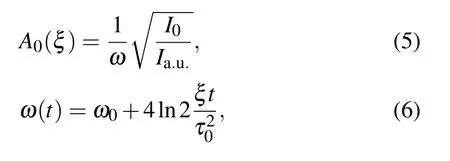
where Iau=3.51×1016W/cm2is the laser intensity of 1 a.u.

Here we will show an intuitive graphical representation of these two kinds of laser pulses in Fig.1,which includes the vector potential,power spectrum,and instantaneous frequency of non-chirped(ξ=0,dark solid line),positive-chirped(ξ=1.75,blue dash dotted line in Figs.1(a),1(c)and 1(e)and brown dotted line in Figs.1(b),1(d)and 1(e))and negativechirped pulses(ξ=−1.75,red dash line in Figs.1(a),1(c)and 1(e)and pink dash dotted line in Figs.1(b),1(d)and 1(e)),respectively.The laser fields are both supposed to take a central frequency asω0=53.6 eV and a pulse duration with τ0=0.24 fs.Figures 1(a)and 1(c)show some properties of the laser pulse which is described by Eq.(4)and named as form 1 pulse in our context.As illustrated in Fig.1(c),the energy spectra for the pulses with different chirped parameters present the same profile.Thus,pulse for the form 1 refers to equal-power pulse.It is preferred by experimental researchers[10,31,35]for it is easily obtained in laboratory.Another kind of laser pulse,which is described by Eqs.(5)–(7)and named as form 2 pulse in our context,are showed in Figs.1(b)and 1(d).As we can see that the pulses with different chirped parameters have the same full width at half maximum(FWHM)in Fig.1(b),i.e.,the amplitude of vector potential A0is independent of the chirped parameterξ.So,we also call it equal-FWHM form pulse.Theoretical researchers prefer to take pulse of this form as it is easy to describe.Comparing the vector potentials for the pulse in two forms shown in Figs.1(a)and 1(b),the pulse duration for the laser pulse of form 1 is longer than that for the pulse in form 2.But,from the view of energy spectrum which are represented in Figs.1(c)and 1(d),the width of the energy spectrum for the chirped laser pulse in form 2 is larger than that of chirped laser pulse in form 1.Besides,as displayed in Fig.1(e),the deviation of instantaneous frequency at time t/=0 for the equal-FWHM laser pulse is much larger than the one for the laser pulse of equal-power form.For example,at the end of propagation of the laser pulse,i.e.,t=τ0,the equal-power laser pulse has a deviation from the central frequency 53.6 eV with only 1.7 eV,while the equal-FWHM laser pulse gets a deviation up to 13.8 eV.Considering that the kinetic energy of the photoelectron is dependent on the frequency of the laser pulse,we expect to find some difference between the results obtained from our theoretial results for the ionization by the two different laser pulses.

The structure of the paper is as follows.In Section 2,we will outline the theoretical method about numerically solving the TDSE which describes the interaction between the hydrogen atom and the chirped laser pulse.The instantaneous ionization rate will be presented in following,and the dynamic interference observed in the photoelectron spectral will be discussed in Section 3.We will make a brief summary in Section 4.

Atomic units(¯h=e=me=1)are used throughout the paper unless otherwise stated.

2.Theory

An ab initio numerical framework is briefly presented in this section.In velocity gauge,the one-dimensional TDSE of hydrogen atoms in the presence of a linearly polarized ultrafast pulses can be given by

In Fig.2,we give the photoelectron energy spectra of(a)3D and(b)1D simulations.The 3D simulated spectrum agrees with the previous results with dipole approximation.[27]By comparing the 3D and 1D spectra,we can find that they are very similar in the interference pattern.Comparing with the 1D spectrum,the 3D spectrum has side peaks with a relative weaker signal.Such difference is probably due to the fact that the wave function must be expressed in a three-dimensional space for 3D simulation,but it is impossible for 1D simulation.

The electric field E(t)of a ultrafast pulse can be obtained from the first derivative of the vector potential versus time Then,after substituting the Hamiltonian into Eq.(8)and splitting the Hamiltonian into H=T/2+V+T/2,the wave function can be solved by

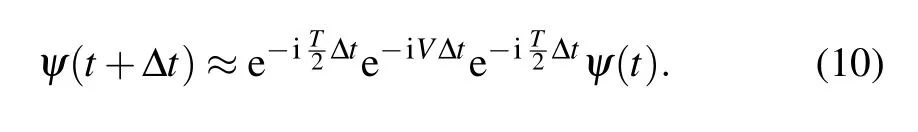
The initial stateψ(t=0)is obtained by replacing the real time t in TDSE by the imaginary timeτ=it.We obtain the final state after 5 fs free propagation at the end of laser pulses,and then apply the Fourier transform of the wave function to obtain the energy spectra of photoelectrons.

To separate the bound and continue wave functions,we need to project out the bounds states.We adopt mask function as following.When the wave function completes the final step of time propagation,we record the ionization part as[1−M(r)]ψ(x;tf).Hereψ(x;tf)is the wave function at the last time step.The function expression M(r)for absorption mask is[38]

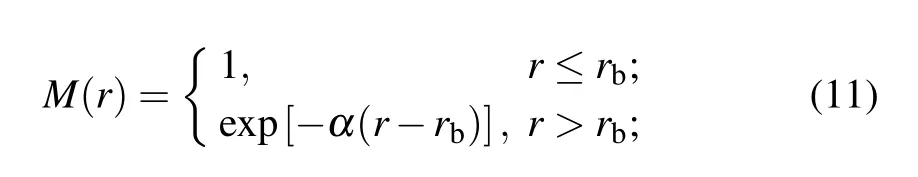
whereα=1,r=|x|,and rb=30.

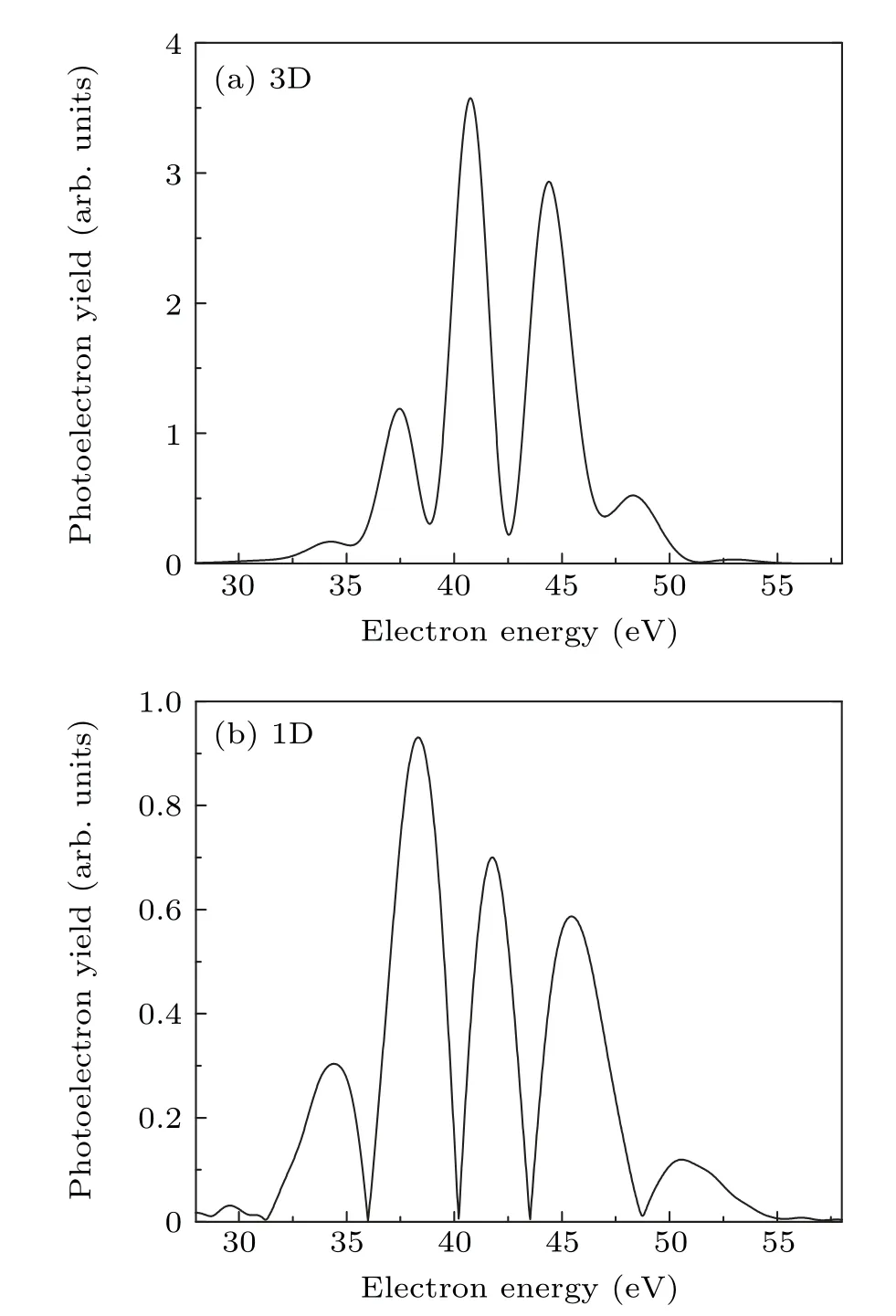
Fig.2.The photoelectron energy spectra of hydrogen atoms by(a)threedimensional(3D)and(b)one-dimensional(1D)simulation.Hydrogen atoms are in the presence of chirp-free laser pulses of pulse durationτ0=0.56 fs and central carrier frequencyω0=53.6 eV.The peak intensities are both 5×1018 W/cm2.

3.Results and discussion

In this section,we will discuss how the dynamic interference be affected by chirped pulses.As mentioned previously,the chirp parameters are chosen asξ=0,±1.75.The central carrier frequency of laser pulse is set to beω=53.605 eV in accordance with references,[18,20]and the pulse duration is taken to be 5 fs and 50 fs,respectively.In addition,we employ numerical grids with box side of 2000(forτ0=5 fs)and 20,000(forτ0=50 fs),respectively.In each optical cycle of laser pulse,there are 1024 time steps.These settings guarantee the convergence of the simulation in space and time intervals.

First,in Fig.3 we present the effect of the pulse intensity on the instantaneous ionization rates for the ionization of hydrogen atoms caused by a laser pulse of central photon energy 53.6 eV and pulse duration 5 fs.The instantaneous ionization rate is obtained from the integration of time dependent wavefunction probability density in momentum space with subtraction of bound states.In this figure,the left panel is for equalpower laser pulse,which is labeled by form 1,and the right panel is for equal-FWHM laser pulse,which is labeled as form 2,where the peak intensity is taken to be 1×1016W/cm2(a),(b),5×1017W/cm2(c),(d),and 3×1018W/cm2(e),(f),respectively.When the peak intensity of the laser pulse increases,the curve for the instantaneous ionization rate transforms from a single peak to double peaks both in the case of two different laser pulse.The depression between the peaks showed in Figs.3(e)and 3(f)means that no or little photoelectron is produced over the period in the middle of the laser pulse.It also indicates the atom stabilization arises in the ionization process when using a laser field with high intensity,and the photoelectrons are constituted by the wave packets produced before and after the atom stabilization process.Thus,a natural double-slit scenario in the time domain is established by the interference between the wave packets generated at different times.As one can see from Figs.3(a),3(c)and 3(e),when an equal-power laser pulse is used,the curves obtained by chirped laser pulse is non-coincident with the one caused by a non-chirped laser pulse.However,in each graph in Figs.3(b),3(d)and 3(f),for the ionization process in an equal-FWHM laser field,the instantaneous rates with different chirped parameters are almost the same in each figures.This means that the instantaneous rate for the ionization in an equal-power laser pulse is affected by the chirp parameter,whereas the one for an equal-FWHM laser field is independent with the chirp parameter.The difference mentioned above can be understood from expression for the envelope of vector potential.Since the interaction between the laser field and atoms is related to the vector potential of the laser pulse,the variation of ionization rate with time is similar to development of vector potential with time.Just as we can see from Figs.1(a)and 1(b)and Eqs.(4)–(7),the envelope of vector potential for the equal-power laser field includes a term of square of chirp parameterξ,but the one for the equal-FWHM laser field is independent ofξ.So,whether the instantaneous rate would be affected by the chirp parameter is different for the ionization generated by these two types of laser pulse.

Fig.3.The instantaneous photoelectron rate of hydrogen atoms in the presence of laser pulse with a central frequency ofω0=53.6 eV and pulse duration ofτ0=5 fs at three different laser intensities:(a),(b)I0=1×1016 W/cm2,(c),(d)I0=5×1017 W/cm2,and(e),(f)I0=3×1018 W/cm2.The left panel shows the results for laser pulse of form 1,and the right panel shows the results for laser of form 2.The dark solid line is for nonchirped laser field,the red dashed line is for negative chirped laser pulse with ξ=−1.75,and the blue dash-dotted line is for positive chirped laser pulse.

In addition,as indicated in Figs.3(e)and 3(f)where the separations between the two peaks plotted in colored lines are different,for the hydrogen atoms ionized by an equal-power laser pulse,the duration of atom stabilization is longer than that for the ionization caused by an equal-FWHM laser pulse.The difference attributes to the different envelope of vector potential between the two types of laser pulses.As we can see in Fig.1(a),the time span of the vector potential for a chirped laser field is longer than that for a non-chirped laser pulse.But for the equal-FWHM laser pulse showed in Fig.1(b),the vector potentials of different chirp parameters take the same time duration.Thus,compared with the birth time of the photoelectrons for the ionization in an equal-FWHM laser pulse,when a chirped equal-power laser filed is applied,the first photoelectronic wave packet is generated earlier and the second photoelectric wave packet is generated later.

Another obvious difference between two forms of chirp is that,the ionization rate curves of negative and positive chirps in equal-power form are almost the same,and curves of negative and positive chirps in equal-FWHM form are very different.These discrepancies can be understood by the instantaneous frequency of each forms which are shown in the Fig.1(e).In the equal-power case,the laser frequency varies much slower than that of equal-FWHM case,therefore,the negative and positive chirped pulses give birth to almost same instantaneous ionization rate profile.But for the equal-FWHM case,the negative and positive chirped pulses have greater discrepancies in their instantaneous laser frequencies.The positive chirped pulse has lower frequency in the raising half pulse than the negative chirped pulse,which allows it produce more photoelectrons(blue dotted-dashed line)than that of the negative chirped pulse(red-dashed curve)in the first half of laser pulse.In the second half of laser pulse,it is on the other case,and the red-dashed curve is stronger than the blue dotteddashed curve.

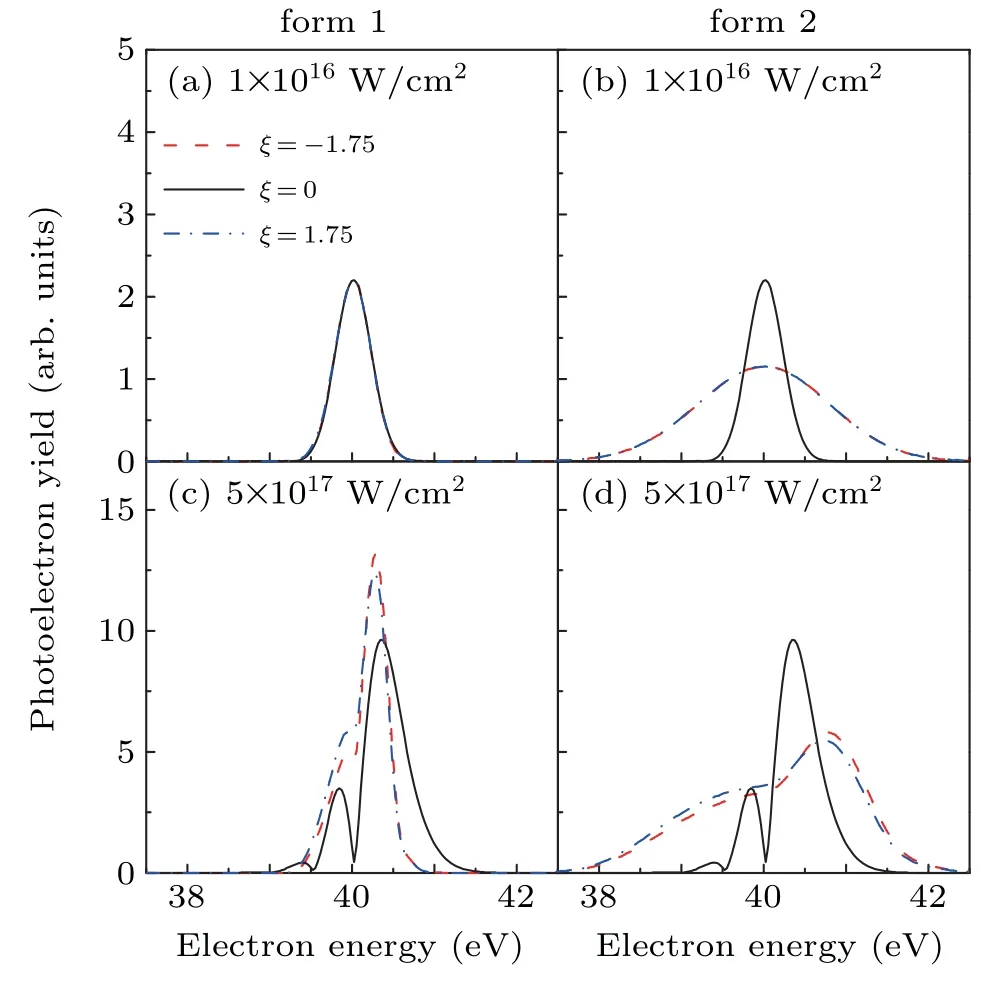
Fig.4.The energy spectra for photoelectron emitted from the hydrogen atoms irradiated by the laser pulse with a central frequency ofω0=53.6 eV and pulse duration ofτ0=5 fs at two different laser intensities:(a),(c)I0=1×1016 W/cm2 and(b),(d)I0=5×1017 W/cm2.The left panel shows the results for laser pulse of form 1,and the right panel shows the results for laser of form 2.The dark solid line is for non-chirped laser field,the red dashed line is for negative chirped laser pulse withξ=−1.75,and the blue dash-dotted line is for positive chirped laser pulse.

Figure 4 displays the energy spectra of the photoelectron ionized from the ground state hydrogen by the action of laser pulses of two different forms mentioned above respectively.We show the results of the photoelectron yield for equal-power(form 1)laser pulse in the left column(a),(c)and equal-FWHM(form 2)laser pulse in the right column(b),(d).In our calculations we use the laser pulse with central frequency asω0=53.6 eV,pulse duration asτ=5 fs,and peak intensity as 1×1016W/cm2(in Figs.4(a)and 4(b))and 5×1017W/cm2(in Figs.4(c)and 4(d))respectively.When the laser intensity is relatively low,as shown in Figs.4(a)and 4(b),the photoelectron spectra perfectly reproduce the shape of power spectra of each laser pulse shown in Figs.1(c)and 1(d).No dynamic interference exists for photoelectron with spectra of a single symmetrical peak.These results are in good agreement with the predictions obtained by perturbation theory.Once the laser intensity is increased to 5×1017W/cm2,the dynamic interference,which is illustrated by the spectrum with multiple peaks in Figs.4(c)and 4(d),occur for both the two forms laser pulse.Furthermore,by comparing the curve for non-chirped pulse with the curves for chirped pulses,no dynamic interference exists for the photoelectrons whose spectra has a single symmetrical peak.This can be understood from the photoelectron rate-time curves presented in Figs.3(c)and 3(d).For the ionization with such laser intensity,while none atomic stabilization can be found from the curves depicted for the chirped laser pulse,and an obvious atomic stabilization already arises for the non-chirped pulse,which corresponds to the widen and deformed shape of the peak plotted with black solid line.As we can see,the results from two different form laser pulses have something in common.Meanwhile,there are some differences between the spectra.When the peak intensity of the laser pulse is low,the power spectrum of the photoelectron emitted by equal-power laser pulse is irrelevant to the chirp parameterξ,but the power spectrum obtained by chirped equal-FWHM laser pulse(red dashed line and blue dash-dotted line in Fig.4(b))is a widen profile with a single peak.This kind of widen-shape influence for the photoelectron yield,which is produced by the equal-FWHM laser pulse originated from the broadening for the power spectrum of chirped laser field,is also presented for the ionization by a laser pulse with high intensity.As we increase the peak intensity to 5×1017W/cm2,for the case of ionization by an equal-power laser pulse,the power spectrum produced by chirped laser pulse have a higher peak with respect to the one obtained from non-chirped laser field.However,for the photoelectrons launched by equal-FWHM laser pulse,the comparison for the peaks of energy spectra is reversed.

Furthermore,in order to find the influence taken by the increase in pulse duration,in Fig.5,we present energy spectra of the photoelectrons emitted from the hydrogen atoms which are ionized by a laser field with pulse duration increased to 50fs.Comparing results shown in Figs.4(a),4(b),5(a)and 5(b)for the ionization realized by laser pulse in low intensity,we find that the energy spectra of photoelectron forτ0=50 fs take narrower distribution than those forτ0=5 fs.These changes are consistent with the change caused by the increased pulse duration in the energy spectrum of laser pulse.Once we use a laser pulse in high peak intensity,the number of oscillation in spectrum profile,in which the dynamic interference has been indicated,also increase with the extension of pulse duration.In addition,we also find that the performance of energy spectrum in which dynamic interference has appeared is related with chirp parameterξ.As we can see in Fig.5(c)referring to the case of equal-power laser pulse,the span of spectrum profile for the chirped laser pulse only covers the low energy region which is the part of the distribution of spectrum in nonchirped pulse.As illustrated in Fig.1(a),chirped laser field has a longer time span than the one for the non-chirped laser field.Therefore,comparing with the ionization generated by a non-chirped laser field,the atomic stabilization caused by a chirped laser pulse begins earlier on the raising edge of the pulse and ends later on the falling edge of the pulse.Thus,for the ionization by a chirped laser pulse,the time interval between the birth of coherent electron wave packet is longer and the width for the profile of energy spectrum is narrower.In Fig.5(d),for the case of equal-FWHM laser pulse in high intensity,we could find that:First,the photoelectrons generated by chirped and non-chirped laser pulse respectively,especially for the one emitted by non-chirped and negative chirped laser pulse,have same profile for the energy spectrum of high energy range.As Figs.3(d)and 3(f)show,the birth time of electron wave packets is independent with chirp parameter.Thus,the energy spectra for those photoelectrons,which are launched at the same moment in the equal-FWHM laser pulse of different chirp parameters,present same profiles.Second,the spectrum for a positive chirped laser pulse reaches to a maximum which is lager than the maximum in the spectra for the non-chirped and negative chirped laser pulse.Since the instantaneous frequency of chirped pulses has large deviation from the central frequency,the instantaneous frequency of the positive chirped laser pulse in the raising edge belongs to a region with energy below the central frequency.Thus,the photoelectrons are emitted with low kinetic energy by the application of laser field of such low instantaneous frequency.Finally,we get an energy spectrum represented in Fig.5(d)in which the yield for photoelectron created by positive chirped laser field is higher than the one generated by non-chirped or negative chirped laser field.In addition,comparing the energy spectral profiles in the region of high energy,we can see that the highest yield is obtained by using a negative chirped laser field.The reason for this is that the instantaneous frequency of negative chirp laser field in the raising edge of the pulse possesses a positive deviation.

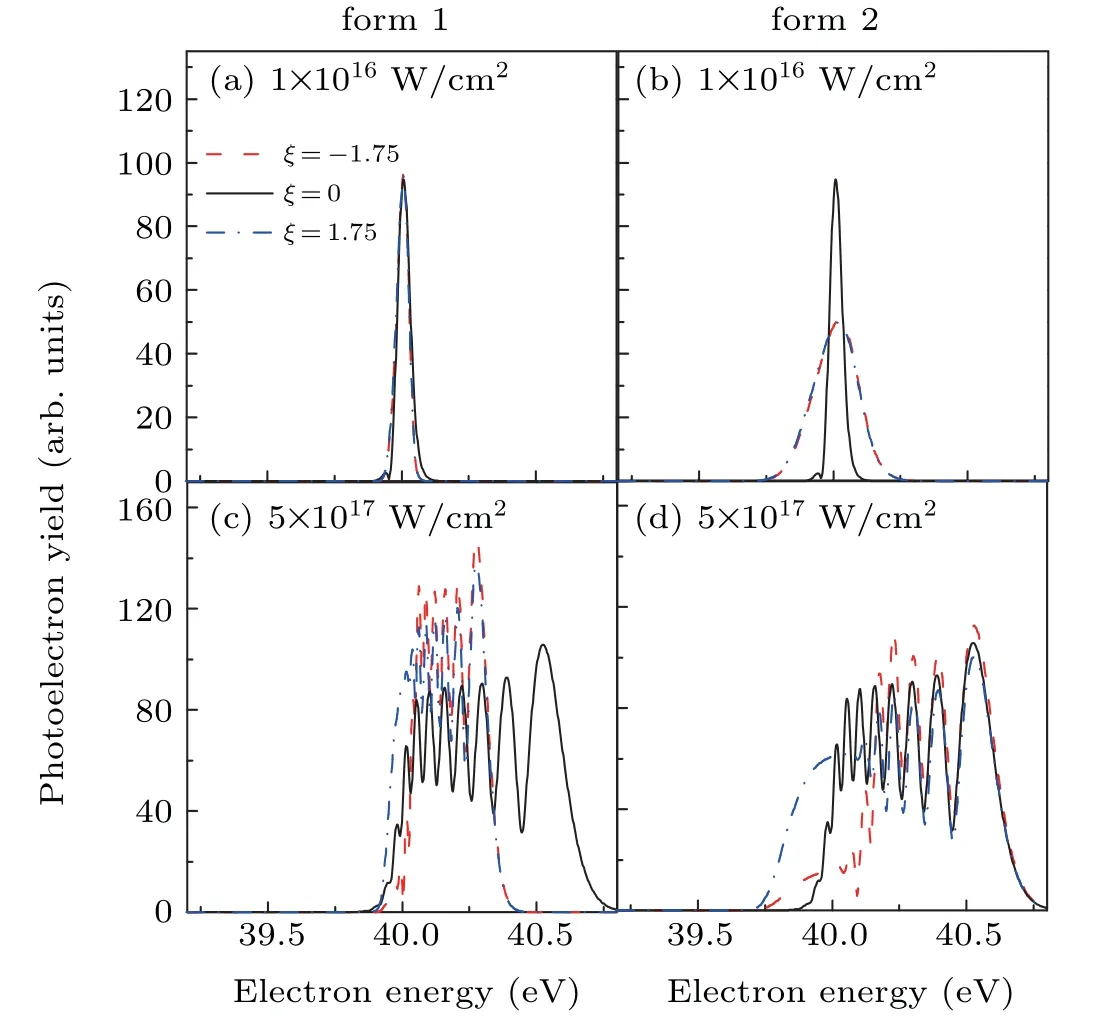
Fig.5.The energy spectra for photoelectron emitted from the hydrogen atoms irradiated by the laser pulse with a central frequency ofω0=53.6 eV and pulse duration ofτ0=50 fs at two different laser intensities:(a),(c)I0=1×1016 W/cm2 and(b),(d)I0=5×1017 W/cm2.The left panel shows the results for laser pulse of form 1,and the right panel shows the results for laser of form 2.The dark solid line is for non-chirped laser field,the red dashed line is for negative chirped laser pulse withξ=−1.75,and the blue dash-dotted line is for positive chirped laser pulse.

4.Conclusion

To reveal the influence of super-intense chirped laser pulse on the atomic ionization process,we have explored the dynamic interference of photoelectron generated in the ionization of ground state hydrogen atoms in the presence of super-intense ultrashort laser pulse,using the time-dependent Schr¨odinger equation.Hoping to build a bridge between the experimental and theoretical researches,an equal-power laser pulse and an equal-FWHM laser pulse were both considered in our studies,where non-chirped,positive chirped and negative chirped laser pulses were taken into account.With an increasing peak intensity of laser pulse,the time evolving of photoelectron yield transforms from a single peak to double peaks,from which the atomic stabilization induced by a high intensity laser field has been confirmed.Then a corresponding dynamic interference of photoelectron wave packets has been observed in the energy spectrum,and comparison between these results induced by the two different laser pulse has been made.For the case of short laser duration,no matter which form of laser pulse was used,the dynamic interference fringes created by non-chirped pulse are more clearly to be made out than the one induced by chirped laser pulse.However,the change of peak value in the energy spectrum,which is brought by the transformation from non-chirped laser pulse to chirped laser pulse,is opposite when these two laser field of different form are applied separately.Once we increase the pulse duration,the dynamic interference is more noticeable with the increasing fringes in the energy spectrum.Our results showed that the distribution of energy spectrum for the photoelectron generated by chirped laser pulse is narrower than the one produced by non-chirped laser pulse.While the energy spectrum of photoelectron is spread in low energy region for the case of equal-power laser field,the photoelectrons emitted by the equal-FWHM laser field prefer to have high energy.

Acknowledgement

Part of the numerical simulation was done on the high performance computing cluster Tiger@IAMP in Jilin University.