Dynamic modeling and aperiodically intermittent strategy for adaptive finite-time synchronization control of the multi-weighted complex transportation networks with multiple delays∗
2021-09-28NingLi李宁HaiyiSun孙海义XinJing靖新andZhongtangChen陈仲堂
Ning Li(李宁),Haiyi Sun(孙海义),Xin Jing(靖新),and Zhongtang Chen(陈仲堂)
1College of Sciences,Northeastern University,Shenyang,China
2College of Science,Shenyang JianZhu University,Shenyang,China
Keywords:complex transportation networks,adaptive finite-time synchronization,multiple delays and multiweighted,aperiodically intermittent control
1.Introduction
Cyber physical systems(CPS),as the unity of computing process and physical process,are the next generation of intelligent system integrating computing,communication and control.CPS realizes the interaction with the physical process through the man–machine interaction interface,and uses the networked space to manipulate a physical entity in a remote,reliable,real-time,safe and cooperative way.[1]Compared with the Internet of things,CPS puts more emphasis on control.CPS has been concerned by many research institutions and scholars since it was first proposed in 2005.[2]In recent years,CPS has become a hot research direction and a lot of achievements have been made in priority industrial field for enterprises.[3]CPS has been widely used in intelligent transportation,aerospace,smart power grid,disaster early warning,military exercise,logistics and supply chain optimization and so on.The research and application of CPS are of great strategic significance for accelerating the integration of industrialization and informatization.[4–6]
Complex dynamical network is an important method to describe and study the complex systems.According to different research aspects,many complex systems can be abstracted into a complex network of interacting individuals from the practical background.Over the past 20 years,the complex dynamical networks have been the focus of attention,and have gained more and more attention in various fields.Many scientific and technical systems can be modeled as the complex dynamical networks.[7–10]
The emergence of CPS brings about new opportunities for the researchers in the field of network,which gives rise to cooperative control of multiple robots,attitude control of multiple satellites,formation control of unmanned aerial vehicle,smart grid control,intelligent transportation system,and so on.[11,12]The outstanding characteristic of CPS is an intelligent network composed of many devices with communication,computing and decision control functions.It can make the whole system in the best state through interaction.The operation of CPS is actually a collection of information transmission,synchronization,optimization,control and other dynamic processes in the complex dynamic networks.[13]
There are rich dynamic behaviors in the analysis of complex network.Synchronization is one of the most important dynamic behaviors of the complex network.[14]Common phenomena in life,such as the resonance phenomenon,the cricket chorus,the flock of birds,and the rhythmic applause broke forth the audience in the theatre are widely known as synchronous phenomenon.Many practical problems are closely related to synchronization,such as the synchronous phenomena on the communications networks,the transportation networks,the human connection networks and WWW.[15–19]The synchronous study of complex networks is around the relationship and the network structure among the network behaviors.The research on synchronization control of complex networks is helpful to understand the influence of network structure on synchronization of complex systems,which can supplement the synchronization analysis of complex networks.[20–22]In the study of synchronous control of complex networks,many control methods have been introduced,such as adaptive control,[22,23]pinning control,[24,25]intermittent control,[26,27]finite-time control,[27–31]and sampled-data control.[32]
The collaborative scheduling control of the transportation network can be taken as an example of the CPS system.[11,33]In the control of multiple means of transportation,different means of transportation are required to arrive at the same place at the same time as possible.In the complex transportation networks,when the air transportation,rail transportation,road transportation and water transportation are synchronized over a period of time,the time of goods staying in the logistics center can be reduced,the empty load rate of the transportation tools can be reduced,the average time of inventory can be shortened,and sometimes even the time of inventory in the logistics warehouse center can be eliminated.Therefore,it is necessary to conduct in-depth research on the synchronization of complex transportation networks,which will provide important theoretical support for the construction planning of macro-regional logistics and the auxiliary decision-making of transport line distribution and dispatch in the future.
On the other hand,in the complex transportation networks,delay is inevitable due to the limited speed of transmission and traffic congestion.After considerable development,many complex network models that can reflect the actual characteristics have been established.In actual transportation network,sometimes the physical distance among nodes is far.The speed of vehicles,carrying capacity of transportation routes,transit and storage effect of logistics are limited.References[34,35]introduce the idea of network splitting,and establish a multi-delay complex network model.This network can be well applied to complex transportation networks with multiple delays.However,the weights of different nodes in each subnetwork are not reflected.Wang et al.[36]have made some attempts at splitting the weights.Wang put forward a complex network model based on weight by using the idea of network splitting and introducing the concept of weight.The model is analyzed synchronously and the pinning controller is designed.But the delays of different nodes in each subnetwork are not considered.In Ref.[37],the model of complex networks with multi-delay and multi-weight is preliminarily established.A simple linear feedback controller is designed using the technique of linear matrix inequalities.There is some conservatism in the controller design.Therefore,how to build a complex network model that can comprehensively reflect the delay and weight should be further studied.
The occurrence of delay often affects the performance of the system,resulting in the vibration and even instability of the complex transportation network.There have been many research results on synchronization in delays complex networks.[38,39]Especially,how to solve the finite-time synchronization problem of the complex transportation networks with multiple delays and multi-weighted is still challenging.
Based on the results of the above discussion and the idea of CPS,we proposed the model of multi-weighted complex transportation networks with multiple delays.On the basis of the theory of Lyapunov stability,the technique of adaptive control,aperiodically intermittent strategy and finite-time control,the adaptive aperiodically intermittent finite-time synchronization controllers have been designed.The external coupled configuration matrices do not require to be irreducibility and symmetry.Finally,the correctness and effectiveness of the proposed controllers are verified by the numerical simulations.
The remainder of this paper is organized as follows.In Section 2,based on the ideas of CPS and network splitting,the multi-weighted complex transportation network model with multiple coupling delays is established,and some necessary assumptions and lemmas are given.In Section 3,the adaptive aperiodically intermittent finite-time synchronization of the multi-weighted complex transportation networks with multiple delays is researched via the theory of Lyapunov stability,the technique of adaptive control and finite-time.The adaptive aperiodically intermittent finite-time synchronization controllers are designed.The numerical simulation results are given to illustrate the theorems in Section 4.Finally,the conclusion is drawn in Section 5.
2.Model description and preliminaries
Transportation systems can be well described by complex network models.Each region involved in transport can be used as a node in the complex transport network system.And each mode of transportation(such as air,rail,road,water,and pipeline)connecting any two regions can be abstracted to represent each side of a complex network.[37]In order to make the model better reflect the structural properties of the actual system,it is considered that the same network can be split many times,that is,the subnetwork obtained by the first split is regarded as a complete network,and then the subnetwork is split to a more detailed split result.We fully consider delay and weight in modeling and further improve the model in this paper.First of all,different types of transportation models have different transport velocity.As the transportation velocity of the highway network,railway network,navigation network and aviation network are different,under the premise of simultaneous departure,the velocity of aviation network is the fastest,and the railway network,highway network and navigation network have a time lag of arrival time for the aviation network,respectively.Therefore,the idea of network splitting can describe the multi-delay complex transportation network system.Second,for the same traffic mode,each subnetwork is divided again according to the weight attribute of the path and station in the road network.And the weight division is to divide nodes and edges according to their weights in the network.The practical significance of its division is to divide the stations and lines in the traffic network according to their busy degree in the network.Therefore,based on the idea of network splitting and CPS,the N coupling nonlinear and diffusion of the multi-weighted complex transportation networks with multiple delays model,with each node as an n-dimensional nonlinear system is described as follows:
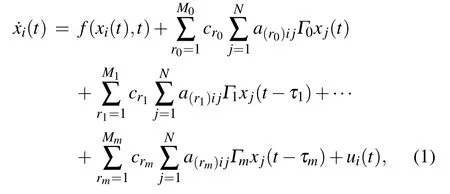
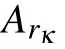
Remark 1The model(1)is very useful for understanding the multi-weighted complex transportation networkmodel with multiple coupling delays.In the real world,many practical systems can be abstracted by the model(1),such as biological networks,and communication networks.The model(1)is a synthesis and generalization of many other models.For example,when M0=M1=···=Mm=1,the model(1)is degenerated to the complex network model with multiple delays in Refs.[34,35].Whenτ1=τ2=···=τm=0,the model(1)is degenerated to the multi-weighted complex networks in Ref.[36].Moreover,the following results do not have to satisfy the conditions in the past of outer coupling configuration matrices to be symmetric or irreducible.
When the states x1(t)→···→xN(t)→s(t),as t→T∗,the multi-weighted complex transportation networks model with multiple delays(1)realizes finite-time synchronization.Where s(t)∈Rnis the solution of an isolated node,i.e.,


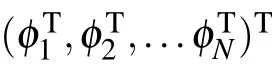
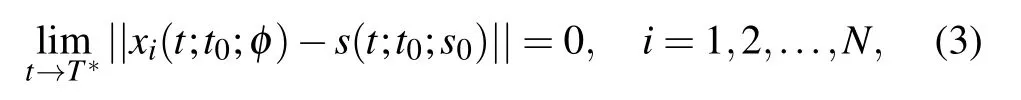
where s(t;t0;s0)is a solution of the system(2)with s0∈Rn,then the multi-weighted complex transportation networks model with multiple delays(1)is said to realize finite-time synchronization,andΛ×Λ×···×Λis called the region of finite-time synchrony of the multi-weighted complex transportation networks model with multiple delays(1).
In order to reach the following conclusions,we give the following necessary assumptions and lemmas.
Assumption 1There exists positive constant Li(i=1,2,...,N).f:Rn×R→Rnis a nonlinear vector-valued continuous function,which satisfies the Lipschiz condition
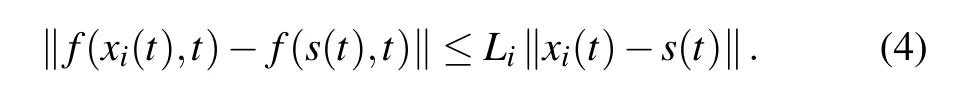
Lemma 1[27]Suppose that function V(t)is continuous and non-negative when t∈[−τ,+∞)and satisfies the following conditions:
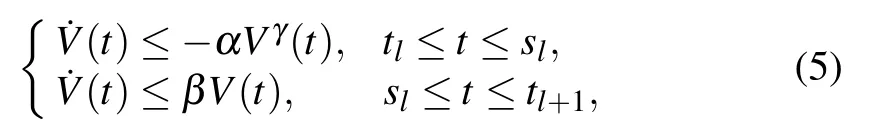
where l=0,1,2,...,α,β>0,0<γ<1.If there exists a constantψ∈(0,1),whereψis defined as follows:
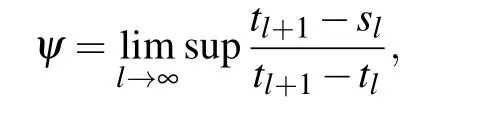
then the following inequality holds:
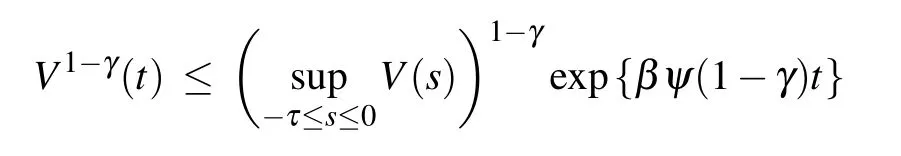
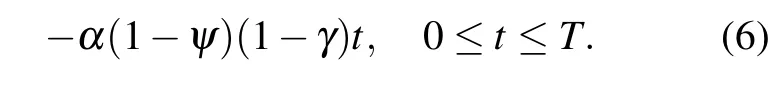
where the constant T is the settling time.
Remark 2Lemma 1 plays an important role in the intermittent finite-time synchronization analysis and control of complex networks via periodically intermittent control.In the Lemma 1,tl+1−tlis the length of the lth aperiodical control period.tl+1−sland sl−tlrepresent the non-control time and control time in the l-th control period respectively.
Lemma 2[40]For any n dimensional column vectors x,y,positive definite n×n dimensional matrix Q,the following matrix inequality holds:

If not specified,inequality Q>0(Q<0,Q≥0,Q≤0)means Q is a positive(or negative,or semi-positive,or semi-negative)definite matrix.
Lemma 3[41]Letξ1,ξ2,...,ξnare positive numbers and 0≤µ1<µ2,then
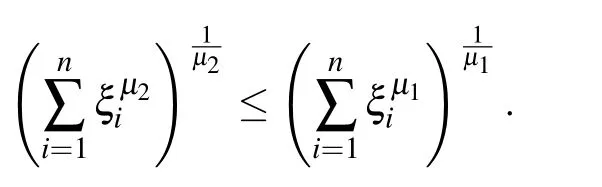
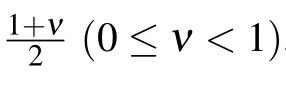
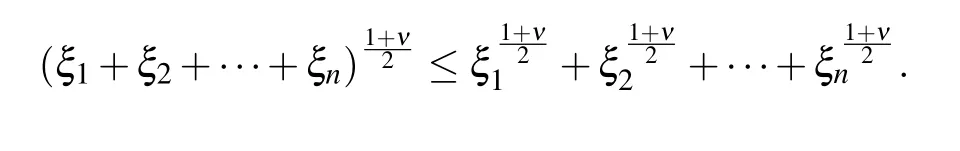
3.Aperiodically intermittent strategy for adaptive finite-time synchronization control of the multi-weighted complex transportation networks with multiple delays
For the convenience of proof,we defnie the error vector as follows:
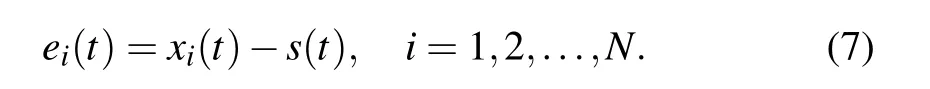
Then the error system corresponding to model(1)is can be described by
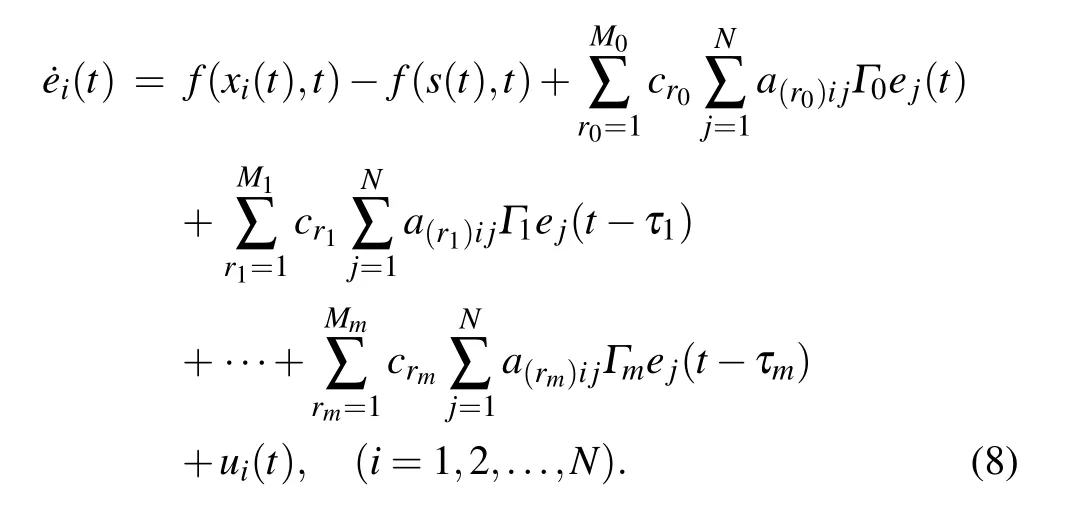
When the error dynamical system(8)achieves finite-time stabilization,the multi-weighted complex transportation networks with multiple delays(1)realize finite-time synchronization.
In order to enable the multi-weighted complex transportation networks with multiple delays(1)finite-time synchronization,we design the following aperiodically intermittent adaptive finite-time controllers:
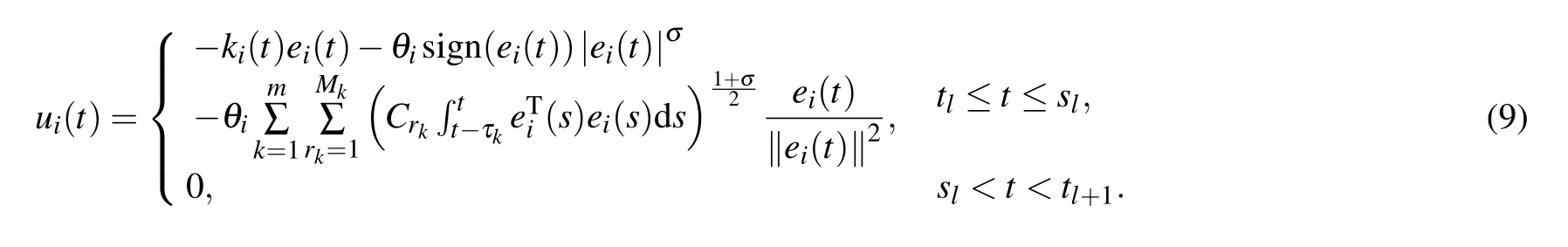
and updating laws
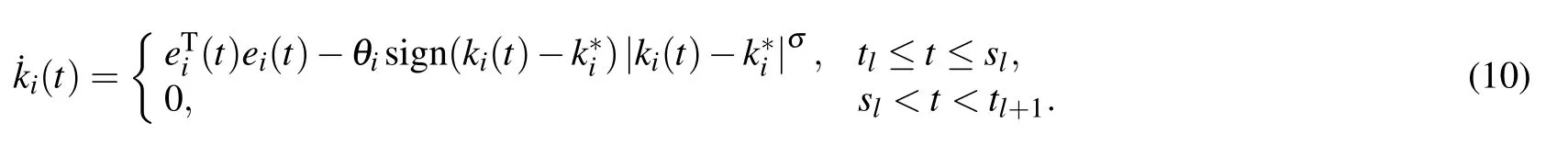
Using the theory of stability theory,the technique of adaptive control,aperiodically intermittent control and finite-time control theory,the synchronization controller of the multiweighted complex transportation networks with multiple delays(1)under the aperiodically intermittent adaptive finitetime synchronization controllers(9)and(10)can be got as following.
Theorem 1If the Assumption 1 holds,there exist positive constantsψ∈(0,1)and positive definite matrixΦdefined as follows,such that the following inequality holds:
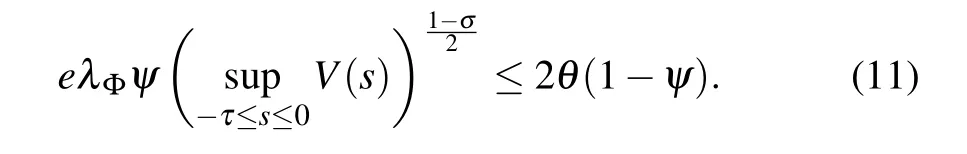


By Lemma 2,the subsequent inequation holds:
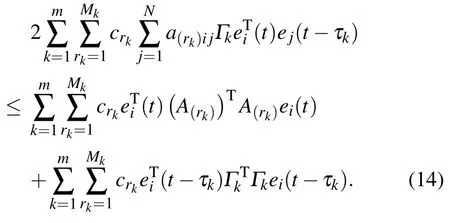
Combining with the Assumption 1,and substituting inequality(14)into Eq.(13),we can get


Because0≤σ≤1,based on Lemma 3,it is easy to obtain the following inequality:

and we have
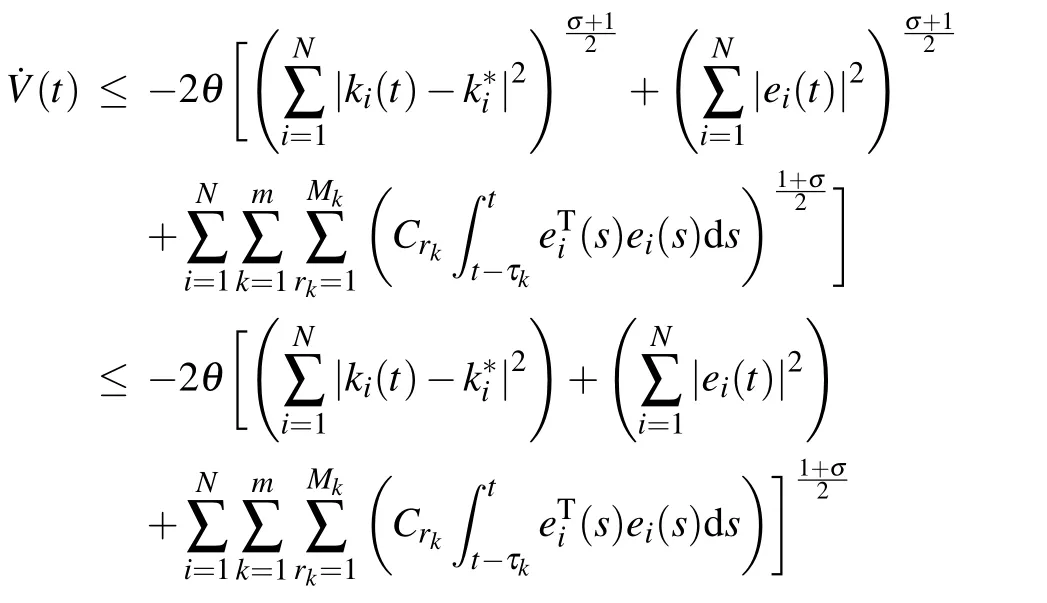

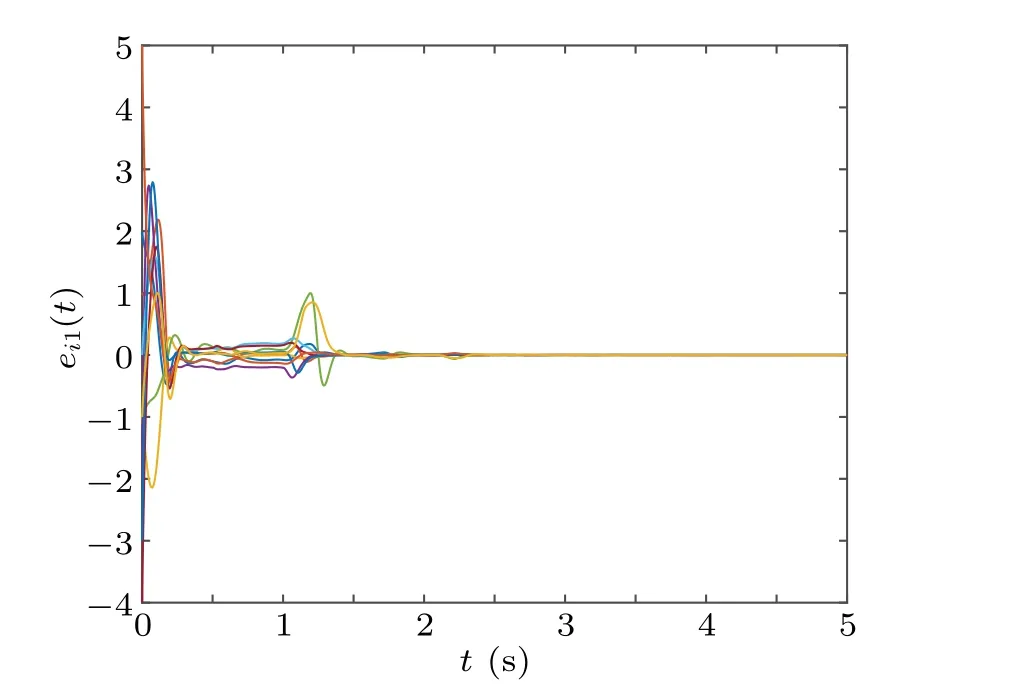
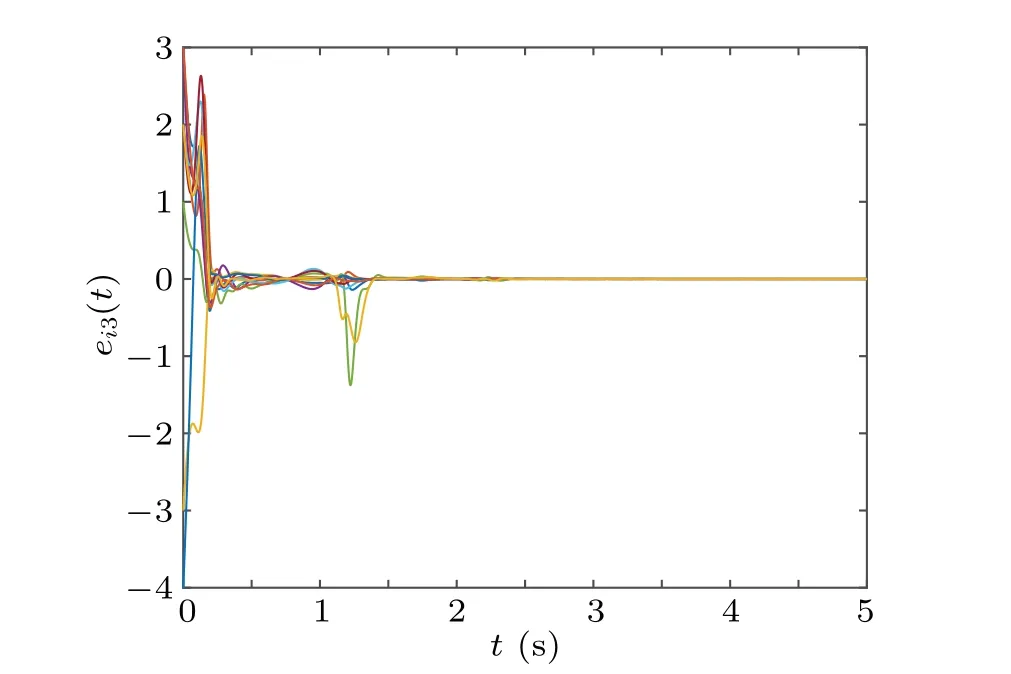
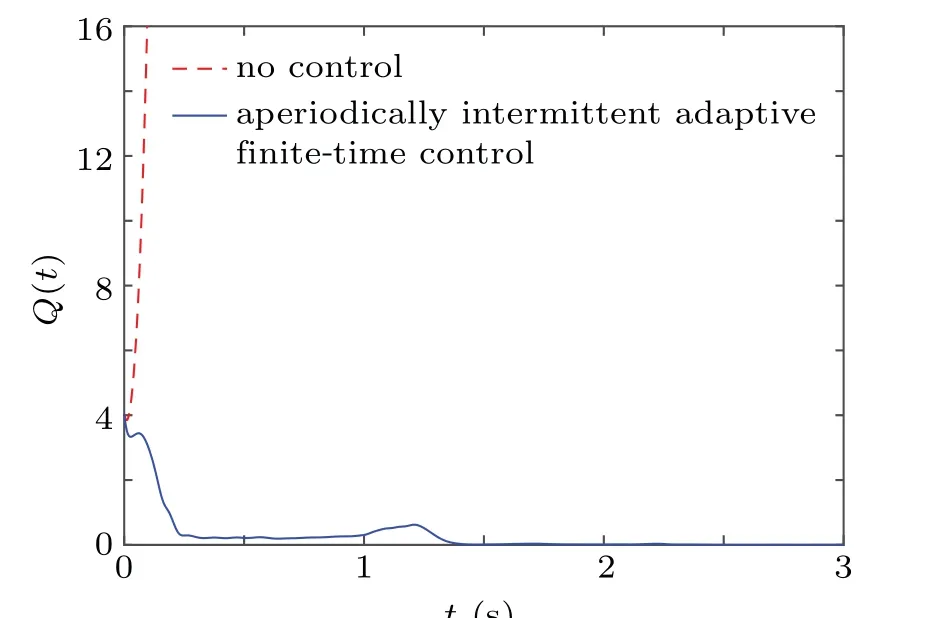
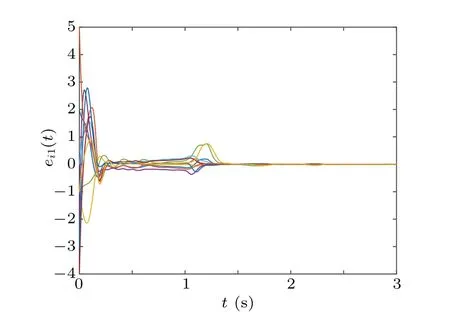
Similarly,when sl So we can derive the following result: i.e., Next,we give the value of finite-time T∗.Apparently,T∗satisfies the following equation: Take the derivative of both sides of the Eq.(23)with respect to t,and properly arrange it to obtain Substituting Eq.(24)back into Eq.(23),we can get Then we apply condition(25)to discuss the value of finitetime T∗. The proof is completed. Remark 3If tl+1−tl=T and tl+1−sl=δ(l=0,1,2,...),where T andδare positive constants,the aperiodically adaptive intermittent finite-time control strategy becomes the adaptive periodic intermittent finite-time control strategy.Therefore,the control strategy we designed is more general and more flexible to use.And we also give the condition for finite-time synchronization and the specific time T∗of finitetime synchronization. Remark 4In the complex networks(1),when M0=M1=···=Mm=1,the multi-weighted complex transportation networks with multiple delays(1)is degenerated to the following form: Equation(26)is the complex networks with multiple delays of Ref.[34]We take the same aperiodically intermittent adaptive finite-time controllers(9)and updating laws(10)to get the following corollary. Corollary 1If the Assumption 1 holds,there exist positive constantsψ∈(0,1)and positive definite matrixΩdefined as follows,such that the following inequality holds: Remark 5In the complex networks(1),whenτ1=τ2=···=τm=0,the multi-weighted complex transportation networks with multiple delays(1)is degenerated to the following form: Equation(28)is the complex networks with multi-weighted of Ref.[36].Accordingly,we design the aperiodically intermittent adaptive finite-time controllers as follows: Then we select the following Lyapunov–Krasovskii function: Corollary 2If the Assumption 1 holds,there exist positive constantsψ∈(0,1)and positive definite matrixΔdefined as follows,such that the following inequality holds: To verify the validity of the proposed theorem in the section III,we give the numerical example. Example 1In this example,we choose 10 cities as the nodes of the complex transportation networks.Air transportation,railway transportation and highway transportation are three modes of transportation in complex transportation network.According to the level of the city and the busy degree of a certain vehicle,the weight is divided into three orders of magnitude.We abstract it as the complex transportation networks with 3-weighted and 2 coupling delays,which can be described as follows: Chen system as the single node of dynamical equationf(·)is described as follows: When the parameters a=35,b=−7,c=28d=−3,the Chen system has a chaotic attractor.Similar to Ref.[25],there exists L=5.5619 that makes Assumption 1 hold. In this simulation,the initial values of states xi(0)(i=1,2,...,5)are given at random.s(0)=(1,1,1)T,ki(0)=1 andθi=5(i=1,2,...,10),σ=1/4,θ=6.The aperiodically intermittent control period is randomly assigned to the interval.[1,2]The control time is randomly assigned to[0.5,1.5].ThenΨ=1/4. It can be obtained by verification that all the conditions of Theorem 1 are satisfied.Applying Theorem 1,the multiweighted complex transportation networks with multiple delays(33)can be synchronized by applying the following aperiodically intermittent adaptive finite-time controllers(9)and the update laws(10)with a finite time T∗=2.88. Fig.1.Synchronization errors ei1(t)of network(33)under the aperiodically intermittent adaptive finite-time controllers(9)–(10). Fig.2.Synchronization errors ei2(t)of network(33)under the aperiodically intermittent adaptive finite-time controllers(9)–(10). Fig.3.Synchronization errors ei3(t)of network(33)under the aperiodically intermittent adaptive finite-time controllers(9)–(10). Figures 1–3 show the synchronization errors of ei1(t),ei2(t),ei3(t)with aperiodically intermittent adaptive finitetime controllers(9)–(10).It is obvious that the synchronous errors of network(33)with adaptive feedback controller(9)under the updating laws(10)converge to zero after a short period of time.Because this paper uses intermittent control,the error system is not immediately asymptotically stable.During the period of time that is not controlled,the system response curve may oscillate slightly and gradually stabilize,as shown in Figs.1–3,from 1 second to 1.5 seconds,the error increases and then converges to zero.When the air transportation,railway transportation and road transportation reach the synchronization after a period of time,it can reduce the time of goods staying in the logistics center,reduce the empty rate of transport vehicles,and shorten the average inventory time. All other parameters are the same as Eq.(33).We plot the synchronization quality Q(t)in the Fig.4. Fig.4.The qualities Q(t)with the disturbance signal under the aperiodically intermittent adaptive finite-time controllers. Fig.5.Synchronization errors ei1(t)of network(33)with the disturbance signal under the aperiodically intermittent adaptive finite-time controllers(9)–(10). Fig.6.Synchronization errors ei2(t)of network(33)with the disturbance signal under the aperiodically intermittent adaptive finite-time controllers(9)–(10). Fig.7.Synchronization errors ei3(t)of network(33)with the disturbance signal under the aperiodically intermittent adaptive finite-time controllers(9)–(10). Obviously,the synchronization quality Q(t)can not achieve synchronization without controller.The state of the error system diverges rapidly without controller,while the aperiodically intermittent adaptive finite-time controllers(9)–(10)can still guarantee the synchronization of the controlled network(33).It is shown that the aperiodically intermittent adaptive finite-time controllers have strong robustness against uncertainties. In this paper,we have researched the adaptive finite-time synchronization of the multi-weighted complex transportation networks with multiple delays via aperiodically intermittent strategy based on the CPS.Using the technique of adaptive control,finite-time control,aperiodically intermittent control and the theory of Lyapunov stability,we design the adaptive aperiodically intermittent finite-time synchronization controllers.The controllers we designed are very useful for understanding the finite-time synchronization in the multi-weighted complex transportation networks with multiple delays.When the coupling strength or structure changes,the aperiodically intermittent adaptive finite-time controller designed still has strong robustness.Moreover,there is no requirement for the outer coupling configuration matrices to be irreducible or symmetric.Finally,the effectiveness of the adaptive aperiodically intermittent finite-time synchronization controllers is verified by numerical example.It shows that the controllers designed in this paper have correctness and effectiveness.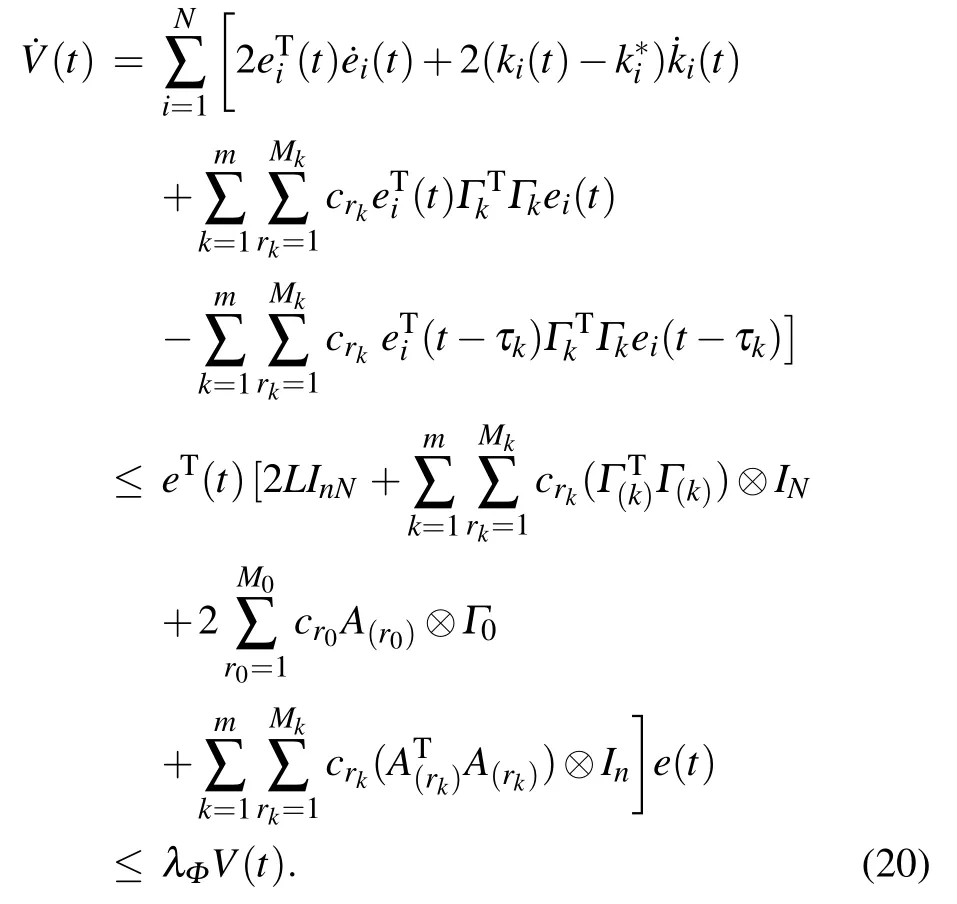

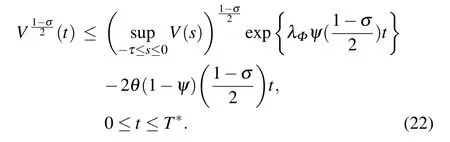

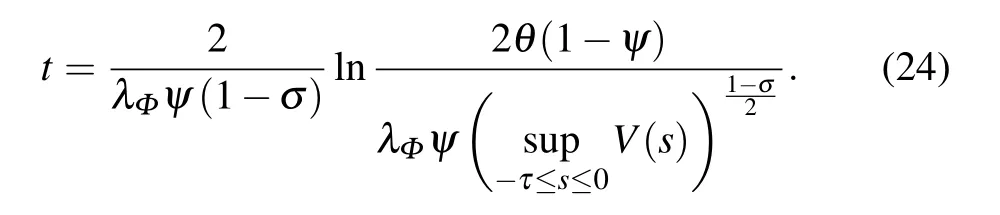
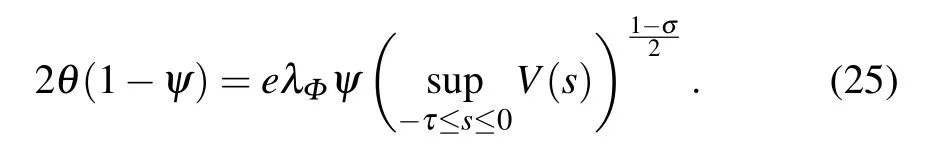

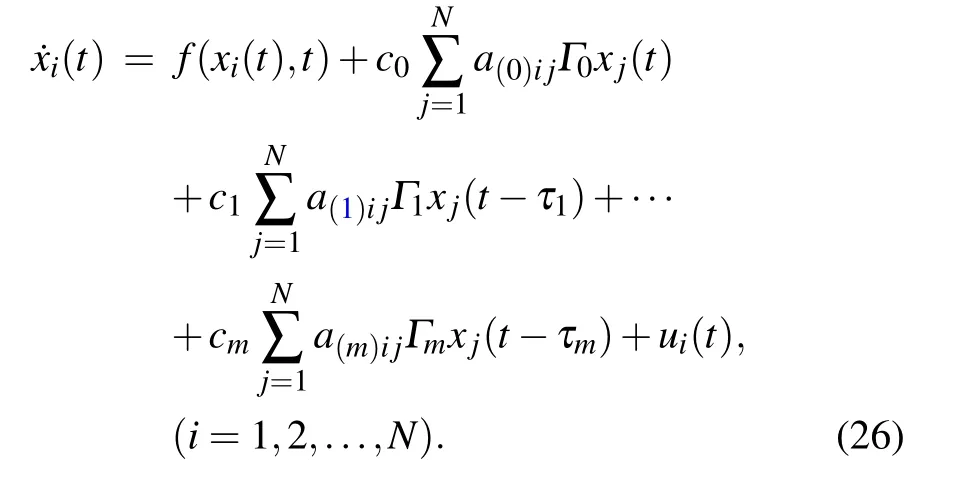



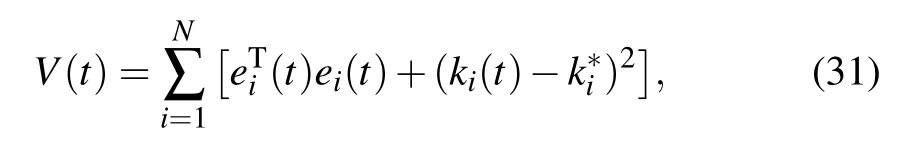

4.Numerical simulation
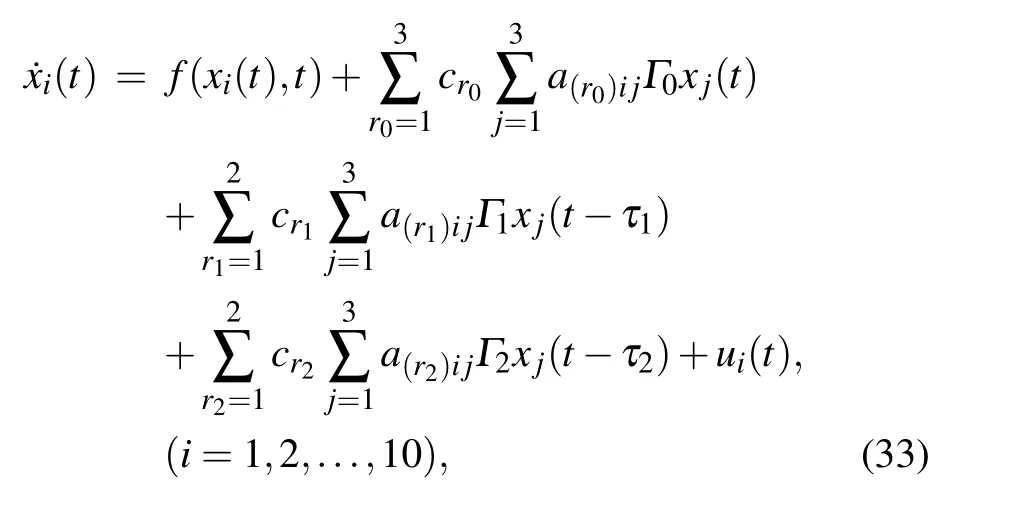
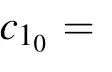

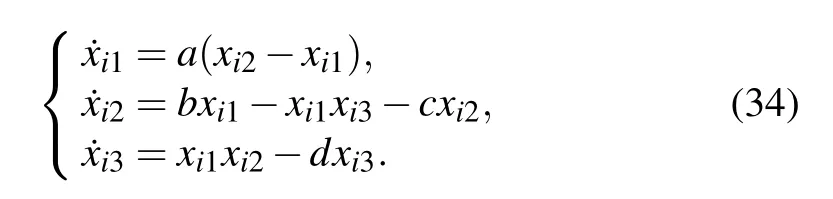





5.Conclusion
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Origin of anomalous enhancement of the absorption coefficient in a PN junction∗
- Protection of isolated and active regions in AlGaN/GaN HEMTs using selective laser annealing∗
- First-principles study of plasmons in doped graphene nanostructures∗
- Probing thermal properties of vanadium dioxide thin films by time-domain thermoreflectance without metal film∗
- An improved model of damage depth of shock-melted metal in microspall under triangular wave loading∗
- Signal-to-noise ratio of Raman signal measured by multichannel detectors∗
