An optimized cluster density matrix embedding theory

Hao Geng(耿浩)and Quan-lin Jie(揭泉林)

Department of Physics,Wuhan University,Wuhan 430072,China

Keywords:cluster density matrix embedding theory,distant correlation,Heisenberg J1–J2 model

1.Introduction

Distant correlations capture interesting physical properties(for example,phase transitions[1–9]in exotic phases)of the quantum spin system,which is a typical strongly correlated quantum many body system.But as the dimension of the Hilbert space grows exponentially with the system size,it is difficult to solve a large system exactly.An effective and accurate description of large systems would have significant impact on theoretical predictions.Density matrix embedding theory(DMET)[10–14]is a cheap method to map the system to a quantum impurity plus bath problem.The complexity,of the impurity basis construction in DMET,could amount to a rather small matrix diagonalization.However,the DMET still needs remarkable computational cost to simulate large systems,because it needs different configurations to formulate the system.

In this paper,we optimize the cluster density matrix embedding theory(CDMET).[13]In our optimized CDMET,the configurations,of a great part of the system,are treated as identical.This reduces the computational cost.The accuracy is the same as before.The new CDMET we propose in this paper is effective and computationally accessible.It does not deteriorate with the system size.It can be applied to a broad range of problems.We study the validity of the new CDMET by implementing it on the Heisenberg J1–J2model on the square lattice.The Hamiltonian of this model is

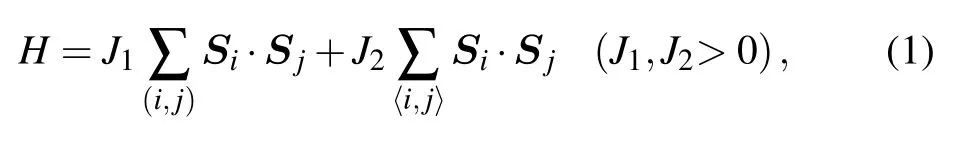
where(i,j)represents the nearest neighbor(NN)and〈i,j〉represents the next nearest neighbor(NNN).For convenience,we set J1=1 as the energy unit throughout the paper.We set the lattice spacing between the nearest neighbor spins as the length unit.We define a cluster as a square of 2×2 spins.This shape of cluster is demonstrated to be suitable for application to a square J1–J2lattice.[13]We consider the system with periodic boundary conditions.This model is simple and useful in Fe-based superconductors and other materials.[15]Different theoretical approaches are used to study this model.[13,14,16–29]A well-established consensus is that the model has Neel magnetic long range order at small J2region and stripe magnetic long range order at large J2region.The combined effect of frustration and quantum fluctuations destroys antiferromagnetism.It leads to a nonmagnetic quantum paramagnetic(disordered)phase(intermediate phase),within the intermediate parameter region.However,two problems of this model are still under debate:the nature of the disordered intermediate phase,and the phase transition between it and the Neel phase.Because of the sign problem,large scale quantum Monte Carlo simulations cannot be applied to these two problems.[30]We think that our new CDMET is a good alternative option to shed light on these two problems.In Refs.[13,14],the Neel phase(a long range order phase)appears at small J2values.At J2～0.42 the system transfers from the Neel phase into a disordered phase.The system undergoes a transition to the stripe phase(another long range order phase)at J2～0.62.We repeat their results with CDMET.

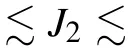
2.Formulation

The wave function of CDMET is[13]

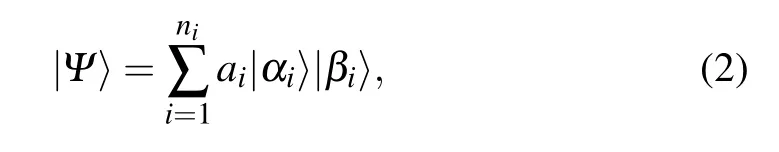
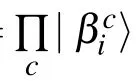
In the new CDMET,the neighbor clusters of the embedded spins are treated just like in the original CDMET.The distant clusters from the embedded spins are treated as shown in Eq.(3).This formulation simplifies the bath states.It is based on the consideration that the remote clusters have minor influence on the embedded spins.This treatment reduces the computational cost.It lightens the burden in the calculation of large systems.Fan et al.[13]noted that the spin energy of the remote clusters is close to that obtained by the hierarchical mean-field method.

The subsequential question is to decide which clusters should be treated as neighbor clusters in the new CDMET.To answer this question,we try some cases(Figs.1–3)with the new CDMET.We compare the spin energy of an embedded cluster obtained by the original CDMET with that obtained by the new CDMET.In the first case,the clusters(red solid boxes in Fig.1),which have both J1and J2interactions with the embedded spins,are treated as neighbor clusters in the new CDMET.In this case,the spin energy is close to the original result(Fig.2).The spin energy difference between the original and the new CDMET is not obvious at small J2values.But at large J2region,the difference becomes obvious.In the second case,the clusters(red dashed boxes in Fig.1),which have only J2interactions with the embedded spins,are treated as neighbor clusters in the new CDMET.In this case,the spin energy difference between the new and the original CDMET is obvious at all J2values(Fig.2).

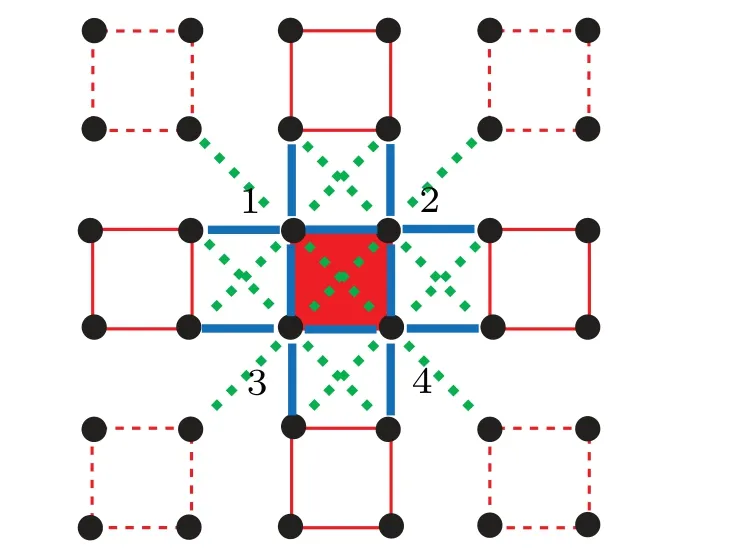
Fig.1.The black circle dots denote the spins.The blue(green dashed)bonds denote the nearest(next nearest)neighbor interactions.The red shaded box denotes the impurity cluster.The red solid boxes denote the bath clusters which have both J1 and J2 interactions with the impurity.The red dashed boxes denote the bath clusters which only have J2 interactions with the impurity.The embedded spins are numbered from 1 to 4.

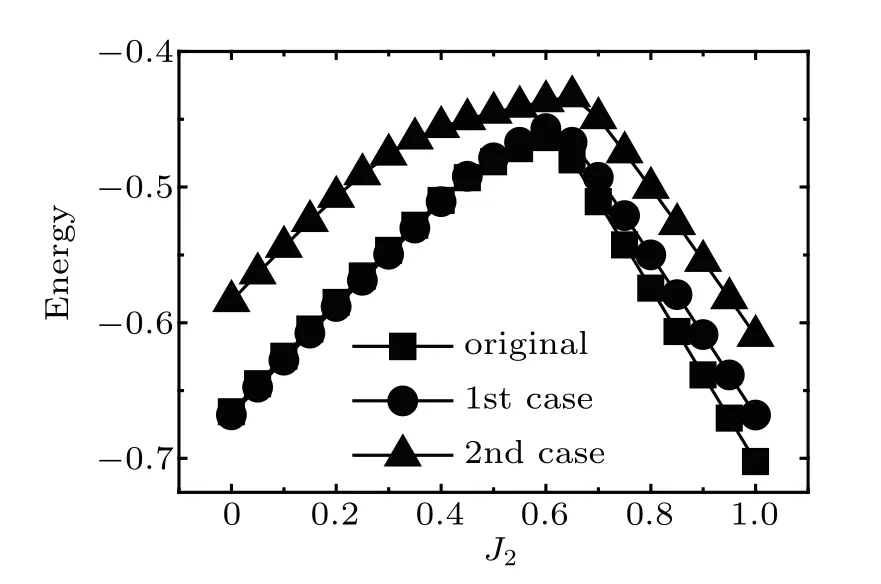
Fig.2.The spin energy of an embedded cluster,obtained by the original CDMET(squares)and the new CDMET,in a system of 8×8.Two cases in the new CDMET are considered.In the first case(cycles),the clusters,which have both J1 and J2 interactions with the embedded spins,are treated as neighbor clusters.In the second case(triangles),the clusters,which have only J2 interactions with the embedded spins,are treated as neighbor clusters.

In the third case,the clusters(red solid boxes and red dashed boxes in Fig.1),which have(J1,J2)interactions with the emebdded spins,are treated as neighbor clusters in the new CDMET.In this case(Fig.3),the spin energy obtained by the original CDMET is pretty well consistent with that obtained by the new CDMET.The original CDMET is implemented in the system of 8×8.The new CDMET is implemented in the systems of 8×8,12×12,24×24.The largest absolute value of the spin energy differences(Fig.3(b))between the new and the original CDMET is about 0.002.The error between different methods seems to be the largest around PVB to stripe phase transition in Fig.3.As it is a first order phase transition,the wave function has a sudden change.A disturbance may take place around this phase transition.This enlarges the error.Some curves in Fig.3(a)are shifted.Without shift,the curves in Fig.3(a)are completely identical.Meanwhile,in the system of 12×12,in the third case,to run a step(calculate all the states and all the clusters once),the new CDMET needs about 1/5–1/4 of the time needed by the original CDMET.Starting from a random initial wave function,we measure the time that the new(original)CDMET needs to get the ground state wave function.At a J2value,we try 15 random initial wave functions,and take the average time Tnew(Toriginal).The ratio Tnew/Toriginalat J2=0.2,0.45,0.55,0.80 are respectively about 0.16,0.25,0.22,0.29.This illustrates the gain in computational efficiency of the new CDMET.The new CDMET reduces the computational cost,and is as accurate as the original CDMET.Furthermore,the spin energies(Fig.3)obtained by the new CDMET implemented in different system sizes are consistent with each other very well.This indicates that,unlike some other simulation approaches,the new CDMET,as well as the original CDMET,[13]is insensitive to the system size.It can obtain reasonable results in the thermodynamics limit at a finite system size.This allows us to study the system at the thermodynamic limit without further extraneous numerical approximations.However,in the new CDMET,the lack of long-range interactions in the spin lattice model may be a reason for the insensitivity to the system size.

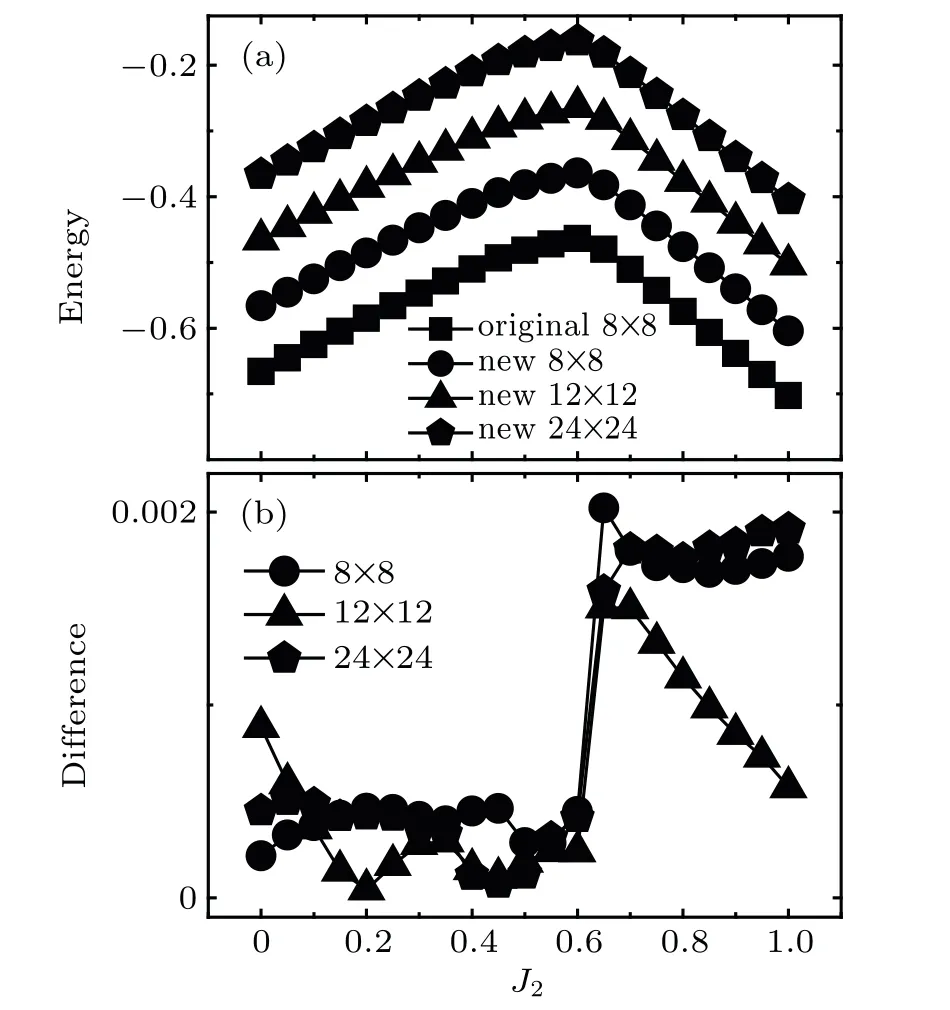
Fig.3.(a)The spin energy of an embedded cluster,obtained by the original and the new CDMET.The curves of cycles,triangles,pentagons are respectively shifted by 0.1,0.2,0.3.Without shift,the four curves are completely identical.(b)The absolute values of the spin energy difference between the original CDMET and the new CDMET.The original CDMET is implemented in the system of 8×8(squares).The new CDMET is implemented in the systems of 8×8(cycles),12×12(triangles),24×24(pentagons).

3.Distant correlation

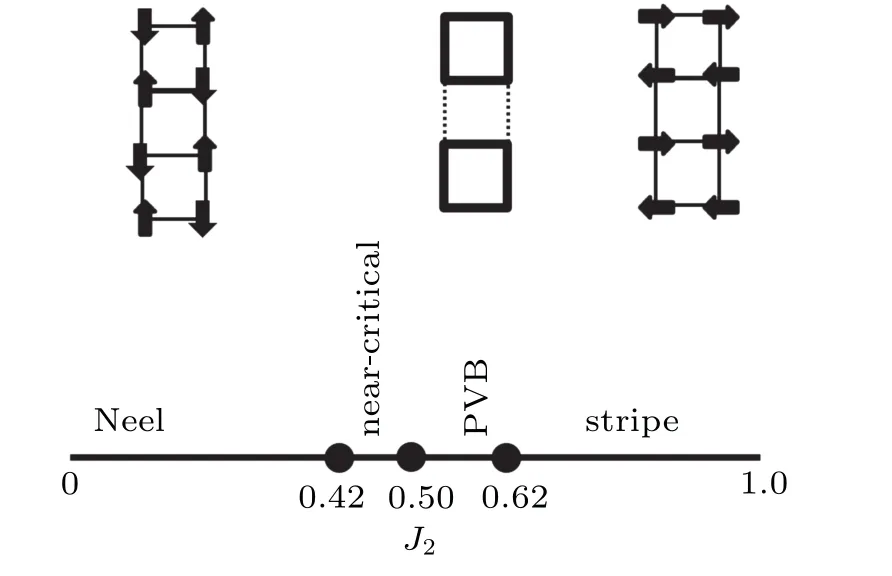
Fig.4.Ground state phase diagram of Heisenberg J1–J2 model on square lattice obtained in the present study.

3.1.The intermediate phase is divided into two parts

Fig.5.Absolute values of spin correlations obtained from the new CDMET in the system of 24×24.The blue diamonds denote the Neel phase.The black triangles denote the near-critical region.The red circles denote the PVB phase.The green pentagons denote the stripe phase.(a)From top to bottom,the curves respectively denote the spin correlations at J2=0.40,0.42,0.44,0.46,0.48,0.50,0.51,0.52,0.53,0.55,and are respectively shifted by 100.9,100.8,100.9,100.8,100.7,100.6,100.3,100.2,100.1,0.0.(b)Except for the curve of green stars,from bottom to top,the curves respectively denote the spin correlations at J2=0.58,0.60,0.62,0.64,0.66,0.68,0.70,and are respectively shifted by 100.2,100.4,100.6,0.0,100.1,100.2,100.3.

Moreover,the spin energy curves(Fig.3)also indicate that this phase transition is continuous.To support this,we calculate the entanglement entropy(EE)and its first order derivative in Fig.6.If we divide the system into two parts A and B,the EE between these two parts is defined as S=−Tr(ρAlog2ρA),whereρA=TrB(ρAB)is the reduced density matrix of part A.We embed a cluster.Part A is spin 1(squares in Fig.6);or spins 1,2(circles in Fig.6);or spins 1,2,3(triangles in Fig.6);or spins 1,2,3,4(diamonds in Fig.6)of the embedded cluster(Fig.1).Part B is the rest of the system.A discontinuity or singularity in the EE indicates a first order quantum phase transition,and a peak in the derivative of the EE indicates a continuous quantum phase transition.[13]All the derivatives of EE peak at J2≈0.42(Fig.6(b)).This indicates that the phase transition from the Neel phase to the intermediate phase is continuous.By contrast,the spin correlations have a sudden change in the transition from the PVB phase to the stripe phase(Fig.5(b)).This indicates that this phase transition is a first order one.This is also supported by the discontinuity or singularity of the EE(Fig.6(a)).

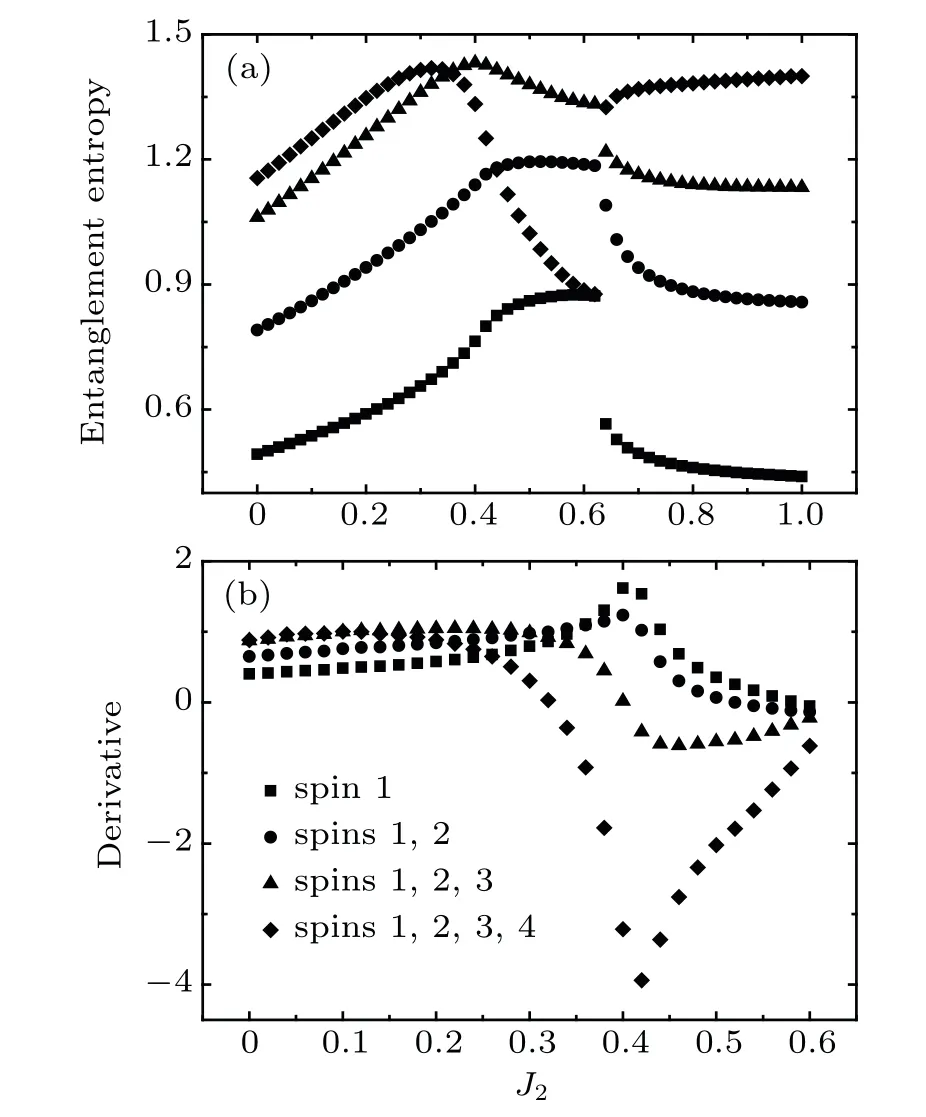
Fig.6.(a)Entanglement entropy(EE)and(b)its first order derivative on a system of 24×24.The squares,circles,triangles,diamonds respectively denote the EE(first order derivative of EE)of spin 1;spins 1,2;spins 1,2,3;spins 1,2,3,4 in the embedded cluster.

If we embed 6 spins at the top left corner of 6 horizontally consecutive clusters as mentioned above,we measure the spin correlations for every other site(cycles,inset of Fig.5(a)).To optimize the resolution,we embed 6 consecutive spins at the top of 3 horizontally consecutive clusters on a system of 12×12,and measure the spin correlations(squares,inset of Fig.5(a)).The spin correlations obtained by these two embedding types are similar(inset of Fig.5(a)).The spin correlations discussed above in the stripe phase are along its stripes.We also calculate the spin correlations vertical to the stripes at J2=0.7(green stars in Fig.5(b)).The curve is shifted by 10−0.3.The distant spin correlations along both directions are strong.In Ref.[35],the static spin structure factors,which are Fourier transformation of the spin correlations,have very sharp peaks in the stripe phase of the square lattice.These sharp peaks indicate strong distant spin correlations.This is consistent with our results.

3.2.Dimer correlation

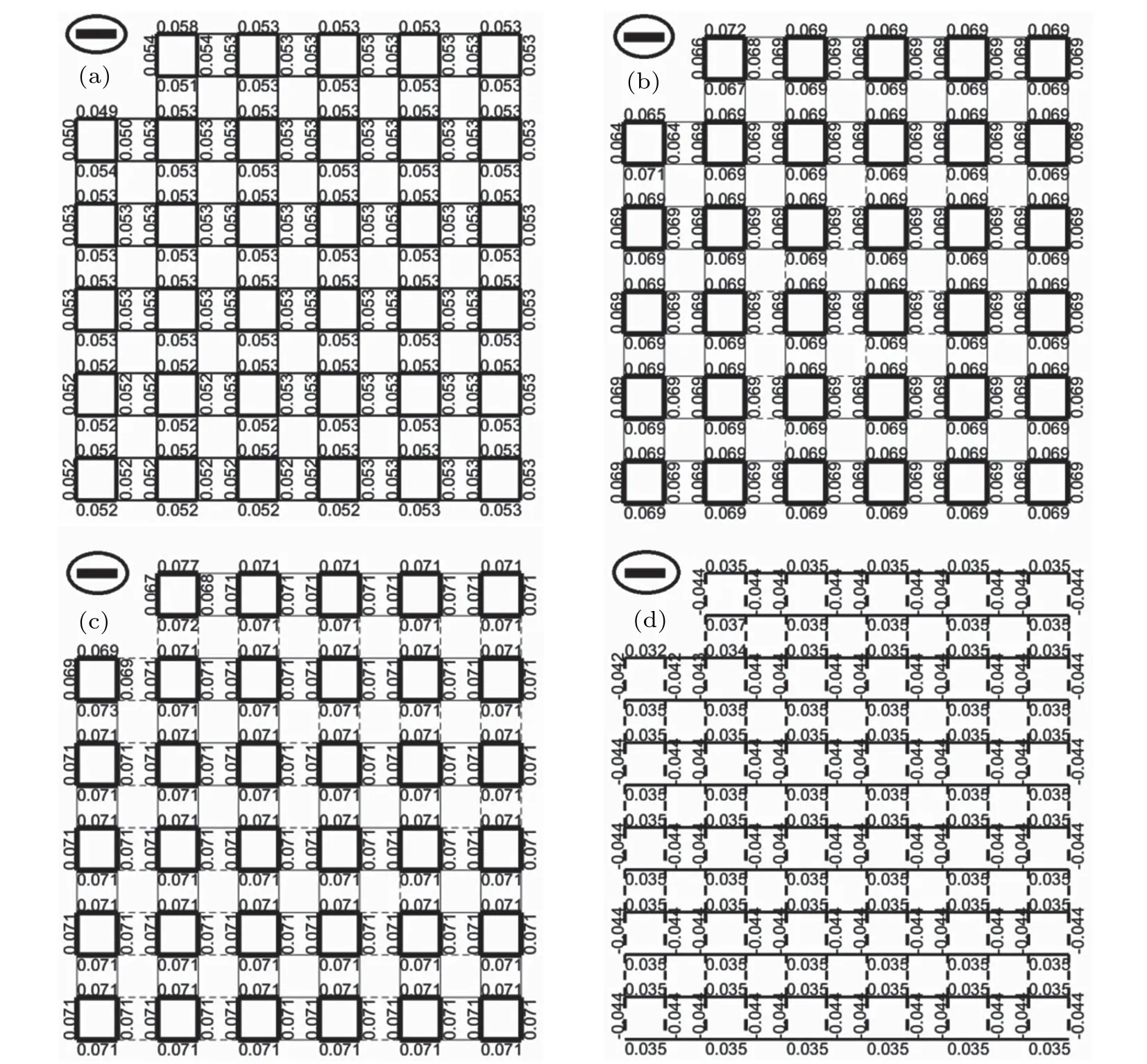
Fig.7.Dimer correlations on a 24×24 system for different J2 values:(a)(J2=0.2)in the Neel phase,(b)(J2=0.45)and(c)(J2=0.55)in the intermediate phase,(d)(J2=0.8)in the stripe phase.The reference dimer is denoted by the line in ellipse.Negative(positive)correlations are represented by dashed(solid)lines.One cluster is embedded.The reference dimer is in the embedded cluster.

4.Summary