含未知动态与扰动的非线性系统神经网络嵌入学习控制

2021-09-28闫一鸣徐东甫李志伟孙灵芳

自动化学报 2021年8期

马乐闫一鸣徐东甫李志伟 ,2 孙灵芳

非线性系统的高性能控制是控制科学与应用中的重要研究问题[1].非线性系统普遍存在于如电机力矩控制、康复系统人机交互控制等应用领域[2-3].由于非线性系统的复杂性,目前尚无如线性系统那样较为完善的分析与设计体系[4].非线性系统的稳定性分析、不确定性补偿、扰动抑制与性能优化是其中难点问题.特别是含有非线性动态与扰动因素的非线性系统控制性能优化问题亟待解决.

系统稳定性是非线性控制的首要问题.基于Lyapunov 控制(Lyapunov-based control,LBC)是非线性系统控制器分析与设计的重要方法[5].其优势在于稳定性分析证明能伴随控制器设计同时生成,Backstepping 方法是其中代表方法[6].文献[7]建立控制Lyapunov 函数(Control Lyapunov function,CLF),并利用Sontag 公式直接设计控制律,但通常寻找CLF 较为困难[8].虽然基于Lyapunov的分析与设计已被广泛采用,但其分析相对困难.同时对于上述方法当考虑不确定性与扰动等因素后,其稳定性分析的复杂度将陡增.

系统模型中的不确定性给分析与设计带来较大困难.对于模型形式已知但参数未知的不确定问题,参数自适应方法将参数误差视作时序量加入Lyapunov 函数,并建立参数自适应律,实现对参数不确定性的自适应.针对参数量繁多或者模型形式未知问题,文献[9]采用RBF (Radial basis function)神经网络作为系统模型中未知非线性项的逼近器,将未知非线性模型的逼近问题转化为对RBF 网络权值自适应逼近问题.文献[10]采用自适应神经网络方法解决了切换互联系统的非线性不确定问题,但未考虑控制增益的不确定性.文献[11]将逼近器进一步改进为一种双环递归神经网络,该模型考虑了逼近模型的内部时序状态,试图增强网络逼近能力.文献[12]采用模糊逻辑方法作为未知非线性的逼近器.虽然上述方法能有效逼近系统未知非线性项[13],但不确定性可能产生较大的初始逼近误差,影响系统动态性能.

扰动可视为控制过程中产生的独立于系统模型的不确定因素.虽然滑模与鲁棒等控制方法对一定范围内扰动具有抑制能力[14],但缺乏对扰动必要的量化与补偿机制[15].基于扰动观测器(Disturbanceobserver-based control,DOBC)控制方法则采用估计扰动并加以补偿的直接技术路线[16].其中文献[17]针对线性系统采用不确定扰动估计器(Uncertainty and disturbance estimator,UDE)同时估计不确定性与扰动并加以补偿.文献[18]在相关假设条件下,设计了针对死区非平滑问题的扰动观测器.扩张状态观测器(Extended state observer,ESO)提出了一种 “总扰动”思想,即模型未知动态、控制增益不确定性与扰动的整体作用视作等效扰动加以估计[19-20].

通过分析看出,围绕上述问题展开的工作根本目的是保持控制系统稳定.然而控制系统的暂态性能与稳态误差等因素也是控制品质的重要指标.文献[21]将反步控制与最优控制结合,针对模型确定且无扰动的高阶非线性系统逐步建立可学习的最优控制器.文献[22]结合辨识方法提出了自适应迭代学习控制(Iterative learning control,ILC)方法,实现了位值时变线性系统控制.然而ILC 需要重复任务条件并且对扰动较为敏感[23].文献[24] 采用Hammerstein 神经网络作为辨识模型,建立跟踪误差目标函数在线调节PID (Proportion integral differential)神经网络控制器,然而辨识初始值和扰动等因素导致的辨识误差会影响性能,甚至导致系统不稳定.

以上分析得出,非线性系统中的动态不确定性与扰动问题对于控制性能影响较大,目前研究仅集中在对上述因素的补偿与抑制方面,对于带有不确定性与扰动的控制问题缺乏有效的性能优化手段.另一方面,近年来深度学习技术成绩斐然[25],利用深度学习提升控制性能将是积极有效的途径.文献[26]采用卷积神经网络(Convolutional neural network,CNN)作为辨识器结合自适应控制实现了直升机控制,在基于深度学习的性能优化方面做出了尝试.文献[27]则采用卷积神经网络作为系统不确定项的逼近器并结合滑模控制实现自适应控制.基于确定性策略梯度的深度强化学习(Deep deterministic policy gradient,DDPG)对于深度Q 神经网络(Deep Q network,DQN)作出改进,使其能适用于状态与控制输出均为连续值的控制问题[28].文献[29]对两种深度强化学习控制的优化能力作出了量化比较.然而大部分深度强化学习控制方法缺乏必要的稳定性分析,在实际应用中存在隐患,这也是该技术未能广泛用于实际控制的原因之一[30].

从上述分析看出,现有研究未能将深度学习充分应用于控制问题中,主要原因如下:1)上述研究中深度神经网络的作用是作为未知动态的逼近器或辨识器,仅将问题转为确定性系统控制,因此控制性能的上限仅为基础控制器对于该确定性系统的性能;2) 作为逼近器的深度神经网络被简化成了如RBF 函数的线性基函数形式[31],其内部结构与参数未能对系统性能优化作出贡献;3)多数深度强化学习控制缺乏必要的稳定性分析,难以保证实际应用稳定.因此在稳定条件下,如何充分灵活地利用深度神经网络的结构与优化优势提升非线性系统控制性能是值得深入研究的问题.

综上,本文写作动机可描述为:针对具有未知动态与扰动的非线性系统,在少量假设条件下建立既确保Lyapunov 稳定,又简洁灵活的学习控制器,同时该控制器能在无需辨识条件下利用深度学习技术进行在线优化以实现性能提升.为此本文提出一种Lyapunov 稳定的神经网络嵌入学习控制方法.

本文主要工作内容如下:

1)提出了基于神经网络嵌入学习控制器设计方法,在已知Lyapunov 稳定控制器中嵌入神经网络控制器构成可优化的学习控制器,并通过定理1证明新的控制器仍保证Lyapunov 稳定.(详见第1 节)

2)利用导数等价条件,建立改进的性能优化目标函数,以用于学习控制器优化.改进后的目标函数可规避辨识环节,直接利用输出反馈优化控制器.(详见第2 节)

3)受文献[19]启发,基于Lyapunov 方法直接建立未知非线性动态、时变扰动与控制增益不确定的等效值自适应方法.(详见第3 节)

本文主要创新贡献如下:

1)不同于现有方法,本文神经网络并非用于逼近系统非线性函数,而是作为用于性能优化的控制分量.在满足Lyapunov 稳定条件下,神经网络结构可任意构造与调整,且无需额外的理论分析过程,从而解放了神经网络控制对模型形式的束缚.由于神经网络形式任意,因此大量的深度神经网络模型可简单直接地嵌入控制器中,并仍保持Lyapunov稳定,所以本文方法粘合了深度神经网络技术和控制理论与应用的研究缝隙.

2)改进的性能优化目标函数规避了辨识过程,从而避免了辨识误差对控制的影响.同时因上述的稳定性保证,可在线实现目标函数优化.

3) 建立的值自适应方法相比传统方法,无需RBF 网络等模型作为逼近器,同时具有更快的估计速度与精度.

1 神经网络Lyapunov 稳定嵌入

设一类带有模型不确定性与扰动的n阶m维状态反馈系统为S:x×u →x,其中x∈Rn×m为系统状态向量,u∈Rm为系统控制输入向量,第i(i=1,2,···,n－1) 阶系统为=xi+1,第n阶为:

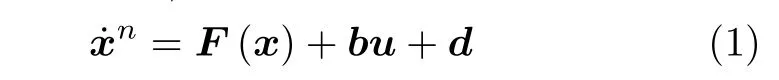
式中,F∈Rm为未知非线性函数向量,d∈Rm为有界未知扰动向量,b＞0 为m阶未知可逆对角常数矩阵.

定理 1.设Lyapunov 函数V导数满足:

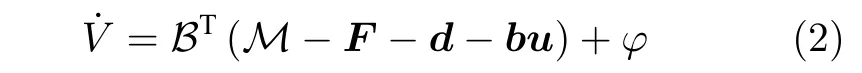
其中,B与M为以状态x为变量的m维已知函数向量,φ为不含u的其余项之和.若满足:1)存在基础控制器ub使系统Lyapunov 稳定,即＜0;2)存在向量函数ϑ满足Biϑ(Bi)≥0;3) 存在神经网络μ(·|θ)≥0,其中θ为神经网络全部可调参数构成的列向量,则式(3)神经网络嵌入控制器对系统SLyapunov 稳定.

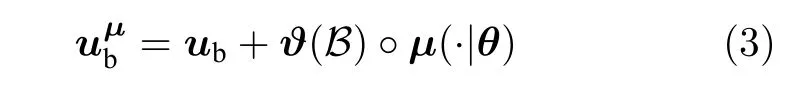
其中,°为Hadamard 积运算符.

证明.将式(3)代入式(2)得:

注 1.由式(3)看出,本文学习控制器是基于已有Lyapunov 稳定的控制器建立,因此在应用中本文方法的稳定性分析难度较低.并且控制器对神经网络的形式无具体要求,仅需满足网络输出非负.确保该条件相对容易,仅需将网络输出层激活函数设置为非负函数即可.

定理 2.对于系统S,设有给定基础控制器ub与神经网络控制器μ(·|θ),根据式(3)构成学习控制器的函数空间为,则对于任意表征系统控制性能的量度L(S,u) (小值更优),均满足:

注 2.本文主旨并非求解最优控制器,而是通过式(3)建立满足式(5)的学习控制器.

2 神经网络学习控制器性能优化

第1 节论述方法将深度学习及优化技术稳定地引入到非线性控制中.得益于深度学习中自动求导技术与优化方法,使研究者摆脱了繁杂参数推导,研究者可针对问题本身专注于网络结构与优化问题的设计中.因此神经网络学习控制器性能优化可归结为对控制性能目标函数的设计问题.为此建立能表征系统控制性能的目标函数.跟踪误差是控制问题的首要指标,因此需讨论以其为优化项的目标函数:

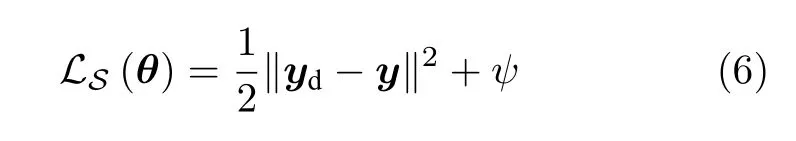
其中,yd为系统当前期望,y为系统当前实际输出,ψ为表征其他控制指标正则项,且对控制器梯度已知.

目前主流的神经网络优化方法为基于梯度的方法,式(6)LS对θ的梯度为:

因此将式(6)修改为:

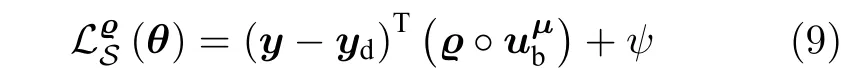
其中,ϱ＞0 为可调小范数常值参数向量.根据式(8)得出,关于θ的梯度仅相差常数向量ς,即:

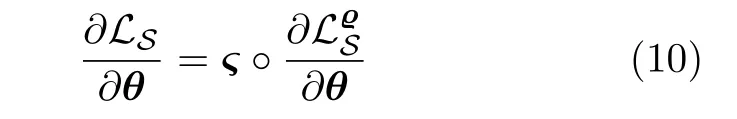
基于梯度的优化方法在更新迭代时通常对梯度乘以某小值正数,即学习律.因此可通过调节学习律来消除式(10)所述差异带来的影响.特别是对单输入–单输出系统,式(10)中的梯度差异问题可完全折算到学习律的调节.综上得出,对于梯度优化方法,式(6)问题可等价为求解式(9)问题.

式(9)相对于式(6)优势在于不需对输入输出进行建模或辨识,直接利用观测输出y,避免了估计误差.同时由于改进后的优化问题仅需输出反馈并可单值优化,因此控制器支持在线学习.

注 3.根据文献[32]结论,对于单值优化问题,学习律非敏感参数,因此在应用中若适当选定学习率,即便对于多输入多输出问题,式(10)影响也可忽略.

3 未知非线性与扰动等效值自适应

前两节分析了Lyapunov 稳定条件下神经网络嵌入与性能优化方法,可将任意结构神经网络嵌入基础控制器中并利用其优化控制性能.但本文方法的应用前提是存在使系统稳定的基础控制器.由于式(1)描述系统中存在未知非线性项与未知控制增益等不确定性与扰动问题,因此基础控制器设计中需对上述问题加以处理以确保基础控制器满足稳定条件.

为此本节建立一种未知非线性与扰动的等效值自适应方法.该方法的特点是无需逼近器模型,仅用值更新即可实现对未知时变不确定项的自适应.

注 4.本节目的是建立对不确定性与扰动具有补偿与抑制能力的基础控制器,上述方法并不依赖于本节内容.即任何保证式(1)描述系统的其他控制器都可以结合上述方法构成神经网络学习控制器.

首先将式(1)变换为:

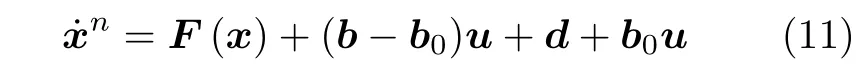
其中,b0为m阶已知对角常值矩阵.并定义:

注 5.注意到自适应律中采用了信号微分项,虽然文献[33-34]中证明了该方法的合理性,但考虑实际信号中的噪声问题,本文采用适当微分器加以处理.关于微分器的收敛性可参见文献[35].

综上,本文提出的针对未知非线性动态与扰动系统的神经网络嵌入学习控制器表示如下:

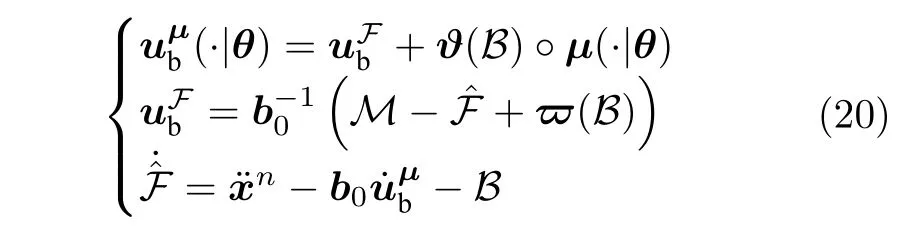
4 仿真分析

本节以带有三角函数、死区与摩擦特性的一、二阶非线性数值模型与实际物理模型进行仿真测试.全部仿真基于Python 框架,采用Pytorch 作为深度神经网络库.本节与经典RBF 自适应控制和文献[13]中自适应方法作对比,以测试本文方法性能.仿真测试中神经网络结构与相关参数设置见附录.

4.1 数值模型算例

算例1.考虑一阶非线性系统:

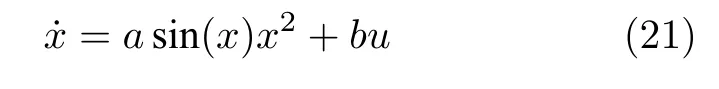
其中,a=3.0,b=1.0.设计基础控制器:

其中,yd为控制期望.

基于ub分别设计经典RBF 自适应、值自适应、神经网络学习三种控制器(在值自适应基础上嵌入神经网络控制器),并比较仿真结果.其中统一取k=36,b0=2.0,RBF 核函数σ=1,在[-6,6]范围内等分取100 个核函数中心值,值自适应与神经网络学习控制采用自适应方法估计fˆ 值,经典RBF自适应方法则采用径向基函数估计.

图1 为期望轨迹yd=sin(t) 三种控制方法的仿真对比结果,以平均绝对误差(Mean absolute error,MAE)为评价指标.图1 结果显示:1)虽然经典RBF 方法的输出响应与控制输入随时间增加逐渐趋于本文方法,但本文的值自适应与神经网络学习方法的跟踪效果明显优于经典RBF 方法.原因在于未知非线性函数导致RBF 初始估计与实际差别较大,同时RBF 估计收敛速度低于值自适应方法,因此得出对于上述系统本文方法优于经典RBF 方法.2) 值自适应与神经网络学习控制方法的输出基本一致,但后者的跟踪误差低于前者,因此得出对于上述系统神经网络学习控制方法能根据跟踪误差目标函数调节神经网络,实现控制性能优化.

图1 算例1 控制性能结果Fig.1 The controllers performances of the Example 1

算例2.再考虑带有三角函数与死区的二阶非线性系统:

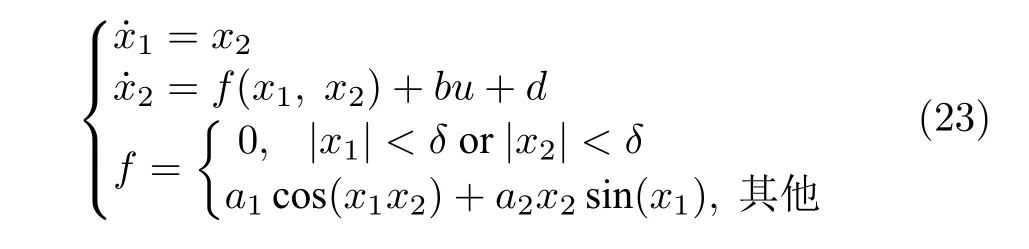
其中,δ=0.1,a1=3.0,a2=6.0,b=3.0.

根据式(20)设计基础控制器:

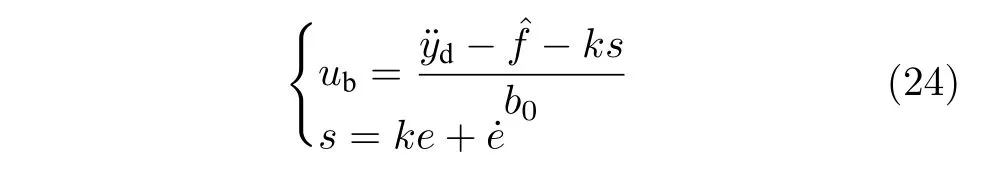
其中,e=yd－y.本算例中统一取k=10,b0=5,RBF核函数σ=1,在[-12,12]范围内分别对x1与x2进行10 等分取值,即取100 个c值,其他参数同上例.

图2 为yd=sin(t),d=0 三种控制方法的仿真对比结果.图2 结果显示:1)三种方法均能以较高精度实现式(23)系统的轨迹跟踪,由图2 (a)看出不同于前一算例,RBF 方法在波峰处输出值高于期望,在波谷处低于期望,而其他两种方法则与其相反,原因在于RBF 对的估计方式与本文提出方法不同,加之与前一算例的模型差异导致图2 (a)效果;2)图2 (b)中的控制输入u的峰值与频率均高于前一算例且出现震荡,原因在于本算例系统阶数增高且多出死区非线性,进而导致上述现象;3)三种方法的控制输出幅值大体一致,跟踪误差排序仍为经典RBF ＞值自适应＞神经网络学习控制.综上得出,对于带有三角函数与死区的二阶非线性系统,本文方法效果优于经典RBF 自适应方法,且神经网络学习控制方法能在不明显提升控制输出条件下优化基准控制器性能.

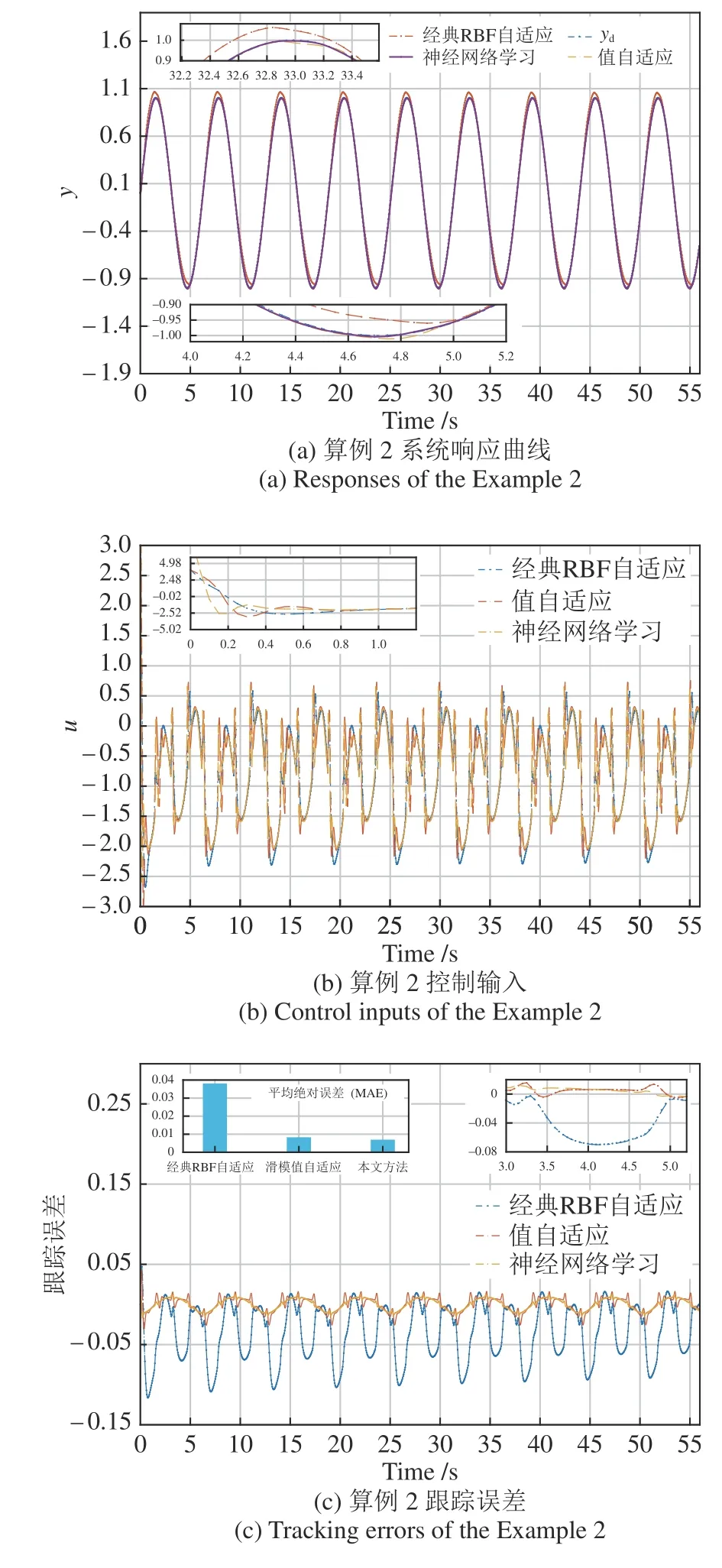
图2 算例2 控制性能结果Fig.2 The controllers performances of the Example 2

算例3.上述模型加入如下扰动:

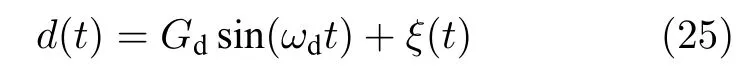
其中,Gd=100.0,ωd=10.0,ξ(t) 为[-30,30] 随机量(三种方法ξ(t) 相同).沿用前算例控制器进行仿真测试以比较三种方法在扰动条件下的性能,其中控制参数取k=35,b0=1.0.

图3 为yd=sin(t)+sin(0.5t) 三种控制方法的仿真对比结果.图3 结果显示:1)在强扰动条件下三种方法均实现对yd的稳定跟踪,但三种控制输出均出现随机震荡,如图3 (a),其原因在于施加的扰动中含有较大随机扰动;2)图3 (b)中的控制输入u幅值范围与频率均高于前一算例且震荡,原因在于yd高于前一算例且加入了高频扰动,同时为了抑制强扰动,控制增益高于前例;3)三种方法控制输出幅值大体一致,跟踪误差排序仍为经典RBF ＞值自适应＞神经网络学习控制.由此表明,在强扰动条件下本文方法对不确定性与扰动的补偿和抑制能力优于经典RBF 自适应方法,同时本文提出的嵌入神经网络控制器仍能优化基准控制器性能.

图3 算例3 控制性能结果Fig.3 The controllers performances of the Example 3

4.2 物理模型仿真

本节采用与第4.1 节不同结构的神经网络作为嵌入控制器(详见附录描述),对实际物理模型测试,并与文献[13]方法(一种基于Backstepping 方法的神经网络自适应控制方法,下称 “对比方法”)作对比以验证本文方法的先进性.

算例4.指数摩擦特性的电机转矩控制模型如下:

其中,θ为电机转角(单位rad),ω为其角速度(单位rad/s),τ为控制输入(单位 N ·m),fM为其非线性项,Tf为摩擦力.模型参数为:K=2.97,Kθ=0.25,T=0.632,Tc=0.2 N·m,Ts=0.3 N·m,α=1.0. 施加如式(25) 扰动,Gd=10.0,ωd=1.0,ξ为[-10,10]随机数.

沿用前节方法构造本文方法的基础控制器,b0=1.0,k=50.0 (根据对比方法设置的参数k值),神经网络结构与参数见附录.对于算例4,文献[13]方法性能趋于最佳的参数设置如下:在[-10,10]范围内分别对x1,x2进行36 等分取值,即取1 296 个值作为对比方法中的RBF 神经网络节点中心值,设置对比方法的α1,α2分别为30.0 与50.0,其余参数见文献[13].

图4 为yd=π sin(t) (rad)两种方法的控制效果对比.从中看出:1)图4 (a)显示两种方法均能快速稳定实现轨迹跟踪,然而对比方法在初始阶段较本文方法有较大误差(见第一次波峰波谷);2)图4 (b)显示两种方法的控制输入基本一致,本文方法较对比方法无明显提升;3)图4 (c)显示本文方法的跟踪误差总体上低于对比方法.因此可得出本文方法对于算例4 的控制效果整体优于对比方法.

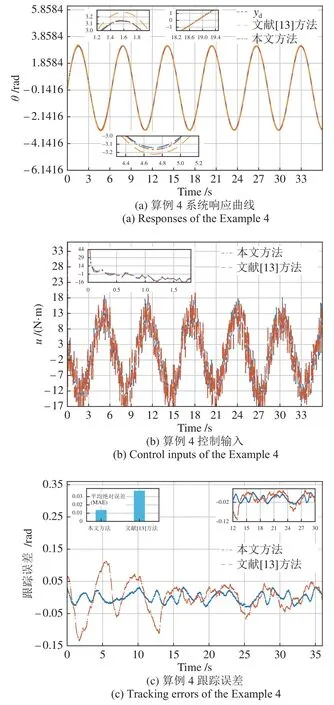
图4 算例4 对比实验控制性能结果Fig.4 The results for comparison test of control performances of the Example 4

对比两种方法的最大误差(m ax|e|)、平均误差(m ean|e|)、最大控制输出(m ax|u|)、平均控制输出(m ean|u|)、最大不确定与扰动估计误差(m ax)与平均不确定与扰动估计误差(m ean) 6 种量化指标,如表1.从表1 看出本文方法 m ax|e|低于对比方法 4 1.63%,m ean|e|低于对比方法 41.66%,max|u|低于对比方法 2.63%,m ax低于对比方法 1 1.32%,mean低于对比方法 1 1.14%,仅 m ean|u|略高于对比方法 2.58%.

表1 算例4 两种方法控制性能统计数据对比Table 1 The comparison for control statistical indicators of two methods in the Example 4

以上分析得出本文方法的控制性能整体优于对比方法,原因如下:1)对比方法RBF 网络仅为对不确定项的逼近,控制性能上限取决于Backstepping 控制器,同时初始时刻的未知动态与网络估计值有较大差距,因此导致对比方法在第一次波峰、波谷阶段的误差较大;2)本文方法的值自适应方法能够较为快速地估计不确定性与扰动,因此在初始时刻误差低于对比方法;3)本文方法的神经网络控制器中设计了前馈结构对控制性能有积极贡献,本文优化方法能够有效地调节网络参数与输出从而优化控制性能.

综合以上算例得出,本文提出的值自适应方法相比经典RBF 方法对三角函数、死区与摩擦非线性和强扰动未知不确定系统具有更好的模型估计与扰动抑制能力,嵌入神经网络控制器能在不提升控制输出幅值条件下优化基准控制器性能.性能优化结果充分证实了第2 节中提出的梯度等效优化方法的合理性与有效性.与对比方法的对比实验结果表明,本文方法在对不确定与扰动的补偿与抑制和控制性能优化方面具有一定的先进性.算例中采用不同结构的神经网络构建学习控制器,体现出基于本文方法引入的深度学习及优化技术可针对具体控制问题灵活地设计与调整网络结构.

5 虚拟实验分析

前节已对本文方法控制性能作出较充分的比较分析,因此本节专注验证本文方法解决实际问题的有效性.上肢康复机器人控制问题中涉及不确定性、扰动与性能优化等方面,因此选择该问题为应用实例,针对神经网络的在线调节与训练后运行两种方式的控制效果进行对比分析.本文基于CoppeliaSim 物理模拟系统搭建虚拟实验平台,如图5 所示,本文中仿真控制周期为0.01 s,物理引擎选择Bullet 2.87,精度设置为 “最高精度”.以下虚拟实验基于Python 3.7 的控制周期均小于10 ms,即所有实验的控制频率可达到100 Hz 以上.

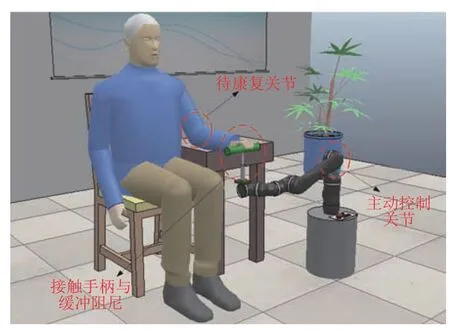
图5 CoppeliaSim 虚拟实验示意图Fig.5 The demonstration of virtual experiment in CoppeliaSim

采用系统提供的Python 远程同步API (Application programming interface)方式实现控制.对于控制端物理虚拟系统模型及参数未知,因此机械臂关节控制模型表示为:

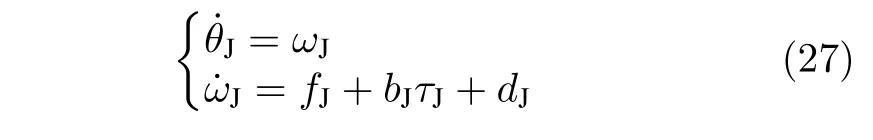
其中,θJ为康复机器人主动关节角度(单位rad);ωJ为其角速度(单位rad/s);fJ为控制系统未知非线性动态项;bJ为关节未知转动惯量(单位 k g·m2);τJ,dJ为关节控制力矩与未知扰动项.选定同前节的基础控制器,分情况测试分析实际系统控制效果.

5.1 不同体重康复者测试

由于用户个体差异,上肢体积与重量不尽相同,以至施加于系统的负载不同.分别选取偏瘦、中等、偏胖三种身形用户,测试在不同负载条件下的控制性能.设主动轴角度期望轨迹为=0.3 sin(t)+y0,y0=2.7,训练方式经5 min 运行完成神经网络训练,两种方式测试时间为1 min.

本节基础控制器沿用式(22),其中k=30.0,bJ=16.0 kg·m2,网络结构与参数见附录.图6 为不同身形用户两种方式的跟踪误差MAE与控制输入幅值MAE的统计图.从中可得出:1) 两种方式对于不同身形用户测试中均有有更低的控制误差;2)两种方式的控制输入幅值基本相等,表明训练过程没有明显提升控制输入幅值.

图6 不同体重康复者测试跟踪误差与控制输入MAEFig.6 The MAE of tracking errors and control inputs for tests to rehabilitation clients with different weights

5.2 不同康复任务性能测试

不同康复人群需制定不同的方案以达到康复目的,为此选择两种关节康复轨迹测试不同康复任务的系统控制性能.设任务1 的康复轨迹为0.2 sin(t)+y0,y0=2.7;设任务2 的康复轨迹为δ=3.0.

图7 为不同任务轨迹的两种方式跟踪误差MAE与控制输入幅值MAE 统计图.对于两种任务轨迹,从图中可得与前例类似结论.此外两种方式对于任务2 的误差高于任务1,原因之一在于任务2 在任务1 基础上增加了饱和条件,因此饱和段跟踪误差会有所提高,可加大训练时长提升控制精度.

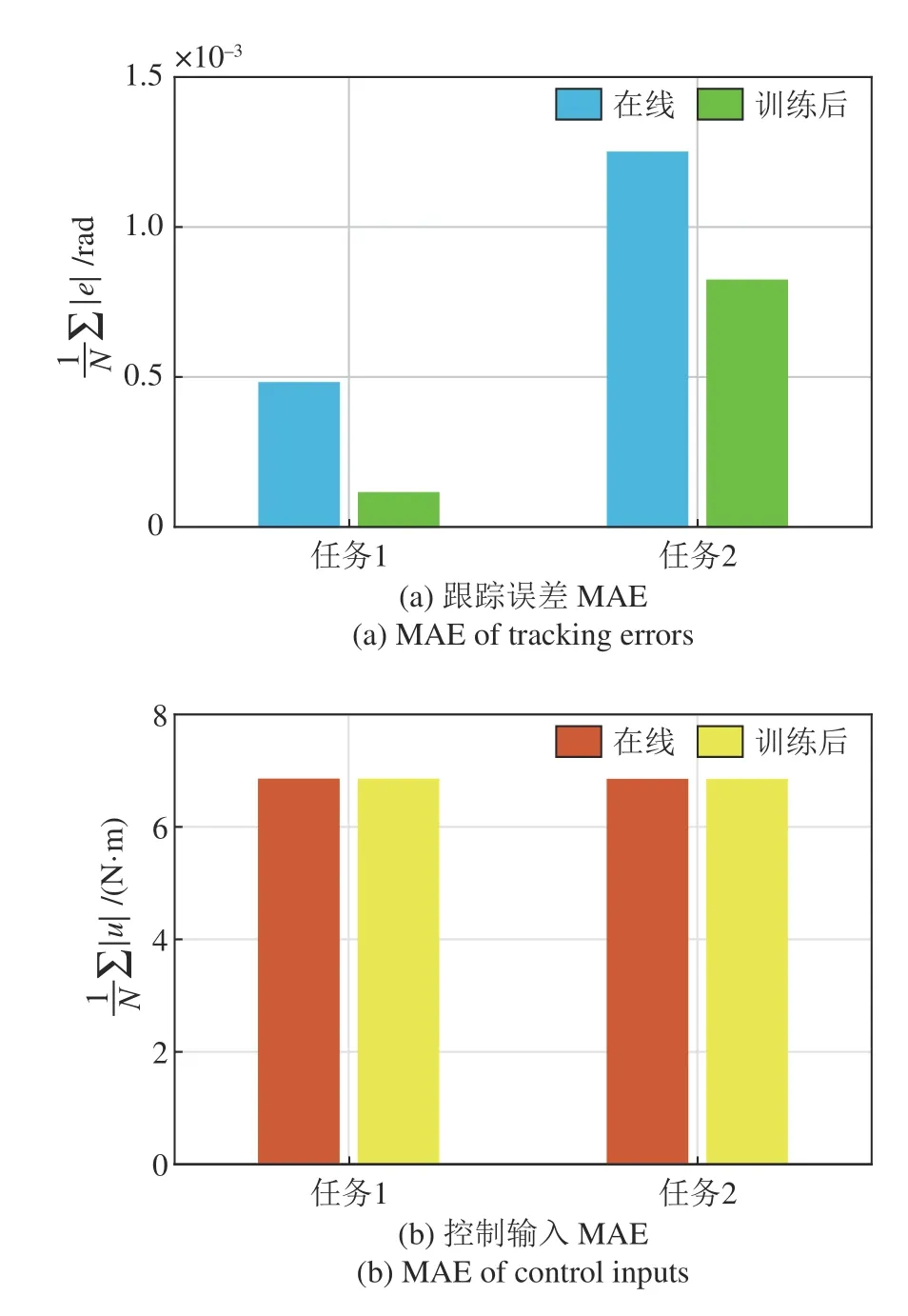
图7 不同康复任务测试跟踪误差与控制输入MAEFig.7 The MAE of tracking errors and control inputs for tests to different rehabilitation tasks

5.3 用户异步扰动测试

康复训练过程中,用户可能自发运动上肢关节,该运动可视为康复机器人系统扰动,或导致与系统出现异步相位差.本例在虚拟康复运动中施加用户关节动态力矩,该力矩通过手柄传导作用于机器人主动关节.设用户上肢关节力矩为τd=0.1 sin(t) (N·m),期望轨迹为=0.2 sin(t)(rad).

本节采用文献[27] 中的基于卷积神经网络(CNN) 控制和文献[28] 中的深度强化学习控制(Deep reinforcement learning,DRL)方法作为对比方法,测试用户异步扰动问题的控制性能.

为使对比结果更具说服力,本测试中三种方法所需的神经网络被设置成相同的结构与参数.均采用如文献[27] 中描述的两层卷积神经网络.输入统一设置成由状态向量时序组成的矩阵,第i行状态向量为:τ(t－ζi+1)],其中ζi=Δt(i－1)(s),Δt=0.01 s,i=1,2,3,···,N为延迟时间常数.本文N=6,因此本文卷积网络的输入维数为 6×5 矩阵,CNN 两层卷积核数均为10,卷积核大小为 3×3. 此外本文方法其他参数同前节.

文献[30]中DRL 方法的单次学习批数NBatch=50,奖励函数γ设计如式(28),CNN 与DRL 方法其他相关参数设置见文献[27-28].

其中,e=J.

图8 为带有康复者关节扰动的机器人控制对比实验结果.需说明:1)因各方法的最大与平均控制转矩输出的绝对值基本相等,因此未出图展示;2)图中显示的DRL 控制曲线是经多次学习并收敛后(meanγ ＞0.99)的效果.从图8 (a)看出所有方法均能快速稳定地实现期望轨迹跟踪,但从第一次波峰与波谷处曲线看出,CNN 与DRL 方法相对本文方法具有较大误差,虽然本文方法在第一次波峰处有震荡,但跟踪误差均小于对比方法.从末次波峰、波谷处曲线看出,DRL 方法的跟踪误差仍明显高于其他方法,虽然CNN 方法比第一次波峰降低了误差,但相对本文方法仍有一定差距.从图8 (b)看出,由于初始时刻的系统不确定性与扰动作用,所有方法均出现不同程度的抖动,但本文方法整体误差最小,CNN 居中,DRL 方法则出现了较大的单向误差(误差值全为正).图8 (b)中的MAE 指标(单位rad)分别为:本文方法在线效果 9.645×10-4,本文方法训练后效果 8.476×10-4,CNN 方法 4.003×10-3,DRL 方法 9.515×10-3,因此可看出本文方法控制精度明显优于对比方法,且经训练后的控制精度高于在线精度.

图8 带有康复者关节扰动的机器人控制对比实验结果Fig.8 Comparison results of robot control methods for joint disturbances created by rehabilitation client

上述对比实验结果分析如下:1) DRL 方法的控制精度最低源于方法本身固有的优化瓶颈问题,当达到一定精度后因平均奖励函数趋于上限(meanγ ＞0.99),导致精度提升逐渐缓慢,同时因缺乏稳定性保障,DRL 方法探索学习具有一定的随机性,在实际应用中难免发生失控问题,该随机性或造成了单向误差现象;2)虽然CNN 相对RBF 具有模型优势,但文献[28]中的CNN 方法仅用其逼近不确定项,未充分发挥CNN 模型上的优势,因此CNN 方法性能上限仅为基础控制器对确定性系统的控制性;3)本文方法具有稳定性保障和性能优化手段,因此能在使用相同结构与参数的CNN 网络构造控制器条件下,呈现较高精度效果.综上,由对比实验结果与分析得出,本文方法相较其他深度学习控制方法具有一定的先进性.

由本节三类虚拟实验结果得出,对上肢康复机器人控制系统问题,本文方法在系统非线性动态完全未知条件下对于用户体重、任务类型与关节扰动等不确定非线性问题具有良好的控制性能,从而验证了本文方法应用于实际问题的有效性.经过训练后的控制效果均优于在线更新,进一步证实了本文提出的梯度等效优化方法的有效性.因此可推测,实际应用中本文方法可通过神经网络学习不断优化各实际工况的控制品质.同时与其他相关深度学习控制方法的对比实验,证实了本文提出的神经网络嵌入与优化方法对于实际系统控制具有一定的先进性.

6 结束语

通过分析与测试结果得出如下结论:1)本文方法通过神经网络控制器的嵌入在满足Lyapunov 稳定条件下有效地优化了基准控制器性能;2)改进的优化目标函数能够有效地优化跟踪误差性能,规避了辨识环节并支持在线学习;3)本文方法对函数时变与随机扰动具有较强的抑制能力,对非线性系统的未知动态项具有良好的估计能力.综上,本文提出方法相对传统方法在性能优化、不确定性与扰动的补偿与抑制方面具有实用性和一定的先进性.

未来将从如下方面开展工作:1)将方法适用范围扩展至输出反馈系统;2)引入其他控制性能指标并设计相应的优化函数;3) 扩展应用领域至多输入–多输出系统.

附录A.神经网络结构说明

本部分主要描述仿真与实验部分设计的神经网络结构、函数、参数等相关细节.

首先对于式(3)中涉及的ϑ函数,本文采用改进的sigmoid 函数:

其中,α≥1 为增益系数,λ＞0 为缩放系数.选择该函数理由为其导数相对平坦,且增益与有效区域可调.

仿真与实验中采用了不同结构的神经网络以说明本文方法对于神经网络结构的广泛适用性.

图A1 为仿真测试中算例1～3 和5.1 节、5.2 节中采用的神经网络结构.该结构属于一种前向多层感知器,其中X为网络输入向量;μ为网络输出向量,其具体含义为嵌入学习控制器的输出量;W与G分别为网络可调权值矩阵(以W与G全部参数构成的向量即式(3)中的θ);H与Y为网络中间向量.Γ为激活函数,本文采用LeakyReLU 函数:Γ(x)=max(βx,x),β=0.18.

图A1 算例1～3 与5.1 节、5.2 节学习控制器神经网络结构Fig.A1 The architecture of neural network of learning controller in exmples 1～3 and subsection 5.1～5.2

从输入X到嵌入控制器输出μ关系式如下:

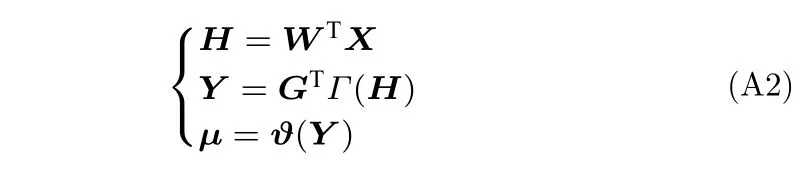
算例1～3 网络输入X为 [x1,x2,yd,,u(t-ζ)]T,其中x1,x2,yd,,u分别为算例1～3 中的状态变量、期望输出及其导数和控制输出,ζ(ζ=0.01 s)为延迟参数.5.1 节和5.2 节中,网络输入分别为机械臂关节角度、角速度、关节期望角度及其导数和关节控制转矩.

因此W,G维度分别为hi×5,hi×1,hi表示第4节中算例i所对应的向量H的维度,分别为 18,36,30.5.1节和5.2 节向量H的维度分别为 36 与30,采用Adamax作为优化方法.

图A2 为算例4 中本文方法采用的嵌入神经网络,该网络属于一种变形的MLP (Multi-layer perceptron)结构.考虑了控制中的前馈机制,该网络在图A1 的网络内加入了一条前馈支路构成了分层MLP 网络.其中Xf与Xb为网络输入向量,μ为网络输出,含义同上.Wf,Wb,Gf与Gb为网络权值矩阵,上述4 个矩阵全部元素构成的向量即为网络的参数向量θ.Hf,Hb,Yf,Yb和Y为网络中间向量.Γ函数同上一模型.