基于深度强化学习的双足机器人斜坡步态控制方法

吴晓光 刘绍维 杨 磊 邓文强 贾哲恒

服务机器人融合了机械、控制、计算机、人工智能等众多学科,在各个领域得到应用,如足式机器人[1]、水下机器人[2-4]、无人船舶[5]、无人飞行器[6]等,是目前全球范围内前沿高科技技术研究最活跃的领域之一.双足机器人是服务机器人中的一种仿人足式移动机器人,能够适应街道、楼梯、废墟等复杂的地形环境,可替代人类从事救援、医疗、勘探、服务等行业.在双足机器人中,基于被动步行(Passive dynamic waking)[7]理论设计的被动双足机器人,因结构简单、步态柔顺、能耗低等优点受到广泛研究.被动双足机器人可充分利用自身动力学特性,仅依靠重力与自身惯性便能沿斜坡向下行走.然而,被动双足机器人在行走过程中因缺乏主动控制,存在步行稳定性差、抗扰动能力弱等不足.为弥补这些不足,研究人员通过对被动双足机器人部分关节施加控制,研发出准被动双足机器人[8],提升了双足机器人的步态控制能力.

为进一步提高准被动双足机器人步行稳定性,步态控制方法的研究逐步成为准被动双足机器人研究领域的重点方向,现有的控制方法包括神经网络[9]、延时反馈控制[10-11]、能量成型控制[12-13]、强化学习[14]等.其中,强化学习(Reinforcement learning,RL)因易于实现、适应性好、无需先验知识等优点而得到广泛应用.Tedrake 等[15]利用随机策略梯度(Stochastic policy gradient,SPG)算法实现无膝双足机器人Toddler 的步态控制,使其能够在不平整路面上行走.Hitomi 等[16]则将SPG 应用于一种圆足有膝双足机器人的控制中,实现机器人在[0.02,0.04] rad 斜坡范围上的稳定行走,并提升了机器人对外界扰动的鲁棒性.Ueno 等[17]采用改进的行动者-评论家(Actor-critic,AC)算法提高了具有上肢双足机器人的步行稳定性,使机器人在20 组实验中完成19 次稳定行走.然而,上述算法均受RL 的结构、学习能力的制约,存在样本利用率低、学习不稳定、算法不易收敛等缺陷,严重限制了RL 对机器人步态的控制能力.

近年来,结合强化学习和深度学习的深度强化学习(Deep reinforcement learning,DRL)快速发展,迅速成为人工智能领域的研究热点[18].DRL 利用深度学习的优点克服传统RL 中的缺陷,广泛应用于自动驾驶[19-20]、自然语言处理[21-23]等领域,并被引入到双足机器人的步态控制研究中.在主动双足机器人中,赵玉婷等[24]利用深度Q 网络(Deep Q network,DQN)[25]算法,有效抑制了机器人在非平整地面行走时姿态角度的波动.在准被动双足机器人中,Kumar 等[26]将有膝双足机器人视为智能体,利用深度确定性策略梯度(Deep deterministic policy gradient,DDPG)[27]算法,实现机器人长距离的行走.此外,DRL 研究中也常将双足机器人作为控制对象,如MuJoCo[28-29]中的2Dwarker 模型、Roboschool[30]中的Atlas 模型等.

由于准被动双足机器人步态稳定的判别较为困难,DRL 在控制准被动双足机器人时,通常以行走的更远为目的,忽略了机器人步行稳定性、柔顺性等因素,这导致DRL 控制下机器人步态与稳定步态之间存在较大的差异.针对此问题,结合传统RL 在准被动双足机器人步态控制方面的不足,本文提出了一种基于DRL 的准被动双足机器人步态控制方法,实现较大斜坡范围([0.04,0.15] rad)下的机器人不稳定步态控制,使机器人能够抑制跌倒并快速恢复至稳定步态,达到提高机器人步行稳定性的目的:1) 建立准被动双足机器人动力学模型,确立机器人的状态空间与动作空间.2) 针对DDPG的不足,基于优先经验回放(Prioritized experience replay,PER)[31]机制,引入分布式优先经验回放(Distributed prioritized experience replay,DPER)[32]结构,建立高效的机器人步态控制方法 — Ape-X DPG 算法.3) 基于准被动双足机器人的行走特性设计的Episode 过程,结合机器人步态变化与缩放动作构建的奖励函数,为Ape-X DPG 的高效学习提供支撑.4) 通过仿真实验,对Ape-X DPG 的学习能力和步态控制能力进行测试分析,验证步态控制方法的有效性.

1 双足机器人动力学模型

1.1 动力学模型建立

本文以直腿前向圆弧足机器人作为研究对象,构建其动力学模型,机器人物理模型如图1 所示.机器人由连接在髋关节H处的两条完全一致的刚性直腿组成,被动步行时具有两个自由度,分别位于支撑点s与髋关节H处,记为θ1与θ2.为实施主动控制,在机器人髋关节与两腿的踝关节处设有电机.对机器人行走过程做运动简化[33],可将行走过程划分为摆动阶段和碰撞阶段,机器人被动步行过程如图2 所示.

图1 机器人模型示意图Fig.1 Sketch of the biped model

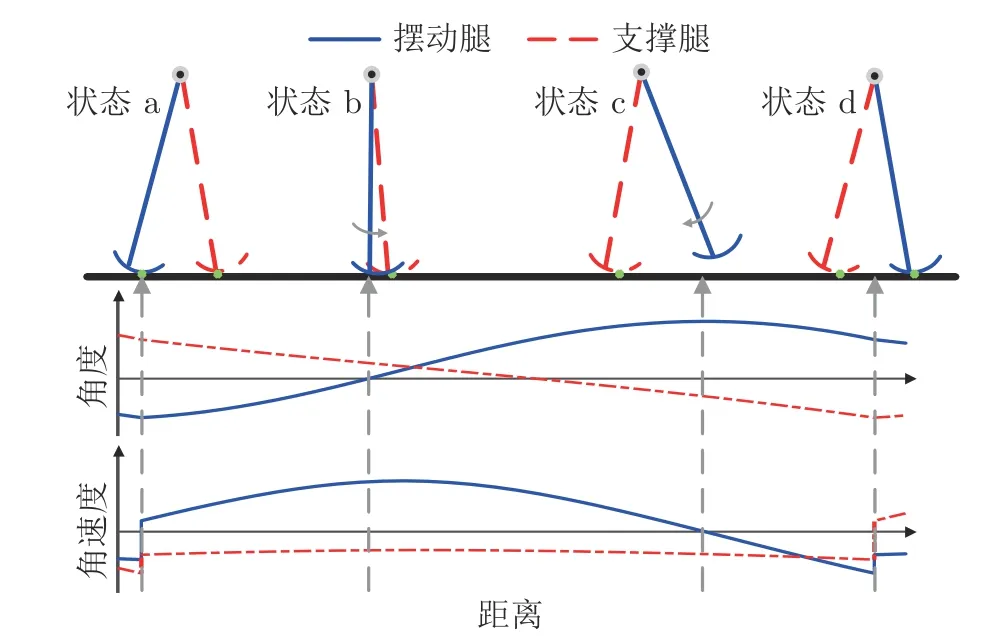
图2 被动步行过程Fig.2 Passive dynamic waking process

图2 中,状态a 至状态d 前为摆动阶段.此阶段,机器人支撑腿绕支撑点s做倒立摆运动,摆动腿离地并绕髋关节H做单摆运动,运动中忽略摆动腿的擦地现象,由Lagrange 法推导摆动阶段动力学方程:

其中,q为姿态向量 [θ1,θ2];M(q) 为 2×2 正定质量惯性矩阵;H() 为重力、离心力和哥氏力之和;μ(t)=[μst,μsw] 为控制力矩集合,μst、μsw分别为支撑腿踝关节与摆动腿髋关节处的电机力矩,当μ(t)=[0,0]时机器人处于被动步行状态.

状态d 时刻,机器人处于碰撞阶段.此阶段,机器人摆动腿在碰撞点cp 处与地面发生瞬时完全非弹性碰撞,碰撞前后发生突变,碰撞后,支撑腿与摆动腿间角色交换,满足:

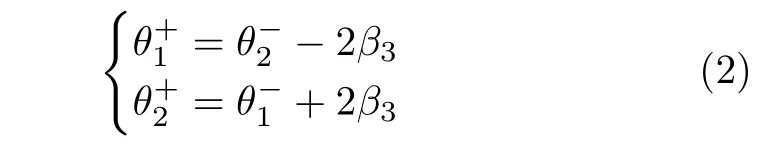
其中,β3为前向补偿角,“-”、“+”分别表示碰撞前瞬间和碰撞后瞬间.由于碰撞前后机器人关于碰撞点cp 处角动量守恒,碰撞后摆动腿关于髋关节H处角动量守恒,可得到碰撞阶段动力学方程:

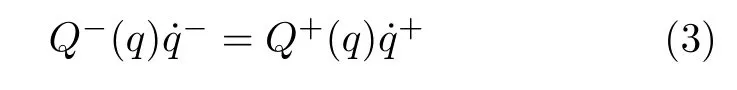
其中,Q-与Q+可由碰撞前后角动量守恒推导得到.联立式(1)～(3)完成机器人行走过程的混合动力学模型建立.

1.2 状态空间与动作空间

当机器人作为智能体时,其受控行走过程可用马尔科夫决策过程(Markov decision processes,MDP) 描述.通常,MDP 可记为四元数组(S,A,P,R).其中,S为智能体状态空间,A为智能体动作空间,P为状态转移函数,R为奖励函数.本文中,将机器人的状态空间定义为S=[x,φ],其中,x=为机器人起始状态,φ为斜坡坡度;令机器人动作空间为A=μsw,在机器人摆动摆动阶段中μsw恒定,可有效防止摆动腿在行走中抖动,保证步态的柔顺;由于μst空间范围更为广泛但对本文所选取的坡度范围下无明显的控制提升,因此令μst ≡0 即锁死踝关节,以减少训练耗时与控制能耗.因此在第t步时,机器人的行走过程可以描述为:状态st的机器人执行DRL 选择的动作at,根据P迁移至状态St+1,并通过R得到奖励值rt(st,at).

为减少分析参数,选取足地碰撞后瞬时时刻的机器人状态空间为庞加莱截面,则机器人状态的转换可利用庞加莱映射f实现,满足:

若存在状态x,满足x=f(x),称状态x为不动点,此时机器人步态即为稳定步态.结合MDP可知,以步态稳定为目标时,DRL 需选择动作使机器人快速到达不动点,以获得更高的奖励值.

2 深度确定性策略梯度算法

DDPG 是基于确定性策略梯度(Deterministic policy gradient,DPG)[34]改进的一种离线、无模型DRL 算法,适用于连续动作空间问题.采用DDPG 控制机器人行走,可以使机器人获得更准确的控制,加快步态的收敛速度.进一步利用PER 替代DDPG 原有的样本抽取机制,可提高样本利用率,改善DDPG 的学习能力.

2.1 算法结构

在DDPG 中,分别使用策略神经网络μ与价值神经网络Q表示DPG 与状态动作值函数,并组成AC 算法.其中,μ为Actor,当机器人状态为st时,μ选择动作at的过程为:

其中,θμ为μ的神经网络参数;Nt为动作扰动,由扰动函数N提供,用以在学习过程中探索环境.机器人在执行动作at后,结合返回的st+1与rt,将其结合st与at组成样本 [st,at,rt,st+1] 存入样本池.价值网络Q作为Critic,用以逼近状态动作值函数:

其中,θQ为Q的神经网络参数.

为稳定学习过程,DDPG 借鉴DQN 中的目标网络结构,构建目标策略网络μ′与目标价值网络Q′,并在目标网络中引入缓慢更新策略:

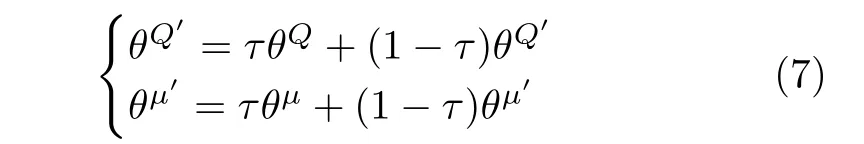
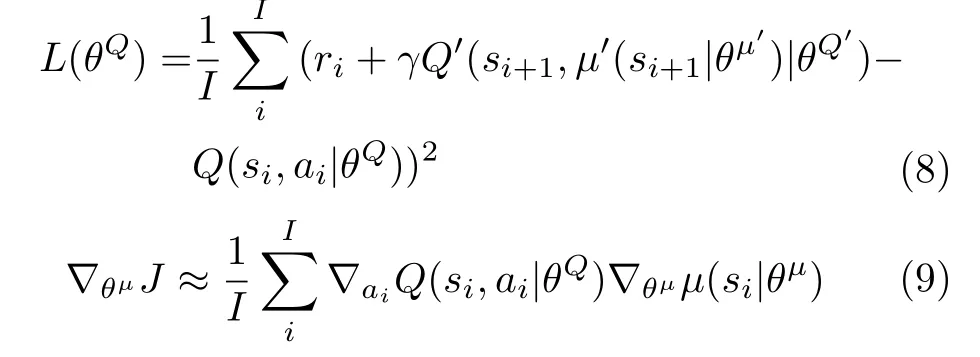
式中,γ为奖励折扣;Q′与μ′通过降低Q的变化幅度,抑制训练中Q和μ的网络震荡,达到稳定算法学习过程的目的,DDPG 中的神经网络训练过程如图3 所示.

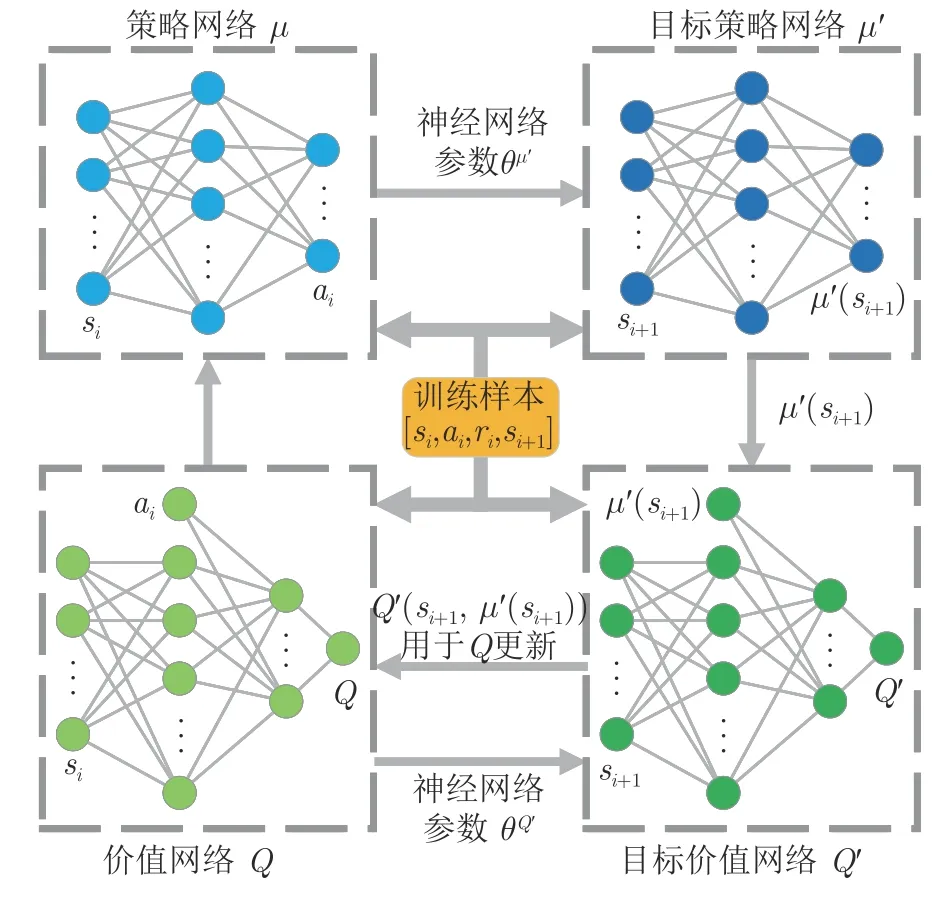
图3 DDPG 中神经网络训练过程Fig.3 The neural network training process in DDPG

2.2 优先经验回放策略的引入

虽然ER 能够打破样本间的相关性,满足DDPG中神经网络的离线训练要求,但ER 并不能判断其抽取样本的训练价值,导致DDPG 无法充分利用样本.为改善这一不足,采用PER 替代ER,以提升高价值样本利用率.

PER 使用时间差分(Temporal difference,TD)误差[35]表示样本的价值.令样本TD 误差绝对值越大时价值越高,则对于样本i,在DDPG 中的TD 误差为:

将样本池中的样本按TD 误差绝对值进行降序排列,建立样本的抽取优先级:

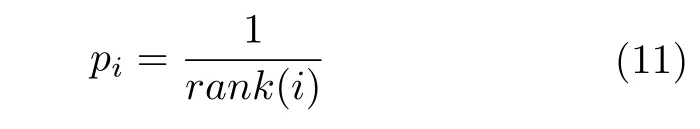
其中,rank(i) 为样本i排序后的队列序号,最高优先级pmax=1,即价值越高优先级越高.相比于直接使用TD 误差作为抽取依据,pi能够更好地抑制噪声样本的影响,此时样本i被抽取概率为:

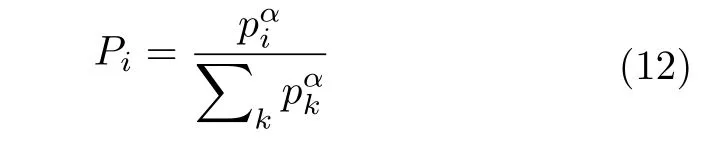
其中,k为样本总量;α∈[0,1] 可调节高价值样本在样本集中的比例,确保样本集内的样本多样性,α=0时即为随机抽取.同时,PER 中还使用重要性采样权重(Importance-sampling weights,IS)对频繁回放高价值样本造成的影响进行纠正,确保学习过程的稳定,样本i的IS 值可表示为:

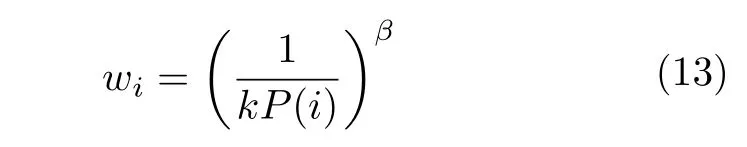
其中,β∈[0,1] 可控制纠正的程度,在价值网络Q的损失函数中加入IS 值,损失函数更新为:

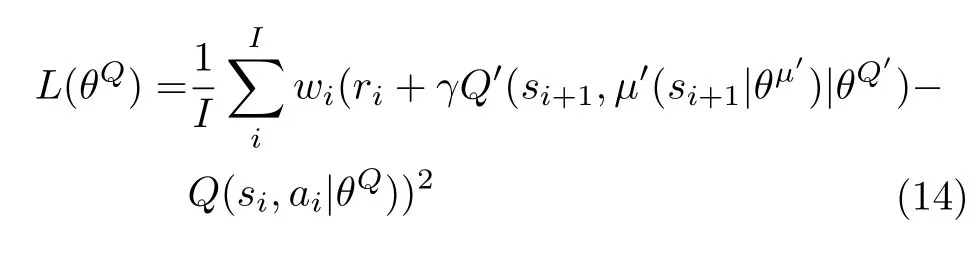
3 基于Ape-X DPG 的步态控制方法

基于PER 的DDPG 通过改变样本抽取机制进而改善算法学习能力,但其学习过程中训练与交互需顺序交替执行,限制了样本的采集速度,增加了学习时间.为此,本文在基于PER 的DDPG 的基础上引入DPER 结构,形成Ape-X DPG 算法,整体结构如图4 所示.

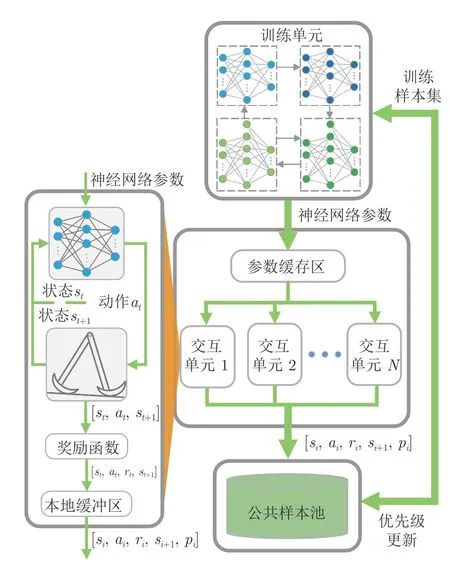
图4 Ape-X DPG 算法结构Fig.4 The structure of Ape-X DPG

3.1 Ape-X DPG 结构

如图4 所示,Ape-X DPG 主要由三部分组成:

1)交互单元.交互单元负责收集机器人的行走样本,可依据计算机性能部署多个,各单元间相互独立.交互单元由本地DDPG、本地样本池、机器人交互环境组成.其中,本地DDPG 控制机器人的行走,其从参数缓冲区中获得网络参数;本地样本池用于样本的缓存,当样本量超过存储上限时,计算样本初始优先级并送入公共样本池.

2)公共样本池.公共样本池负责存储交互中产生的所有样本,同时使用PER 为训练单元抽取训练样本集.为减少样本在排序与抽样时的计算消耗,公共样本池采用二叉树结构.

3)训练单元.训练单元利用样本集不断训练学习.训练单元本身不直接参与机器人的交互,但每次训练后,其会将训练后参数存入参数缓冲区中,并更新训练样本在公共样本池中的优先级.

为简化结构,本文将交互单元中的本地DDPG使用策略神经网络μ进行替代,称为本地Actor.简化后,样本的初始优先级均为pmax=1,此时使用PER 的公共样本池会优先抽取传入的新样本,使训练单元更重视最新样本的处理.

Ape-X DPG 通过上述三部分的并行执行,将DDPG 的交互与训练相分离,从而有效缩短学习时间.同时,多个交互单元的部署,极大地提升样本的收集速度,而交互单元间的相互独立,使得不同交互单元可以采用不同扰动函数N,增强了算法探索环境的能力,简化后的Ape-X DPG 过程如下所述:

3.2 双足机器人交互过程

为使Ape-X DPG 习得高效的步态控制策略,限定一次Episode 中最大行走步数为10 步.同时,为模拟机器人多样的不稳定步态,随机选择机器人的初始状态s1,交互单元n中1 次Episode 的过程如图5 所示.

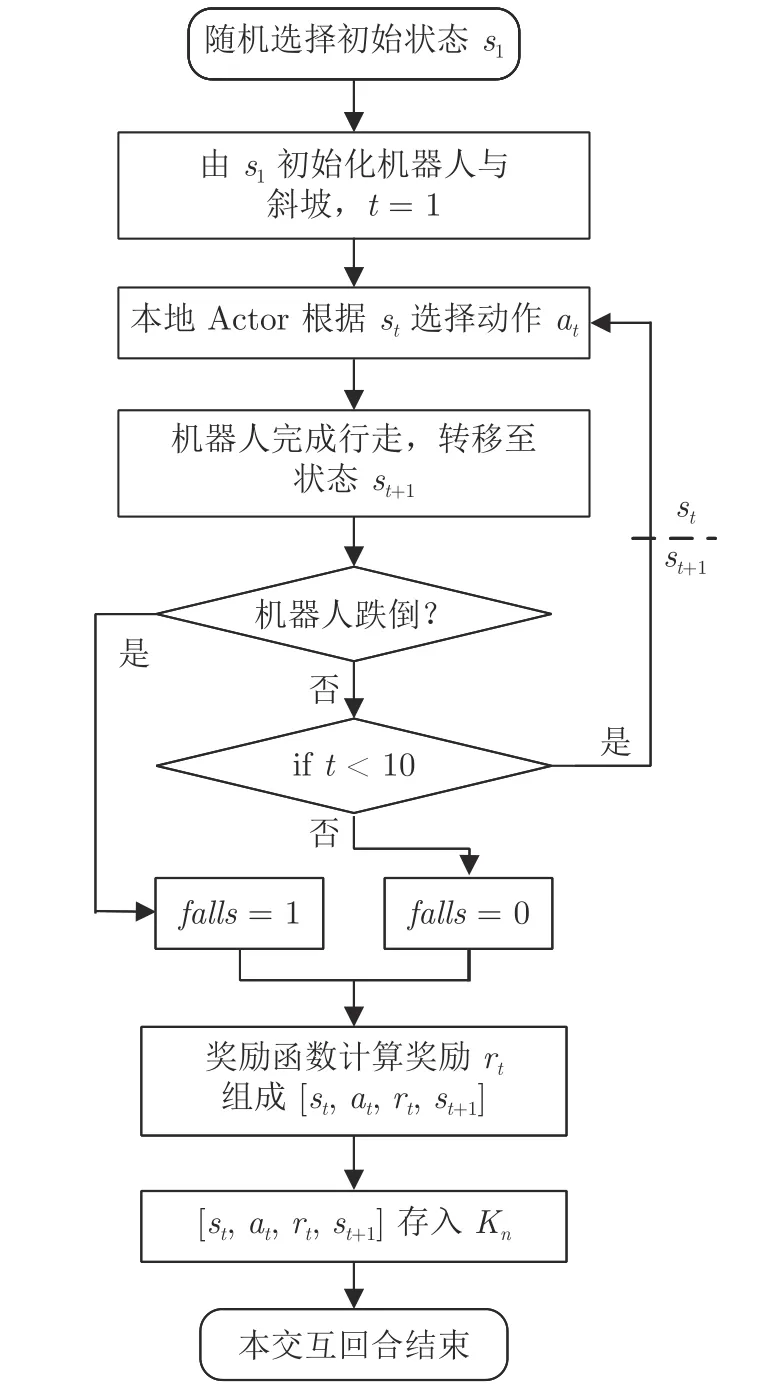
图5 交互单元n 中Episode 过程Fig.5 Episode process in interaction unit n

图5 中,falls用于标识机器人在本次Episode 的完成状态,若在Episode 中机器人跌倒,则将Episode 中的各步标记为falls=1;若机器人完成10 步行走,则各步标记为falls=0.

3.3 奖励函数设计

不动点能够表征机器人稳定行走时的状态,常被用于奖励函数的设计.但由于不动点求解困难且随φ的变化而变化,因此其不适合较大斜坡范围下的奖励函数设计.当机器人状态处于不动点时,机器人步态单一且无需外力矩作用,因此奖励函数可设计为:

其中,Δ=4‖xt+1－xt‖2表示机器人在庞加莱截面上的步态变化,xt、xt+1分别从样本中的st、st+1获得;ar=25|at|为缩放后的动作at.当falls=1 时,机器人获得奖励值-1.当falls=0 时,奖励函数利用Δ与αr替代不动点评价机器人步态稳定程度,奖励函数空间如图6 所示:

图6 falls=0 时的奖励函数空间Fig.6 Landscape of the reward function when falls=0

图6 中,奖励函数空间整体呈现单调变化趋势,当Δ与ar均趋近0 时将步态视为稳定,给予机器人高奖励值.在奖励函数中引入动作at,可以引导Ape-X DPG 选择较小的动作调节机器人步态,提高机器人能效,同时减小对稳定步态的扰动.

4 仿真实验

4.1 仿真实现细节

本文通过Python 与Matlab 的联合仿真对Ape-X DPG 的学习与控制能力进行验证.其中,Python 负责Ape-X DPG 的实现;Matlab 负责机器人的动力学仿真;Python 与Matlab 间通过Matlab Engine 进行通信.为 保证结果的一致性,图像均使用Matlab 进行绘制.

在Matlab 中,机器人物理参数设置如表1 所示.为更好地检验算法控制能力,仿真实验中机器人采用稳定性较差的对称圆弧足[36],此时β3=0、碰撞后θ1=－θ2.基于机器人的步态运动特征,限定初始时的状态空间S1范围:θ1∈[0.02,0.6]、∈[－2,－0.08]、∈[0,6] 、φ∈[0.04,0.15],并限定动作空间A中的usw∈[－0.3,0.3].

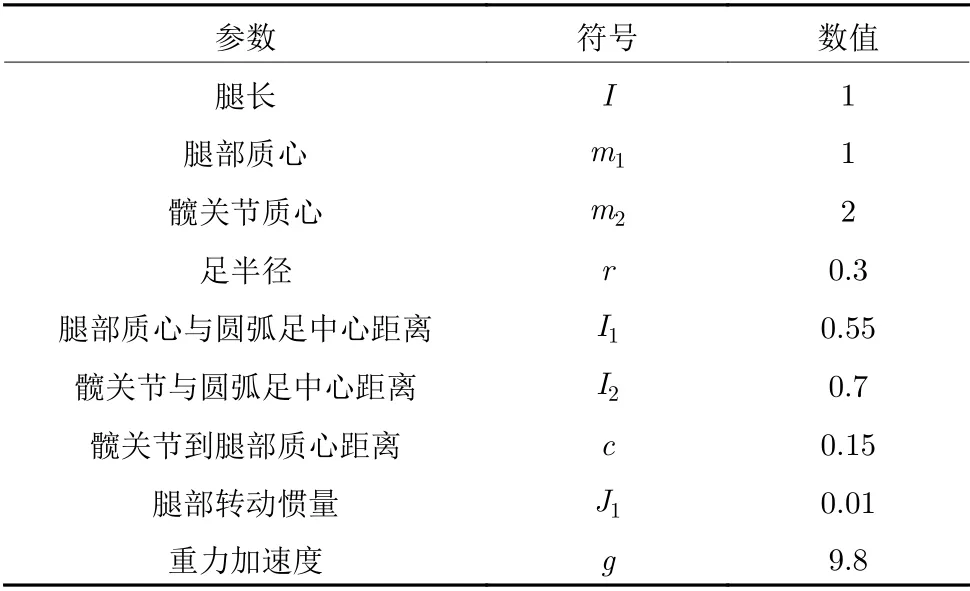
表1 机器人符号及无量纲参数Table 1 Symbols and dimensionless default values of biped parameters

在Python 中,采用Tensorflow[37]实现的Ape-X DPG,交互单元、公共样本池分配于不同CPU核心中,训练单元则分配至GPU 中.训练单元中,Q和μ使用全链接神经网络,均有4 个隐藏层,各层单元数分别为100、300、200、50,使用ReLU 激活函数.输入层单元数由状态空间S决定,且Q在第3 隐藏层中接收对应动作a.对于输出层激活函数,μ使用tanh 激活函数,而Q不使用激活函数.在训练过程中,μ和Q的学习率分别设置为 10-4、10-3,使用Adam 算法[38]更新.μ′和Q′更新参数τ为 10-4.

公共样本池存储上限为 5×105,PER 中参数设置分别为α=0.7、β=0.4.交互单元中,本地Actor 结构与μ相同,本地样本池存储上限为 103.

4.2 学习过程

由于交互单元数量与扰动函数N设置均影响着算法性能,本文通过3 组不同交互单元数量的Ape-X DPG 和1 组基于PER 的DDPG 进行仿真实验,对比算法的学习能力与收敛速度.在学习开始后,当公共样本池样本总数到达 2.5×105时启动训练单元,当各采集单元均完成20 000 次Episode 时结束学习.各组仿真实验中N分配与训练单元启动后的学习耗时如表2 所示,表中0,1,2 表示该组算法中使用对应N的交互单元数.训练单元启动后各算法奖励曲线如图7 所示.

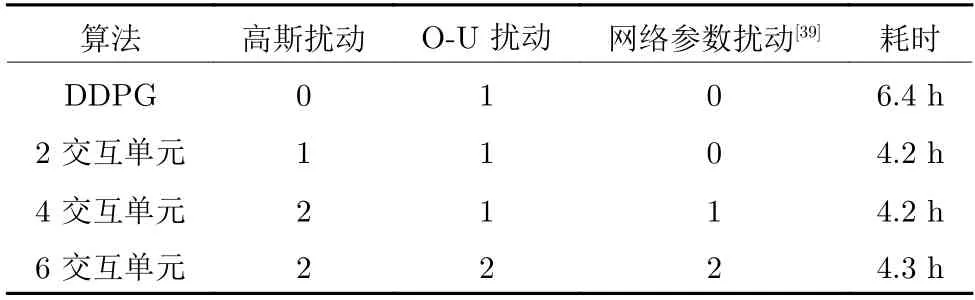
表2 扰动函数N 分配与学习耗时Table 2 Noise function N settings and learning time

图7 中,曲线表示各组算法中交互单元对应Episode 奖励的平均值.其中,点线为DDPG 的奖励值,可以看出其学习速度缓慢且学习过程存在明显的震荡,虽然与2 交互单元Ape-X DPG 最终的平均奖励值相差不大,但Ape-X DPG 的收敛更早且过程也更加稳定.同时,由于Ape-X DPG 中交互与训练并行运行,因此在相同条件下,Ape-X DPG的学习耗时显著低于DDPG.对于三组Ape-X DPG,其在收敛后的平均奖励值大小与交互单元数量成正比,且由于各交互单元独立运行,使得三组算法在执行固定交互次数时学习整体耗时差异较小.

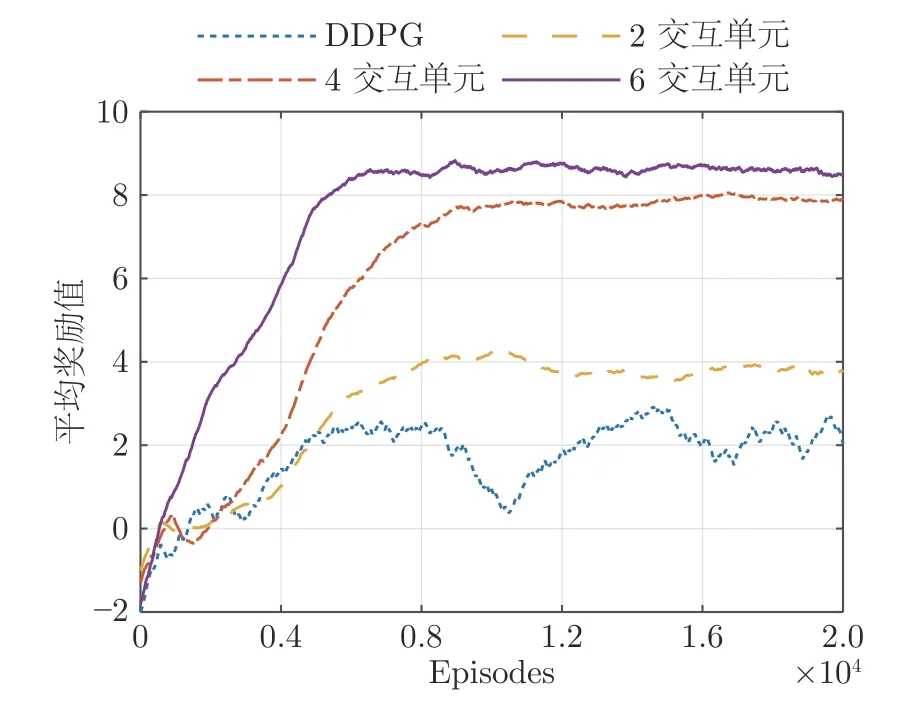
图7 平均奖励值曲线Fig.7 The curves of the average reward

4.3 步态控制分析

为测试Ape-X DPG 的步态控制能力,本文选择能量成型控制作为对比控制算法.当机器人在斜坡上被动行走时,摆动阶段中重力所做功转化为系统动能,若碰撞阶段中这部分能量被精确消耗,则机器人能量变化形成平衡,可实现稳定行走;若能量无法被精确消耗,则会导致机器人行走的不稳定.能量成型控制利用上述过程,将机器人不动点处能量总值Etarget作为参考,通过μt=[μst,μsw] 的作用,使机器人不稳定初始能量Et快速收敛至Etarget,进而实现步态的调整,有控制率:

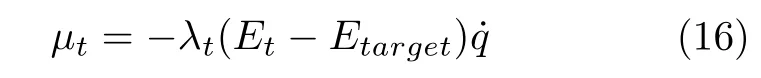
其中,λt为自适应系数,具体为:

其中,ξ为可调阻尼系数,υt-1为机器人第t-1 步时步态周期变化,表示为:

其中,Tt-1为机器人第t-1 步的行走时间.λt能够依据步态不稳定程度对力矩大小进行调整,加快步态收敛速度.

不失一般性,从初始状态空间中随机抽取 2 000组作为测试集.能量成型控制选取参数ξ=0.8,初始λt为λ1=0.01,对于初始阶段所需的Tt-1等,使用稳定步态行走时间补充.DDPG 与Ape-X DPG使用上节训练所得参数,在机器人行走15 步时检测步态是否稳定,各算法稳定行走次数如图8 所示.

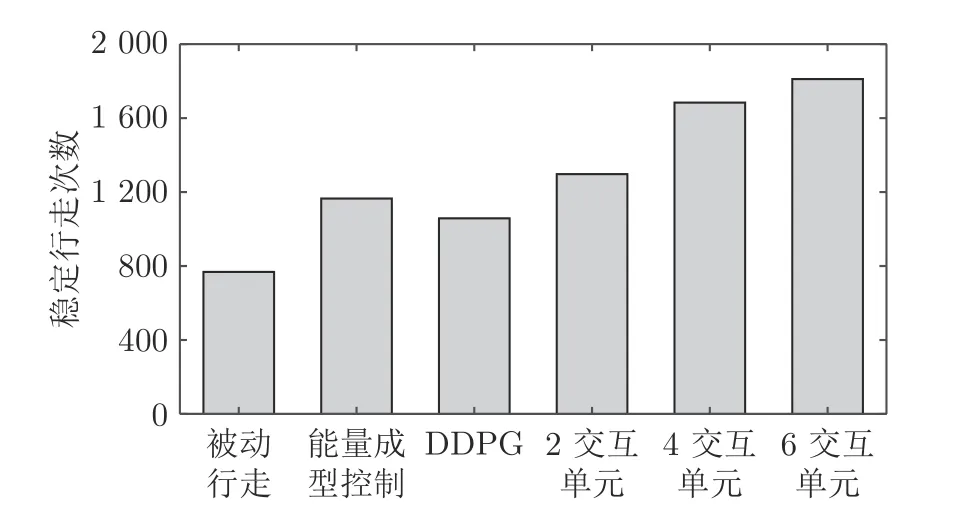
图8 测试集稳定行走次数Fig.8 Stable walking times in test

图8 中,能量成型控制同DDPG、2 交互单元Ape-X DPG 的稳定行走次数接近,均高于被动行走.6 交互单元Ape-X DPG 控制能力优于其他算法,实现最高的1 811 次稳定行走,因此本文后续采用6 交互单元Ape-X DPG 进行分析.从测试集中选择2 组初始状态,如表3 所示.

表3 机器人初始状态Table 3 The initial states of the biped

图9 为以初始状态a、b 行走的机器人前进方向左侧腿相空间示意图,初始状态a 时,两种算法均可阻止机器人跌倒,使机器人步态收敛至稳定状态,并最终形成一致的运动轨迹.相比于能量成型控制,Ape-X DPG 的控制过程更快,仅通过两步的调整便使机器人步态趋近于稳定;在初始状态b 时,能量成型控制失效,无法抑制机器人的最终摔倒,而Ape-X DPG 依然可以完成机器人不稳定步态的快速恢复.

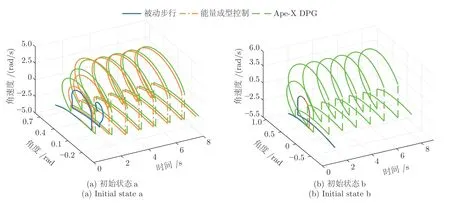
图9 机器人左腿相空间图Fig.9 The phase plane of the right leg

图10 为初始状态b 时两种算法的控制过程,由于机器人初始状态的能量与不动点的能量接近,使得能量成型控制效果微弱,经过3 步调整,仍然无法抑制机器人跌倒.而在Ape-X DPG 作用下,机器人第一步时达到最高2.842 rad/s,高于能量成型控制时的2.277 rad/s,较大的增大了机器人步幅、延长了第一步行走时间,同时控制力矩的输入增加机器人系统机械能,使碰撞后、绝对值增大,机器人状态则转移至s2=[0.39896,－1.60110,1.38857,0.121].对比能量成型控制s2=[0.25749,－1.82706,－0.76343,0.121]可知,Ape-X DPG 在第一步时便使机器人步态向不动点x=[0.47213,－1.71598,3.33070]靠近.此后,Ape-X DPG 作用力矩逐步减小并收束为0,最终机器人步态恢复稳定,主动控制行走转为被动行走,两种控制方法控制下的机器人棍状图如图11 所示.

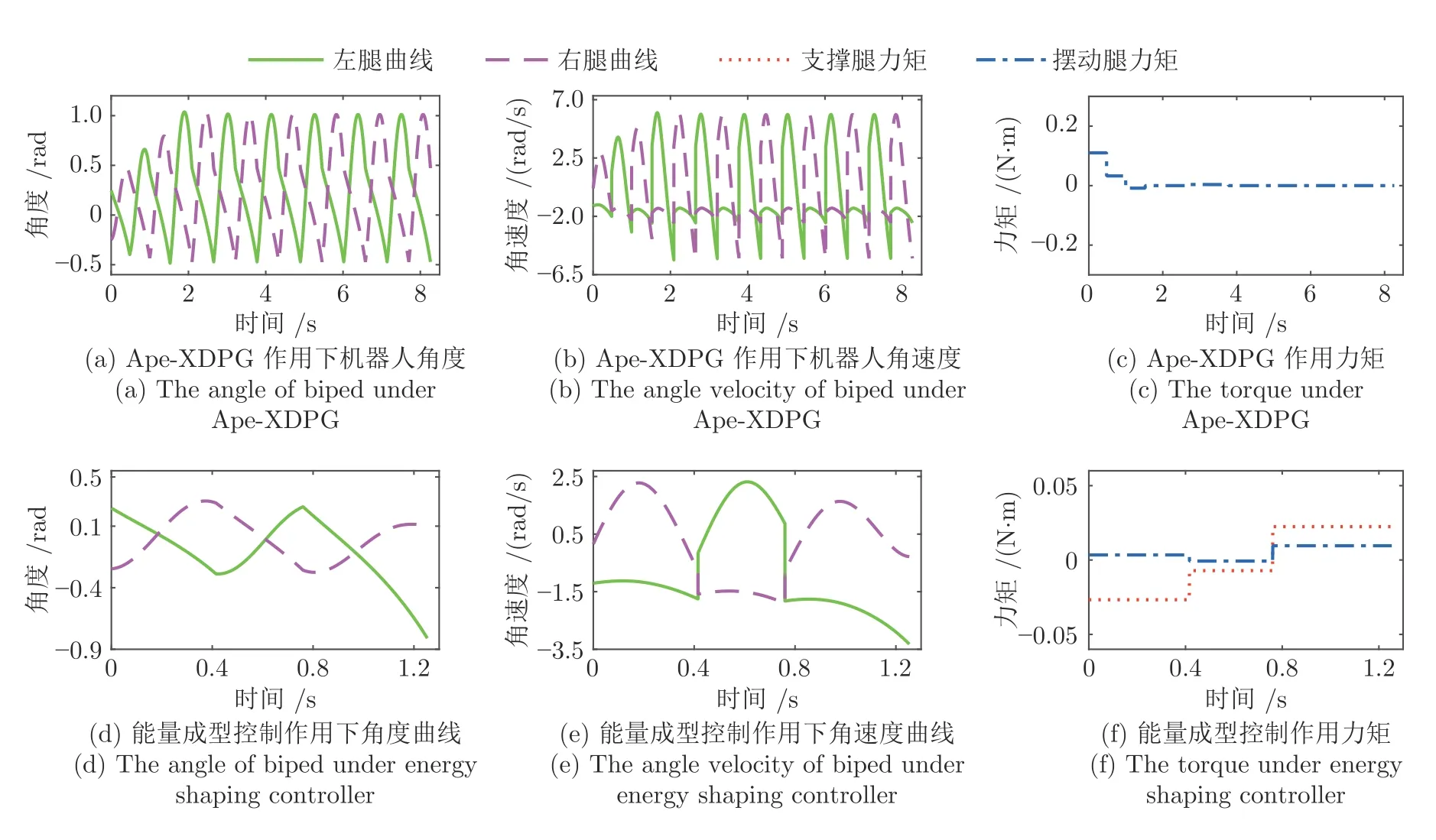
图10 初始状态b 时机器人行走状态Fig.10 Biped walking state in initial state b

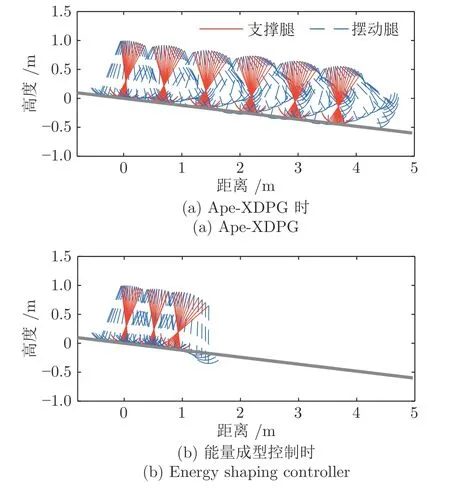
图11 机器人行走过程棍状图Fig.11 The gait diagrams of the biped

通过棍状图可直观看出,在Ape-X DPG 控制下机器人前3 步中摆动腿摆动幅度逐步增大,并在4 步时开始稳定行走,而在使用能量成型控制时,机器人在第3 步时未能将摆动腿摆至地面上方,进而引发了跌倒.

进一步的,使用Solidworks 建立机器人物理模型,并基于Matlab 中的Simscape Multibody 进行物理仿真,机器人模型参数同表1,模型如图12 所示.

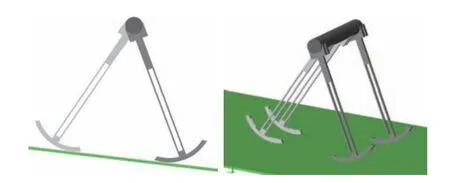
图12 机器人物理模型示意图Fig.12 Sketch of the biped physical model

在机器人模型中,外侧腿为灰色,内侧腿为白色,并定义外侧腿为物理仿真时的起始支撑腿.为解决摆动阶段中摆动腿的擦地现象,将摆动腿前摆时的足部碰撞参数置为0,回摆时恢复碰撞参数,以实现足地碰撞.在上述条件下,初始状态b 的机器人在Ape-X DPG 控制下的前10 步行走过程如图13所示.

图13 机器人物理仿真Fig.13 Robot physics simulation

图13 (a)为机器人前4 步的行走过程,在图13 (c)中0 s 时的角速度阶跃为机器人从空中释放后落地瞬间造成的速度突变.从图13 (b)、13 (c) 与图10 (a)、10 (b)对比可以看出,物理仿真与数值仿真在角度变化上大致相同,但在角速度变化中存在差异,主要原因为物理仿真下机器人碰撞阶段无法实现完全非弹性碰撞.因碰撞阶段的不同,导致图13 (d)中Ape-X DPG 作用力矩无法数值仿真时一样收敛至0,但依然可以阻止机器人的跌倒,并使机器人在状态x=[0.46,－1.73,1.81] 附近进行行走.

4.4 全局稳定性分析

为进一步刻画Ape-X DPG 的控制能力,采用胞映射法分别获得被动步行、能量成型控制、Ape-X DPG 三种情况下的机器人步态收敛域(Basion of attraction,BOA).BOA 是机器人可稳定行走的初始状态集合,其范围越大时机器人步行稳定性越高[40].为检测算法在不同坡度下的控制能力,将φ=[0.04,0.15]以0.01 等间隔划分,获得12 组步行环境.进一步将初始状态S1中的x=[θ1,,] 划分为 6.4×104个胞.

三种情况下机器人稳定行走胞数如图14 所示,在选取的12 组坡度中,Ape-X DPG 控制下BOA稳定行走胞数均远高于被动步行与能量成型控制,并在φ=0.1 时获得最大胞数为55 649,此时BOA可覆盖胞空间的86.95 %,而此时被动步行与能量成型控制胞数分别为27 371、38 692,覆盖胞空间为42.76 %、58.89 %.取φ=0.1 时的BOA 进行绘制,如图15 所示,其中绿色部分为BOA 区域,蓝色为跌倒步态区域.图15 (c)中,Ape-X DPG 的BOA范围显著增加,进一步证明Ape-X DPG 可有效提高机器人步行稳定性.

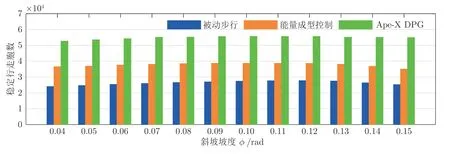
图14 稳定行走胞数Fig.14 The number of the state walking

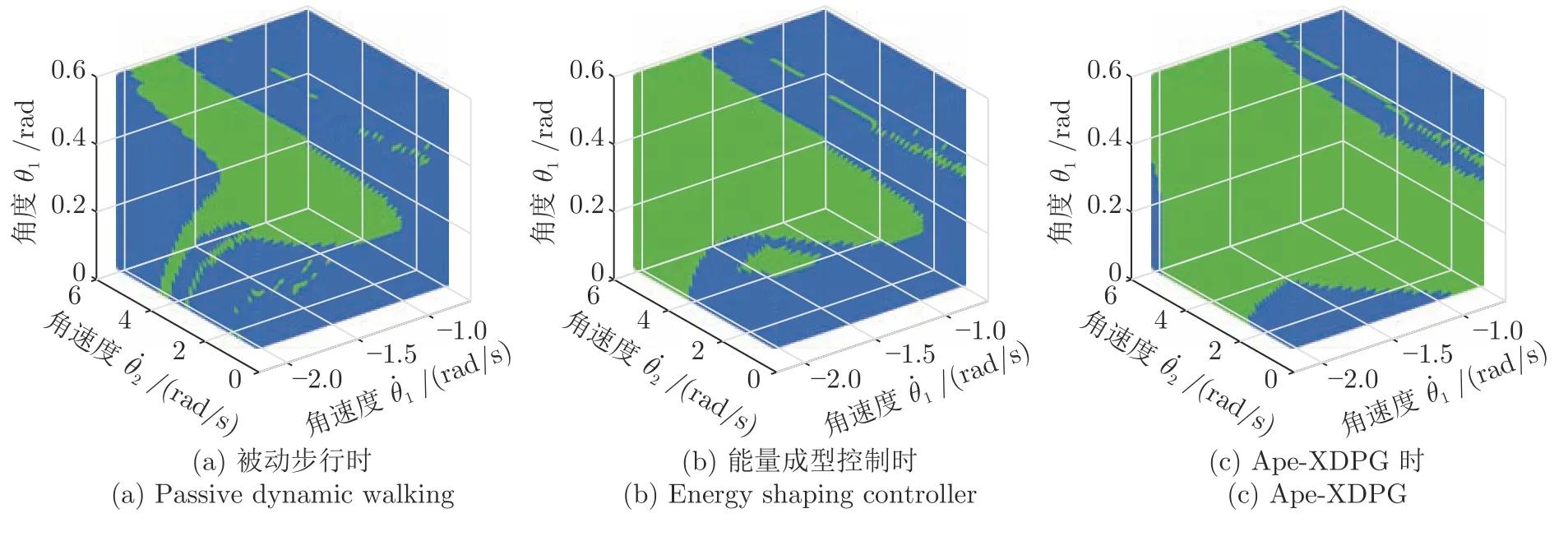
图15 φ=0.1 时机器人步态收敛域Fig.15 The biped BOA whenφ=0.1

5 总结

本文提出了一种稳定、高效的准被动双足机器人斜坡步态控制方法,实现了 [0.04,0.15] rad 斜坡范围内的机器人步态稳定控制.在DDPG 的基础上,融合PER 机制与DPER 结构建立了Ape-X DPG分布式学习算法,以加快样本采集速度、提高样本利用率、缩短学习时间.将机器人视为智能体,结合Ape-X DPG 分布式的交互过程,基于机器人行走特性的准确描述,设计了Episode 过程与奖励函数.经学习后,Ape-X DPG 能够控制机器人在 2 000组测试中完成1 811 次稳定行走,并在φ=0.1 时使机器人BOA 覆盖86.95 %的胞空间.相较于能量成型控制,Ape-X DPG 能够更有效地调节准被动双足机器人不稳定步态、抑制跌倒,达到提高准被动双足机器人斜坡步行稳定性的目标.